具有外扰的不确定Lurie系统的同步控制

张 伟,谢 芝,毛北行

(郑州航空工业管理学院数理系,河南 郑州 450015)

具有外扰的不确定Lurie系统的同步控制

张 伟*,谢 芝,毛北行

(郑州航空工业管理学院数理系,河南 郑州 450015)

利用修正函数投影同步方法研究了具有外扰的不确定Lurie混沌系统的同步问题,基于Lyapunov稳定性理论给出了系统同步的充分条件,最后数值算例,表明了该方法的有效性.

混沌系统;Lurie系统;投影同步

近年来,混沌同步方面的研究取得了巨大的进展[1-5],文献[6]研究了一类混沌系统的修正函数投影同步问题,文献[7]研究了耦合混沌系统的自适应修正函数投影同步问题,而Lurie系统的研究引起了国内外学者的广泛兴趣[8-10].本文研究具有外扰的不确定Lurie混沌系统的修正函数投影同步问题,基于Lyapunov稳定性理论给出系统函数投影同步的充分条件,最后数值算例,表明该方法的有效性.

1 问题描述和主要结果

首先考虑如下Lurie混沌系统:

其中x,y∈Rn;g(σ(x)),h(σ(y),x)是光滑的非线性函数.

定义1 若存在函数矩阵M(t)=diag[m1(t),m2(t),...,mn(t)]使得

则称系统(1)和(2)获得修正函数投影同步,其中mi(t)为对应状态变量的比例因子.

以系统(1)为驱动系统,构造如下相应系统:

假设1 ‖g(σ(x))-g(Mσ(y))‖≤L‖σ(x)-Mσ(y)‖,L为Lipschitz常数,系统误差e(t)=x(t)-My(t)=[x1-m1(t)y1,x2-m2(t)y2,...,xn-mn(t)yn].

则误差系统为

定理1 选取控制律u=ηe,η为适当维数的常数矩阵,若满足-K+LC-η＜0,则系统(1)与(3)是修正函数投影同步的.

证构造Lyapunov函数,由假设1很容易得到

以下考虑具有外扰的不确定Lurie混沌系统:

以系统(4)为驱动系统,构造如下相应系统:

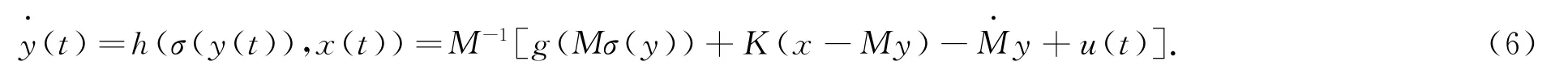
假设2≤β,其中α,β为大于零的常量.系统误差e(t)=x(t)-My(t)=

则误差系统为

K为耦合反馈系数.

定理2 选取控制律,以及自适应律下,若满足LC-K＜0,则系统(4)与(6)是修正函数投影同步的.

证构造Lyapunov函数V(x(t))=

2 数值算例

耦合系统为:

系统(1),(2)的初值分别为:x(0)=(4,4,4,4);y(0)=(4,4,4,4),反馈系数k2=0.5,

外扰取为均值为0,方差为1的随机扰动,控制器取为:

3 结论

利用修正函数投影同步方法研究了具有外扰的不确定Lurie混沌系统的同步问题,利用Lyapunov函数方法给出了证明并得到了系统完全同步的充分条件,最后给出了数值例子,表明了该方法的有效性.

[1]Pecora L M,Carroll T L.Synchronization in Chaotic Systems[J].Phys Rev Lett(S0031-9007),1990,64(8):821-824.

[2]Pecora L M,Carroll T L.Driving Systems with Chaotic Signals[J].Phys Rev A(S0277-786X),1991,44(4):2374-2383.

[3]Yoo W J,Ji D H,Won S C.Synchronization of two different non-autonomous chaotic systems using fuzzy disturbance observer[J].Physics Letters A,2009,374(11):1354-1361.

[4]Fallahi K,Leung H A.Chaos secure communication scheme based on multiplication modulation[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(2):368-383.

[5]吕翎,李纲,张檬,等.全局耦合网络的参数辨识与时空混沌同步[J].物理学报,2011,60(9):5051-5056.

[6]李建芬,李农.一类混沌系统的修正函数投影同步[J].物理学报,2011,60(8):5071-5077.

[7]方洁,胡智宏,江泳.耦合混沌系统自适应修正函数投影同步[J].信息与控制,2013,42(1):39-45.

[8]何汉林,涂建军,熊萍.一类Lurie混沌系统的全局渐近同步[J].华中科技大学学报,2010,38(2):38-40.

[9]毛北行,王东晓,卜春霞.Lurie混沌系统的脉冲控制同步[J].华中师范大学学报:自然科学版,2012,46(3):297-299.

[10]毛北行,程春蕊,卜春霞.Lurie混沌系统的修正函数投影同步[J].数学杂志,2013,33(4):717-710.

Chaos synchronization control of uncertain Lurie chaotic system with external perturbation

ZHANG Wei,XIE Zhi,MAO Beixing
(Department of Mathematics and Physics,Zhengzhou Institute of Aeronautical Industry Management,Zhengzhou 450015,China)

The problem of synchronization of uncertain Lurie chaotic system with external perturbation is studied in the paper.We get the sufficient condition of chaos synchronization for Lurie chaotic systems by Lyapunov stability theory.Numerical example of chaotic system verify the effectiveness of the proposed method.

chaotic systems;Lurie systems;projective synchronization

O482.4

:A

:1671-9476(2015)05-0006-03

10.13450/j.cnki j.zknu.2015.05.002

2015-03-17;

:2015-04-20

国家自然科学基金(No.51072184);国家自然科学基金数学天元基金(No.11226337);河南省科技厅基础与前沿技术研究计划项目(No.122300410390);河南省高等学校重点科研项目(No.15B110011)

张伟(1978-),男,山东菏泽人,讲师,硕士,主要从事计算数学和数学建模研究.