HTPB推进剂力学性能散布与确定变量相关性研究
张 晓,郑 坚,彭 威,顾志旭
(军械工程学院,石家庄 050003)
HTPB推进剂力学性能散布与确定变量相关性研究
张 晓,郑 坚,彭 威,顾志旭
(军械工程学院,石家庄 050003)
针对复合固体推进剂力学性能存在散布的问题,通过方差分析试验,研究了松弛模量和泊松比的散布与确定变量之间的相关性。建立了力学性能散布的方差分析模型,分析了散布的变化规律,并对导致变化的原因进行了讨论。结果表明,松弛模量的散布受温度和载荷作用时间影响显著;泊松比的散布在不同的应变阶段差异较大,结构损伤的不确定性是导致泊松比散布变大的主要原因;玻璃化转变及结构失效会引起力学性能的很大散布。
HTPB推进剂;方差分析;力学性能散布;结构损伤;松弛模量;泊松比
0 引言
由于受到生产工艺、环境因素等的影响,固体推进剂力学性能参数客观上存在散布[1]。HTPB推进剂在生产和使用过程中,受温度载荷、冲击载荷以及加速度载荷作用明显[2],载荷作用下,药柱应力场、应变场分布对部分材料参数(初始模量、泊松比等)具有较高的敏感度[3],力学性能参数的很小偏差,将引起药柱危险部位应力应变的明显变化,因此,力学性能散布将直接影响火箭发动机的工作稳定性,考虑推进剂力学性能参数的散布,分析其与确定变量之间的相关性,有助于改善发动机性能,提高结构完整性评估的准确性。
力学性能的散布是对力学性能确定程度的定量表征,反映某一确定条件下力学性能的分散程度。张海联等[1,4]在进行药柱结构完整性分析时,运用随机有限元法,考虑了松弛模量和泊松比的随机性;王君祺等[5]假设泊松比分布为截断型高斯分布;刘冬青等[6]采用Monte-Carlo和响应面法研究了推进剂热膨胀系数和初始泊松比的不确定性对药柱结构分析的影响,以上均是将药柱力学性能参数进行人为的随机离散,对于参数的实际散布大小及变化规律考虑较少。施陈波等[7]研究了推力测量不确定度的主要来源及变化规律;胡松启等[8]推导了热损失率的不确定度方程,得到了影响热损失率测量散布的主要因素;Lal A等[9]对推进剂余量预测的不确定度进行了评估;Evans J A[10]曾指出,推进剂燃烧速率的散布可能与温度有明显的相关性,但未做进一步的深入研究。
本文通过方差分析试验,得到了HTPB推进剂松弛模量和泊松比散布的变化规律,找出了不确定性的力学性能参数分布与确定变量(温度、加载时间、应变)之间的相关性,并对可能的原因进行了讨论,提出了药柱使用过程中力学性能的许用散布,以期为配方、工艺的优化及结构完整性的准确评估提供参考。
1 数学模型
1.1 松弛模量散布的双因素方差分析模型
应力松弛模量按式(1)计算:
(1)
式中E(t)为τ时刻的应力松弛模量,MPa;F(t)为t时刻的松弛力,N;ε0为初始恒定应变;A0为试件初始横截面积,mm2。
松弛模量的散布用样本均方差表示为
(2)

为了判定温度和载荷作用时间的变化对松弛模量散布是否具有显著影响,以样本均方差值为对象,进行无交互作用的双因素方差分析,则偏差平方和为
(3)
(4)
(5)
(6)

由式(3)~式(6)可得
SSA=SST+SSt+SSE
(7)
式(7)表明,松弛模量散布的总差异可分解为温度和加载时间的不同所引起的差异和由随机因素引起的差异之和。
选取统计量:
(8)
(9)
取定显著性水平α,比较统计量的临界值Fα与实际观察值FT、Ft,若FT>Fα,则温度对散布有显著影响;若Ft>Fα,则载荷作用时间对散布有显著影响。
1.2 泊松比散布的单因素方差分析模型
泊松比按式(10)计算:
(10)
式中ν(ε)为泊松比;εy(ε)为横向应变;ε为拉伸应变。
泊松比的散布用样本均方差表示为
(11)
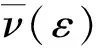
为了判定应变对泊松比散布有无显著影响,对泊松比的样本均方差进行单因素方差分析,偏差平方和为
(12)
(13)
(14)

由式(12)~式(14)可得
SSA=SSε+SSE
(15)
式(15)表明,泊松比散布的总差异可分解为应变的不同所产生的差异和由随机因素引起的差异之和。
选取统计量:
(16)
取定显著性水平α,比较统计量的临界值Fα与实际观察值Fε,若Fε>Fα,则应变对泊松比的散布有显著影响。
2 试验
试验材料:将某型HTPB推进剂材料加工成标准哑铃型,标距70 mm,截面10 mm×10 mm,试件受拉部分表面涂有黑白分明的目标,如图1所示。目标具有2条与试件纵向平行的黑白分界线,分界线应平整、光滑。
试验设备:微机控制五头电子式万能试验机;高低温试验箱;光学位移跟踪器;数字存储示波器;函数记录仪。
试验主要内容:
(1)在70、50、20、0、-20、-40、-50、-60 ℃下,以500 mm/min的拉伸速率,分别将8组试件(每组10个)单向等速拉伸至恒定应变5%,进行应力松弛试验,记录松弛时间2、4、8、20、40、80、200、600、1 000 s时的松弛力值;
(2)在环境温度下,以2 mm/min的拉伸速率,分别将5组试件(每组10个)进行单向等速拉伸,记录断裂前4个应变点处的变形值。
试验的单向拉伸由微机控制五头电子式万能试验机进行,高低温试验箱控制试验温度,各温度下试件保温时间均为1 h,泊松比的测试与2 mm/min单向等速拉伸同时进行,被测试件X(纵向)和Y(横向)2个方向的变形分别由万能试验机和光学位移跟踪器测得。位移跟踪器测量变形时捕捉的目标为受拉部分表面的黑白分界线。
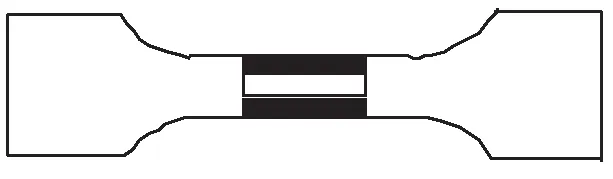
图1 试件示意图
3 结果与讨论
3.1 松弛模量散布与确定变量相关性
采用样本均方差S表示松弛模量测量结果的散布,如表1所示。

表1 松弛模量测量结果散布
由表1可知,松弛模量散布随温度的升高和松弛时间的增加呈现降低趋势,为了进一步判定温度和松弛时间是否对测量结果的散布有显著影响,对样本均方差进行双因素方差分析(取α=0.01),方差分析表如表2所示。由表2可知,F的观测值Ft=10.014>2.99,FT=348.28>3.51。所以,时间和温度对结果散布的影响均比较显著,说明松弛模量的散布与温度和载荷作用时间具有明显的相关性,三者关系的拟合方程见表3。
表2给出了时间、温度和随机因素三者产生的偏差平方和。结果表明,温度引起的散布大小的差异大于时间和随机因素引起的差异,而由时间产生的差异相对较小,接近于随机波动带来的差异,根据表1中数据随温度和时间的变化幅度可得到相同的结论,同时由表1可看出,松弛模量散布大小随时间的增加缓慢降低,且当达到较长时间后,基本趋于稳定;另一方面,当温度为-60 ℃时,松弛模量散布很大,力学性能波动明显,而当温度高于-60 ℃,尤其是高于-40 ℃时,散布大幅度降低,此后随着温度的升高缓慢减小,由于-60 ℃接近于材料的玻璃化转变温度,因此可认为,当温度下降至玻璃化转变温度附近时,推进剂力学性能将很难预测。

表2 双因素方差分析

表3 松弛模量散布与温度和时间关系的拟合方程
3.2 泊松比散布与确定变量相关性
泊松比测量结果的样本均方差见表4。
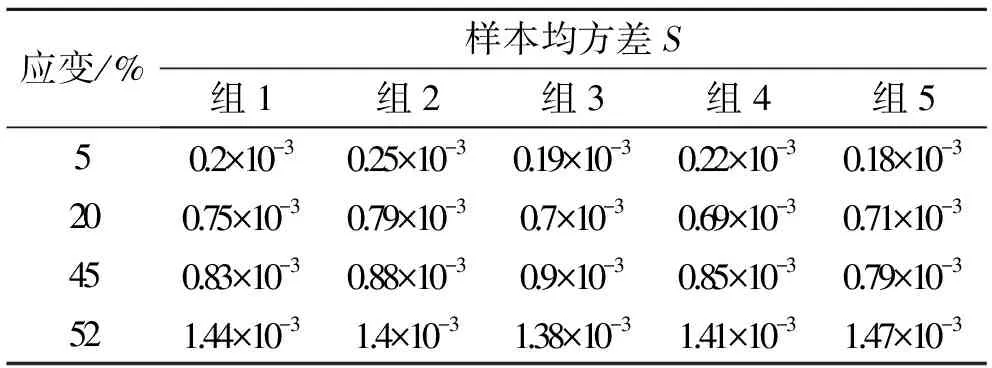
表4 泊松比测量结果散布
为了判定应变是否对泊松比测量结果的散布有显著影响,对样本均方差进行单因素方差分析(取α=0.01),方差分析表如表5所示。

表5 单因素方差分析表
由表5可知,Fε=885.6>5.29。所以,应变对泊松比结果散布的影响显著,表明泊松比散布与应变量具有明显的相关性。
根据文献[11],将2 mm/min单向等速拉伸应力应变曲线分为4个阶段:线弹性区(AB段)、脱湿发生区(BC段)、应力平台区(CD段)及趋于断裂区(DE段),见图2。
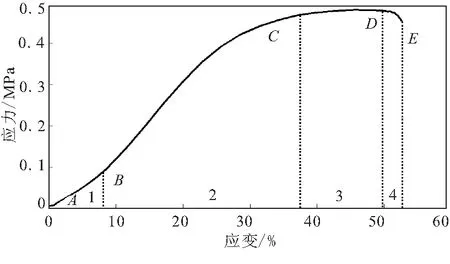
图2 2 mm/min单向等速拉伸σ-ε试验曲线
泊松比测量的记录点分别取自试件变形的不同阶段,将每组试验在不同阶段的样本均方差值绘制成统计直方图,如图3所示。
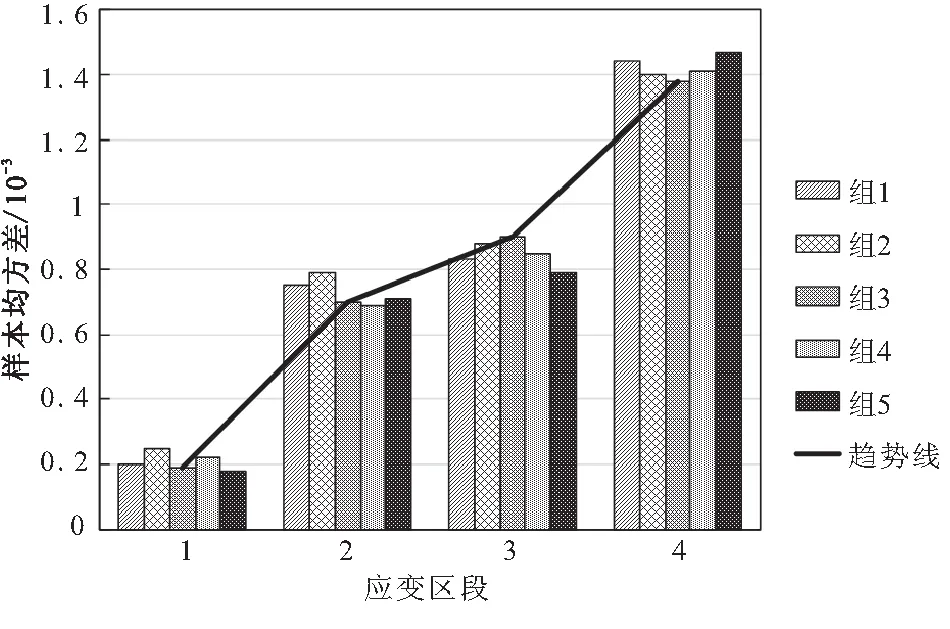
图3 泊松比散布统计直方图
图3表明,各组试件在相同应变条件下的泊松比散布差别较小,散布随应变的增大显著增加。因此,认为泊松比散布变化的主要原因是由于应变的增大,导致了力学性能的不确定,这一点从单因素方差分析表中随机偏差平方和SSE远小于应变偏差平方和SSε同样能够得出。由图中趋势线可得泊松比散布趋势变化较大,材料处于“线弹性区”(1区)时,如图2所示,应力应变呈线性关系,此时结构内部基本无损伤[11],泊松比散布处于较低水平,力学性能未出现明显的不确定性。材料处于“脱湿发生区”(2区)时,结构内部开始出现脱湿点,且随着应变的增大,脱湿损伤加剧[11],该阶段泊松比的散布迅速增大,主要是由于脱湿点的位置和各点损伤程度的不确定性分布,导致了力学性能的不确定。材料处于“应力平台区”(3区)时,脱湿损伤继续发生,颗粒/基体界面开始出现脱粘[11]。因此,该阶段泊松比散布仍处于较高水平,且比上一阶段有所增大。材料处于“趋于断裂区”(4区)时,粘合剂基体结构开始破坏,且很短时间内会出现宏观断裂[11],此阶段的泊松比散布大幅度增加,同时也表明材料趋近于失效时,力学性能将很难预测。
综合以上分析,力学性能参数测量结果的散布来源于力学性能的真实散布和测量过程带来的散布,而真实散布又包括确定变量(温度、加载时间、应变等)引起的散布和试件本身的性能差异,且测量过程和试件本身性能的波动是随机因素。方差分析将散布的总差异分解为变量引起的差异和单纯由随机因素引起的差异之和,变量引起的差异表明,固体推进剂力学性能的不确定程度不是固定的,而是随着某些确定变量发生变化的,在进行结构完整性评估时,应充分考虑力学性能散布及散布的变化范围;随机因素带来的差异控制在较低水平时,不会影响散布大小的变化规律,可忽略不计。
推进剂的力学性能应避免落在结构破坏的危险区域。如果将不会引起结构破坏的最大散布称为许用散布,则许用散布应能保证在任意变量组合条件下,结构破坏均不会发生,且应考虑具有一定的安全系数。药柱在生产、运输、贮存和使用过程中,应避免引入可能造成散布增大的因素,生产配方和工艺的改进应考虑确定变量对力学性能不确定度的影响规律,使任意因素组合条件下的散布均能完全控制在安全范围以内,即小于许用散布。
4 结论
(1)松弛模量的散布与温度和载荷作用时间具有明显的相关性。松弛模量散布随加载时间的增加逐渐降低;温度对散布的影响更加显著,随着温度的降低,松弛模量散布明显变大。
(2)泊松比的散布在不同的应变阶段差异较大。应变增大导致的结构损伤的不确定性是泊松比散布的主要来源;随着应变的增大,结构损伤加剧,泊松比散布显著增加。
(3)推进剂在趋于玻璃化转变和结构失效时,由于内部结构变化的不确定性,力学性能很难预测。
[1] 张海联,周建平.固体推进剂药柱松弛模量随机粘弹性有限元分析[J].推进技术,2001,22(4):332-336.
[2] 覃光明,卜昭献,张晓宏.固体推进剂装药设计[M].北京: 国防工业出版社,2013.
[3] 蒙上阳,唐国金,雷勇军.材料性能对固体发动机结构完整性的影响[J].国防科技大学学报,2002,24(5):10-15.
[4] 张海联,周建平.固体推进剂药柱泊松比随机粘弹性有限元分析[J].推进技术,2001,22(3):245-249.
[5] 王君祺,职世君,张建伟.非均布瞬态内压作用下固体推进剂药柱泊松比随机结构分析[J].固体火箭技术,2012,35(6):747-750.
[6] 刘冬青,孙冰,张建伟.固体推进剂药柱不确定结构分析及方法比较[J].航空动力学报,2013,28(2):466-472.
[7] 施陈波,汤海滨,张莘艾,等.mN级推力架静态特性及推力测量不确定度分析[J].固体火箭技术,2011,34(3):398-402.
[8] 胡松启,刘凯,王鹏飞,等.定容燃烧器法热损失率不确定度分析[J].含能材料,2013,21(1):97-102.
[9] Lal A,Raghunandan B N.Uncertainty analysis of propellant gauging system for spacecraft[J].Journal of Spacecraft and Rockets,2005,42(5).
[10] Evans J A.Monte carlo assessment of solid propellant burning rate measurement[D].Ann Arbor:The University of Alabama in Huntsville,2013.
[11] 常武军,鞠玉涛,王蓬勃.HTPB推进剂脱湿与力学性能的相关性研究[J].兵工学报,2012,33(3):261-266.
(编辑:刘红利)
Study on correlation between dispersion of mechanical property and certain variables of HTPB propellant
ZHANG Xiao,ZHENG Jian,PENG Wei,GU Zhi-xu
(Ordnance Engineering College,Shijiazhuang 050003,China)
The mechanical property of composite solid propellant disperses within a certain range even in the same condition.The correlation between the dispersion of relaxation modulus and Poisson's ratio and certain variables was studied by analysis of variance experiments.Variance analysis models of dispersion were established.The change rules of dispersion were analyzed and the reasons were discussed. The results show that temperature and loading time have significant impacts on relaxation modulus' dispersion,and the dispersion of Poisson's ratio at different stages has a very significant diversity.Uncertainty of structural damage is the major cause of the increase of Poisson's ratio's dispersion.The glass transition and structural failure can lead to great dispersion of mechanical property.
HTPB propellant;analysis of variance;dispersion of mechanical property;structural damage;relaxation modulus;Poisson's ratio
2014-05-09;
2014-08-21。
张晓(1990—),男,硕士,研究方向为固体推进剂力学性能。E-mail:erebuss@outlook.com
V512
A
1006-2793(2015)0378-05
10.7673/j.issn.1006-2793.2015.03.015

