论模糊综合评价法对公司内部控制的评价

奚瑞红

（黑龙江省教育学院，哈尔滨 150080）

一、公司内部控制综合评价方法

目前，国内外常用的内部控制评价方法主要有模糊评价法、专家评价法、层次分析法和其他数学方法[1]。本文将分析各种评价方法的优缺点及其适用范围，选择合适的方法进行内部控制综合评价研究。

1.专家评价法

专家评价法主要依据是专家的主观判断，通常用分数或是指数作为进行评价的标准，从而对评价的对象进行综合评价。这种评价方法比较简单，主要用于科研生产力的评价、大学研究成果的评价以及对公司经济效益的评价等。专家评价法的主要缺点是其主观性太强，只适用于比较简单的内部控制系统的评价和对比，对于比较复杂的评价对象则需要采用其他方法进行相应的评价。

2.层次分析法

美国运筹学家Saaty于20世纪70年代中期提出了层次分析法（the analytic hierarchy process AHP），它是系统工程中对于非定量的事件进行定量分析的一种方法[2]。AHP法一出现便很快得到了深入研究和广泛应用，在学术界引起了很大的反响。AHP法的核心思想是通过两两之间进行比较，构造出判断矩阵；也有学者先后提出了特征向量法、最小二乘法、几何最小二乘法、对数最小二乘法和最小偏差法[3]。AHP法自身也有一些缺点，比如，判断矩阵由专家给出，其一致性和专家评价法一样会受到主观因素和知识结构的影响。综合评价模型采用线性加权和式，有一定独立性的限制，不可以盲目应用。

3.数据包络分析法

美国Chames和Coope等人在1978年首次提出了数据包络分析法（data envelopment analysis，DEA），用于评价公司多输入和多输出的部门的相对有效性[4]。DEA模型C2R在1978年首次问世后，迅速引起了关注。在Chames和Cooper等人提出C2GS2模型后，魏权龄等人又提出了C2W模型，C2WH模型和C2WY模型。同时，在魏权龄《评价相对有效性的DEA方法》一书中，系统地阐述了DEA方法的理论依据及其应用。DEA方法通过对输入和输出的信息进行综合分析后，得到每个方案反映综合效率的数据指标[5]。

4.模糊综合评价法

模糊综合评价法由美国加州福尼亚大学的Randolph教授创立，用来定量描述边界模糊以及性状模糊的事物。其基本思想是，先对单个因素逐一进行评价，随后对所有的因素一起进行综合模糊评价，以防止遗漏任何信息，同时避免了确定性评价对客观真实的影响[6]。模糊数学侧重于解决多目标综合评价问题，针对定性信息较多的问题。模糊综合评价（Fuzzy Comprehensive Assessment）是模糊评价法中的重要方法之一，通过构建目标集合评定集进一步确定隶属度向量；接着，通过模糊映射得到多目标综合评价的结果[7]。FCA法能够较好地解决综合评价问题中的模糊性，适用于评价因素和结构层次较多的情况，在很多领域有着广泛的应用。

5.其他评价方法

（1）经济分析法。经济分析法主要有费用-效益分析法、给定综合指标公式或模型方法等。主要适用于新产品开发、经济效益和科技研究成果的评价、投资项目评价和区域经济发展不平衡程度等问题。优点主要是方便不同对象之间的比较，缺点是其模型很难建立。

（2）多目标决策法。多目标决策法主要分为分层序列法、重排次序法、对话法和直接求所有非劣解法等。随着计算机的广泛应用、知识工程、决策支持系统等的研发，多目标决策法的理论和方法的研究也不断深入，加快了管理决策科学化的进程。多目标决策法已经广泛的应用于社会、经济和工程等相关领域，且较为严密。

二、公司内部控制模糊综合评价模型

目前，国内外常用的评价方法主要有专家评价法、层次分析法、数据包络分析法和模糊评价法。每一种评价方法都各有其优缺点，上文已经进行了具体的分析。模糊综合评价法能够较好地分析综合评价中的模糊性问题，适用于评价结构层次和评价因素较多的情况。因此，本文着重用模糊综合评价方法对公司内部控制评价问题进行相关研究。

1.模糊综合评价法的基本思路

近年来，国内外对模糊综合评价项目的研究成果很多，但是，当模型中因素较多、权重难以确定时，需要对模型进行改进，成为多级模糊综合评价模型。通过建立公司内部控制因素集，对内部控制点进行权重的分配并给予评价，最后利用模糊矩阵对公司内部控制进行综合评价，并得到评价的结果。

影响公司内部控制效果的因素有很多，各个因素之间还有层次之分，此时采用多级综合评判法具有有效性。

该多级综合评判模型是由（F，P，V）3个集合构成的，其中，F代表被评价对象的因素集合，也就是被评价对象的各种特性：

P为评价集，也就是针对被评价对象给出的评价等级：

V是单因素评价矩阵。单因素评价矩阵是由评价集中每个因素评价隶属度的值组成的。对于因素集中每个因素判断后，就可以得到评价矩阵V：

式中：E、N分别为统计时间段(以班为例)的地音能量和频次值；Ei、Ni分别为最近i个班次能量、频次的平均指标值。

式中vij——表示因素fi和评价pj具有关系V的程度，且满足：

由于因素集F对评价结果的影响情况有所不同，需要给予每个因素不同的权重，从而得到各个指标的权重模糊集合W：

式中wi——表示第i个因素fi所对应的权重值，同时规定：

综合评价按照权重将单因素评价综合起来，用Z表示综合评价集，定义Z为：

式中：

利用上述方法进行评价时，如果评价因素较多，可以将各个因素按照平行、因果关系等划分成若干个子集合，对各个子集合分别进行一级综合评价，将得到的评价结果组合成单因素评价矩阵，并给予权重；接着进行矩阵的运算，从而得到二级综合评价的结果。在综合评价中，可以根据评价的不同情况，进行多次循环，以达到多级综合评价的目的，并得到相应的结果。

2.模糊综合评价模型的应用步骤

根据上述模糊综合评价法的基本思路，本文构建的BH公司内部控制模糊综合评价体系的具体步骤如下。

（1）确定指标体系。首先确定因素集为 F=（F1，F2，…，FN）；评语集为 P=（p1，p2，…，pm）。

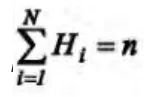
（2）确定单因素评判矩阵。判断所确定的因素集F中的每个因素对于评语集P中的评语的隶属度的大小，称为单因素评价。对因素集F中的每个因素都给予了判断，即可得到评价矩阵V，见式3。vij表示因素fi和评价pj具有关系V的程度，且满足式4所示条件。

（3）综合评判。首先需要进行初等评判，即对因素集中每个Fi=（Fi1，Fi2，…，Fihi）的hi个因素针对初始模型进行综合评判。假设因素Fi的重要程度模糊子集为，Fi中的hi个因素总评价矩阵为Vi，于是可以得到：

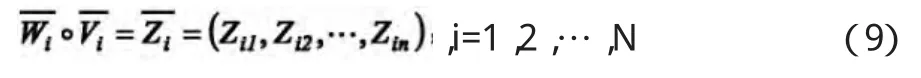
接着，进行二级评判。设反应 F=（F1，F2，…，FN）中因素重要程度的子集为，并且满足=（W1，W2，…，WN）；对因素集F来说，总的评价矩阵为：

（4）确立指标权重。在进行评价模型构建之前，需要将上述各个评价指标按照标度含义表将其相对重要程度予以列示，得到的便是各个评价指标的相对权重，如表1所示。

表1 指标标度含义

①一级评价指标权重的计算。通过调查问卷的方式获取各项参数在评价过程中所占的权重。由Frobinius定理可知，当Z为正矩阵时，其最大特征值所对应的特证向量是正的。因此为了保证权重为正，需要求解矩阵Z的最大特征值和其所对应的特征向量，并进行标准化处理。

应用AHP乘法进行求解，将判断矩阵的所有元素按照行相乘，即：

各行得到的乘积Ki分别开n次方，可以得到Mi'，即：

②指标评价特征的权重计算。本文根据公司内部控制评价体系的设置，结合评价指标所具有的影响性特征，在采用调查问卷方式的基础上将内部控制评价指标的特征总结为有效性、完整性、规范性和经济性四类，形成评价因素重要程度的子集。指标评价特征权重的计算过程和一级评价指标权重的计算过程相同。

（5）公司内部控制效果评价。在构建的指标体系和其随对应的权重进行了二级综合评价后，再对内部控制实施效果的四个特征进行综合性评价，得到内部控制整体评价的结果，如式12。

式中，Z为各个因素随对应的评价集，V为内部控制评价效果的评价集。

如果在综合评价过程中，每个子因素又包括了较多的因素，那么可以将子因素在进行划分，形成三级或是更高级的模型，从而实现多级综合评价。

[1]顾基发.评价方法综述.科学决策与系统工程[M].北京：中国科学技术出版社，1999：22-26.

[2]Saaty TL.Modeling Unstructured Decision Problems：the Theory of Analytical Hierarchies[J].Math and Modeling，1997，（1）：59-77.

[3]Chu A T，et al.AComparison of Two Methodsfor Determing the Weights of Belonging to Fuzzy Sets[J].Journal of Optimization Theory and Applications，1999，（27）：531-538.

[4]Chames A，Coope W.Measuringthe Efficiencyof Decision Making Units[J].European Journalof Operations Research，1978，（2）：429-444.

[5]魏权龄.评价相对有效性的DEA方法[M].北京：中国人民大学出版社，1988.

[6]Randolph P.Auditor Reputation and the Pricing of Initial Public Offerings[J].The Accountion Review，1989，13（1）：27-31.

[7]武小悦，李国雄.一种Fuzzy综合评价[J].系统工程与电子技术，1995，（4）：21-25.

[8]Dela Hostria.Interoperability of Standards to Support Application Integration[J].In Enterprise Inter-and-Intra Organisational Integration，2003，（2）：283-294.