粘弹性自由层阻尼薄板减振有限元研究

孙世威

摘要：本基于有限元的模态应变能法研究了粘弹性自由层阻尼薄板，建立粘弹性自由层阻尼薄板的有限元模型，进而求出其固有频率及损耗因子。然后使用工程经验公式对粘弹性自由层阻尼结构进行计算，计算其损耗因子，与有限元法进行对比，将有限元解与经验解进行对比。通过与工程经验解之间的对比给出了有限元法在分析类似问题上的有效性分析。

关键词：粘弹性；Ansys；模态应变能；损耗因子

中图分类号：TB535+.1 文献标识码：A 文章编号：1672-3791（2015）08（c）-0000-00

Finite Element Research on Damping of Viscoelastic Free Layer Damping Sheet

SUN Shi-wei1

（1. Hangzhou State Power Machinery Research & Design Institute， Hangzhou310000，China）

Abstract：Based on modal strain energy method， the paper discusses viscoelastic free layer damping sheet， establishesthe finite element model of it and obtains the natural frequencies and loss factor. Then the paper calculates the loss factor of viscoelastic free layer damping structure with engineering empirical formula， and compares the result with that obtained by finite element method. By comparing the two results， it indicates that the finite element method is effective in analyzing this kind of problems.

Key words：viscoelastic， Ansys， modal strain energy， loss factor

粘弹性阻尼材料具有高阻尼的特点，且能在较宽的频带内起到抑制振动和噪声的作用，因此广泛用于现代航空、航天、航海、交通运输、大型机械等领域，其形式主要是粘弹性阻尼复合结构。这种结构主要有两种传统的形式：自由阻尼层结构和约束阻尼层结构。约束阻尼层结构产生的减振降噪效果相对于自由阻尼层结构更好，因此这方面的研究也较多点。但自由阻尼层结构结构简单，适用范围广，工艺简单，因此工程上应用较广泛。

在国外，阻尼材料减振的理论研究始于上世纪五十年代，并于六、七十年代开始应用于航天结构。DIT.R.A 和MEAD.D.J给出了约束阻尼梁的振动方程。在此基础上，D.K.Rao分析了不同边界条件下约束阻尼梁的频率和损耗因子。

目前，国外对于约束层梁、板已经进行了大量的研究，早在60年代左右，Kerwin E M、Mead D J、Rao D K等人就已经对CLD 梁、板进行了研究[1-4]，随后不同的研究理论相继提出来进一步解决CLD 梁、板问题[5-6]。Vawani J、He s等人提出了CLD 梁的固有频率和损耗因子的计算方法[7-8]。

国内，阻尼减振技术也被广泛应用于汽车、航空航天等领域。钱振东推导了约束阻尼层板的运动方程和边界条件，分析了简支矩形板的固有振动。李恩奇等人采用复常量和复变量模型求出了固有频率和结构的损耗因子。

本论文以一端固定薄板为对象开展自由层阻尼振动抑制研究，建立板状自由层阻尼系统动力学模型，分析自由层阻尼板的动特性，研究板自由层阻尼减振机理、优化设计理论与方法以及工程应用规范。

同时由于对工程经验解和数值解的对比研究比较少，因此本文利用模态应变能法从数值和经验两方面研究一端固定的板的固有频率以及损耗因子。

1，粘弹性阻尼结构减振机理

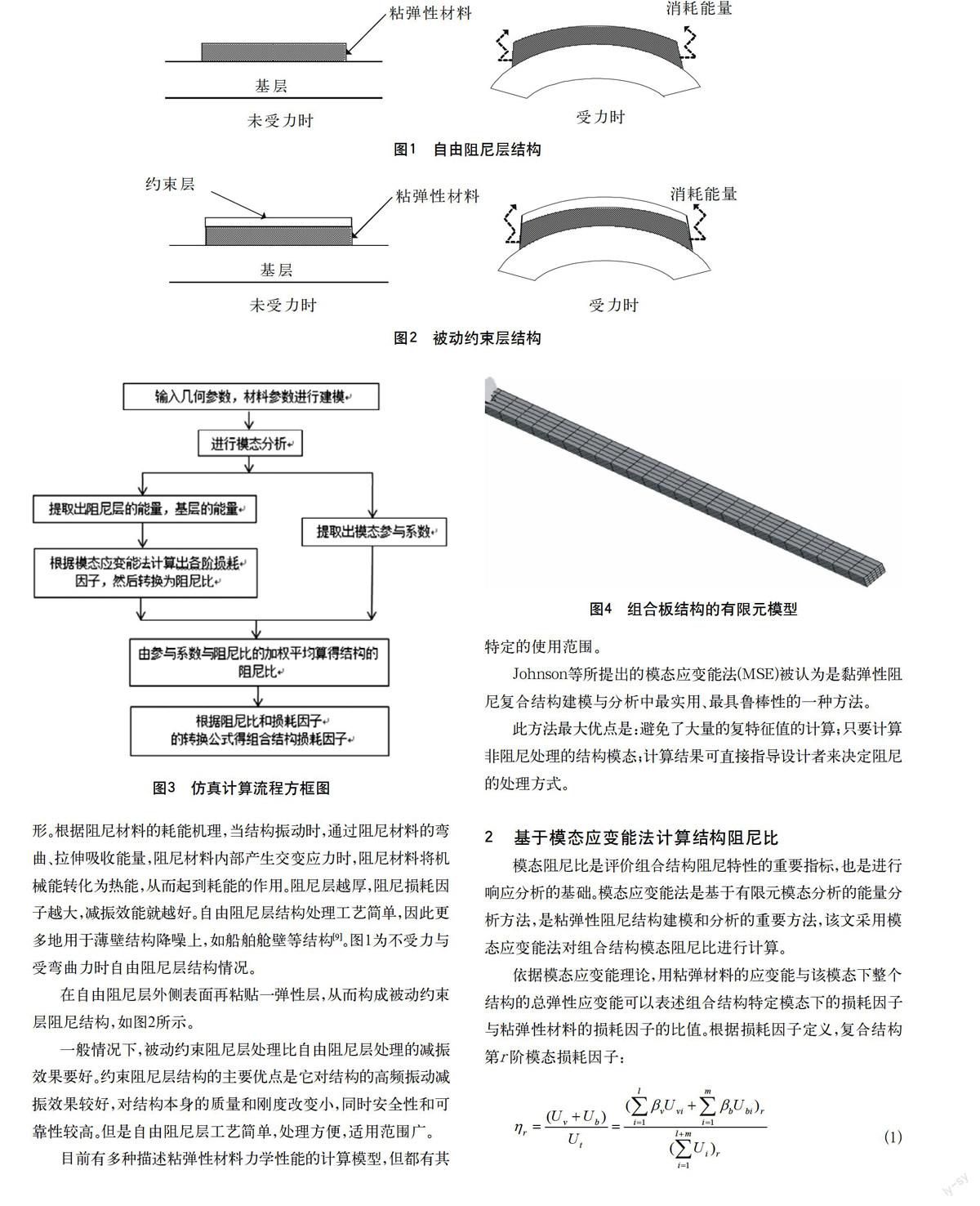
粘弹性阻尼材料的耗能机理主要是阻尼材料的剪切变形。自由阻尼层结构将一层阻尼材料粘贴于基层表面上，当基层产生弯曲振动时，阻尼层随基层一起振动，在阻尼层内部产生拉-压变形。根据阻尼材料的耗能机理，当结构振动时，通过阻尼材料的弯曲、拉伸吸收能量，阻尼材料内部产生交变应力时，阻尼材料将机械能转化为热能，从而起到耗能的作用。阻尼层越厚，阻尼损耗因子越大，减振效能就越好。自由阻尼层结构处理工艺简单，因此更多地用于薄壁结构降噪上，如船舶舱壁等结构[9]。图1为不受力与受弯曲力时自由阻尼层结构情况。

图1 自由阻尼层结构

在自由阻尼层外侧表面再粘贴一弹性层，从而构成被动约束层阻尼结构，如图2所示。

图2 被动约束层结构

一般情况下，被动约束阻尼层处理比自由阻尼层处理的减振效果要好。约束阻尼层结构的主要优点是它对结构的高频振动减振效果较好，对结构本身的质量和刚度改变小，同时安全性和可靠性较高。但是自由阻尼层工艺简单，处理方便，适用范围广。

目前有多种描述粘弹性材料力学性能的计算模型，但都有其特定的使用范围。

Johnson等所提出的模态应变能法（MSE）被认为是黏弹性阻尼复合结构建模与分析中最实用、最具鲁棒性的一种方法。

此方法最大优点是：避免了大量的复特征值的计算；只要计算非阻尼处理的结构模态；计算结果可直接指导设计者来决定阻尼的处理方式。

2，基于模态应变能法计算结构阻尼比

模态阻尼比是评价组合结构阻尼特性的重要指标，也是进行响应分析的基础。模态应变能法是基于有限元模态分析的能量分析方法，是粘弹性阻尼结构建模和分析的重要方法，本文采用模态应变能法对组合结构模态阻尼比进行计算。

依据模态应变能理论，用粘弹材料的应变能与该模态下整个结构的总弹性应变能可以表述组合结构特定模态下的损耗因子与粘弹性材料的损耗因子的比值。根据损耗因子定义，复合结构第 阶模态损耗因子：

其中， 是粘弹性材料的损耗应变能， 为光梁的损耗应变能，由于光梁的损耗因子较小，所以实际计算中，该项忽略不计， 为组合结构的总应变能。

分别为粘弹性材料和光梁的材料损耗因子， 代表两者各自的单元个数， 、 分别为粘弹性材料和光梁的单元应变能。

利用粘弹性组合结构的等效粘性阻尼比 和模态损耗因子 的关系：

得到结构的第 阶模态阻尼比 的表达式：

3，ANSYS仿真模型验证与讨论

本文中一端固支板的几何尺寸为205mm×10mm×4mm。其中基层和阻尼层厚度（H2，H1）均为2mm。选用solid186单元。基层和阻尼层所采用的材料如表1：

计算流程如下方框图所示：

为了模拟基层和阻尼层的黏合，用glue命令将上下两层实体的接触面黏合或划分网格后用merge命令来实现黏合效果。

在ansys中选择模态分析，使用lanczos法提取前六阶模态，同时用mXPAND， 6，，，YES 对前六阶进行扩展，最后求解。

仿真求解结束后，在后处理阶段可根据损耗因子的公式（1）编写后处理命令，使用如下命令：

etable，energy1，sene，elastic

ssum

*get，energy1，ssum，，item，energy1

求出各阶模态的损耗因子，然后根据阻尼比和损耗因子的公式（2），求出各阶模态阻尼比。

（4）

算出自由层阻尼结构一端固支薄板的损耗因子为0.0062，文献值[11]为0.0060763。考虑到软件版本和使用单元的不同，2.03%的误差是可以接受的。

自由层阻尼结构一端固支的薄板损耗因子和结构参数的经验公式[12-13]为：

ηs=ηeh（3+6h +4h2）/[1+eh（5+6h +4h2）] （5）

式中h =H2/H1，是阻尼层厚度H2与基本层厚度H1之比； e=E2/E1，是阻尼层杨氏模量E2与基本层杨氏模量E1之比；η为阻尼层材料的损耗因子；ηs为粘弹性自由层阻尼组合板结构的损耗因子。

将基层和阻尼层材料属性值代入：

ηs=0.5*0.96e-3*1（3+6*1 +4*12）/[1+0.96e-3*1（5+6*1+4*12）]=6.1514e-3

由于本文仿真时只提取了前6阶结果，因此结果与理论值有误差。提取尽可能多的阶数可以减小误差，阶数的提取多少可根据个人所需来设定。本文中的计算结果与文献中的结果十分吻合，证明了此方法的有效性。ANSYS模拟结果和经验公式的一致说明了建模的正确性，以及模态应变能法是可以用于对粘弹性阻尼组合结构进行分析的。

4，结论

本文依据阻尼材料减振的原理，在ANSYS软件中对粘弹性自由层阻尼的减振过程进行了仿真，用模拟得到的损耗因子与经验公式得出的结果相比两者基本吻合，验证了建模的正确性，同时说明了ANSYS中模态应变能法对于粘弹性阻尼材料的适用性。该方法操作简单， ，与理论方法相比较过程简单，思路清晰，与实验验证相比较，节省了人力，财力。

参考文献：

[1]. Kerwin E M. Damping of flexural waves by aconstrained viscoelastic layer [J]. Acoust. Soc. Am. 1959.

[2]. Mead D J ，Markus S. The forced vibration of athree-layer damped sandwich bam with arbitraryboundary conditions [J]. Sound Vibr. 1969.

[3]. Rao D K. Vibration of short sandwich beams [J]. SoundVibr. 1977.

[4]. Mead D J. Flexural vibration of damped sandwichbeams [J]. Sound Vibr. 1982.

[5]. Miles N N，Reinhall P G. An analytical model forthe vibration of laminated beams including the effects ofboth shear and thickness deformation in the adhesivelayer ASME[ J].Vibr. Acoust. 1986 ，108：56–64.

[6]. Frostig Y， Baruch M. Free vibrations of sandwichbeams with a transversely flexible core： a high orderapproach [J]. Sound Vibr. 1994，176：195–208.

[7]. Vaswani J， Asnani N T， Nakra B C. Vibration anddamping analysis of curved sandwich beams with aviscoelastic core. Composite Struct. 1988.

[8]. He S， Rao M D.Prediction of loss factors ofcurved sandwich beams [J]. Sound Vibr. 1992

[9]. 刘棣华. 粘弹阻尼减振降噪应用技术.北京： 宇航出版社， 1990：54-69.

[10]. 谭峰，粘弹性阻尼结构减振降噪分析及优化研究，上海交通大学，2010

[11]. 曹银萍，石秀华，邵鑫，自由阻尼悬臂梁减振理论及有限元研究，计算机仿真，2009，26（11）

[12]. 盛美萍，王敏庆，孙进才.噪声与振动控制技术基础[M].北京：科学出版社， 2001.

[13]. 戴德沛.阻尼减振降噪技术[M].西安：西安交通大学出版社， 1986.