超声波电动机P 与PI 型迭代学习转速控制

刘 玉，史敬灼，黄景涛，徐美玉，张聚伟，张 雷

(河南科技大学，洛阳471023)

0 引 言

超声波电动机特殊的运行机理，使其运行特性表现出明显的非线性及时变特征，不易得到理想的运动控制性能［1］。为克服超声波电动机自身的这些缺点，努力得到符合应用期望的控制性能和运行稳定性，其控制策略的研究逐渐趋于复杂化。许多复杂的控制器，如神经网络控制器、自适应控制器、模糊神经网络控制器等，先后被提出并用于超声波电动机。这些控制策略，算法复杂，不仅增加了系统复杂度，而且在线计算量大，其实现需要更高档的DSP 等芯片，从而增加了系统成本，不利于超声波电动机的大规模产业化应用。

我们当然希望控制策略越简单越好，但前提是电机系统控制性能满足工业应用要求。而之所以超声波电动机控制策略研究日渐复杂化，原因在于惯常使用的定常参数PID 等简单控制策略无法满足需要。于是，有必要探求其它的较为简单的控制形式和控制策略，并针对超声波电动机的特点进行合理改变、设计与整定，才有可能实现我们的期望。

Arimoto 等人在上世纪80 年代提出的迭代学习控制思想［2］，是一种通过模仿人类学习行为来获得学习能力的渐进控制过程［3］。该控制器在重复的运行过程中，基于经验知识学习来确定逐渐趋近期望控制过程的控制量最优变化轨迹，从而得到更好的控制性能［4］。迭代学习控制算法较为简单，不依赖于被控对象的精确模型，适用于超声波电动机这类具有高度非线性、模型难以准确确定且可重复运行的被控对象。

本文针对超声波电动机的时变非线性，分别设计了形式简单的P 型和PI 型迭代学习控制策略，对超声波电动机进行转速控制。实验表明，控制算法简单，易于实现，电机转速响应曲线表现出渐进的学习过程，控制效果较好。

1 迭代学习控制的基本算法

迭代学习控制策略针对具有可重复性的被控对象，利用先前的控制经验，根据该系统的输入变量和输出期望信号之间的相互关系，来在线寻求一个理想的输入变量变化过程，从而使被控对象达到控制要求并输出期望的输出信号。这里所谓的可重复性，有两层含义。一是系统的运动是重复的;对于电机转速控制来说，即指其转速给定信号是重复施加的，电机每次运行均具有相同的期望输出转速。二是在上述每一次的重复运行过程中，被控对象的向量函数及其相互之间的函数关系是不变的。

作为普通和精密运动控制执行部件的超声波电动机，经常工作于具有重复性的运动控制场合。据此，采用迭代学习控制方法，有可能通过相对简单的控制器形式、较小的在线计算量，利用电机运动的重复性，实现电机控制性能的渐进调整，并在有限次数的重复运动之后，达到较好的控制性能。这就为降低超声波电动机系统的控制复杂度提供了一种新的可能思路。

迭代学习控制的基本控制规律:

式中:t 为时间;uk+1(t)为系统第k +1 次重复运行过程中，在t 时刻的控制器输出控制量，本文取为超声波电动机的驱动频率值;uk(t)为系统第k 次运行过程中t 时刻的控制量;ek(t)为系统第k 次运行过程中t时刻的转速误差;Nref(t)为电机转速给定值;n(t)为电机的实际转速值;比例环节KP为学习增益。因学习律为比例环节，式(1)的控制规律又称为P 型迭代学习控制。

迭代学习控制的目的是在系统结构和参数都未知的前提下，经过多次重复运行，控制器的输出u(t)趋近于事先未知的ud(t)，从而使得电机转速n(t)趋近于期望的Nref(t)。当达到控制要求的精度之后，停止迭代学习并保存最近一次运行的控制器输入输出数据，就完成了迭代学习过程。

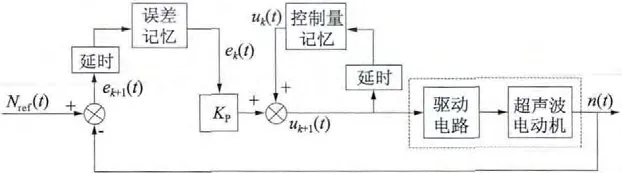
图1 超声波电动机迭代学习控制系统基本框图

图1 给出了超声波电动机迭代学习转速控制系统的基本结构框图。图中“控制量记忆”、“误差记忆”与“延时”环节用来存储以前运动过程中的控制量和误差，KP环节表示学习控制律。这些环节构成了迭代学习控制器，对应于式(1)。显然，采用不同的学习控制律，可以得到不同的学习过程和控制过程。系统中，控制器的输出为超声波电动机频率的给定值，通过驱动电路给出具有相应频率的驱动电压作用于超声波电动机。与电机同轴刚性连接的旋转编码器检测电机转速得到反馈信号，其与转速给定值之差作为控制器的输入，进而通过重复的迭代学习控制，得到更好的控制过程。

考察式(1)与图1，系统当前控制过程的控制量uk+1(t)是由前次的控制量uk(t)和误差ek(t)计算得到的，即控制量与当前的系统输出转速误差ek+1(t)无关。从这一点来看，图1 系统实质上是一个开环控制系统。如前述，迭代学习控制是针对具有可重复性的系统提出的，其可重复性包含被控对象及其系统的时不变性质。对于时不变系统，采用式(1)计算控制量，能够保持控制的有效性，因为在每一次重复的控制过程中，控制对象的特性始终保持不变，变化的只是随机的扰动信号。由于随机扰动的量值通常微小，采用式(1)有可能保证并加快系统学习过程的收敛。但是超声波电动机具有明显的时变特性，采用式(1)与图1 形式进行控制，不能保证系统控制过程的有效性。实验表明，在阶跃转速给定值情况下，会导致电机转速跟踪过程中的抖动和稳态的转速偏差。因而，本文将式(1)改为:

式中:ek+1(t)为系统第k+1 次运行过程t 时刻的转速误差。对应于式(3)的控制系统框图如图2 所示，控制形式进一步简化。

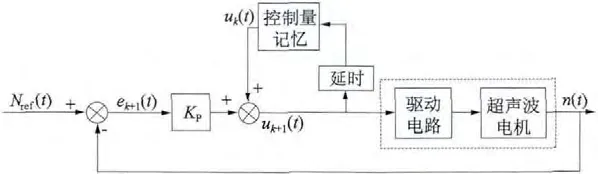
图2 超声波电动机改进迭代学习控制系统基本框图

式(3)控制量与当前转速误差相关。从单次控制过程来看，具有闭环控制的性质，为克服超声波电动机的时变特性提供了可能。从多次重复控制过程来看，每次的控制量都是在记忆前次控制量的基础上，根据时变对象当前的误差信息进行修正，同样具有迭代学习的特征，能够通过迭代使控制过程渐好。考察式(3)、图2 控制过程的在线计算量，与传统的固定参数PID 控制器相比，仅增加了控制量的一次存储与读取操作，计算量相当。

2 P 型迭代学习转速控制

2.1 学习增益KP 的确定

采用式(3)对超声波电动机进行转速控制，学习增益KP是唯一需要确定的控制参数。该值不仅与单次控制过程的动态性能相关，而且直接决定了迭代学习过程是否能够收敛。为得到学习过程的收敛条件，进而确定合适的KP值，首先取超声波电动机的模型为状态方程形式，并设为具有普遍意义的全局Lipschitz 连续动力系统状态方程［4］:

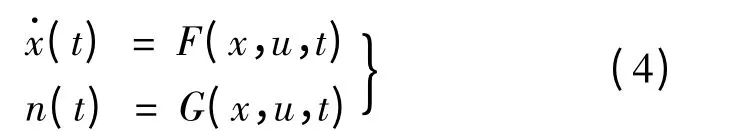
式中:x(t)为超声波电动机系统的状态变量。根据式(4)，可以推导出迭代学习的收敛条件［4］:

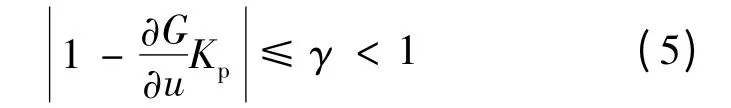
式中:γ 为小于1 的常数。限于篇幅，具体推导过程请参考文献［4］。式(5)给出了能够保证学习收敛的KP取值范围。

式(4)中，函数关系G 表征了超声波电动机转速n(t)与其控制量u(t)(本文为电机驱动频率)之间的函数关系。与之对应，式(5)中的偏导数代表了n(t)相对于u(t)的变化率。对于线性被控对象，这个偏导数通常为固定值。而对于超声波电动机这类非线性对象而言值随电机运行状态参数的不同而变化。

本文实验用电机为Shinsei USR60 型两相行波超声电机。文献［5］对该型电机做了详细测试，给出了电机转速与驱动频率之间的稳态关系曲线数据如图3 所示。据此，在实验电机运行频率范围内，可得到转速相对于驱动频率的变化率，即稳态的数值。显然，不同频率情况下，数值有差别。若采用工作频率范围内的最大值代入式(5)进行计算，得到的KP值能够保证在超声波电动机工作范围内的学习收敛性。由图3，经数据拟合计算得到的最大值为121.0 r/(min·kHz)。由式(5)收敛条件可得KP的取值范围为0 ＜KP＜0.017。仿真校核表明，这一取值范围可同时保证系统控制的稳定性。考虑实验程序中采用频率控制字来调节频率，考虑其数量变换关系，程序中KP的实际取值范围为0 ＜KP＜10.58。

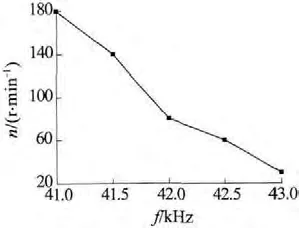
图3 转速和驱动频率关系(空载，实测)

2.2 实验分析

设定转速阶跃给定值为30 r/min，进行P 型迭代学习实验，希望得到超调为0 且响应速度较快的阶跃响应。实验用驱动电路为H 桥结构，采用相移PWM 控制方式。

迭代学习控制过程是通过记忆前次控制过程，逐步学习不断改进的过程。在这个过程中，首次控制过程因为没有前次记忆，无法进行学习，仅为其后控制过程提供第一次记忆作为学习基础。所以，可采用任意控制器进行首次控制。为便于说明学习效果，实验中采用KP=3.5、KI=2 的PI 控制器进行首次控制。该控制器可以保证超声波电动机系统的稳定运行，但控制效果不够理想，响应时间较长。首次运行过程中，记忆控制器输出的控制量。从第二次控制过程开始，采用改进的P 型迭代学习控制律式(3)作为控制器。

实验表明，学习增益KP在(0，10.58］范围内取不同值，学习过程都能够逐渐趋于收敛。KP值越大，学习收敛越快，转速阶跃响应的超调越大。例如取KP=3.5，连续进行9 次迭代学习控制的阶跃响应实验，得到9 次转速响应如图4 所示。

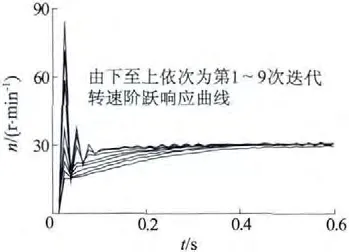
图4 转速阶跃响应曲线(KP =3.5)

图4 中，第8、9 次阶跃响应的超调明显增大。考虑到期望无超调，且学习导致的曲线其它部分变化已不明显，故而停止迭代学习。由图4 可以看出，随着迭代学习次数的增加，控制强度逐渐加强，阶跃响应上升时间逐渐减小，最终都会稳定在给定值，P型迭代学习策略是有效的。

图4 阶跃响应的一个突出问题是，随着迭代学习过程的持续进行，出现了明显的超调，这不是我们期望的。从现象上看，因为阶跃给定值在起始时刻跳变为非零的固定值(30 r/min)，而电机转速在起始时刻为0，于是得到较大的转速误差。考察式(1)或式(3)给出的控制策略，较大的起始转速误差必然导致起始控制量随着迭代的持续而快速增大，从而导致超调。

从原理上讲，迭代学习控制策略在本质上是一个在线的控制响应优化过程，P 型迭代学习采用了最简单的比例渐近优化策略。这一优化过程试图“渐近”的目标，是减小控制误差，即，使响应曲线不断趋近于给定值曲线。这也就是说，给定值曲线表达了我们的控制期望。实验中，给定值为固定值阶跃信号，如图5 中虚线所示。显然，考虑到包括超声波电动机在内的任何被控对象都会有惯性，转速响应曲线绝对不会和图5 虚线重合，于是P 型学习得到了转速数据点分布在图5 虚线上、下的响应曲线，即出现了超调。既然图5 虚线是不可能达到的，这样的曲线也就没有真实反映合理的控制期望，这是出现超调的重要原因之一。应该采用恰当的方式，表达合理的控制期望。据此，对转速阶跃给定值做柔化处理:

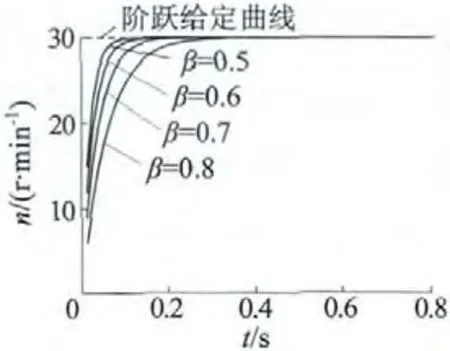
图5 柔滑的阶跃转速给定曲线

取KP=3.5、β=0.7，进行P 型迭代学习控制实验，连续9 次阶跃实验结果如图6 所示，控制性能指标变化如表1 所示，转速响应曲线逐渐趋于表征控制期望的柔化给定曲线，无超调。从表1 可以看出，从第六次实验开始，转速稳态波动误差增大。增加KP值进行实验。实验结果表明，KP值越大，迭代学习收敛速度越快，但稳态波动误差也增大。

表1 P 型迭代学习控制性能指标(KP =3.5，β=0.7)

上述P 型迭代学习控制实验中，电机能够无超调运行，通过迭代学习，电机控制性能逐渐趋好。控制参数取为KP=3.5，β =0.7 时，电机的转速控制性能较好，但转速响应曲线的上升时间还是比较长。当增加KP即增加控制强度之后，上升时间有所减小，但会导致较大的稳态波动误差。同时，迭代学习控制过程虽能够单调收敛，但趋近期望响应曲线时，收敛速度放慢，学习过程对控制性能的改进量变小。

考察控制策略式(3)，其中仅有一个控制参数KP，其值的确定需要同时兼顾动态、稳态控制性能及学习收敛性能。对简单的被控对象，也许可以设定一个KP值，使得这几种不同的性能要求得到较好的折衷。但对于复杂对象，例如超声波电动机，虽然能够通过记忆、学习，实现控制性能渐进，但显然无法兼顾上述几种性能要求。基于此，考虑在式(3)中增加误差的积分项，构成PI 型迭代学习控制，以期获得更好的控制性能。

3 PI 型迭代学习转速控制

3.1 PI 型迭代学习控制策略

在式(3)中增加误差的积分项，得PI 型迭代学习控制策略:

式中:KI为积分学习增益。增加转速误差的积分项，有可能在增大控制强度的同时抑制超调，减小稳态转速波动，使系统运行更加平稳。

3.2 实验分析

PI 型迭代学习控制的实验步骤与P 型迭代学习控制相同。选取不同的KP、KI、β 值进行阶跃响应实验，考察控制参数对控制和学习性能的影响。实验表明，选取KP=2、KI=6、β =0.8 时，性能相对较好，对应的阶跃响应迭代学习过程如图7 所示，控制性能指标如表2。由表2 中数据可以看出，学习过程的渐进性明显，稳态转速波动也相对较小。

表2 PI 型迭代学习控制性能指标(KP =2，KI =6，β=0.8)

4 结 语

本质上，迭代学习控制策略是一种算法相对简单的在线优化控制策略。为寻求适用于超声波电动机的简单控制策略，本文尝试将其用于超声波电动机转速控制，并根据超声波电动机的时变特点给出了改进的控制算法。实验表明，所设计的超声波电动机转速迭代学习控制器，能够实现在线的控制性能改进;适当表述的期望控制响应对控制性能及学习过程都有显著影响，需要根据控制性能要求确定;控制参数个数应适当，在考虑控制算法简单的同时，保证控制的有效性。

［1］ 史敬灼.超声波电机运动控制理论与技术［M］. 北京:科学出版社，2011:1 -19.

［2］ 方忠，韩正之，陈彭年. 迭代学习控制新进展［J］.控制理论与应用，2002，18(2):161 -166.

［3］ 于少娟，齐向东，吴聚华. 迭代学习控制理论及应用［M］. 北京:机械工业出版社，2005:6 -10，32 -103.

［4］ 许建新，侯忠生. 学习控制的现状与展望［J］. 自动化学报，2005，31(6):131 -143.

［5］ CHEN T C，YU C H，TSAI M C.A novel driver with adjustable frequency and phase for traveling -wave type ultrasonic motor［J］.Journal of the Chinese Institute of Engineers，2008，31(4):709 -713.