船用低压断路器短路保护动态特性仿真及其应用
黄 靖,沈 兵,杨 锋
(海军工程大学电气工程学院,湖北武汉430033)
0 引言
船舶电力系统为实现保护的选择性,一般基于电流原则和时间原则,依据短路电流估算结果和经验参数,对上下级断路器的动作电流和动作时间进行整定,未能考虑到断路器的短路保护动作特性,保护装置的保护选择性有待进一步的分析和校核。
通过断路器特性分析和计算,建立断路器仿真模型及船舶电力系统仿真模型,通过大量的仿真实验,可以全面分析上下级断路器在各种系统运行状态和故障状态下的保护选择性,并可根据仿真结果,优化断路器整定,提高其保护选择性,节省断路器试验所需的大量经费和时间。
围绕低压断路器的开断特性分析和断路器仿真建模,国内外学者开展了大量研究工作,建立了较为成熟的方法体系,其中最有代表性的是基于虚拟样机技术的低压断路器仿真建模方法[1-4]。但多数研究仅以单个断路器作为研究对象,对不同类型、容量的一组断路器在典型电力系统的典型故障状态下的保护动作特性和保护选择性尚未开展研究。
本文应用三维有限元软件Ansoft的瞬态求解器对某系列船用低压断路器的瞬动电磁脱扣器的静态电磁力矩特性进行计算,并结合脱扣器机械运动方程和Cassie开关电弧模型,基于电力系统仿真软件PSCAD/EMTDC建立断路器仿真模型,并通过实验和仿真对比分析,对断路器仿真模型参数进行修正。最后,基于PSCAD/EMTDC建立了典型船舶配电系统仿真模型,对配电系统断路器的保护选择性进行仿真分析。
1 电磁脱扣器静态电磁力矩分析
本文将某系列船用低压塑壳式断路器 (额定电流分别为200 A和400 A)及框架式自动空气断路器 (额定电流为1 000 A)作为研究对象。首先应用三维实体造型软件UG建立脱扣器三维模型。以额定电流为200 A的塑壳式断路器为例,其瞬动电磁脱扣器的三维模型如图1所示。该脱扣器电磁铁为拍合式,无铁心,衔铁和磁轭构成了主要磁通回路,载流导体形状不规则。

图1 200A塑壳式断路器内脱扣器三维模型Fig.1 3-D model of trip in 200A molded case circuit breaker
将脱扣器三维模型导入有限元软件Ansoft,应用其有限元求解器,对断路器脱扣器电磁特性进行仿真。图2给出了在激励电流达到17.8 kA时的脱扣器衔铁及磁轭磁感应强度B矢量分布。

图2 电磁脱扣器衔铁及磁轭磁感应强度B矢量分布Fig.2 Distribution of magnetic induction density vector in armature and yoke of trip
脱扣器电磁特性与电流激励和衔铁与磁轭之间的工作气隙密切相关,因此需要确定电磁力矩关于电流激励i和工作气隙 (以衔铁和磁轭端面夹角θ来度量,如图3所示)的定量关系。
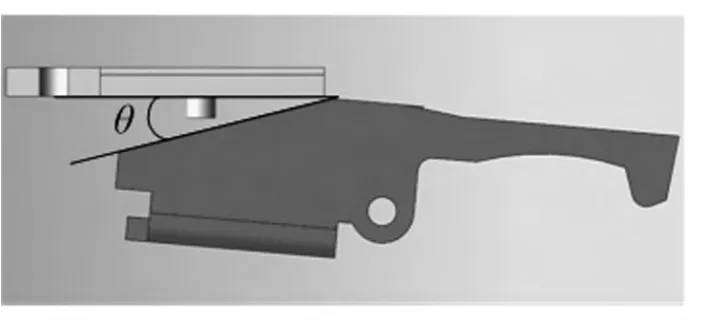
图3 衔铁与磁轭端面夹角θ示意图Fig.3 The angleθbetween armature and yoke
本文将载流导体电流i及夹角θ在其规定范围内分成几段,利用有限元软件Ansoft求出不同衔铁转角时各电流值所对应的电磁转矩,获得电磁转矩Te关于i和θ的二维数据表格及曲线,为断路器仿真模型的建立提供插值数据。
如图4给出了额定电流为200 A,400 A和1 000 A的断路器脱扣器衔铁电磁转矩T随i和θ变化的特性曲线。图中,由初始衔铁与磁轭夹角向夹角减少(即气隙减小)的方向转动的角度记为负,反之记为正。

图4 各断路器的脱扣器衔铁电磁转矩特性Fig.4 Electromagnetic torques on armatures of each circuit breakers with different current and the angleθ
2 断路器数学模型
2.1 脱扣器衔铁运动方程
该系列塑壳式和框架式断路器均采用了拍合式脱扣器,其衔铁的运动方程可表示如下[4]:
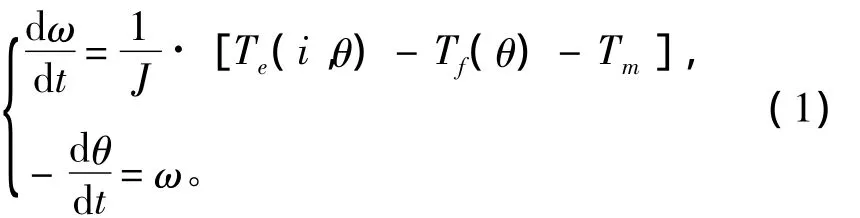
式中:θ为衔铁与磁轭端面夹角 (对于塑壳式断路器)或衔铁端面与水平方向夹角 (对于框架式断路器);ω为衔铁角速度;i为激励电流;Te为衔铁电磁力矩;Tf为弹簧反力矩;Tf包括反力弹簧反作用力矩和脱扣力矩两部分,后者为衔铁带动脱扣轴转动时受到的反作用力。Tm为摩擦力矩;J为衔铁转动惯量。脱扣力矩仅在衔铁带动脱扣轴转动的一定角度范围内起作用。
对于该系列塑壳式断路器,其反力矩由扭转弹簧提供,其反力矩Tf可按式(2)计算:

式中:θmax为衔铁与磁轭最大 (初始)夹角;θmin为衔铁与磁轭最小 (最终)夹角;θ1为脱扣力矩终止夹角;θ2为脱扣力矩起始夹角;θ0为反力弹簧初始扭转角度;M'为扭转弹簧刚度;Tr为平均脱扣力矩。
对于该系列框架式断路器,其反力矩由压缩弹簧提供,其反力矩Tf可按式(3)计算:

式中:θmax为衔铁与水平方向最大 (初始)夹角;θmin为衔铁与水平方向最小 (最终)夹角;θ1为脱扣力矩终止夹角;θ2为脱扣力矩起始夹角;d为压缩弹簧初始压缩长度;l衔铁轴心到反力弹簧作用点直线距离;P'为压缩弹簧刚度;Tr为平均脱扣力矩。
衔铁转动过程中的摩擦力矩相对于电磁力矩和反作用力矩来说很小,在计算中忽略不计。电磁脱扣器机械运动特性参数如表1所示。
2.2 断路器电弧模型
断路器分断时电弧生成和熄灭的过程是涉及机械运动、热、气和电磁等物理量的综合过程,情况复杂。黑盒电弧模型遵循能量的一般规律,将触头机械运动及电弧内部各种物理场的变化过程,用电弧电压随电弧位移或时间的宏观变化规律描述。经典的黑盒电弧模型有 Mayr模型[5]、Cassie 模型[6]等。其中Cassie电弧模型是影响和应用较为广泛一种黑盒模型。

表1 脱扣器机械运动特性参数Tab.1 Mechanical movement parameters of trips
Cassie电弧模型可表示为:

式中:g为电弧电导;u为电弧电压;Uc为电弧电压梯度,它是电弧瞬态恢复电压 (TRV)表示方法中的参考电压,取为TRV的峰值,在静态时是常数,与电流值无关;τc为Cassie电弧模型定义的时间常数。
黑盒电弧模型能够较为准确地描述电弧宏观电导变化规律,符合断路器模型的设计需求,且便于实现电路及系统仿真。本文采用Cassie电弧模型用于表述断路器开断电弧过程。
3 断路器仿真模型及其实验校验
3.1 断路器仿真模型设计
本文在断路器数学模型的基础上,基于电气系统专业仿真软件PSCAD/EMTDC建立了断路器仿真模型。以200 A塑壳式断路器为例说明单相瞬动脱扣器仿真模型,如图5所示。
塑壳式断路器瞬时保护动作环节按照塑壳断路器衔铁运动方程设计。其中的自定义模块“Te_200A”提供衔铁电磁力矩数据。该模块存储了电磁转矩Te关于电流i和衔铁与磁轭夹角θ的二维数据表格。在动态仿真过程中,模块“Te_200A”读取当前系统短路电流瞬时值i和夹角变量θ的大小,运用式(5)所示的二元三点插值公式[4]对二维数据表格进行插值计算,以获得当前状态下的电磁转矩Te。

图5 200A塑壳式断路器的电磁脱扣器仿真模型Fig.5 Simulation model of trip in 200A circuit breaker

式中:θ为衔铁与磁轭夹角的一维数据矩阵;I为激励电流的一维数据矩阵;Te为电磁转矩的二维数据矩阵。
弹簧反力由当前夹角θ决定,一旦电磁力矩大于弹簧反力,则通过2个积分环节 (分别得到衔铁角加速度和角速度)可算出θ随时间t的变化量及当前量。当θ1≤θ≤θ2时,衔铁还要附加平均脱扣反力矩;当θ<θ1时,可认为已满足脱扣条件,则输出跳闸信号。各相脱扣器仿真模型分别计算各自衔铁夹角θ,任意一相脱扣器衔铁夹角θ满足脱扣条件,则认为脱扣器脱扣。
脱扣时刻到动、静触头开始斥开时刻之间的操作机构解锁动作时间,文献[3-4]均提到其相对于脱扣器动作时间较短。另一方面,操作机构设定相对固定,一般不随断路器额定电流的变化进行调整,动作时间随短路电流大小的变化较小,其对断路器分断的宏观特性影响较小。在仿真模型中通过设置延时环节,并采用经验参数进行模拟。断路器电弧仿真模型如图6所示。

图6 电弧仿真模型Fig.6 Simulation model of arc model
电弧模型等效于一个串联于电路中阻值可控的可变电阻,用以模拟开关电弧等效电阻值。自定义计算模块(Cassie_Arc_Model)接收到脱扣器跳闸信号后,基于隐式梯形法[7]对Cassie电弧方程进行差分求解并输出电弧等效电阻的阻值以作用于系统电路。对式(4)按隐式梯形法求得差分方程:

式中:Δt为仿真计算步长。因u(t+Δt)无法获取,需通过预测代替:
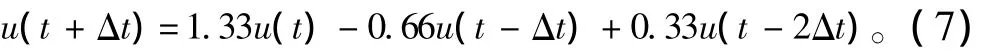
基于经验参数,并通过将实验数据与仿真数据比对校验,可得到电弧模型参数如表2所示。

表2 电弧模型参数Tab.2 The parameters of arc model
3.2 实验验证
为验证断路器仿真模型并校验参数,对该系列断路器进行短路分断实验。实验系统如图7所示。
实验电路通过可调电抗器控制短路电流,使短路电流有效值峰值达到预期短路值,然后接入断路器进行短路分断实验。通过电流互感器、多通道波形记录仪等记录试验数据。以200 A的塑壳式断路器为例,设定预期短路峰值电流为199 kA,塑壳式断路器瞬动脱扣电流的额定电流倍数(Ir3/Ie)整定为10倍。短路分断实验波形如图8所示。

图7 实验系统线路原理图Fig.7 Schematic circuit of experimental system

图8 200A塑壳式断路器短路分断实验电流波形图Fig.8 Short circuit breaking test of 200A circuit breaker

图9 200A塑壳式断路器短路分断仿真电流波形图Fig.9 Short circuit breaking simulation of 200A breaker
根据实验系统电路及参数,建立仿真系统。短路分断仿真结果如图9所示。
由图9可见,短路仿真波形与实验波形特征一致。由表3可看出,仿真值与实验值的相对误差不超过9%,验证了断路器仿真模型及参数的准确性,满足系统保护特性仿真的精度要求。

表3 仿真与实验结果Tab.3 Results of simulation and experiment
4 船用低压断路器保护选择性仿真分析
4.1 算例系统
将断路器仿真模型与发电机组、馈线和负载仿真模型相结合,可建立船舶配电系统仿真模型。算例系统如图10所示。图中G1为某型船用发电机组,额定功率为1 500 kW,额定电压为400 V,额定功率因数0.8,采用相复励励磁方式。线路参数如图10所示。DW1为额定电流1 000 A的框架式断路器,DZ1,DZ2分别为额定电流400 A和200 A的塑壳式断路器。DW1,DZ1,DZ2的瞬动脱扣电流的额定电流倍数(Ir3/Ie)均整定为10倍。设置故障点F1如图10所示,本文给出三相相间对称短路故障类型分析结果。

图10 算例系统仿真模型Fig.10 Simulation model of test system
4.2 短路仿真结果分析
故障点F1短路仿真结果如图11所示。
仿真结果表明:最大 (B相)短路电流峰值达到了12.10 kA,远大于塑壳式断路器DZ1和DZ2的瞬动整定值。短路故障发生后,DZ2和DZ1的B相脱扣器衔铁分别经过0.3 ms,0.8 ms开始转动,前者经1.9 ms即达到脱扣角度使断路器脱扣跳闸,短路电流开始分断,而后者经2.7 ms也达到脱扣角,此时B相电弧电流仍达到10.12 kA,此时衔铁所受电磁力矩仍远大于反作用力矩,DZ1随之脱扣跳闸。DZ1,DZ2均跳闸,DW1未跳闸,系统保护选择性失效,可见在船舶电力系统中,上下级线路短路电流水平相差不大,且上下级塑壳式断路器瞬动保护特性在大短路电流下十分接近,保护参数整定不合适时,将导致选择性保护失效。

图11 故障点F1仿真结果Fig.11 Simulation results of fault test F1
4.3 断路器整定参数的改进及仿真分析
为改善系统保护的选择性,在仿真系统中将DZ1,DZ2的瞬动电流倍数整定值(Ir3/Ie)修改为20倍和8倍。仿真得到F1点短路时DZ1的电磁转矩和反作用力矩,B相脱扣器衔铁与磁轭夹角波形如图12所示。
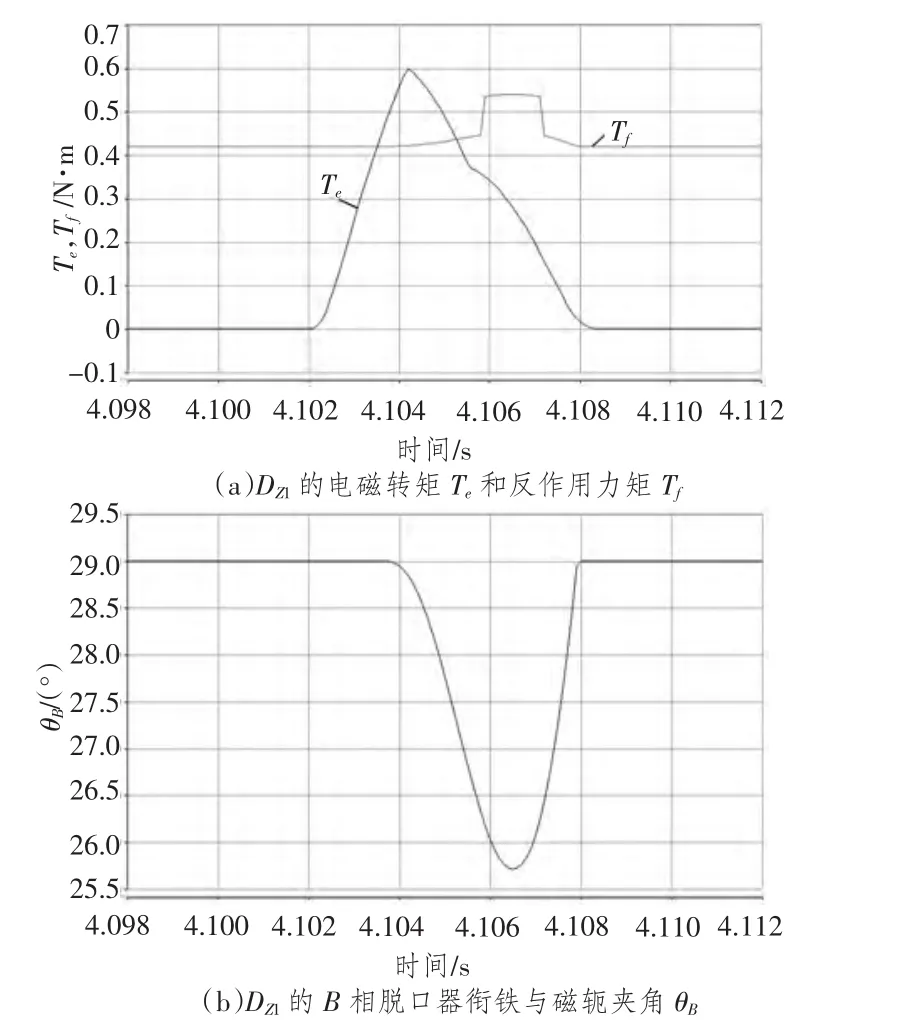
图12 整定参数调整后的仿真结果Fig.12 Simulation results with parameters adjustment
仿真结果表明:短路电流分断过程中,DZ1的B相脱扣器衔铁未达到脱扣角,DZ1和DW1均未断开,DZ2跳闸断开,达到了选择性保护的要求,从而仿真校验了DZ1,DZ2选择性保护整定的有效性,可作为实际系统中改善断路器保护整定的重要参考。
5 结语
1)应用ANSOFT分析了某系列船用低压断路器瞬动电磁脱扣器的电磁力矩特性,结合其机械运动方程及开关电弧模型,基于PSCAD/EMTDC建立了低压断路器仿真模型。验证实验表明,仿真与实验结果相对误差小于10%。
2)基于断路器仿真模型,建立了典型船舶电力系统仿真模型,并对算例配电网的典型短路故障进行了仿真分析。仿真结果表明,船舶电力系统保护选择性与系统参数、断路器保护动作特性及其整定参数密切相关。断路器参数整定不当时,存在保护选择性失效的风险。
3)本文设计的船用低压断路器仿真模型可用于船舶电力系统短路保护性能分析,对优化断路器结构设计和动作参数整定具有重要的参考价值。
[1] SHOKICHI T,YOSHIAKI T.Numerical analysis of electromagnetic forces in low voltage AC circuit breakers using 3-D finite element method taking into account eddy currents[J].IEEE Transactions on Magnetics,1998,34(5):2597-2600.
[2] 向洪岗,陈德桂,李兴文,等.应用有限元方法分析塑壳断路器磁脱扣器的动作特性[J].西安交通大学学报,2005,39(8):890 -894.
[3] 吴翊,胡正勇,黄蓉蓉,等.万能式断路器操作机构运动特性仿真分析[J].低压电器,2011(12):4-7.
[4] 陈德桂,李兴文.低压断路器的虚拟样机技术[M].北京:机械工业出版社,2009.
[5] VANDER S L,RUTGERS W R,KOREMAN C G A.A physical arc model for the simulation of current zero behavior of high voltage circuit breaker[J].IEEE Transactions on Power Delivery,1992,7(2):1016 -1022.
[6] MOKHTARI H,HEJRI M.A new three phase time-domain model for electric arc furnaces using MATLAB[J].IEEE Conference on Transmission and Distribution,2002:2078 -2084.
[7] DOMMEL H W.电力系统电磁暂态计算理论[M].李永庄,林集明,曾昭华,译.北京:水利电力出版社,1991:293-294.

