双轴向不同拉伸速率下丝素蛋白/聚己内酯复合纳米纤维膜的力学性能

王敏超，熊 杰，2

(1.浙江理工大学材料与纺织学院，浙江 杭州 310018;2.浙江理工大学先进纺织材料与制备技术教育部重点实验室，浙江 杭州 310018)

双轴向不同拉伸速率下丝素蛋白/聚己内酯复合纳米纤维膜的力学性能

王敏超1，熊 杰1，2

(1.浙江理工大学材料与纺织学院，浙江 杭州 310018;2.浙江理工大学先进纺织材料与制备技术教育部重点实验室，浙江 杭州 310018)

对静电纺丝素蛋白(SF)/聚己内酯(PCL)复合纳米纤维膜在拉伸速率比为1∶1、2∶1、5∶1、8∶1下进行双轴向拉伸破坏实验和在拉伸速率比为1∶1、2∶1、4∶1、5∶1、8∶1下进行双轴向循环拉伸实验。结果表明，静电纺纳米纤维膜拉伸断裂负荷与施加的拉伸速率比有关，静电纺纳米纤维膜在循环载荷作用下具有非线性非弹性的特性。对双轴向循环拉伸负荷与伸长率曲线进行拟合，建立了静电纺纳米纤维膜在双轴向循环拉伸加载段的数学模型。以拉伸速率比为4∶1的循环拉伸曲线为例，运用该数学模型所得曲线与实验曲线比较一致，证实模型有效。

静电纺纳米纤维膜;力学性能;双轴向拉伸实验;数学模型

静电纺丝技术制备的纤维膜具有孔隙率高、比表面积大等特点，可较好地模拟细胞外基质的结构，使其在组织工程领域有很大的使用价值［1－2］，在生物医学领域具有乐观的应用前景［3－4］，然而静电纺膜材料在实际应用中多向受力，其力学性能非常复杂，为实现其在临床医学等方面的深入应用，研究静电纺纤维膜在复杂受力环境下的力学性能有着重要的现实意义。

Urszula 等［5－6］利用单轴拉伸仪测试了静电纺PA6纤维膜的力学性能，但此方法只能表征纤维膜在单一受力方向上的力学性能，具有较大局限性。利用双轴拉伸仪测试材料的力学性能已见报道。Mari等［7］对经编弹性针织物进行双轴向拉伸测试，并建立了有关纱线张力、纱线线密度与拉伸变形量之间的理论方程，经验证，理论计算所得数据与实验数据较为符合。Shang等［8］研究了混凝土在动态双轴向拉伸压缩载荷下的力学性能，结果表明，试样拉伸强度和压缩应变随施加载荷的增大而减小。Joseph等［9］比较了管状猪颈动脉和平面猪颈动脉的双轴拉伸力学性能发现，在同等载荷条件下，平面试样具有较大的拉伸应力，胶原蛋白的取向排列使管状试样的双轴向拉伸力学性能表现为各向异性。然而目前双轴向拉伸力学性能研究主要集中在织物、建筑材料及生物材料领域，针对静电纺纳米纤维膜的双轴向拉伸力学性能研究却不多见。

本文将静电纺丝素蛋白/聚己内酯复合纳米纤维膜在4种拉伸速率比下进行双轴向拉伸破坏实验，分析静电纺纳米纤维膜两向的拉伸断裂负荷与施加拉伸速率比的关系;在5种拉伸速率比下对静电纺纤维膜进行双轴向3次循环拉伸实验，使静电纺纳米纤维膜的力学性能在经过循环作用后更接近实际使用情况，并根据第2次循环拉伸曲线建立数学模型［10－12］，对第 3 次循环拉伸实验数据进行验证，以拉伸速率比为4∶1的循环拉伸段曲线为例，模型拟合数据与实验数据较为符合。本文期望为建立静电纺纳米纤维膜的双轴向力学本构模型提供参考。

1 实验部分

1.1 材料与仪器

再生丝素蛋白(SF)，自制;聚己内酯(PCL，80000)，深圳光华伟业有限公司;六氟异丙醇(HFIP)，纯度＞99%，盐城冬阳生物制品有限公司;FC60P2型高压电源，美国Glassman公司;KDS100型微量注射泵，美国KDS Scientific股份有限公司。

1.2 静电纺丝

将SF与PCL按质量比为25∶75溶于HFIP中，配成质量分数为6%的溶液，于磁力搅拌器中搅拌12 h，得到透明纺丝溶液。静电纺丝参数为:外加静电场电压15 kV，纺丝流率0.6 mL/h，距离接收平板12cm。所得静电纺SF/PCL纳米纤维膜置于真空干燥箱中静置备用。

1.3 静电纺纳米纤维膜双轴向拉伸性能测试

采用日本加多(KATO)公司KSM-BX5450ST型双向拉伸试验仪对静电纺纳米纤维膜进行双轴拉伸，实验装置如图1所示。试样尺寸为60mm×60mm，夹持距离为50mm，X向、Y向拉伸量程均为5 N。双轴拉伸破坏实验中，X向与Y向的拉伸速率比分别为1∶1、2∶1、5∶1和 8∶1;双轴 3 次循环拉伸实验中，X向比 Y向的拉伸速率比分别为 1∶1、2∶1、4∶1、5∶1和8∶1，变形量为10mm。

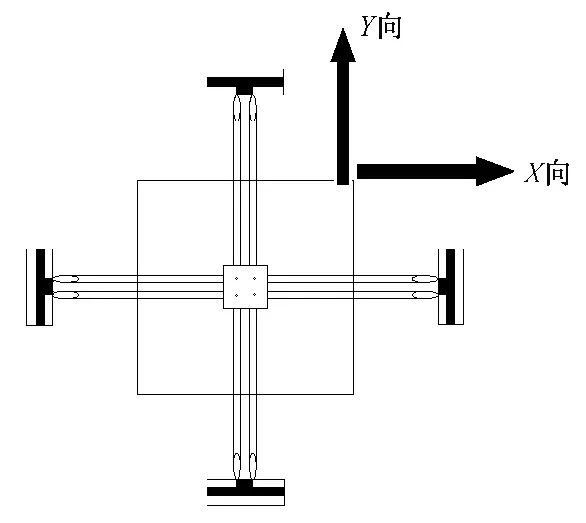
图1 KSM-BX5450ST型双向拉伸试验仪测试示意图Fig.1 Schema of KSM-BX5450ST compact biaxial tensile tester

2 结果与讨论

2.1 双轴拉伸破坏测试

表1示出双轴拉伸断裂负荷(最大拉伸负荷)。图2示出试样在4种不同拉伸速率比值下的X向及Y向拉伸负荷与伸长率曲线。

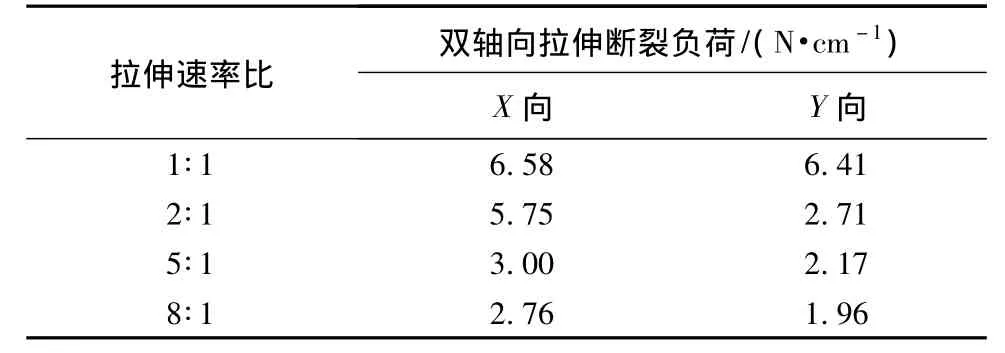
表1 静电纺SF/PCL纳米纤维膜双轴向拉伸断裂负荷Tab.1 Biaxial tensile breaking load of electrospun SF/PCL nanofibrous membranes

图2 静电纺SF/PCL纳米纤维膜在不同拉伸速率比下的双轴拉伸负荷与伸长率曲线Fig.2 Biaxial tensile loading-stretch rate curves of electrospun SF/PCL nanofibrous membranes under different tensile rate ratios

从表中可看出，当两向加载速率相同时，试样两向拉伸断裂负荷均较高。随着X与Y向拉伸速率比增大，X向拉伸断裂负荷高于Y向，但两向拉伸断裂负荷并不呈现与施加拉伸速率比相应的比值关系。拉伸速率比增大，试样X向拉伸断裂负荷呈减小趋势，但没有呈现相应的比值关系，拉伸断裂伸长率(最大拉伸伸长率)差别不大;当拉伸速率比大于2∶1时，Y向拉伸断裂强度减小程度并不明显。

2.2 双轴向循环拉伸测试

图3、4分别示出试样在5种不同拉伸速率比下循环拉伸时的X向及Y向拉伸负荷与伸长率曲线。从图中可看出，静电纺纳米纤维膜的双轴向拉伸重要特征，非线性及非弹性:1)非线性，拉伸负荷和伸长率之间为非线性关系，其非线性程度和拉伸次数有关。循环拉伸次数越多，拉伸负荷与伸长率越趋于线性关系;2)非弹性，静电纺纳米纤维膜在循环拉伸作用下，拉伸段与回复段曲线不重合，存在残余应变。随着拉伸次数增加，残余应变减小，拉伸段曲线与回复段曲线越接近。

从图中还可看出，静电纺纳米纤维膜除上述非线性、非弹性外，在不同拉伸速率比的双轴向拉伸实验中还表现出以下特点:随着X向与Y向拉伸速率比值增大，两向的最大拉伸负荷均减小;当拉伸速率比大于2∶1时，最大拉伸负荷减小程度并不明显，这与双轴拉伸破坏实验结果相似。

2.3 双轴向拉伸曲线拟合

为进一步分析施加不同拉伸速率比时，静电纺纳米纤维膜在周期性载荷作用下拉伸负荷与伸长率曲线的变化规律，本文重点研究曲线的加载段，并根据加载段曲线变化的基本趋势，用二次方程进行回归拟合:

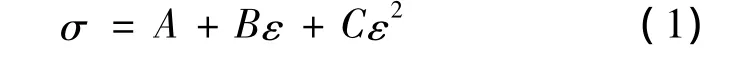
式中:σ为拉伸负荷;ε为伸长率;A、B、C为回归系数。

以X向为例，图5示出第2个循环拉伸加载段回归系数A、B、C随拉伸速率变化的趋势曲线，并用指数函数进行拟合。从图中各回归系数的变化趋势可见，随着拉伸速率比增大，回归系数A有增大的趋势，而B、C则呈减小的趋势。

对A、B、C的变化曲线进行拟合，可用式(2)描述第2个循环的拉伸段A、B、C与拉伸速率比R之间的关系［11－12］:

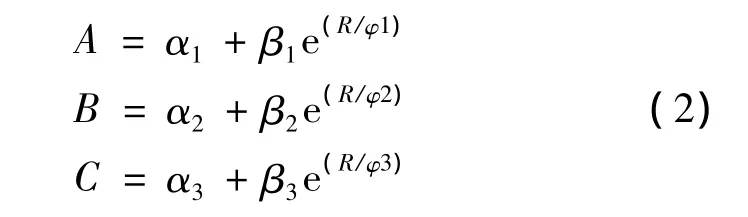
式中，α、β、φ是用指数函数拟合曲线的系数，如表2所示。

于是可得，试样第2次循环的拉伸段有

表2 拟合曲线系数α、β、φTab.2 Coefficient of fitting curve

因此，静电纺SF/PCL纳米纤维膜在双轴向拉伸作用下，X向的拉伸负荷与伸长率关系模型可由下式描述:

以拉伸速率比4∶1的曲线为例，运用该数学模型对第3次拉伸段数据进行验证，得到拉伸负荷与伸长率曲线b，与实验曲线a进行比较，如图6所示。理论曲线b与实验曲线a趋势一致，数值相差较小，可认为式(1)、(2)的假设较为合理。

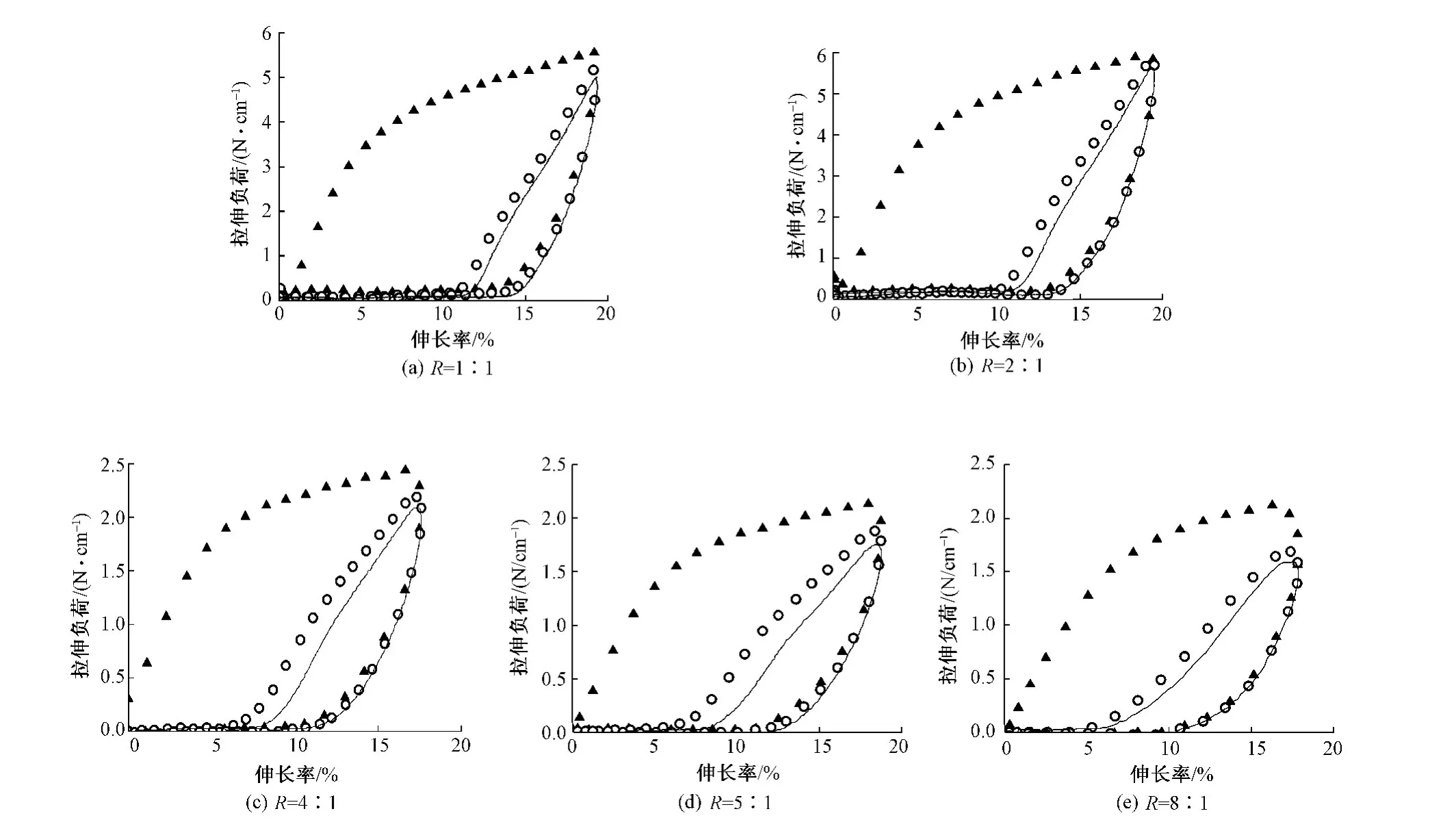
图3 不同拉伸速率比下SF/PCL纳米纤维膜的X向循环拉伸负荷与伸长率曲线Fig.3 X axial cyclic tensile loading-stretch rate curves of SF/PCL nanofibrous membranes under different tensile rate ratios

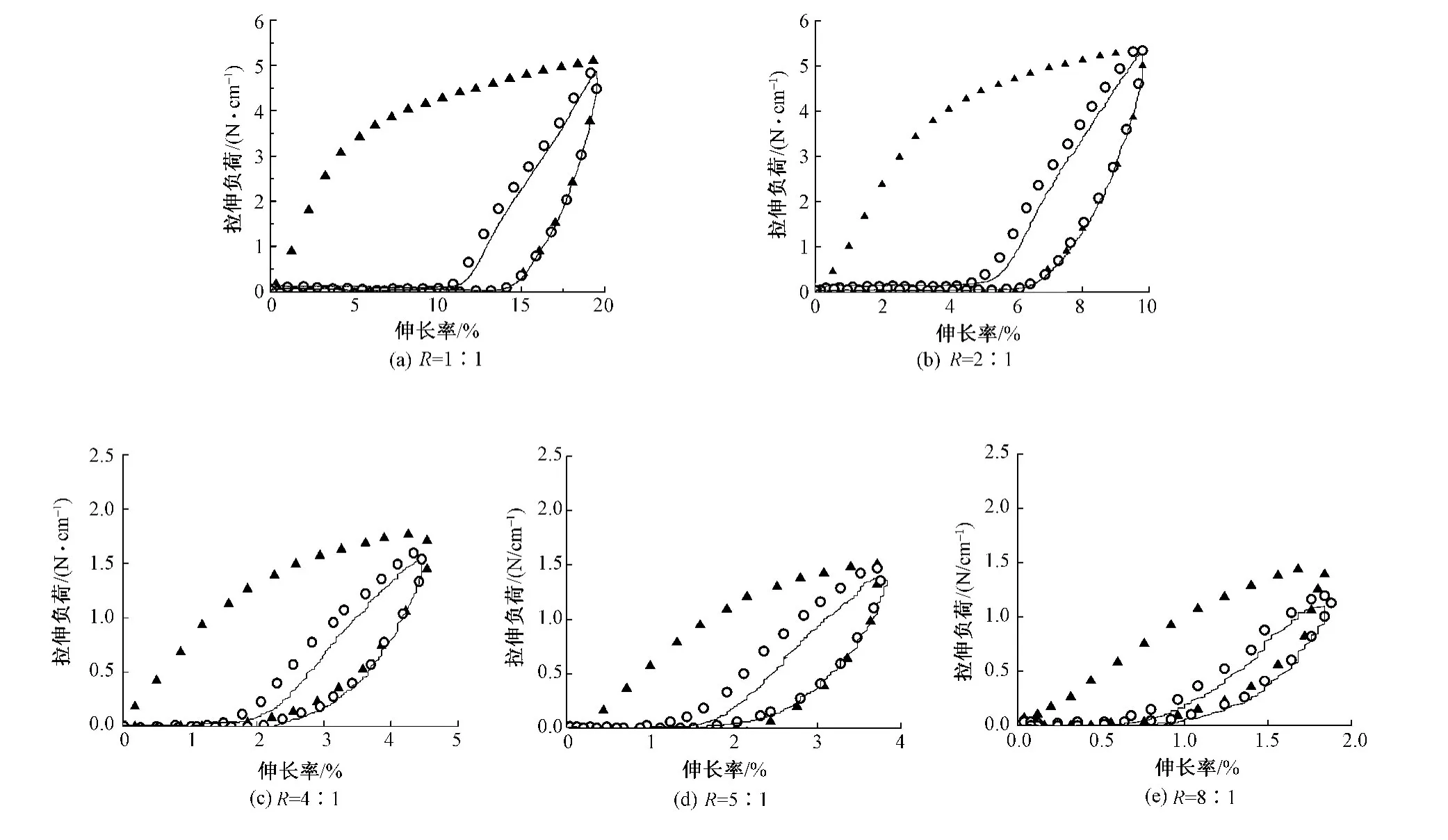
图4 不同拉伸速率比下SF/PCL纳米纤维膜的Y向循环拉伸负荷与伸长率曲线Fig.4 Y axial cyclic tensile loading-stretch rate curves of SF/PCL nanofibrous membranes under different tensile rate ratios

图5 静电纺SF/PCL纳米纤维膜X轴向第2次循环拉伸的回归系数A、B、C与拉伸速率比R的关系Fig.5 Relationship between tensile rates ratio(R)and regression coefficient(A，B，C)of electrospun SF/PCL nanofibrous membranes on second drawing

图6 静电纺SF/PCL纳米纤维膜在拉伸速率比为4∶1下双轴向第3次循环拉伸段拉伸负荷与伸长率曲线Fig.6 Biaxial cyclic tensile loading-stretch rate curves of electrospun SF/PCL nanofibrous membranes under tensile rate ratio of 4∶1

3 结论

1)通过不同拉伸速率比的双轴向拉伸破坏实验可知，当X向与Y向施加拉伸速率比为1∶1时，静电纺纳米纤维膜两向均具有最大的拉伸断裂负荷，且大小几乎相等。

2)在双轴向循环载荷作用下，静电纺纳米纤维膜具有非线性、非弹性的力学性能。多次循环后，非线性与非弹性程度降低。

3)在双轴向循环载荷作用下，随着X向比Y向拉伸速率比增大，两向的拉伸负荷均随之减小，当拉伸速率比大于2∶1时，静电纺纳米纤维膜拉伸负荷随拉伸速率比变化并不明显。

4)对双轴向循环拉伸曲线进行拟合，建立了数学模型σ=A+Bε+Cε2。以拉伸速率比为4∶1的循环拉伸曲线为例，对实验数据进行验证，结果表明运用该数学模型所得曲线与实验曲线比较一致，证明模型有效。

［1］ 王群旺，许淑燕，熊杰，等.混杂聚丁二酸丁二醇酯调控再生丝素蛋白超细纤维膜的力学性能［J］.纺织学报，2011，32(6):18－21.WANG Qunwang，XU Shuyan，XIONG Jie，et al.Adjustment and control of mechanical properties of silk fibroin ultrafine fibrous membrane by hybrid electrospinning with PBS ［J］.Journal of Textile Research，2011，32(6):18－21.

［2］ HYE Sung Kim，HYUK Sang Yoo.In vitro and in vivo epidermal growth factor gene therapy for diabetic ulcers with electrospun fibrous meshes［J］. Acta Biomaterialia，2013，9(7):7371－7380.

［3］ LEE S J，LIU J，OH S H，et al.Development of a composite vascular scaffolding system that with stands physiological vascular conditions［J］. Biomaterials，2008，29:2891－2898.

［4］ ZHANG Y H，VENU Gopal J R，El-Turki A，et al.Electrospun biomimetic nanocomposite nanofibersof hydroxyapatite/chitosan for bone tissue engineering［J］.Biomaterials，2009，29:4314－4322.

［5］ URSZULA Stachewicz，ILKER Peker，WEI Tu，et al.Stress delocalization in crack tolerantelectrospun nanofiber networks［J］.Applied Materials Interfaces，2011(3):1991－1996.

［6］ LIN Jiantao， LI Caihong， ZHAO Yi， et al. Coelectrospun nanofibrous membranes of collagen and zein for wound healing［J］.Applied Materials Interfaces，2012(4):1050－1057.

［7］ MARIInoue， AYAKO Tange， MASAKO Niwa.Theoretical analysis of biaxial tensile properties of power net［J］.Textile Research Journal，2013，83(12):1319－1324.

［8］ SHANG Shiming， SONG Yupu. Dynamicbiaxial tensile-compressive strength and failure criterion of plain concrete［J］.Construction and Building Materials，2013，40:322－329.

［9］ JOSEPH T Keyes， DANIELLE R Lockwood，URS Utzinger， et al. Comparisons of planar and tubular biaxial tensile testing protocols of the same porcine coronary arteries［J］. Annals of Biomedical Engineering，2013，41(7):1579－1591.

［10］ MICHAE S Sacks.Biaxial mechanical evaluation of Planar biological materials［J］.Journal of Elasticity，2000，61:199－246.

［11］ 倪静，罗仁安，陈有亮，等.建筑膜材料在双轴拉伸作用下的特性［J］.工程力学，2009，26(6):100－104.NI Jing， LUO Ren'an， CHEN Youliang， et al.Characteristics of architectural membrane materials under biaxial tensile loads［J］.Engineering Mechanics，2009，26(6):100－104.

［12］ KAGEYAMA M， KAWABATA S，NIWA M.The validity of a linearizing method for predicting the biaxial extension properties of fabrics［J］.Journal of The Textile Institute，1988(79):543－565.

Mechanical properties of electrospun silk fibroin/poly(ε-caprolactone)nanofibrous membranes under biaxial tensile loads with different tensile rates

WANG Minchao1，XIONG Jie1，2
(1.College of Materials and Textiles，Zhejiang Sci-Tech University，Hangzhou，Zhejiang 310018，China;2.Key Lab of Advanced Textile Materials and Manufacturing Technology of Ministry of Education，Zhejiang Sci-Tech University，Hangzhou，Zhejiang 310018，China)

Biaxial tensile tests of electrospun silk fibroin(SF)/poly(ε-caprolactone)(PCL)composite nanofibrous membranes were done in this paper.The biaxial tensile failure experiment was carried out under tensile rate ratios of 1∶1，2∶1，5∶1，8∶1，and the biaxial cyclic tensile experiment were carried out under tensile rate ratios of 1∶1，2∶1，4∶1，5∶1，8∶1.The results indicate that the tensile breaking load of electrospun composite nanofibrous membranes is closely related to the tensile rate ratios，and the biaxial tensile mechanical properties under cyclic loads are nonlinear and inelastic.In this paper，mathematical model describing the relationship between tensile loading and stretch rate during biaxial cyclic tensile testing was established through fitting the experimental curve，and it was applied to biaxial cyclic tensile testing under tensile rate ratio of 4∶1.The consistence of the modeling and experimental curves verifies that the mathematical model is effective.

electrospun nanofibrous membrane;mechanical property;biaxialtensile test;mathematical model

TQ 342.9

A

10.13475/j.fzxb.201506001806

2013－10－15

2014－12－08

国家自然科学基金资助项目(11272289)

王敏超(1989—)，女，硕士生。主要研究方向为静电纺纳米纤维。熊杰，通信作者，E-mail:jxiong@zstu.edu.cn。