四维变分同化技术在风暴潮数值模拟中的应用
王宗辰,于福江,2,原野,2(.国家海洋环境预报中心,北京0008;2.国家海洋局海洋灾害预报技术研究重点实验室,北京0008)
四维变分同化技术在风暴潮数值模拟中的应用
王宗辰1,于福江1,2,原野1,2
(1.国家海洋环境预报中心,北京100081;2.国家海洋局海洋灾害预报技术研究重点实验室,北京100081)
摘要:利用区域海洋模式ROMS(Regional Ocean Modelling System)及其四维变分同化模块,建立了具有资料同化能力的东中国海风暴潮数值模式,通过将海洋站水位观测资料同化到风暴潮模式中,提高了模式对风暴潮的模拟精度。四维变分同化技术能够在整个同化时间窗口保持动力协调,使模拟结果在该时间窗口内最大程度的靠近观测,同时,得到了最优预报初始场。利用该模式,对两次温带风暴潮过程进行了数值模拟,结果表明:在同化窗口内,同化对模拟精度有明显的提高;结束同化之后,得到的最优预报初始场对临近预报精度也有一定提高。
关键词:区域海洋模式ROMS;四维变分同化;风暴潮数值模拟;最优预报初始场
1 引言
目前风暴潮数值预报结果多是由确定性数值模式计算得到,但是采用确定性风暴潮数值模式,有时模拟结果和实际情况相比仍然有较大的误差[1]。这些误差的来源主要包括3个方面:一是动力模式对真实物理过程的各种近似处理,例如模式物理参数化过程;二是大气风应力和模式开边界等输入资料的不确定性;三是由数值计算方法引起的误差。解决这一问题比较有效的方法之一是将风暴潮数值模式和宝贵的观测资料通过最优的方法融合起来,发展具有同化能力的数值模式。近年来,各种同化方法在风暴潮预报领域开展了较为广泛的应用[1-10],其中比较有代表性的是Kalman滤波在西北欧国家风暴潮业务化中的应用[2-4],和变分同化在参数估计、状态估计中的应用[6-9]。
Kalman滤波方法的缺点是对观测资料序列有严格限制,即观测资料不能出现缺测,并且要求资料序列必须是等时间间隔[1]。本文所采用的四维变分同化算法突破了这些限制,在个别站点缺测或者资料序列时间间隔不等的情况下,模式仍可以顺利运行得到结果。Sasaki[11]第一次提出了满足控制方程强约束条件的伴随方法,完成了四维变分同化的基本理论。20世纪末,伴随方法被引入到气象数据分析和同化领域[12],之后,又被引入到全球海洋状态分析和海洋环流模式中。Zhang等[6-7]通过将模式得到的“伪观测数据”(包括余水位和近岸潮汐,余水位指总水位减去潮汐)同化到二维POM(Princeton Ocean Model)中,估计了风拖曳系数和侧边界的潮汐等。Peng等[8-9]在台风风暴潮研究中应用四维变分同化技术,将“伪观测数据”(由高分辨率模式产生)同化到模式中,对台风风暴潮进行了后报试验,结果表明只同化水位就可以有效的改进预报结果。但遗憾的是,超过同化的3 h窗口,模式结果的改进大概只能持续5 h左右,这也是由台风风暴潮的特点决定的,其风场变化剧烈,增水速度快,持续时间短,一般在6 h到12 h之间。本文则选取了温带风暴潮作为试验对象,主要考虑其风场变化相对缓慢,增减水的时间尺度更长,可以持续12 h到36 h,这样,同化窗口可以设置得更宽,最优预报初始场就可以包含更多的水位信息。
本文选择ROMS作为水动力模式,第一个原因是其具备模拟风暴潮的能力。韩国气象厅的You等[13]通过3次影响韩国的台风风暴潮过程对ROMS在西北太平洋的应用进行了检验,模拟表明ROMS的预报结果和韩国现有的风暴潮预报系统(RTSM, Regional Tide/Storm Model)结果相当,而且有更大的空间变化,以后很有可能用ROMS取代现有的业务化预报系统;美国马里兰大学的Li等[14]和爱尔兰气象中心的Wang等[15]也都利用ROMS分别对发生在切萨皮克湾和爱尔兰附近的风暴潮过程进行了模拟,结果令人满意。另一个重要原因是其四维变分同化技术的有效性已被验证,Powell等[16-17]和Broquet等[18-20]在北美边缘海开展了一系列基于ROMS的四维变分同化研究,取得了不错的效果。
本文基于ROMS建立了具有资料同化能力的东中国海风暴潮数值模式,并进行了温带风暴潮个例试验。文章接下来介绍模式的基本配置,然后简要说明强约束增量型四维变分同化的算法及其实现,最后分析试验结果并加以总结和讨论。
2 模式配置
ROMS是近10年来新发展起来并被广泛认可的一个三维、自由海面和基于地形跟随坐标的非线性斜压原始方程模式,具体可参考文献[21-23]。
本文选取的模拟区域为114.233°—133°E,22.2°—41°N,包含渤海、黄海、东海以及西日本海和西北太平洋海域,水平网格分辨率为(1/10)°× (1/10)°,格点数为188×189,垂直方向分为20层,这样的分辨率设置既可以较好的刻画风暴潮过程又能够兼顾计算效率。
水深资料来自英国海洋资料中心(BODC, British Oceanographic Data Centre)的格点数据gebco_08(0.5′×0.5′),同时,近岸水深(h<100 m)由国家海洋环境预报中心业务化水深数据(2′×2′)插值代替,最小水深5 m,最大水深约为6000 m(见图1)。岸线数据采用美国地球物理资料中心(NGDC, National Geophysical Data Center)最高分辨率的GSHHG-2.2.2数据。南、东、北三个方向设为开边界,二维平均流速采用Flather边界条件,即正压模态的偏差以重力外波的速度(传播出去;与之配合,水位采用Chapman边界条件,即水位以浅水波速(播出去;三维流速采用辐射边界条件。
ROMS的大气强迫方式有2种方法可供选择,因风暴潮过程在近岸主要受风强迫影响,所以只采用风应力作为外强迫,风应力由欧洲中长期天气预报中心的再分析风场(ERA-Interim)根据Large & Pond[24]的公式计算得到,空间分辨率0.75°×0.75°,时间分辨率3 h,内模积分时间步长取180 s,外模取9 s。
3 四维变分同化算法和实现
3.1四维变分同化算法
资料同化的过程是将确定性模式结果和观测数据融合在一起,生成一个对海洋状态的重新估计,这种估计应该比确定性模式结果更加接近真值。四维变分同化技术通过动力约束使模式结果与观测之间距离达到最小化,动力协调一致是这种技术的优点;缺点是通过迭代的方法求解伴随方程解的过程非常消耗计算资源,虽然可以通过具体的迭代次数来控制计算时间,但实际情况是,为了保证目标函数的收敛,状态变量的维数不宜太大,这也是水平网格选择(1/10)°×(1/10)°的主要原因。
ROMS自带的四维变分同化技术由Courtier[25]首先提出,现已在业务化数值天气预报模式中展开了广泛的应用,下面简单介绍其原理和方法。
根据贝叶斯理论,得到有观测条件下“最优初始场”(或称“分析场”)的条件概率(表达式略);再根据最大似然估计推出,若要使概率最大,则下面的表达式(目标函数)取极小值,即
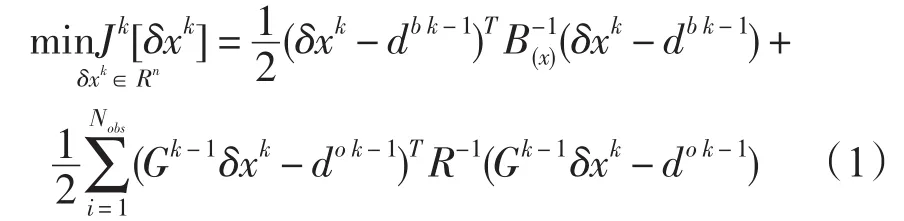
式中,δxk=xk-xk-1、db k-1=xb-xk-1、do k-1= yo(i)-G(xk-1);x∈Rn表示控制变量;n代表控制变量的空间维数;xb∈Rn表示背景场估计值;δxk表示外循环的迭代增量;k代表外循环次数;yo(i)∈Rm表示观测值;i代表观测值的时间维数;m代表观测值的空间维数;Gk-1是一个Rn→Rm的线性空间映射算子,用来实现切线性模式的向前积分和模式结果向观测空间线性插值;B(x)∈Rn×n和R∈Rm×m分别代表背景误差协方差和观测误差协方差的估计值,都是对称正定矩阵。
另外循环次数为1,则k=1,一般的x0=xb,目标函数简化为:

对简化了的目标函数求导得:

使其等于0便可得到δx的解析解,但很遗憾,目前只能通过迭代算法使目标函数向某一点收敛,ROMS所采用的是基于Lanczos方法的共轭梯度下降算法[26-28]。
3.1.1背景误差协方差
到目前为止,如何准确的构造背景误差协方差仍是一个非常具有挑战性的问题,原因是无法获得真值,同时又缺乏足够的样本资料。本文参照“NMC”方法[29],选取12个不同时效的预报值对背景误差进行估计。具体做法是,从12个不同的时刻冷启动模式,然后获得同一时刻后报结果作为样本,把样本的平均值看做“真值”,12个样本离差的平均值近似的看做背景误差,背景误差协方差可以表达为
3.1.2观测误差协方差
考虑到风暴潮过程的时空尺度,海洋站的水位数据是一种比较理想的同化资料。因此,选取了中国沿海24个海洋站的逐时水位数据作为同化资料。为了简化问题,本文不考虑潮汐以及潮汐和风增水的非线性相互作用,因此选择T_TIDE[30]作为调和分析的工具,对24个海洋站的水位进行调和分析。利用调和分析的结果推算潮汐,总水位减去潮汐,就得到了风暴潮,风暴潮误差统一设定为0.02 m,假定R是一个对角矩阵,则R对角线上所有元素均为0.0004 m2。
3.2算法实现
设定同化窗口[t0,t1],外循环设为1层,内循环10层。根据本文的试验结果,这样的设置可以保证目标函数基本收敛。
(1)从t0开始热启动非线性模式,向前积分到t1,得到[t0,t1]时刻内的背景场xb,其中ℕ表示非线性模式的转移矩阵,f表示大气强迫;
(2)从t0时刻开始,选择一个δx(δx≪xb),向前积分切线性模式到t1时刻,得到t1时刻的Gδx-d和J,其中ℂ(t)=∂ℕ/∂x|xb;
(3)再从t1时刻开始,用R-1(Gδx-d)强迫伴随模式向后积分到t0时刻,根据公式(3)可以得到∂J/∂δx;
(4)选择共轭梯度下降算法不断更新δx;
(5)重复步骤2—4,直到满足收敛条件,即得到最优初始场xb+δx。
4 数值模拟和结果
本文选择了2011年初发生在渤海的两次温带风暴潮过程作为试验对象,分别是1月15日0时—1 月16日24时(世界时,后同)的一次减水过程和2月26日0时—2月27日24时一次增水过程,两次过程的持续时间大约都为48 h,为了观察后续变化,模式运行的结束时间向后延长12 h。这两次风暴潮的影响范围仅限于渤海区域,因此,虽然同化了24个海洋站水位资料,但每次过程只选出渤海区域风暴潮位最大的4个海洋站作为分析对象。
4.1减水个例
4.1.1试验设计
控制试验(CR):风暴潮过程开始前48 h,冷启动模式运行至风暴潮过程结束;
同化试验1(DA1):控制试验运行48 h后,加入同化模块,同化时间窗口设为向后12 h,然后停止同化,运行至风暴潮过程结束;
同化试验2(DA2):控制试验运行48 h后,加入同化模块,同化时间窗口设为向后24 h,然后停止同化,运行至风暴潮过程结束;
同化试验3(DA3):控制试验运行48 h后,加入同化模块,同化时间窗口设为向后36 h,然后停止同化,运行至风暴潮过程结束。
4.1.2结果分析
控制试验和3个同化试验模拟结果与观测水位的时间序列如图2所示。可以看出,控制试验和同化试验都较好的模拟出了风暴减水的趋势,同化试验的模拟结果明显优于控制试验。在0—48 h期间,同化试验3的模拟结果和观测最为接近,这表明36 h的同化窗口最为准确的模拟出了本次风暴减水过程。

图2 1月15日0时—1月17日12时,4个海洋站的风暴减水时间序列(0时是同化窗口的起始时刻,有色虚线表示对应颜色同化试验的同化结束时刻)
同化试验3可以看做一个再分析过程,其模拟结果可以近似认为是真值。计算了同化试验3和控制试验在减水过程中不同时刻模拟结果的绝对差值,其空间分布见图3。可以看出,不同时刻的大值区分布不尽相同,但差值比较大的区域主要分布在靠近湾顶或近岸处,这表明确定性模式的预报水位绝对误差在靠近湾顶或海湾处比较大。
对于风暴潮数值预报,同化的目的是要得到一个比确定性模式更为接近实际的预报初始场,从而提高确定性模式的预报精度[1]。同化试验1同化了12 h的模拟结果可以看做最优预报初始场,为了定量描述其对预报结果的改进,定义水位改进度为
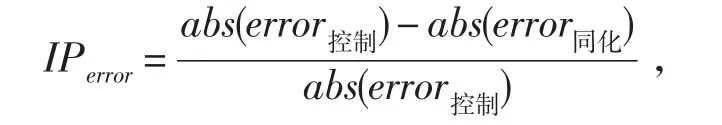
式中,error表示误差;abs表示绝对值算符。
利用同化试验1得到的最优预报初始场对水位进行预报,并计算了逐时的水位改进度(见图4),同时,设定当改进度不小于30%时,最优预报初始场对预报精度有显著地提高。可以看到,对于这次风暴减水过程,从初始时刻同化12 h之后得到的最优预报初始场,不同程度的提高了4个海洋站的预报精度,不同站点的改进时长在15—17 h之间,但对于芝罘岛预报水位改进度偏低的现象,原因不详。同时可以看到,4站的改进度曲线存在不同程度的波动,龙口和芝罘岛表现得尤其明显,这和图2中水位曲线的波动是对应出现的,可能是因为站点水位里包含了和模式不兼容的物理过程,引起了模式的不稳定。

图3 同化试验3与控制试验水位差绝对值的空间分布(单位:cm)
4.2增水个例
4.2.1试验设计
控制试验(CR):风暴潮过程开始前48 h,冷启动模式运行至风暴潮过程结束;
同化试验1(DA1):控制试验运行60 h后,加入同化模块,同化时间窗口设为向后6 h,然后停止同化,运行至风暴潮过程结束;
同化试验2(DA2):控制试验运行60 h后,加入同化模块,同化时间窗口设为向后12 h,然后停止同化,运行至风暴潮过程结束;
同化试验3(DA3):控制试验运行60 h后,加入同化模块,同化时间窗口设为向后24 h,然后停止同化,运行至风暴潮过程结束。
4.2.2结果分析
控制试验和3个同化试验模拟结果与观测水位的时间序列如图5所示。可以看出,控制试验和同化试验都较好的模拟出了增水趋势,控制试验极大值点附近出现了较大误差,其中黄骅站极值误差达到了70 cm,极值的相位也存在1—4 h的滞后。3个同化试验对极值水位的预报精度都有提高,同化试验3的模拟结果和观测最为接近,黄骅站的最大增水误差减少了约30 cm,对极值点位相的订正也非常明显。

图4 同化试验1中4个海洋站预报结果的逐时水位改进度(虚线代表30%的改进度)
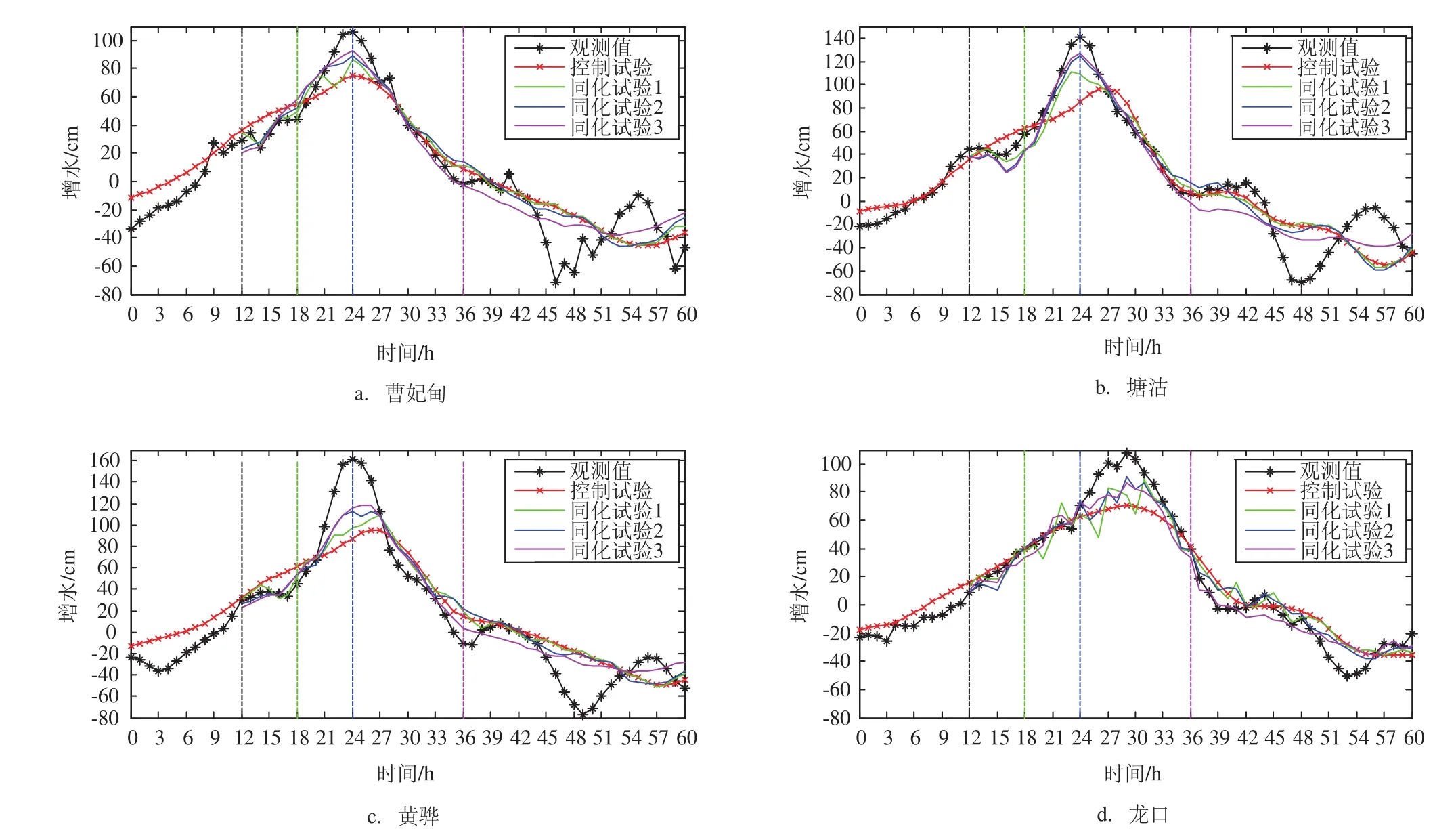
图5 2月26日0时—2月28日12时,4个海洋站风暴增水时间序列(黑色虚线表示同化窗口的起始时刻,其他有色虚线表示对应颜色同化试验的同化结束时刻)
同化试验3同样可以看做一个再分析过程,其模拟结果可以近似认为是真值。计算了同化试验3和控制试验在4个临近增水极大值时刻模拟结果的绝对差值,其空间分布见图6。分析结果与减水试验相似,不再赘述。

图6 同化试验3与控制试验水位差绝对值的空间分布(单位:cm)
同化试验1在6时的模拟结果作为最优预报初始场,对水位进行了预报。对于风暴增水过程,我们更加关注增水的极值和极值出现的时间,因此根据观测选择了每个站点增水极大值出现时刻前后各3 h共7 h的预报结果进行分析,表1列出了同化试验1中这7 h的逐时水位改进度。从表中可以看到,大部分时刻的预报精度都有所提高,但同时,曹妃甸和龙口两站的改进度出现了一些负值和小值,这和图5中两站水位曲线波动现象是对应的,可能是因为站点水位里包含了和模式不兼容的物理过程,引起了模式的不稳定。把同化试验2在12时的模拟结果作为最优预报初始场,对水位进行了预报,结果显示预报改进度有进一步提高,显然是因为预报初始场更加靠近增水极值时刻。

表1 同化试验1在4个海洋站增水极值时刻前后3 h的逐时水位改进度(单位:%)
5 总结和讨论
本文利用ROMS及其强约束增量型四维变分同化模块建立了中国渤、黄、东海风暴潮数值预报模式,通过将观测余水位同化到模式中,改进了同化窗口内的风暴潮数值模拟结果。同时,资料同化技术可以提供更为合理的预报初始场,对风暴潮的临近预报结果有一定改进。对于风暴减水过程,30%的预报水位改进可以持续约15—17 h;对于风暴增水过程,预报结果的改进程度和最优预报初始场时刻有关,其越接近增水极值时刻,对风暴增水预报结果的改进越大。
目前,国家海洋环境预报中心的温带风暴潮业务化预报每天运行两次,分别是7时和15时,发布预报时间为8时和16时。以7时开始运行为例,模式所采用的同化资料只能是7时之前的海洋站数据,风速为预报中心业务化风场预报结果,这就要求模式要在1 h之内运行结束。根据本文的试验结果,24 h的预报结果5 min便可计算得到,同化及预报共计需要约50 min,可以满足8时发报的要求。实际上,预报中心可以实时接收海洋站数据,只要风场在预报时效内,风暴潮模式随时可以运行。
风暴潮过程基本可以看做一个外强迫问题,即初始场只在前期对预报结果影响比较大,随着时间推移,风强迫的作用变得更加重要。本文的一个隐含假设是风应力等其他资料是准确的,模式也是准确的,仅海洋的初始状态存在误差,但实际情况是,即便通过同化技术订正了初始场,预报结果和观测相比仍存在系统性误差。因此,在模式没有改动的情况下,可以认为风应力、近岸地形和水深是误差主要来源,通过资料同化技术更加合理的估计风应力是下一步的研究方向。
致谢:本文所用海洋站资料均来自国家海洋环境预报中心信息室,在此表示感谢!
参考文献:
[1]于福江,张占海,林一骅.一个稳态Kalman滤波风暴潮数值预报模式[J].海洋学报, 2002, 24(5): 26-35.
[2] Heemink A W. Storm surge prediction using Kalman filtering[D]. Twente: Twente University of Technology, 1986.
[3] Heemink A W, Mouthaan E E A, Roest M R T, et al. Inverse 3D shallow water flow modeling of the continental shelf [J]. Continental Shelf Research, 2002, 22(3): 465-484.
[4] Sorensen J V T, Madsen H. Efficient Kalman filter techniques for the assimilation of tide gauge data in three-dimensional modeling of the North Sea and Baltic Sea system[J]. Journal of Geophysical Research, 2004, 109(C3), doi: 10.1029/2003JC002144.
[5] Butler T, Altaf M U, Dawson C, et al. Data Assimilation within the Advanced Circulation (ADCIRC) Modeling Framework for Hurricane Storm Surge Forecasting[J]. Monthly Weather Review, 2012, 140(7): 2215-2231.
[6] Zhang A J, Parker B B, Wei E. Assimilation of water level data into a coastal hydrodynamic model by an adjoint optimal technique[J]. Continental Shelf Research, 2002, 22(14): 1909-1934.
[7] Zhang A, Wei E, Parker B B. Optimal estimation of tidal open boundary conditions using predicted tides and adjoint data assimilation technique[J]. Continental Shelf Research, 2003, 23 (11-13): 1055-1070.
[8] Peng S Q, Xie L. Effect of determining initial conditions by four-dimensional variational data assimilation on storm surge forecasting[J]. Ocean Modelling, 2006, 14(1-2): 1-18.
[9] Peng S Q, Xie L, Pietrafesa L J. Correcting the errors in the initial conditions and wind stress in storm surge simulation using an adjoint optimal technique[J]. Ocean Modelling, 2007, 18(3-4): 175-193.
[10] Lionello P, Sanna A, Elvini E, et al. A data assimilation procedure for operational prediction of storm surge in the northern Adriatic Sea[J]. Continental Shelf Research, 2006, 26(4): 539-553.
[11] Sasaki Y. Some basic formalisms in numerical variational analysis [J]. Monthly Weather Review, 1970, 98(12): 875-883.
[12] Le Dimet F X, Talagrand O. Variational algorithms for analysis and assimilation of meteorological observations: theoretical aspects[J]. Tellus A, 1986, 38(2): 97-110.
[13] You S H, Lee W-J, Moon K S. Comparison of storm surge tide predictions between a 2Doperational forecasting system operational forecast system, RTSMand ROMS[J]. Ocean Dynamics, 2010, 60(2): 443-459.
[14] Li M, Zhong L J, Boicourt W C, et al. Hurricane-induced storm surges, currents and destratification in a semi-enclosed bay[J]. Geophysical Research Letters, 2006, 33(2): L02604. doi: 10.1029/ 2005GL024992
[15] Wang S Y, McGrath R, Hanafin J, et al. The impact of climate change on storm surges over Irish waters[J]. Ocean Modelling, 2008, 25(1-2): 83-94.
[16] Powell B S, Arango H G, Moore A M, et al. 4DVAR data assimilation in the Intra-Americas Sea with the Regional Ocean Modeling System (ROMS)[J]. Ocean Modelling, 2008, 25(3-4): 130-145.
[17] Powell B S, Moore A M. Estimating the 4DVAR analysis error of GODAE products[J]. Ocean Dynamics, 2009, 59(1): 121-138.
[18] Broquet G, Edwards C A, Moore A M, et al. Application of 4D-variational data assimilation to the California Current System [J]. Dynamics of Atmospheres and Oceans, 2009, 48(1-3): 69-92.
[19] Broquet G, Moore A M, Arango H G, et al. Ocean state and surface forcing correction using the ROMS-IS4DVAR data assimilation system[J]. Mercator Ocean Quarterly Newsletter, 2009, 34: 5-13.
[20] Broquet G, Moore A M, Arango H G, et al. Corrections to ocean surface forcing in the California Current Systemusing 4D-variational data assimilation[J]. Ocean Modelling, 2011, 36 (1-2): 116-132.
[21] Shchepetkin A F, McWilliams J C. A method for computinghorizontal pressure-gradient force in an oceanic model with a nonaligned vertical grid[J]. Journal of Geophysical Research, 2003, 108(C3), doi: 10.1029/2001JC001047
[22] Shchepetkin A F, McWilliams J C. The regional oceanic modeling system (ROMS): a split explicit, free-surface, topographyfollowing-coordinate oceanic model [J]. Ocean Modelling, 2005, 9 (4): 347-404.
[23] Haidvogel D B, Arango H, Budgell W P, et al. Ocean forecasting in terrain-following coordinates: formulation and skill assessment of the Regional Ocean Modeling System[J]. Journal of Computational Physics, 2008, 227(7): 3595-3624.
[24] Large W G, Pond S. Open ocean momentum flux measurements inmoderatetostrongwinds[J]. Journal of Physical Oceanography, 1981, 11(3): 324-336.
[25] Courtier P, Thépaut J-N, Hollingsworth A. A strategy for operational implementation of 4D-Var, using an incremental approach[J]. Quarterly Journal of the Royal Meteorological Society, 1994, 120(519): 1367-1387.
[26] Fisher M. Minimization algorithms for variational data assimilation[R]//Proceedings of ECMWF Seminar Recent Developments in Numerical Methods for Atmospheric Modelling. U.K.: ECMWF Publication, 1998, 364-385.
[27] Tshimanga J. On a class of limited memory preconditioners for large-scalenonlinearleast-squaresproblems[D]. Namur, Belgium: Facultes Universitaires Notre-Dame de la Paix, 2007.
[28] Tshimanga J, Gratton S, Weaver A T, et al. Limited-memory preconditioners with application to incremental variational data assimilation[J]. Quarterly Journal of the Royal Meteorological Society, 2008, 134(632): 751-769.
[29] Parrish D F, Derber J C. The national meteorological center's spectral statistical-interpolation analysis system[J]. Monthly Weather Review, 1992, 120(8): 1747-1763.
[30] Pawlowicz R, Beardsley B, Lentz S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE[J]. Computers and Geosciences, 2002, 28(8): 929-937.
Application of four-dimensional variational data assimilation technique in storm surge simulations
WANG Zong-chen1,YU Fu-jiang1,2,YUAN Ye1,2
(1. National Marine Environmental Forecasting Center, Beijing 100081 China; 2. Key Laboratory of Research on Marine Hazards Forecasting, State Oceanic Administration, Beijing 100081 China)
Abstract:Base on Regional Ocean Modeling System(ROMS) with four-dimensional variational (4D-Var) data assimilation modules, a model is established for storm surge simulation in the East China Sea, and the deterministic model output is corrected by assimilating the available tidal gauge station data. The 4D-Var technique is able to compensate for the errors between modeled outputs and observations by containing dynamically consistent and persistent during a period of time(also called assimilation window), and the optimal initial condition for forecasting is obtained. Two applications on extra tropical storm surges that occurred in Bohai are performed by the model. The results show that the procedure is capable of strongly improving simulation accuracy, and the optimal initial condition effectively improves the forecasting accuracy in a short period.
Key words:Regional Ocean Modeling System (ROMS); 4D-Var data assimilation; storm surge simulation; optimal initial conditions
作者简介:王宗辰(1988-),男,硕士研究生,主要从事风暴潮数值模拟及同化技术研究。E-mail:781004920@163.com
基金项目:海洋公益性行业专项(200905013)
收稿日期:2014-01-06
DOI:10.11737/j.issn.1003-0239.2015.01.001
中图分类号:P731.23
文献标识码:A
文章编号:1003-0239(2015)01-0001-09

