井筒空间内以CO2为载热流体的多相流流动算法分析*
石 岩
(吉林建筑大学市政与环境工程学院,长春 130118)
井筒空间内以CO2为载热流体的多相流流动算法分析*
石岩
(吉林建筑大学市政与环境工程学院,长春130118)
摘要:在地热开采井井筒空间内流体的流速计算通常采用动量守恒方程,而对于多相流系统直接求解动量方程比较困难,同时也很难将井筒流和储层流模型耦合在一起.为了解决这一问题,通过介绍引入漂移流模型DFM(Drift Flux Model)的方法,将多相流系统不同相的流速建立关系,从而将动量守恒方程中多个未知数转为一个未知数,实现多相流动量守恒方程各参数的求解.
关键词:漂移流模型;动量守恒;多相流
深部地热资源开发过程中,井筒(水平、垂直或倾斜)是地表和地下热储层发生物质和能量交换的主要通道.由于井筒流动空间大、表面光滑等特征,流体在其中的流动与在多孔介质中截然不同,不再满足达西定律,而是满足更为普遍的动量守恒定律,而如何实现动量守恒方程的求解是计算井筒空间内流体流速的关键问题.
1质量和能量守恒方程
1.1 累积项Mκ的计算
首先假设井筒具有圆形的一维线性特征,井内流体的流态为紊流,流体的能量运移及转换除了考虑传导和对流以外,增加考虑了动能和势能的影响和相互转化,同时考虑井筒内流体与周围介质的热量交换过程.井筒中的流体的流速计算采用的是动量守恒方程,在多相流流动系统中,直接求解动量方程比较困难,同时也很难和储层的模型耦合在一起.为了解决这个困难,引入漂移流模型DFM(Drift Flux Model)[1-2],将多相系统中不同相的流速建立关系,进而把动量守恒方程中的多个未知数转为一个未知数,实现动量守恒方程的求解.在完成动量守恒方程求解后,再利用DFM获得每个相的流速,统一求解储层和井筒的多相流动、热传导及对流方程.
根据质量和能量守恒原理,广义的井筒质量和能量守恒方程如下:
(1)
式中,κ为组份指数:κ=1表示水,κ=2表示CO2,κ=3表示能量(包含动能和内能);Mκ为组份κ的累积项;qκ为质量或能量的源(汇)项;Fκ为平流过程井筒内质量和能量的运移项.
单相或两相系统中对于质量组份(水和CO2)公式(1)的累积相Mκ计算公式如下:

(2)
式中,Xβκ为β相κ组份的质量分数(β=G表示气相,β=L表示液相);ρβ为β相的密度;Sβ为β相的局部饱和度,计算公式如下:
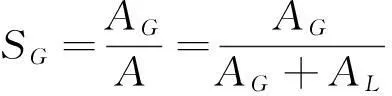
(3)
式中,A为井筒的横截面积,m2;AG和AL分别为被气相和液相占据的给定高度(或井的高程)的横断面积,m2.
累积相的能量方程为:

(4)
1.2 流动项Fκ的计算
流体沿着井筒的运移是通过对流、扩散和弥散等方式实现.κ组份的对流通量被定义为:

(5)
式中,uβ为井筒内的平均速度矢量,m/s;A为井筒的横截面积,m2;z为沿井筒的坐标(可以是垂直的,也可以是倾斜或水平的),m.
井筒内流体能量的运移包括对流换热、动能、势能以及流体与侧边界的热损失.一维能量运移项可以如下表示:

(6)
式中,hβ为流体β相的比焓,J/kg;g为重力加速度,Pa/m;θ为井筒的倾斜角度,°;q″为单位长度井筒的得(失)热量(当井筒及围岩构造不确定时是可选项),W;ρ为气-液混合密度,kg/m3;λ为井筒截面积上的平均导热系数,W/(m·℃);T为温度,℃.
为简化计算过程,上述公式省略了井筒与周围构造的质量或能量的交换.
井筒与围岩之间的热量交换通过两种方式计算:
(1) 如果存在围岩网格,可以通过TOUGH2中的流体通过孔隙介质的导热及对流公式计算,如将网格节点到井筒侧面接口的距离设置为零时此项功能即取消;
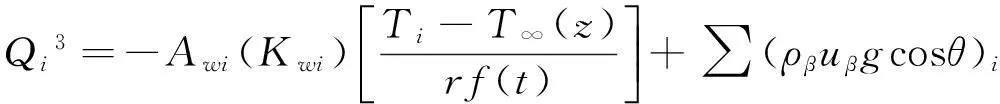
(7)
其中,Qi3既包括井筒侧壁面的传热量,也包括势能的转化(摩擦损失被转化成热,因此不会影响整体的能量平衡).式中,Awi为井筒与围岩间的侧面积,m2;Kwi为井筒与围岩间的传热系数,W/m2·K;Ti表示井筒第i个网格的温度,℃;T∞(z)表示周围环境的温度,℃;r表示井筒的半径,m;f(t)表示Ramey井流热损失.
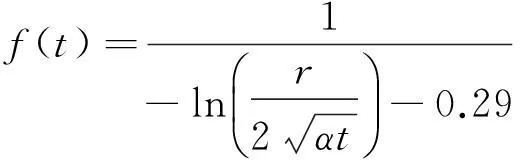
(8)
其中,α是围岩的热扩散系数.
2漂移流模型(DFM)的动量守恒方程
2.1 不同助剂对胶粘剂粘结强度、耐水性、凝胶时间的影响
孔隙介质中的流动其流量或流速可以通过达西定律的压力和重力梯度进行简化计算,但井筒内的流速是通过求解动量守恒方程得到的.直接求解与储层模拟器耦合的两相流体动量方程比较困难,因此,我们通过调用DFM模型描述井筒内单相和多相流动,从而获得对流传输项(质量或能量流量Fβ与流速uβ).
漂移流模型最早由Zuber,Findlay及Wallis提出[1-2],其基本理论是将气相速度uG、液相速度uL用体积流量j、系数C0及漂移速度ud来表达.

(9)
式中,C0为形状参数,影响井筒横断面的局部气体饱和度和速度.由定义,体积流量j为体积加权的平均速度:
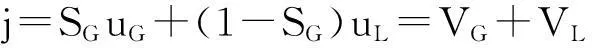
(10)
因此,液相流速uL可以定义为:

(11)
漂移流模型公式(9)~(11),井筒两相流的动量方程可以简化成混合流速um和漂移流速ud的单相方程.漂移流模型中所涉及的所有变量除明确指出,否则均被认为是井筒截面的面积平均值或是常数.
忽略井筒轴向应力时,井筒多相流动量守恒方程如下[3]:
2016年企业研发投入的参数β2=7.41,即在其他条件不变的情况下,研发费用每增加1万元,主营业务利润增加7.41万元。P值为0.058,在10%的显著性水平下,表明2016年的企业研发投入对于2017年的主营业务利润有显著影响。
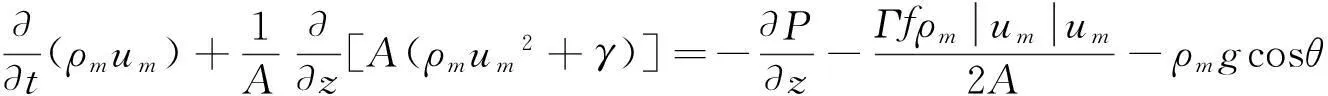
(12)
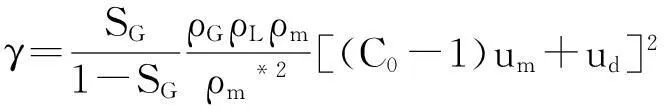
混合密度ρm和um定义如下:

(13)

(14)
受形状影响的平均密度ρm*定义如下:

(15)
因此,通过采用DFM方法,使复杂的两相动量方程简化成两个步骤:
(1) 通过求解简化的动量方程(12)获得混合流速um,以及通过经验关系获得漂移流速ud;
(2) 再通过下式计算气体流速和液体流速:

(16)
不同界面上的两相流相互作用,形成不同的流动机制,因此如何准确计算漂移流速ud及形状参数C0是DFM的难点.不同流动机制C0和ud关系函数是不同的.依据Shi等提出的形状参数和漂移流速的功能表,C0与ud是通过大量广泛的管道流实验获得的[4].这些实验是Oddie等在多种条件下针对单相、两相和三相流体流动所做的,并被连续应用到所有流动机制[5].TOUGH2Bore中采用的漂移流速数学公式是由Shi等提出[4].首先,通过气体饱和度和其他流体性质计算漂移流速,公式如下:
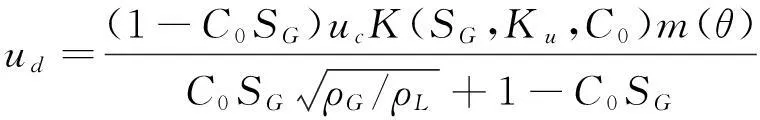
(17)
式中,m(θ)被描述为m(θ)=m0(cosθ)n1(1+sinθ)n2.其中m0,n1和n2是安装参数;Ku是库塔杰拉兹(Kutateladze)数,为邦德数NB的函数(井径的无量纲数的平方):

(18)
式中,Cw是壁面摩擦因素(在代码被取为固定数0.008),邦德数NB定义如下:

(19)
式中,d是井筒直径,参照图1相同文献的实验数据,Cku在TOUGH2Bore中取为142.
其中,特征流速uc是液体沸腾上升流速的测量值,计算公式如下:

(20)
式中,σGL是气相和液相之间的表面张力.
公式(17)中K的功能是使漂移流速在沸腾上升阶段和浸水层流阶段形成一个平稳过渡.不同于Shi等线性插入方法,我们使用下面的功能:
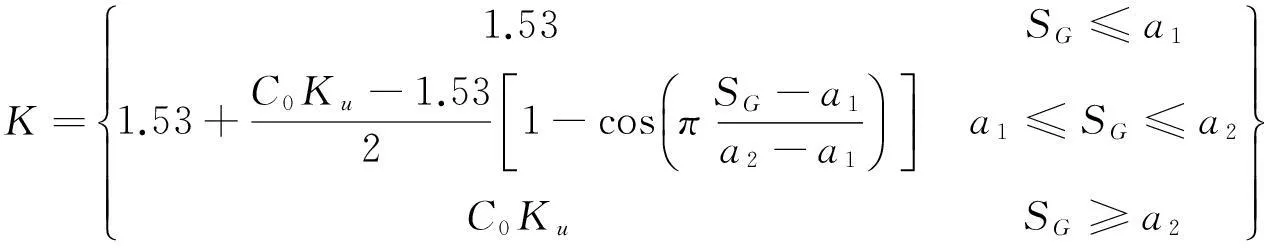
(21)
这里a1和a2是Shi等[4]提出的气体饱和度的两个转换点.当SG≥a2和SG≤a1时,K不依赖气体饱和度;当a1≤SG≤a2时,K的功能通过dK/dSG=0搭建起来,使导数在整个区间均连续.对于拟合参数m0,n1,n2,a1和a2的赋值来自Shi等中水/气实例,其值取决于Cmax(一个用户指定的最大形状参数介于1.0和1.5之间),如表1所示.

表1 TOUGH2Bore 中DFM的经验参数[4]
形状参数Cmax通过下式进行计算[4]:
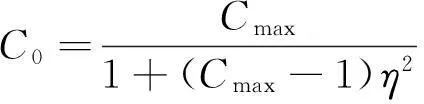
(22)
这里η是反映形状参数对流动状态影响的参数,计算公式如下:

(23)
式中,B是高于C0低于Cmax的极限参数.β的计算公式如下:
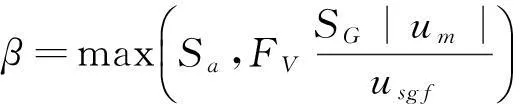
(24)
与文献[4]中所述略有不同的是,我们使用的极限参数B是由Cmax决定:

(25)
式中提供当Cmax=1.2时,B=0.6,这与文献[4]中a1(=0.06)和a2(=0.12)的计算值是一致的.B的变化区间由Cmax=1.0时的0.933 3到Cmax=1.5时的0.266 6.需注意的是:如果Cmax=1.0,C0将不受气体饱和度或流速的限制,形状影响消失.
形状平的或多或少对气相流速的影响可以通过调整公式(24)的FV(默认值=1),因此usgf可以通过下式计算:

(26)
3结语
本文通过介绍在井筒空间内引入漂移流模型DFM(Drift Flux Model)的方法,将多相流动量守恒方程中多个未知数转化为一个未知数,从而获得不同相流速的求解方法,实现了井筒空间内以CO2为载热流体的多相流动量守恒方程参数求解.
参考文献
[1] Zuber N,Findlay JA.Average volumetric concentration in two-phase flow systems[J].J Heat Transfer ASME,1965,87(4):453-468.
[2] Wallis.One-Dimension Two Phase Flow[M].New York,1969:10-54.
[3] Brennen,CE.Fundamentals of multiphase flows[M].Cambridge:Cambridge University Press,2009:34-35.
[4] Shi H,Holmes JA,Durlofsky LJ,Aziz K,Diaz LR,Alkaya B,Oddie G.Drift-flux modeling of two-phase flow in wellbores[J].Soc Pet Eng J,2005,10(1):24-33.
[5] Oddie G,Shi H,Durofsky LJ,Aziz K,Pfeffer B,Holmes JA.Experimental study of two and three phase flows in large diameter inclined pipes[J].International Journal of Multiphase Flow,2003,29(4):527-558.
Algorithm Analysis of the Flow on Multi-phase Fluid in
Wellbore with CO2as the Heat Transfer Fluid
SHI Yan
(SchoolofMunicipalandEnvironmentalEngineering,JilinJianzhuUniversity,Changchun,China130118)
Abstract:In a multiphase flow system,the flowrate of wellbore fluid is calculated according to the momentum conservation equation.It is difficult to directly solve the momentum equation,and it is also difficult to couple with the reservoir model together.In order to solve this problem,the drift flow model (DFM)is conductied to build a relationship of the flow rate of the different phases in the multiphase system,and then many of the in the momentuconservation equation is converted to one unknown parameter,so it can be to realize the solution of the momentum conservation equation. After completion of the momentum conservation equations,the each phase velocity is can be get by using DFM.
Keywords:drift flux model;conservation of momentum;multi-phase fluid
*基金项目:吉林省科技厅科技计划项目(20130522070JH);吉林省教育厅“十二五”科学技术研究项目(吉教科合字[2014]第239号).
作者简介:石岩(1977~),女, 吉林省长春市人,副教授,博士.
收稿日期:2014-10-10.
中图分类号:TB 302.2
文献标志码:A
文章编号:2095-8919(2015)03-0031-05

