基于Runge-Kutta法的高压电缆导体温度计算

徐 研

(广州供电局有限公司,广州 510310)

基于Runge-Kutta法的高压电缆导体温度计算

徐 研

(广州供电局有限公司,广州 510310)

为了解决电缆导体温度不能直接准确测量和电缆敷设环境给导体温度准确计算带来困难的问题,通过实时监测电缆表面温度,建立了电缆导体温度实时计算热路模型,采用Runge-Kutta法求解微分方程组计算出导体温度。通过搭建电缆温升实验平台,对比计算结果与实验结果得知,基于表面温度的监测实时计算电缆导体温度具有较高的精度,能满足运行中电缆的状态监测和故障预警等方面的需求。

电力电缆;温度;Runge-Kutta法;试验

随着城市中高压线路的不断建设与投运,供电系统所用电缆逐渐演变为以高压电缆为主,这样就对电缆线路安全可靠性的要求也逐渐提高[1]。电缆导体温度是电缆安全运行的重要参数,电缆线芯发热会使电缆出现故障甚至发生火灾,因此实现对线芯温度的监控是必要的。文献[2]根据传热学原理,建立基于电缆表面温度来计算线芯温度的热路模型,实现了电缆线芯稳态温度计算。文献[3-4]引入有限元法以及有限差分法等数值计算方法,为电缆温度场分析提供了方便,但其对电缆线芯实时暂态计算研究较少。前述这几种计算方法都是利用IEC 60287中提供的相关公式与参数,由外部环境反推出电缆线芯温度,其计算结果与实际运行工程误差较大,不能满足要求。本文根据热路与电路的相似性,建立了单芯高压电缆热路模型,利用在线监测系统测得的电缆表面温度与负荷电流以及电缆结构参数作为计算条件,实现了电缆各层温度的精确计算。

1 热路模型的建立与分析

通过理论计算电缆温度场可知,将表面温度、实时负荷以及电缆结构参数作为已知条件,在敷设环境未知的情况下,可以精确计算出电缆缆芯实时温度[5-7]。

在建立电缆热路模型时,必须确定电缆的传热模型具有单值性[8],单值性条件包括:

1) 几何条件。给出导热过程中的物体大小和形状。如果各向是同性质的材料,还应给出主轴方向的导热系数。

2) 物理条件。确定物质之间各种关系的物性量值,例如有无内热源的大小和分布情况,及随温度变化的函数关系等。

3) 时间条件。描述导热过程在时间上的特点,即对于稳定状态过程不需要时间条件;而对于非稳定状态过程,则要给出初始温度分布状况。

4) 边界条件。表述在区域边界上导热发展过程的特点。

根据以上条件,将单芯高压电缆视为几何中心圆结构,考虑绝缘层介质损耗、铝护套环流损耗以及各层热阻热容作用情况,可以建立电缆的热路模型,如图1所示。

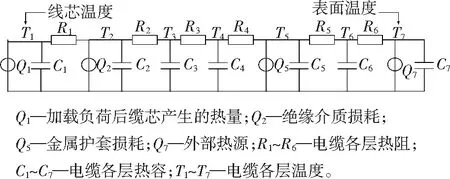
图1 电缆热路模型

根据热路工作原理,通过热路模型计算的电缆温度为

(1)

(2)

(3)

(4)

(5)

(6)

由式(1)～(6)可知,计算电缆温度的方程组是由一阶微分方程组成,可以简写成矩阵形式:

T=At+BQ

其中

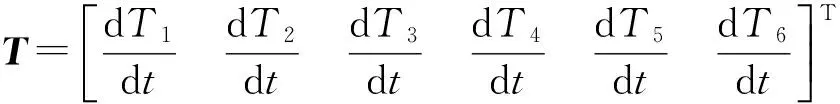
2 四阶经典Runge-Kutta法

由于直接求解一阶微分矩阵方程的解析解工作量很大,求解的精度也不能满足要求。因此本文利用四阶Runge-Kutta法,求出微分矩阵方程的解,且其精度满足工程需要。

在求解微分方程组时可以考虑微分:

dx=f(t，x，y)dt

dy=g(t，x，y)dt

可得出微分方程组:

四阶龙格库塔公式为

虽然循环肿瘤细胞、循环肿瘤DNA和microRNA、外泌体等新兴血液生物标志物检测因其无创性和低风险性逐渐兴起，但其临床应用仍然相对较少[10]，而血清肿瘤标志物仍然是胰腺癌中应用最为广泛的生物标志物[11]。

(7)

其中

(8)

式(8)是关于x和y的递推公式,其中h是关于时间的步长。计算f和g后代入式(7)中就可得到tk+1时刻数值解xk+1和yk+1。因此利用Runge-Kutta法对公式求解,可得到t时刻T1～T2的值,即电缆各层温度分布状况。

3 试验验证

3.1 试验装置

为准确掌握电缆温度的实际变化情况,验证理论计算的准确性和环境因素对该算法的影响[9],设计了不同敷设条件的电缆负荷温升试验。试验装置如图2所示,其主要由五部分组成:试验电源、调压器、大电流发生器、试验测量设备和试验电缆。试验电缆选用YJLW02 127/220 1×2000和YJLW02 64/110 1×630两种电压等级电缆,电缆分别采用4 m顶管敷设、1 m水中敷设和空气中敷设,电缆敷设前将测温热电偶设置于测温点,用于监测电缆各个位置温度变化情况。

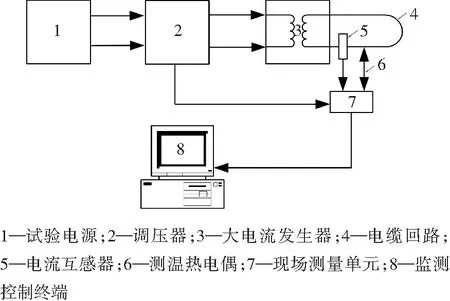
图2 电缆温升试验装置接线原理图

3.2 试验结果与对比分析

3.2.1 顶管敷设试验

3.2.2 水中敷设试验

对在水中敷设的630 mm2电缆施加650 A电流正常运行后,增加到电流1300 A 12 h后,阶跃电流到1500 A 2 h,再降为满负荷1300 A。模拟电缆线路在满负荷时需要短时负荷运行情况,其导体温度的实测值与计算值的对比曲线如图4所示。

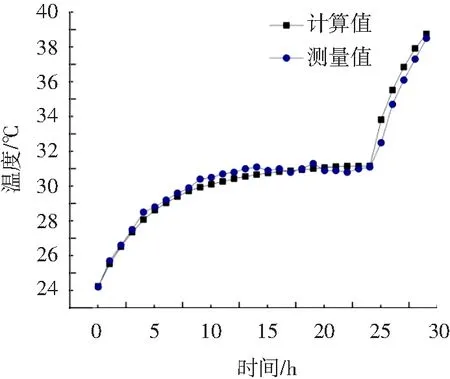
图3 埋深4 m敷设电缆导体温度实测与计算比较

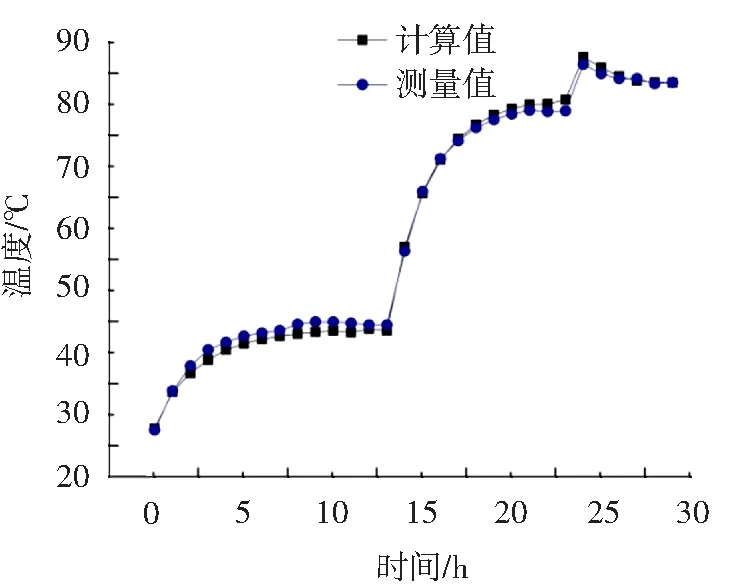
图4 水中敷设电缆导体温度实测与计算比较

由图4可以看出,在水中敷设的电缆计算与试验最大相差温度为1.8 ℃,证明了实时导体计算模型与算法在任何环境下可以使用。

3.2.3 空气中敷设试验

对在空气中敷设的630 mm2电缆施加动态负荷电流,其导体温度的实测值与计算值的对比曲线如图5所示。

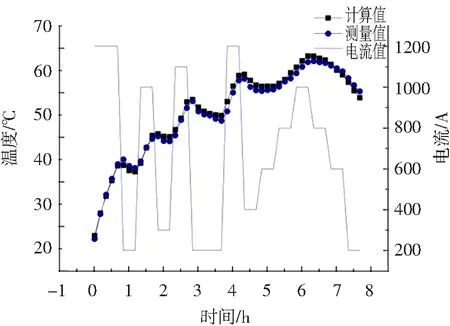
图5 空气中敷设电缆导体温度实测与计算

从图5可以看出,实时导体计算模型与算法在负荷改变的情况下,依然具有较高的计算精度,最大相差温度为1.5 ℃。

4 结 语

本文根据热路模型建立了电缆导体温度实时计算模型,采用Runge-Kutta法求解模型所得到的微分方程组,利用电缆表面温度及实时负荷计算导体温度,避免了电缆由于敷设环境复杂而带来的计算误差。依据环境不同的计算结果与试验结果对比,证明了该算法的准确性与高效性。另外,可利用该方法实时监测电缆运行状态,当导体温度过高时,进行故障预警。

[1] 赵健康,雷清泉,王晓兵,等.复杂运行条件下交联电缆载流量研究[J].高电压技术,2009,35(12):3123-3128. ZHAO Jiankang, LEI Qingquan, WANG Xiaobing, et al. Experimental research on ampacity of extruded power cable under complex operating condition [J]. High Voltage Engineering,2009,35(12):3123-3128.

[2] 刘毅刚,罗俊华. 电缆导体温度实时计算的数学方法[J].高电压技术, 2005,31(5):52-54. LIU Yigang,LUO Junhua. Mathematical method of temperature calculation of power cable conductor in real time [J]. High Voltage Engineer,2005,31(5): 52-54.

[3] DE LEON F,ANDERS G J. Effect s of back filling on cable ampacity analyzed with the finite element method [J]. IEEE Trans on Power Delivery, 2008, 23(2):537-543.

[4] 梁永春,柴进爱,李彦明,等. 基于FEM的直埋电缆载流量与外部环境关系的计算[J]. 电工电能新技术, 2007, 26(4): 10-13. LIANG Yong chun, CAI Jinai, LI Yanming, et al. Alculation of ampaciy reduction factors for buried cables with surroundings based on FEM [J]. Advanced Technology of Elecrical Engineering and Energy, 2007,26(4):10-13.

[5] 罗俊华,周作春,李华春,等.电力电缆线路运行温度在线检测技术应用研究[J].高电压技术,2007, 33(1):169-172. LUO Junhua, ZHOU Zuochun, LI Huachun,et al. Application of operation temperature detection technique for on-line power cable lines [J]. High Voltage Engineering, 2007, 33(1):169-172.

[6] 彭超,赵健康,苗付贵,等.分布式光纤测温技术在线监测电缆温度[J].高电压技术,2006,32(8):43-45. PENG Chao,ZHAO Jiankang, MIAO Fugui, et al. Distribut-ed temperature system applied in cable temperature measureme-nt [J]. High Voltage Engineering, 2006, 32(8): 43-45.

[7] 楼开宏,秦一涛,施才华,等.基于光纤测温的电缆过热在线监测及预警系统[J].电力系统自动化,2005,29(19): 97-99. LOU Kaihong,QIN Yitao, SHI Caihua, et al. On-line monitoring and early warning system of cable overheating based on optical fiber temperature measurement[J].Automation of Electric Power Systems, 2005, 29(19): 97-99.

[8] 杨世铭,陶文铨.传热学[M].北京:高等教育出版社,2006. YANG Shiming, TAO Wenquan. Heat transfer[M]. Beijing: Higher Education Press, 2006.

[9] HANNA M A,CHIKHANI A Y,SALAMA M M A.Thermal analysis of power cables in multi-layered soil-Part 1:Theoretical mod-el[J].IEEE Trans on Power Delivery,1993,8(3):761-771.

(责任编辑 郭金光)

Calculation of HV cables core’s temperature based on Runge-Kutta method

XU Yan

(Guangzhou Power Supply Bureau Co.,Ltd,Guangzhou 510310,China)

To solve the problems of cable core’s temperature calculation,including the indirect measure ment and the influence of cable laying environment on the temperature,this paper established the real time thermal circuit model of cable core’s temperature based on the real-time monitoring of cable surface temperature,and calculated the core temperture by solving differential equations with Runge-Kutta method.By comparing the results of calculation and experiment through the established cable temperature rise platform,it is proved that the the temperature calculation based on the real-time monitoring of surface temperature enjoys higher accuracy,which meets the requirements for state monitoring and fault early warning.

power cable;temperature;Runge-Kutta method;test

2015-04-21。

徐 研(1985—),男,硕士,工程师,主要从事电力电缆运行管理维护工作。

TM247

A

2095-6843(2015)06-0543-04