无缝钢管张力减径张力系数的理论计算与分析

李金锁，吕庆功

（1.天津冶金集团中兴盛达钢业有限公司，天津 301616；2.北京科技大学高等工程师学院，北京 100083）

张力减径机是现代化的生产机组，可以实现钢管的增壁厚、等壁厚和减壁厚变形，在热轧无缝钢管生产过程中得到广泛使用［1-2］。一般的减径机上单机架减径量只有3%～5%，而张力减径机的单机架减径量可达7%（甚至更高），总减径量可达85%，总减壁量可达38%［3-4］。因此，张力减径机前面的轧管机可以只生产少数几种规格的荒管，通过张力减径机来得到各种规格的成品管，从而大大提高热轧无缝钢管机组的生产效率、扩大产品规格范围［5-6］。

张力系数是控制钢管壁厚变化的关键参数，其设定和控制水平对于成品钢管的壁厚精度具有重要的影响［7］。通常情况下，张力减径机应尽可能采用大的张力系数，以强化张力减径工序的减壁变形能力，但必须结合具体工艺条件进行合理设定。一般张力减径的张力系数为0.34～0.50时为等壁减径，张力系数为0～0.33时为增壁减径，张力系数大于0.50时为减壁减径，实际生产中的最大张力系数可取到0.65～0.85［8-10］。临界张力系数是钢管在张力减径变形时壁厚由增厚转为减薄时的张力系数值，也即钢管在张力减径变形时发生等壁变形的张力系数值，是合理设定张力系数的重要参考值。

本文从理论上分析了张力系数对无缝钢管张力减径变形的影响特点，进而分析临界张力系数的影响因素和变化特点，最后通过生产应用实例验证了所述张力系数选择方法的实用性和有效性。

1 钢管张力减径塑性方程式推导

在钢管张力减径变形区的横截面上取一微单元体，如图1所示。

图1 钢管张力减径变形区横截面微单元体示意

根据图1建立径向力的平衡方程式如下：

略去高阶小量后可得：

将式（2）两侧积分后可得：

式（3）中C为常数，可以利用钢管内表面的边界条件求得。钢管内表面的径向应力为零，即r=D/2-S，σr=0，代入式（3）可求得常数C为：

将式（4）代入式（3）可得径向应力σr与切向应力σt的关系为：

令壁厚系数γ=1-（D-2S）/（2r），则：

根据最大剪应力理论［11-12］，轴向应力σl与切向应力σt有如下关系：

式中k——金属的剪切屈服应力。

由张力系数Z的定义可得其表达式：

另外，根据塑性变形理论的基本假设条件［13］，应力与对数变形的关系式为：

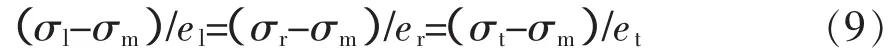
式中el，er，et——钢管的轴向、径向、切向对数变形；

σm—— 平均应力，σm=（σl+σr+σt）/3。

将式（6）～（8）及 σm的表达式代入式（9）可得：

式（10）即为钢管张力减径的塑性方程式，它反映了钢管轴向、径向和切向应变与钢管壁厚系数及张力系数之间的解析关系。

为简化分析，假设变形区内各处的应力状态都与壁厚中间层上的应力状态相同，即r=（D-S）/2，则γ=S/（D-S），代入式（10）可得：

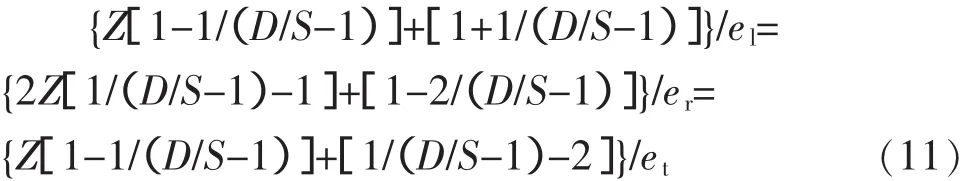
令 Φl=Z［1-1/（D/S-1）］+［1+1/（D/S-1）］，Φr=2Z［1/（D/S-1）-1］+［1-2/（D/S-1）］，Φt=Z［1-1/（D/S-1）］+［1/（D/S-1）-2］。Φl、Φr、Φt的大小即代表了钢管在轴向、径向和切向的变形，正值表示增大，负值表示减小，0表示保持不变。可以看出：张力减径时金属在轴向、径向和切向的流动分配只与张力系数Z和钢管的径壁比D/S有关。在不同的D/S情况下，张力系数对三向变形的影响程度不同。

2 张力系数对钢管张力减径变形的影响

在D/S分别等于5、10、15、20、25、30的情况下，作Φl、Φr、Φt与张力系数Z的关系曲线，如图2所示。

由图2可以看出：①Φl、Φr、Φt与张力系数Z基本呈线性关系；②Φl始终为正值，随着Z增大而增大，说明增大张力系数有利于促进钢管的纵向延伸变形；③Φt始终为负值，也随着Z增大而增大，说明增大张力系数不利于钢管的减径变形；④Φr随Z增大由正值变为负值，其斜率约是前两者的2倍，说明增大张力系数有利于钢管的减壁变形，而且对壁厚变化的影响比较突出；⑤当张力系数Z小于临界张力系数Zl时，Φl和Φr为正，Φt为负，说明钢管在周向被挤压的金属流向了轴向和径向；⑥当张力系数Z大于临界张力系数Zl时，Φl为正，Φr和Φt为负，说明钢管周向压缩和壁厚减薄的金属流向了轴向；⑦随着D/S值的增大，Φl、Φr、Φt随张力系数变化的斜率均有增大的趋势，说明张力系数对薄壁钢管的影响更大一些。

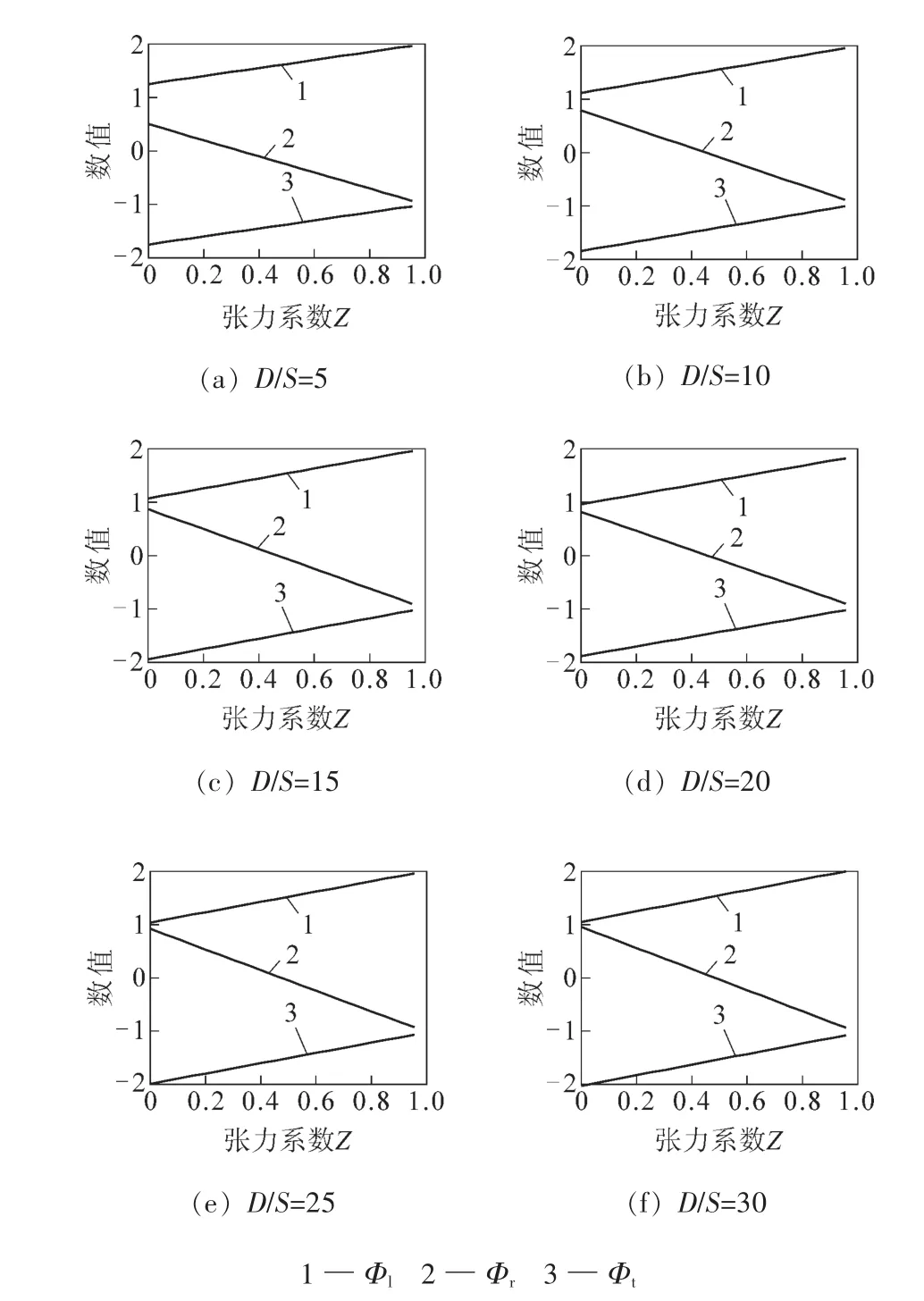
图2 Φl、Φr、Φt与张力系数Z的关系曲线

3 临界张力系数的特点

Φr=0时的张力系数即为临界张力系数Zl，计算不同D/S值情况下的临界张力系数，并绘制临界张力系数与D/S的关系曲线，如图3所示。

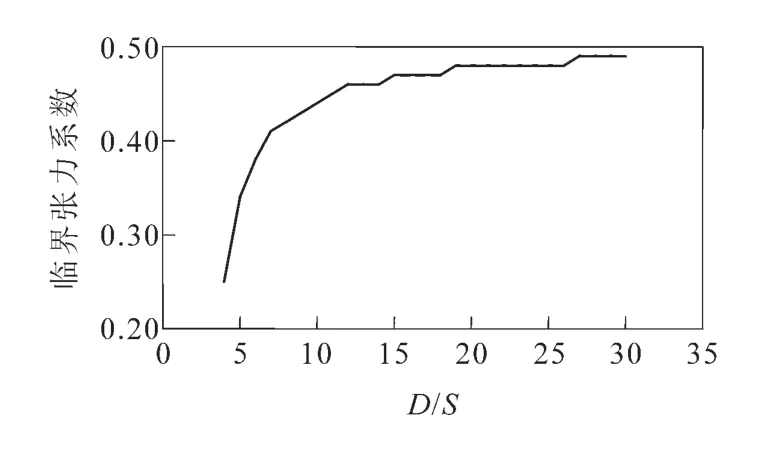
图3 临界张力系数与D/S的关系曲线

由图3可以看出：①随着钢管D/S值的增大，临界张力系数Zl也随之增大，说明对于壁厚越小的钢管越需要较大的张力系数才可发生减壁变形；②计算的临界张力系数的数值范围为0.35～0.50；当D/S=5时，Zl约为0.35；随着D/S的增大，Zl逐渐趋于0.50，而且当D/S超过15时，Zl的变化非常缓慢；③临界张力系数的上限值为0.50，说明在任何情况下，如果张力减径的张力系数超过0.50，则钢管会发生减壁变形。

4 实例应用

某无缝钢管厂有18机架张力减径机，减径前荒管规格为Ф95 mm×3.5 mm，预轧制成品管规格为Ф57mm×3.5mm。根据现场条件，选择18机架轧制，其孔型尺寸见表1。

表1 某18机架张力减径机孔型尺寸

本轧制条件为典型的等壁轧制，所以可根据D/S选择临界张力系数作为工艺计算模型的输入条件。张力减径入口荒管的D/S值为27.14，出口成品管的D/S值为16.28，根据图3所示曲线，其临界张力系数分别为0.47和0.48。考虑头部机架和尾部机架的张力损失，选择该轧制条件下临界张力系数上限值0.48作为输入参数进行工艺计算。表2为计算壁厚值与实测壁厚值的比较。

表2 计算壁厚值与实测壁厚值的比较

由表2可知：所计算的各机架钢管的壁厚值相对于实测壁厚的最大绝对偏差为-0.13 mm，最大相对偏差为-3.72%；成品钢管的计算壁厚与实测壁厚的绝对偏差为0.01 mm，相对偏差为0.29%。可以看出：计算壁厚与实测壁厚的数值比较吻合，可以满足实际生产的工艺控制要求。

5 结 论

（1）推导出钢管张力减径塑性方程式，提出以张力系数Z和径壁比D/S为自变量的表征钢管纵向、切向和径向变形的指标 Φl、Φr、Φt。

（2）增大张力系数有利于促进钢管的纵向延伸变形和减壁变形，不利于钢管的减径变形；在三向变形中，张力系数对壁厚变化的影响最为明显。

（3）钢管张力减径时，其临界张力系数Zl只受钢管径壁比D/S的影响，D/S越大，Zl越大。

（4）理论推导的临界张力系数值为0.35～0.50，任何情况下临界张力系数都小于0.50。

（5）实例分析表明，在钢管张力减径工艺计算中，根据钢管的D/S选择张力系数是有效可行的。

［1］易兴斌.热轧无缝钢管轧机选型的探讨［J］.钢铁技术，2007（6）：14-22.

［2］金如崧.张力减径技术的早期和近期发展（A1）——《无缝钢管百年史话》（续释 8-1）［J］.钢管，2003，32（4）：54-59.

［3］焦艳，段炜，彭龙洲.钢管张力减径工艺特点及设备选型［J］.金属世界，2012（3）：33-35，64.

［4］方志承，罗佩文.张力减径机的动力学和运动学的分析［J］.中国机械，2014（2）：189.

［5］吕建钢，李永刚，汤德瑞.国产Ф180 mm连轧管机组的装备水平及应用［J］.钢管，2014，43（3）：59-63.

［6］张芳萍，孙斌煜，杜晓钟，等.张力减径机轧辊孔型设计方法的研究［J］.现代制造工程，2006（10）：110-113.

［7］于辉，臧新良，杜凤山，等.无缝钢管张力减径过程内六方产生的模拟分析［J］.钢铁，2008，43（3）：53-56，60.

［8］李熹平，林军.厚壁钢管张力减径过程的变形规律研究［J］.锻压装备与制造技术，2012，47（3）：87-89.

［9］谷智慧，孔德南，杨全磊，等.钢管微张力减径增壁量的试验与探讨［J］.钢管，2005，34（1）：24-26.

［10］王国顺，孙英时.上限法在张力减径过程中的应用［J］.鞍山钢铁学院学报，2001，24（1）：16-20.

［11］远新军.金属塑性成形原理［M］.北京：冶金工业出版社，2012.

［12］彭大暑.金属塑性加工原理［M］.长沙：中南大学出版社，2014.

［13］（德）Reiner Kopp，Herbert Wiegels.金属塑性成形导论［M］.康永林，洪慧平，译.北京：高等教育出版社，2010.