顺序小波包图像压缩感知方法*

周四望,罗孟儒

(湖南大学 信息科学与工程学院,湖南 长沙 410082)

顺序小波包图像压缩感知方法*

周四望,罗孟儒†

(湖南大学 信息科学与工程学院,湖南 长沙 410082)

针对压缩感知中测量次数不确定的问题，提出了顺序小波包图像压缩感知方法.该方法选用小波包变换分解图像，降低信号稀疏度，将图像划分为大小相等的小波包系数块，利用小波包系数块数学期望与稀疏度之间的关系，对初始采样信号y0的长度进行预测；同时变长设置顺序压缩感知过程中采样信号y1,…,yn的长度，来减少解压缩端重构次数以及两端的通信次数，从而解决传统顺序压缩感知方法中存在的不足.实验表明该方法在重构次数和重构精度上优于传统顺序压缩感知方法.

小波变换；压缩感知；数学期望；图像

压缩感知理论(Compressed Sensing，CS)[1]已经在图像处理等领域[2-3]引起了极大的重视.CS中对于稀疏度为K的信号，可以通过M大小的采样值进行重构.文献[4]指出，当M=4K时信号能近乎完美重构，因此在大部分应用中，CS的采样长度选择上限4K.随着研究的深入，研究人员发现对于含噪声的K稀疏信号，只需M=O(Klog (N/K))就能够在多项式时间内鲁棒地恢复原信号[5].在基于模型的压缩感知方法中[6]，Baraniuk等人证明，若能增加小波树结构的先验信息，则CoSaMP算法仅需满足M=Ο(K)即可实现鲁棒重构.由于不同图像的结构等先验信息不尽相同，研究人员只能尽力寻找压缩感知重构所需M的界，不可能从数学上推导出M的值.因此在实际应用中，有时M取值过大，则会增加设备的采样负担、耗费更多的网络延时和其它资源[7-8].因而在保证图像恢复质量的前提下，尽可能地减少采样值是图像压缩感知处理中值得考虑的一个问题.

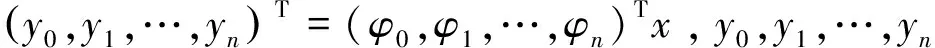
(1)

SequentialCS为尽可能减少采样值提出了解决方案，然而SequentialCS仍有以下2个方面值得考虑.其一，如何确定初始采样信号y0的长度.y0的长度直接影响着信号的传送以及重构次数.若y0的长度设置合理，重构和通信次数就会越少.然而SequentialCS相关方法对于如何确定y0的长度没有提出相应的解决方法.其二，如何确定y1,…,yn的长度.在实际应用中，如果重构信号间的误差很大，采样信号的长度相对取大些，这样能加快SequentialCS处理进程，从而减少通信次数及计算量；若误差相差不大，采样信号的长度取小些，就不会造成采样浪费.然而SequentialCS中，y1,…,yn的长度设定都是相同的，不能根据实际情况进行变长处理来减少计算量.

1 顺序小波包图像压缩感知方法

本文设计的顺序小波包图像压缩感知方法将解决以上两个问题.本文采用小波包变换对图像进行分解，进一步提高图像稀疏度.另外由于小波包变换将图像分为大小相等的小波包系数块，因而我们以小波包系数块为单位进行压缩感知测量，自然地降低了测量矩阵的维数.

1.1 基于数学期望的初始采样信号y0长度设置方法

本小节研究基于数学期望来预测初始采样信号y0长度的方法.由式(1)可知，y0为SequentialCS中压缩端首次传递给解压缩端的采样信号.y0长度的设置，对压缩端采样、解压缩端信号重构次数和信号传递次数都有着非常直接的影响.

我们知道小波包系数块的稀疏度是通过大系数的多少来反映的.在系数都为正数的情况下，数学期望值小的小波包块相对有更高的稀疏度.另外由于信号越稀疏，恢复信号所需的采样值就越少.因而在本文中我们根据小波包系数块之间数学期望与稀疏度的比例关系来对y0的长度进行预测，算法如图1所示.

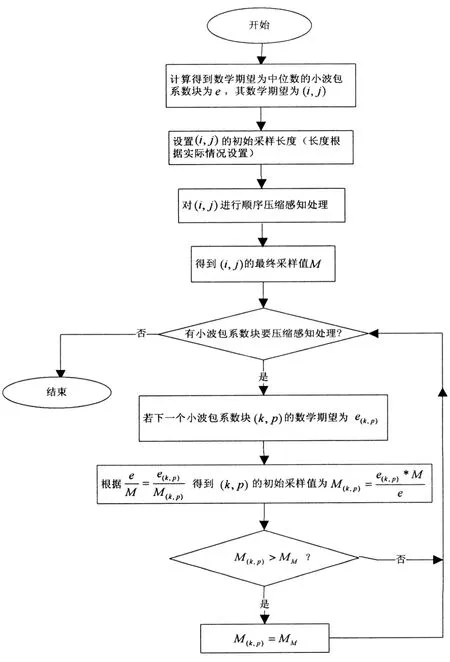
图1 基于数学期望的初始采样信号长度设置算法

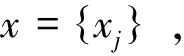
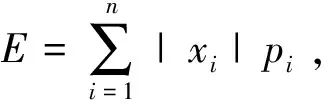
(2)

在图1中，数学期望为中位数的小波包系数块(i,j)是在计算需进行压缩感知处理的小波包系数块的数学期望后，对那些不为0的数学期望进行粗略排序得到；小波包系数块(k,p)指第k行第p个小波包系数块，它泛指除(i,j)外其他要进行压缩感知处理的小波包系数块.MM为最大采样长度，即y0长度最大不能超过MM.另外由于小波包系数块(1,1)为低频信号，它包含图像大部分信息，一般采用线性传输，因而不参与此过程.

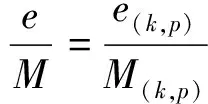
图2更清楚地阐述了本算法的实质.从图2可以看出，只要确定一个小波包系数块(i,j)的最终采样长度，那其他小波包系数块的初始采样长度就能根据(i,j)的数学期望和采样长度进行确定.在对(i,j)进行顺序压缩感知处理时，由于信息不充分，(i,j)的初始采样长度只能手动设置，故压缩端和解压缩端之间计算时间和通信次数没有太多的改变.但得到(i,j)最终采样长度后，就可以根据其数学期望和采样长度去预测其他小波包系数块初始采样长度.这样在对其他小波包系数块进行顺序压缩感知处理时，由于初始采样值设定合理，既能尽量少采样，又可以从整体上大大节省压缩端和解压缩端的计算压力以及通信次数.

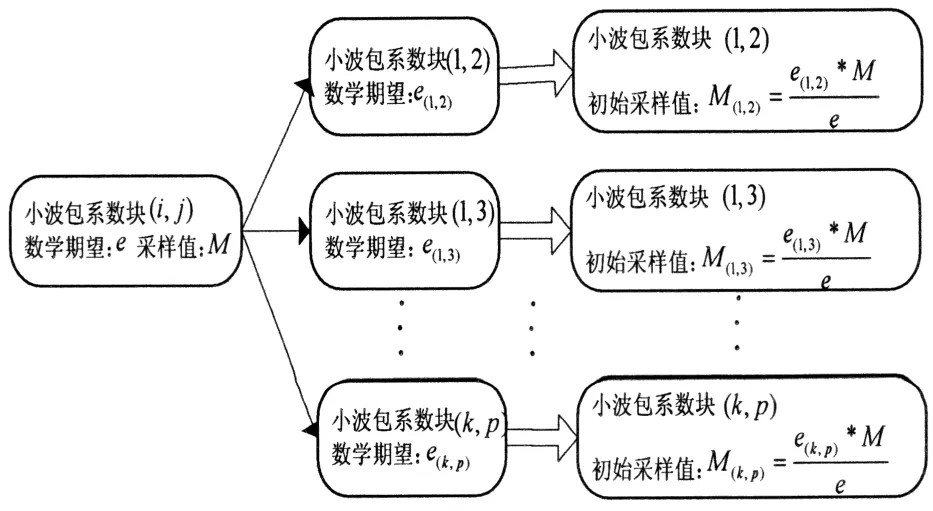
图2 基于数学期望的初始采样信号长度确定

1.2 变长设置的y1,…,yn长度

本节将变长设置y1,…,yn的长度.图3采用时序图的思路展示了对某一小波包系数块进行顺序压缩感知处理时，y1,…,yn的长度确定过程.其中Emin为常数.首先压缩端发送采样值yj-1给解压缩端，解压缩端收到信号后对其进行重构，计算两重构信号间的误差Ej-1，然后比较Ej-1与Emin，若Ej-1≤Emin说明重构图像满足误差要求，解压缩端让压缩端停止传送采样值，重构结束.若Ej-1>Emin则说明不能重构原信号，解压缩端让压缩端再次传送采样值yj，yj的长度nj=αEj-1*M，其中α为常系数，M为原始信号长度.这样依次传递直到满足要求为止.

从图3看出yj的长度nj是基于上一次误差进行确定的，从而根据图像重构效果变长设置y1,…,yn长度.此方法是借鉴TCP流量控制的思想，其中窗口的大小(即y1,…,yn的长度)由解压缩端进行控制，如yj的长度nj=αEj-1*M，解压缩端就是通过重构信号之间的误差Ej-1来控制下一次采样信号yj的长度，如图4所示，α控制窗口的规模，我们可以根据图像恢复的精度需要对α进行设置，Ej-1确定窗口的大小.只要把α设置为正数，那么两信号之间的误差Ej-1越大，nj也会相应地更长.这样就可以根据每个小波包系数块各自的特点，对y1,…,yn的长度进行自适应地调整.

图3 确定y1,…,yn长度

图4 yj窗口大小nj设置

2 实验结果及分析

本节进行模拟实验.实验平台为matlab7.0，电脑主频为2.53GHz，内存大小为2G.测试图像为Lena,Cameraman和BABOON，其中Lena包含丰富的细节和纹理特征，Cameraman前景和背景对比较大，BABOON平滑区域和细节区域较为明显.实验中，我们用“Symmlet”小波对图像进行4层小波包分解，观测矩阵为高斯矩阵，重构算法为OMP.

2.1 初始采样信号y0长度设置合理性验证

我们选取图像中6个位置(数学期望相对很靠前)的小波包系数块进行验证.我们依次增加信号采样比，观察信号误差随采样比的变化情况.

图5～图7分别是Lena，Cameraman，BABOON的小波包系数块采样比与误差的关系.图中横坐标为采样值占信号总长度百分比，纵坐标为原小波包系数块与重构后小波包系数块的误差.如图5所示(3,1)1.078表示小波包变换后，位于图像第3行第1块的小波包系数块的数学期望为1.078.

采样比

采样比

采样比

2.2 变长设置y1,…,yn长度合理性验证

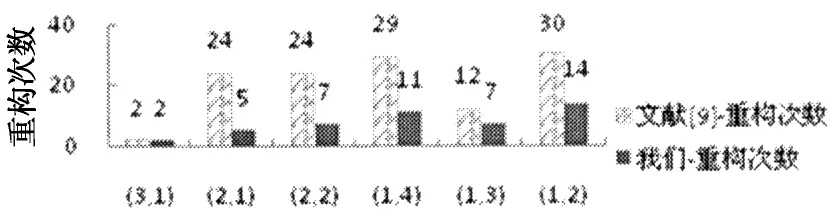
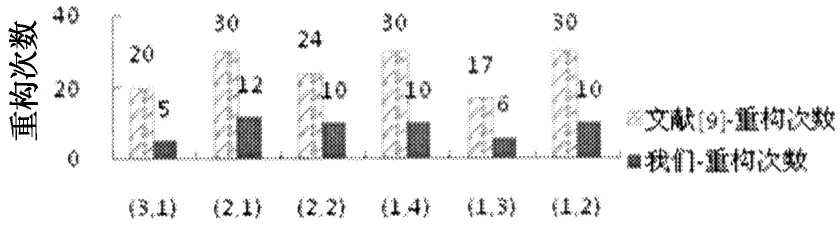
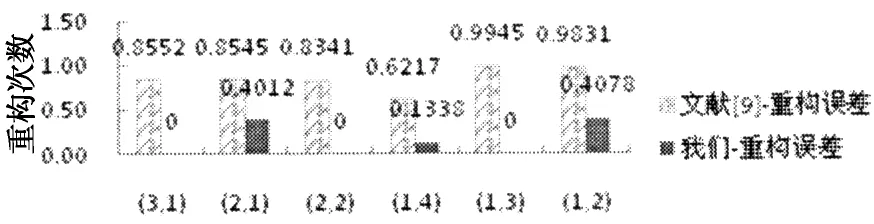
本实验中，对比实验为文献[9]中(即传统顺序压缩感知方法)等长设置y1,…,yn.设y0的采样比为0.1，信号总采样比不高于0.7.等长方法设置y1,…,yn长度时，y1,…,yn的采样比为0.02.变长设置时，我们根据Sj与Sj-1的误差E(Sj,Sj-1)大小进行设置，令α=0.1，则采样比为E(Sj,Sj-1)×0.1，精确到小数点后两位.若E(Sj,Sj-1)=0.827，则yj+1的采样比为0.08.图中，“文献[9]-重构”表示文献[9]中的等长设置方法，“我们-重构”表示我们提出的变长设置方法.

图8～图10是Lena,Cameraman和BABOON等长和变长设置y1,…,yn采样值的重构次数比较结果.横坐标表示所处位置的小波包系数块，如图8中(3,1)指位于图像第3行第1块的小波包系数块.纵坐标为SequentialCS处理时解压缩端的信号重构次数.从图8～图10中可以看出变长设置y1,…,yn解压缩端所需的重构次数比等长设置少.

小波包系数块

小波包系数块

小波包系数块

图11～图13是Lena,Cameraman和BABOON等长和变长设置y1,…,yn重构次数相同时各小波包系数块的误差比较结果.图中横坐标表示所处位置的小波包系数块，纵坐标为重构信号与原始信号之间的重构误差.实验中，重构次数是每个小波包系数块变长设置y1,…,yn重构误差为0或者采样总长度到达最大采样值MM时的重构次数.从图11～图13中看出，在重构次数相同的情况下，变长设置y1,…,yn的重构误差相比等长设置的重构误差要小.

图14展示了大小为512×512的Lena,Cameraman和BABOON采用等长和变长设置y1,…,yn重构次数相同时重构图像对比.其中，低频信号进行线性传递，小波包系数块(3,1),(2,1),(2,2),(1,4),(1,3),(1,2)分别采取等长和变长设置y1,…,yn方法得到，其他小波包系数块不进行信号采样.从图14可以更直观地看出，在重构次数相同的情况下，变长设置y1,…,yn的重构误差比等长设置的小.

小波包系数块

小波包系数块

小波包系数块

图14 重构图像对比

通过上述实验，可以看出在完全重构信号时，变长设置y1,…,yn采样长度解压缩端所需重构次数更少.当重构次数相同时，变长设置y1,…,yn比等长设置重构得到的误差小.

3 结 论

在CS中，减少采样长度意味着减少设备的采样负担、计算时间以及网络传输压力.SequentialCS为尽可能减少采样值提出了新思路，但仍存在一些不足.本文提出的顺序小波包图像压缩感知方法通过对图像进行小波包分解，从而对y0的长度进行预测，同时借鉴TCP流控制的思想变长设置y1,…,yn的长度，从整体上降低压缩端和解压缩端的通信次数和运算负担.实验表明，根据小波包系数块的期望值对y0进行预测、变长设置y1,…,yn的长度是合理的.

[1]BARANIUKRG.Compressivesensing[J].IEEESignalProcessingMagazine, 2007, 24(4):118-121．

[2] 张汗灵,李红英,周敏.融合多特征和压缩感知的手势识别[J].湖南大学学报:自然科学版,2013,40(3):87-92．

ZHANGHan-ling,LIHong-ying,ZHOUMin.Handposturerecognitionbasedonmulti-featureandcompressivesensing[J].JournalofHunanUniversity:NaturalSciences, 2013, 40(3): 87-92.(InChinese)

[3]ROSTAMIM,MICHAILOVICHO,ZHOUW.Imagedeblurringusingderivativecompressedsensingforopticalimageapplication[J].IEEETransactionsonImageProcessing, 2012, 21(7):3139-3149．

[4]DONOHODL,TSAIGY.Extensionsofcompressedsensing[J].SignalProcessing, 2006, 86(3):533-548．

[5]DUARTEMF,CEVHERV,BARANIUKRG.Model-basedcompressivesensingforsignalensembles[C]//2009 47thAnnualAllertonConferenceonCommunication,ControlandComputing(Allerton2009).Monticello:InstituteofElectricalandElectronicsEngineers(IEEE),2009: 244-250．

[6]BARANIUKRG,CEVHERV,DUARTEMF,etal. Model-based compressive sensing [J]. IEEE Transactions on Information Theory, 2010, 56(4):1982-2001．

[7] YANG J G, THOMPSON J, HUANG X T,etal. Random-frequency SAR imaging based on compressed sensing [J]. IEEE Transactions on Geosciences and Remote Sensing, 2013, 51(2):983-994．

[8] XIANG S Y, CAI L. Transmission control for compressive sensing video over wireless channel [J]. IEEE Transactions on Wireless Communications, 2013, 12(3):1429-1437．

[9] MALIOUTOV D M, SANGHAVI S R, WILLSKY A S. Sequential compressed sensing [J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):435-444.

[10]ASIF M S, ROMBERG J. Streaming measurements in compressive sensing: L1 filtering [C]//2008 42nd Asilomar Conference on Signals, Systems and Computers. Pacific Grove: Institute of Electrical and Electronics Engineers (IEEE), 2008: 1051-1058.

[11]HAO J P, TOSATO F, PIECHOCKI R J. Sequential compressive sensing in wireless sensor networks[C]// 2012 IEEE 75th Vehicular Technology Conference (VTC Spring 2012). Yokohama, Japan: Institute of Electrical and Electronics Engineers (IEEE), 2012: 1-5.

Sequential Image Compressed Sensing Based on Wavelet Packet

ZHOU Si-wang,LUO Meng-ru†

(College of Information Science and Engineering, Hunan Univ, Changsha,Hunan 410082,China)

Aiming at solving the problem of the times of measurements, a scheme of sequential compressed sensing based on wavelet packet was proposed. The wavelet packet transform was firstly employed and the image was decomposed into wavelet packet blocks with the same size. The length of the initial sampling signal was then estimated using the relationship between the mathematical expectation and the sparsity of wavelet packet blocks. Meanwhile, the lengths of sampling signals were set dynamically in order to reduce the reconstruction and communication overhead. The problem of uncertain times of measurements in the traditional compressed sensing was thus overcome. Experimental results show that our proposed scheme has less reconstruction times and lower reconstruction error than the existed ones.

wavelet transforms; compressed sensing; mathematical expectation; image

1674-2974(2015)04-0130-06

2014-02-27

国家自然科学基金资助项目(60973127)，National Natural Science Foundation of China(60973127) ；教育部新世纪优秀人才计划基金资助课题(NCET-11-0136)，湖南省自然科学基金资助项目(14JJ2051)

周四望(1971-)，男，湖南岳阳人，湖南大学副教授，博士

†通讯联系人，E-mail:loumengru1988@126.com

TN911.73

A