表面粗糙度对双曲冷却塔风压分布的影响*

邹云峰，何旭辉，王汉封，谭立新，牛华伟

(1．中南大学 土木工程学院，湖南 长沙 410075；2．高速铁路建造技术国家工程实验室，湖南 长沙 410075；3．中国建筑第五工程局有限公司，湖南 长沙 410004；4．湖南大学 风工程试验研究中心，湖南 长沙 410082)

表面粗糙度对双曲冷却塔风压分布的影响*

邹云峰1,2,3，何旭辉1,2†，王汉封1,2，谭立新3，牛华伟4

(1．中南大学 土木工程学院，湖南 长沙 410075；2．高速铁路建造技术国家工程实验室，湖南 长沙 410075；3．中国建筑第五工程局有限公司，湖南 长沙 410004；4．湖南大学 风工程试验研究中心，湖南 长沙 410082)

对不同粗糙条参数组合下冷却塔风压分布进行测试，分析粗糙度对平均风压和脉动风压的影响.研究结果表明：粗糙条宽度b对风压分布影响较小，而粗糙条高度k和数量n影响较大；粗糙度系数k/s能较准确描述粗糙度大小，当k/s一致时，不同粗糙条数量n与高度k组合下的平均风压基本一致，但高度大的脉动风压小；粗糙度对正压分布和背压大小影响较小，而最小负压系数幅值、脉动风压系数峰值随粗糙度的增大而减小，背压稳定区宽度则略有扩大；尽管通过增大模型表面粗糙度能有效地在较低雷诺数条件下实现高雷诺数下的平均风压分布，但脉动风压模拟的准确性需要通过大型冷却塔风压实测进行验证.

冷却塔；表面粗糙度；风压分布；风洞试验

冷却塔属类圆截面结构，风压分布受表面粗糙度和雷诺数影响显著.风洞试验由于采用缩尺模型导致试验雷诺数比实际的小2～3个数量级，又由于风洞试验中风速的限制，很难通过增加试验风速来提高雷诺数，因此一般通过增大模型表面粗糙度对类圆截面结构的雷诺数效应进行补偿[1-2].此外，随着冷却塔高度的增加，国外通常在风筒外表面设置子午向肋条来增大表面粗糙度以减小最小风压系数幅值[3-4].

目前，已有一些文献研究了表面粗糙度对冷却塔风荷载的影响.Armitt发现在一定粗糙度范围内，可以通过增加模型表面粗糙度模拟较高雷诺数下的光塔平均风压[5]；Farell等研究表明最小负压系数随粗糙度的增大而减小[6]；Niemann分析了粗糙度对最小负压、背压等冷却塔风压曲线特征值的影响，并给出不同粗糙度下的拟合曲线[7]；孙天风等发现最小压力系数幅值随着表面粗糙度的增大而减小，粗糙度大小与粗糙条厚度和数量有关[8]；刘天成等对刻线和粘贴丝线、粗糙纸带等多种增大表面粗糙度手段对雷诺数效应补偿效果对比，发现粘贴粗糙纸带较为有效且便于操作[9]；沈国辉等通过两种粗糙条数量和五种粗糙条厚度对比分析发现结构的整体受力随粗糙条数量和厚度的增加而增大[10]；董国朝等的数值模拟结果表明冷却塔表面混凝土粗糙度对风压分布的影响不容忽视[11].以上研究主要定性分析粗糙度对冷却塔平均风荷载的影响，几乎没有涉及脉动风荷载；没有总结出合理的粗糙度系数，未能定量分析粗糙度对风压分布的影响大小.如何调整粗糙度以保证在风洞试验中模型表面绕流特性与原型一致或接近以确保风洞试验结果可靠，怎样考虑子午向肋条(宽度、高度、间距等)对风压分布的影响以确保原型冷却塔表面的风压分布与设计曲线(加肋曲线)相符，等等.这些问题的解决需要对表面粗糙度影响风压分布(平均风压和脉动风压)的规律进行系统地深入分析.

本文进行粗糙条参数如数量、厚度、宽度等多种组合工况的冷却塔刚性模型测压试验，对脉动风压进行反演修正以确保其测试结果的可靠性，较系统的分析粗糙条参数对冷却塔风压分布的影响，定义更为合理的粗糙度系数，总结粗糙度系数与风压分布曲线之间的关系，并与实塔测试结果验证.研究成果为全面认识表面粗糙度对冷却塔风压分布的影响提供参考.

1 风洞试验概况

1.1 试验模型

某核电站拟建冷却塔塔顶标高200.20 m，喉部标高156.70 m，进风口标高12.59 m，塔顶直径96.60 m，喉部直径94.60 m，底部直径153.00 m，风筒采用分段等厚，最小厚度在喉部断面为0.25 m，最大厚度在下环梁位置为1.4 m，由均匀分布的52对人字柱支撑.试验模型几何缩尺比为1/400，采用圆柱型铝锭通过数控机床精加工而成，精度可达±0.01 mm，严格保证外形与实际结构保持几何相似，模型底部由缩尺的人字柱支撑.模型壁厚6 mm，保证模型具有足够的强度和刚度，在试验风速下不发生变形及不出现明显的振动.在模型表面共布置20层测点，每层沿环向等间距布置36个测点，共计720个测点，测点布置如图1所示.试验在湖南大学HD-2风洞的高速试验段进行，试验段长17 m，宽3 m，高2.5 m.为使试验结果更具普遍性，本次试验在均匀流场中进行.

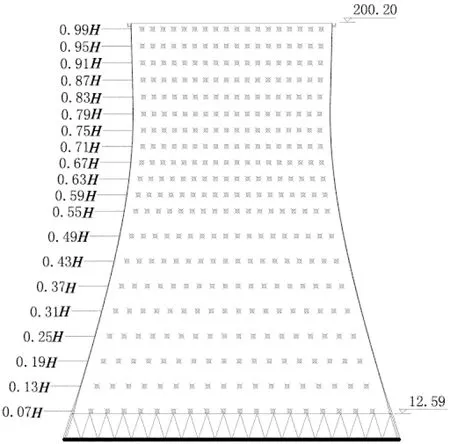
图1 测压点布置

1.2 试验工况

参考常用方法，通过在模型表面沿环向等间距粘贴子午向通长的粗糙纸带增大表面粗糙度，粗糙度大小改变通过调整纸带宽度、厚度、数量实现，其中，纸带宽度考虑5,8,10,15 mm 4种，厚度在0.0(光塔)～0.8 mm范围内以0.1 mm为增量逐一变化，数量考虑36,72条2种，试验风速在6～20 m/s内以2 m/s为增量逐一变化，对应的雷诺数范围为0.99×105～3.3×105，总共约进行了200个吹风工况.详细的工况安排见表1，部分试验照片如图2所示.

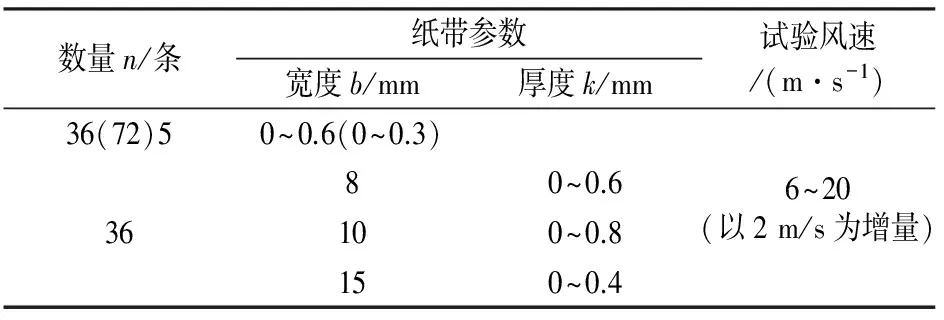
表1 试验工况

图2 粗糙度模拟试验照片

2 参数定义

2.1 压力系数

在空气动力学中物体表面的压力通常采用无量纲压力系数来表示，冷却塔表面任意测点i处的风压系数CPi表示为：

(1)

式中Pi为测点i处的压力，以指向结构表面为正，离开为负；P∞为参考高度处的来流静压；ρ为空气密度，取ρ=1.225kg/m3；Vi为测点i高度处来流风速.

2.2 风压曲线特征值

要研究粗糙度对风压分布的影响，首先要找到能准确描述风压分布曲线特征的参数，研究它们和粗糙度大小之间的关系.由于圆截面结构的风压曲

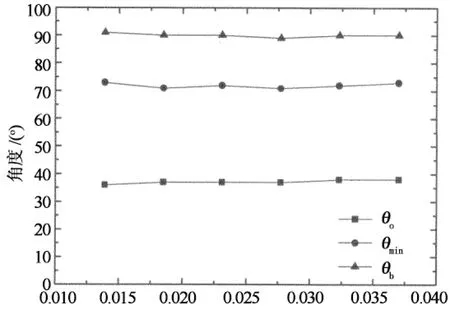
线关于来流对称分布，分布曲线可以由一些重要的特征点来描述(图3)：1)最大正压系数Cpmax，一般为1.0；2)风压为零的角度θ0；3)最小负压系数Cpmin及其发生的角度θmin；4)背压系数Cpb及其发生的角度θb，这个角度也是分离点的位置，事实上，背压系数Cpb一直沿圆周角变化，因此很难定义它发生的角度θb，本文定义θmin以后第一个风压曲线斜率为零的点所在圆周角为θb，背压系数Cpb取θb～180°各点的平均值.

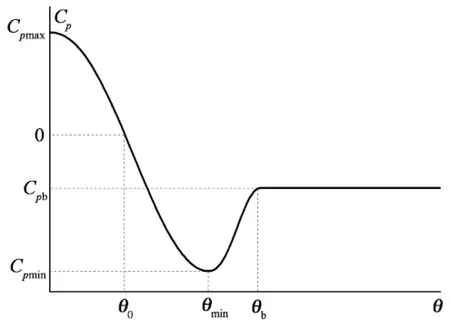
图3 风压曲线特征值

2.3 粗糙度系数

图4所示为在结构物表面布置粗糙条参数示意图，其中k为粗糙条高度，b为宽度，s为两粗糙条中心间距，D为结构的直径.已有研究大多以k/D衡量粗糙度大小，例如，Buresti(1981)[12]，Shih W C L(1993)[13]，操金鑫(2009)[14]等.事实上这一系数忽略了粗糙条数量的影响，可以想象，当粗糙条数量足够多以致两两相接时，“粗糙塔”变成了“光塔”，只是直径增大了2k.设结构表面布置的粗糙条数量为n，由于粗糙条通常沿圆周等间距布置，本文定义粗糙度系数如下：

(2)

由式(2)可以看出，k/s不仅包含了k/D，还可以考虑粗糙条数量n的影响，定义更为合理，本文重点分析风压分布特征值与该系数之间的关系.

图4 粗糙条参数示意图

3 畸变脉动风压反演修正

测压试验中，模型表面的风压通常需要由一定长度的测压管道传输至压力传感器，在这一传输过程中，传感器测得的脉动压力信号实际上是模型表面真实风压发生畸变后的信号，反演修正是减小畸变的有效方法之一[15].反演修正的前提是准确获得测压管路系统的频率响应函数，本文在试验前采用比较法对所用测压管路系统的频率响应函数进行了测试[16].风压测量完成后，采用测得的频率响应函数对各测点的风压信号进行反演修正，以保证由脉动风压测试结果的正确和可靠性.图5给出的是测量得到的频率响应函数幅值及相位随频率的变化情况，图6所示为反演修正前后风压信号在时域和频域的对比，由图5和图6可以看出畸变风压修正的必要性和反演修正的有效性.

频率/Hz(a) 幅值

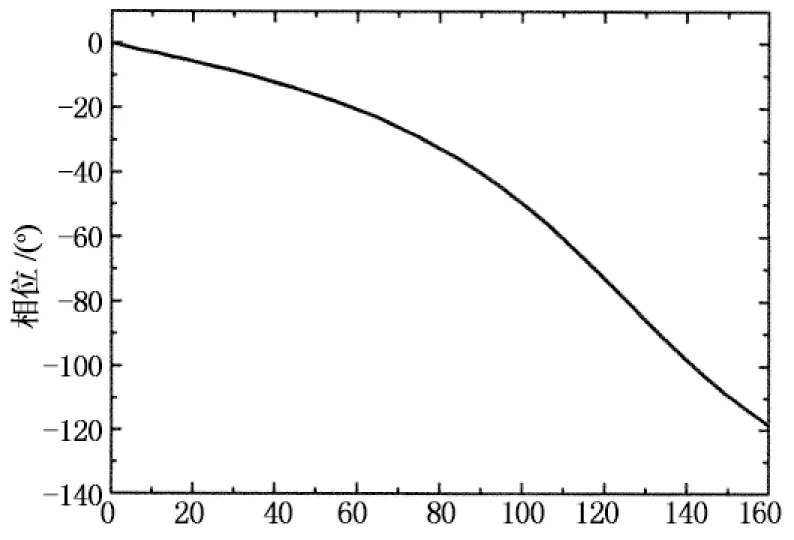
频率/Hz(b) 相位

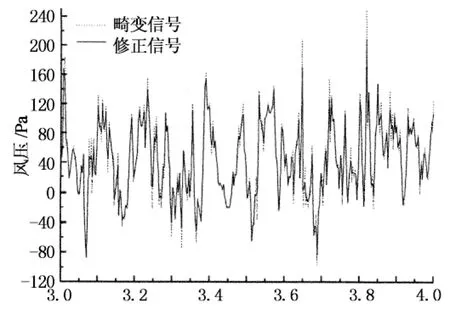
时间/s(a) 时域比较

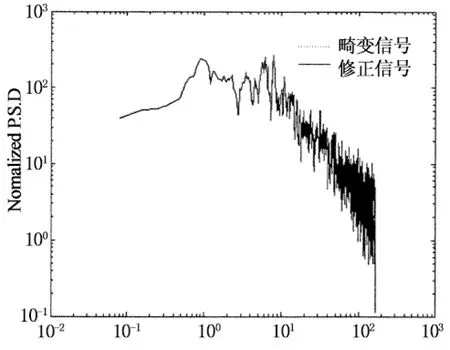
时间/s(b) 频域比较

4 粗糙条参数对风压分布的影响

考虑到冷却塔表面风压分布具有三维效应，即风压大小不仅与圆周角有关，还与测点所处高度有关，且由于不同高度处的圆截面半径不一样，粗糙条又沿子午向通长布置，故粗糙度系数k/s也随高度变化，因此本文选取0.55H～0.79H中段各测层的平均风压曲线作为“代表性曲线”，考察该高度范围内的平均粗糙度系数对“代表性曲线”特征值的影响.此外，考虑到测试结果的波动性及测点沿环向圆周角的间距较大，为准确比较粗糙度对最小风压系数、背压等特征值发生角度的影响，将“代表性曲线”的用最小二乘法进行拟合，拟合的函数公式为中国规范推荐的傅里叶八项式.

4.1 粗糙条宽度b对风压分布的影响

图7给出的是典型亚临界和临界雷诺数下在保证粗糙条高度k和间距s相同时比较粗糙条宽度b对风压分布影响的比较结果，从图中可以看出，不管是在亚临界还是临界雷诺数下，不同粗糙条宽度b下的风压分布基本一致，表明冷却塔表面风压分布受粗糙条宽度影响较小.

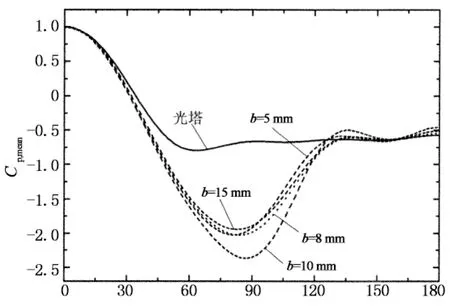
圆周角/(°)(a) 平均风压(Re=2.31×105)

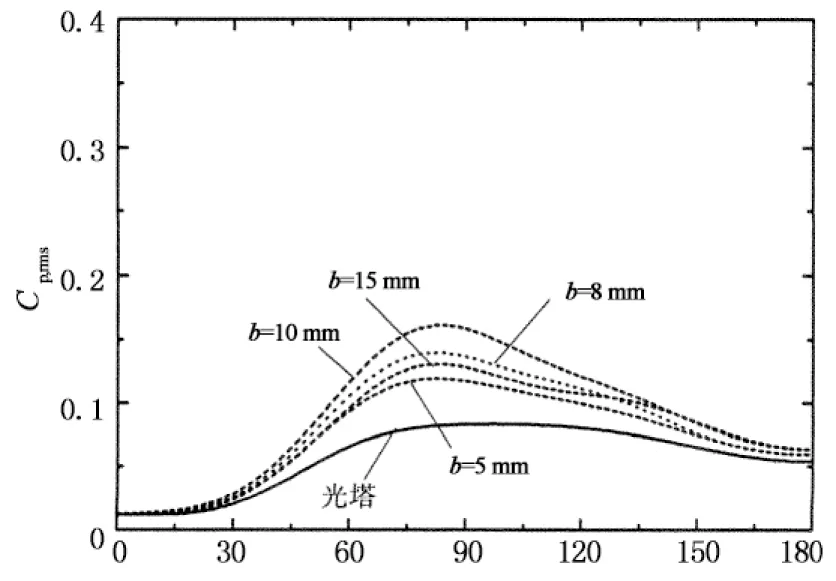
圆周角/(°)(b) 脉动风压(Re=2.31×105)

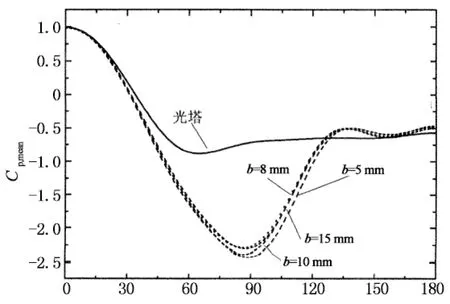
圆周角/(°)(c) 平均风压(Re=3.31×105)

圆周角/(°)(d) 脉动风压(Re=3.31×105)

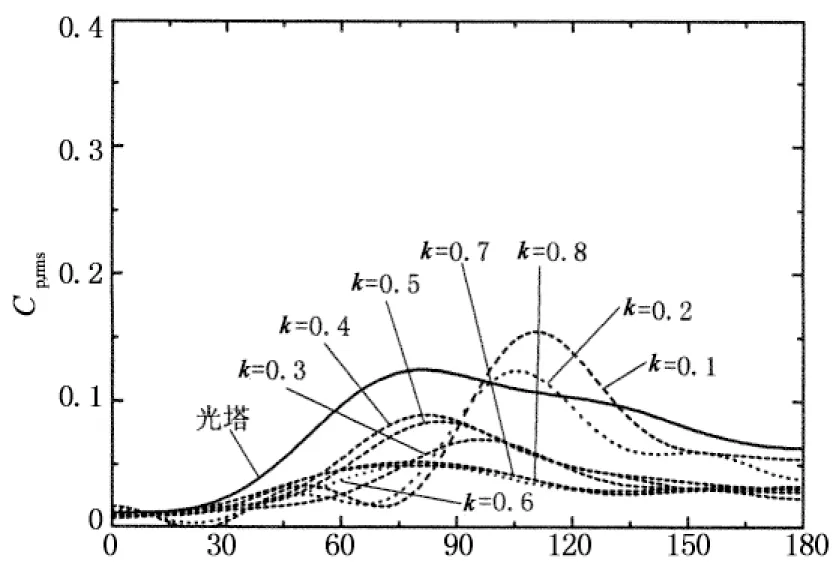
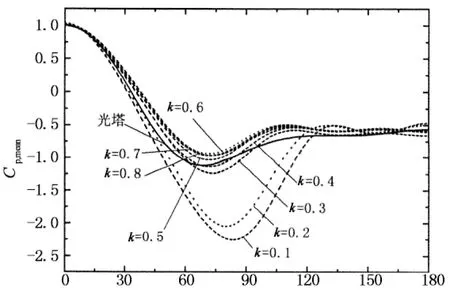
4.2 粗糙条高度k对风压分布的影响

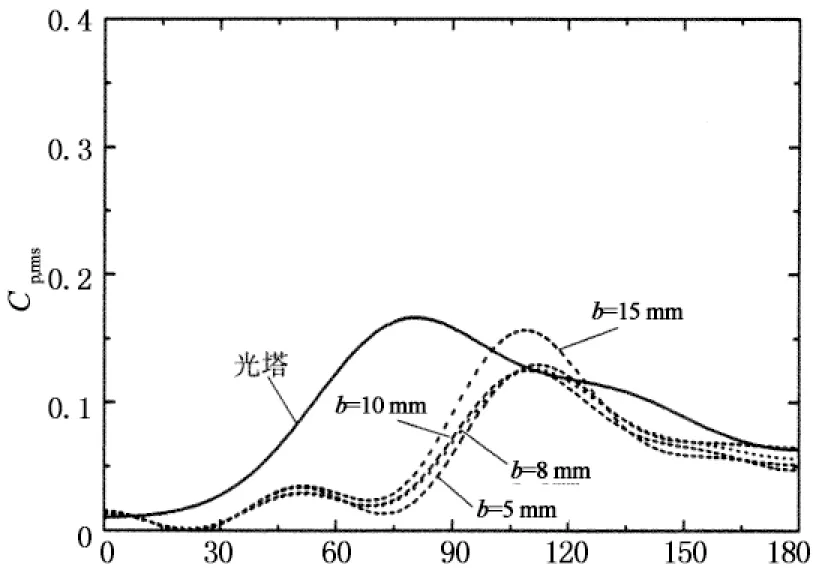
圆周角/(°)(a) 平均风压(Re=2.31×105)

圆周角/(°)(b) 脉动风压(Re=2.31×105)

圆周角/(°)(c) 平均风压(Re=3.31×105)

圆周角/(°)(d) 脉动风压(Re=3.31×105)

图8给出的是典型雷诺数下在保证粗糙条宽度b和间距s相同时比较粗糙条高度k对风压分布影响的比较结果.通过这些图的比较分析可以看出，对于平均风压而言，粗糙条高度对正压区风压分布和背压大小影响较小，而负压区风压分布和背压稳定区宽度受它影响较大；由于试验雷诺数较小，光塔的绕流特性属于亚临界状态(Re=2.31×105)或刚进入临界状态(Re=3.31×105)，表面粗糙度一旦增大后，例如k=0.1，绕流特性立即进入临界状态，最小负压系数幅值达到最大值，背压稳定区宽度减小，此后，随着粗糙条高度的进一步增加，绕流特性进入超临界或高超临界，最小负压系数幅值减小，背压稳定区宽度增大，当粗糙度增大至一定程度后，模型表面的绕流特性已经稳定，风压分布特征基本不再随粗糙条高度变化，故粗糙条高度的增大效果类似于雷诺数增加；对于脉动风压，峰值基本随粗糙条高度的增大而减小.Ribeiro[17]认为脉动风压主要来源于来流湍流和结构在横风向的漩涡脱落，且±90°圆周角附近的脉动风压主要由漩涡脱落贡献，由于来流湍流和脱落漩涡的相互作用，会导致涡旋强度及稳定性减弱，使得该区域的脉动风压减小.由于增大表面粗糙度的本质作用在于诱发边界层提前转捩，促使边界层由层流分离转变为湍流分离，结合Ribeiro的观点可知，粗糙条高度k越大，其产生的特征湍流强度越大，使得脉动风压峰值减小，因此在雷诺数效应模拟过程中粗糙条高度不宜过大.

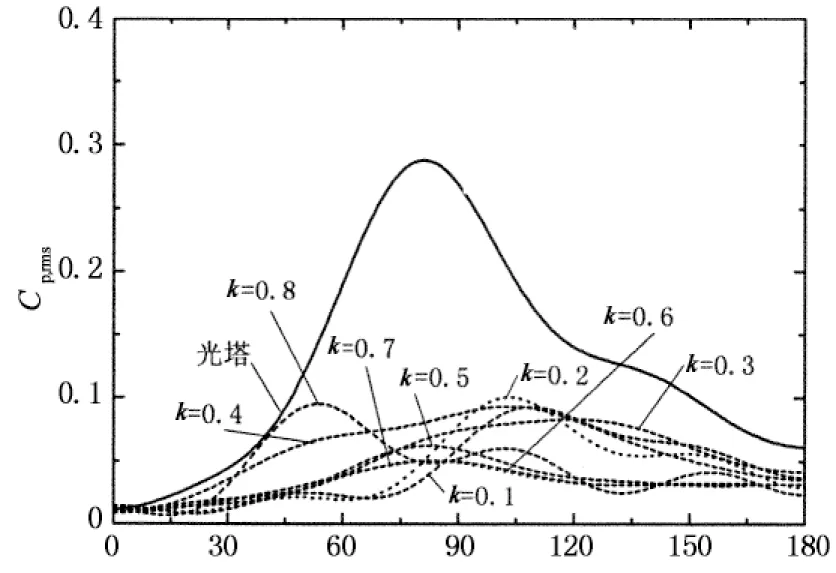
4.3 粗糙条间距s对风压分布的影响

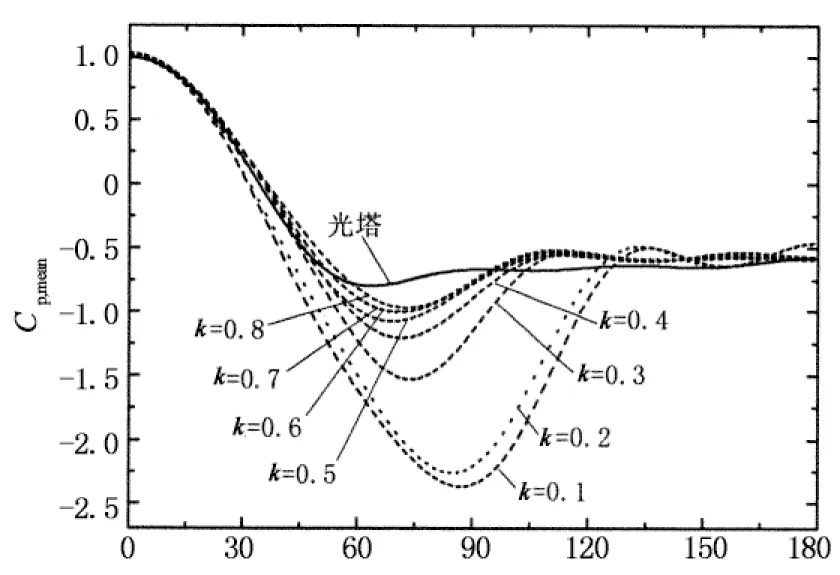
图9给出的是在亚临界和临界绕流状态下保证粗糙条高度k和宽度b一致时比较粗糙条间距s对风压分布影响的比较结果，其中间距s的变化通过改变粗糙条的数量n实现.通过这些图的对比分析可以发现，不同粗糙条数量下的平均、脉动风压分布差别较大，并以负压区的平均风压尤为显著；当n=36的风压分布呈亚临界绕流特性时，n=72的绕流特性则开始进入临界区域，最小平均风压系数和背压稳定区宽度均显著减小；当n=36的表面绕流特性呈临界状态时，n=72的最小负压系数幅值减小，背压稳定区宽度增大，绕流特性向高超临界过渡.综上所述，粗糙条数量n大时，表面粗糙度较大.

圆周角/(°)(a) 平均风压(Re=2.31×105)

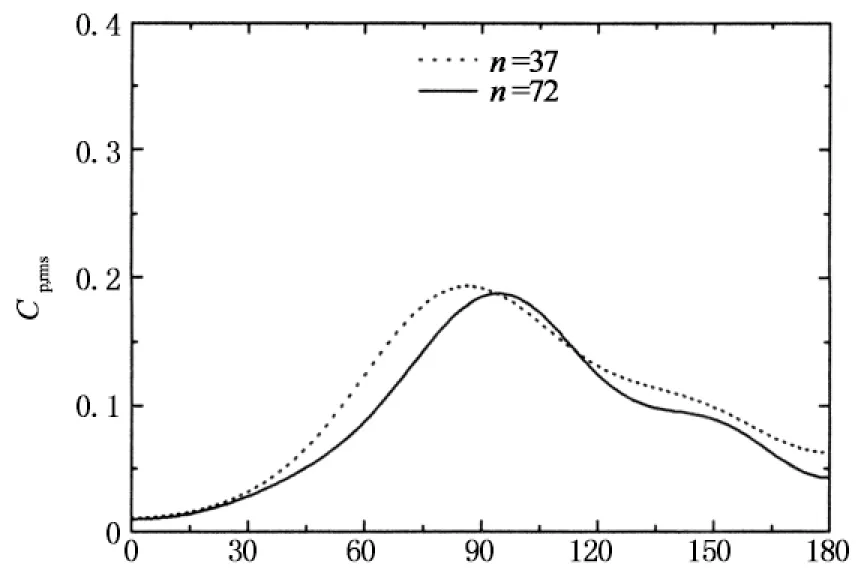
圆周角/(°)(b) 脉动风压(Re=2.31×105)

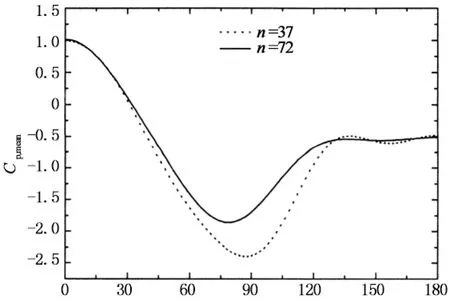
圆周角/(°)(c) 平均风压(Re=3.31×105)

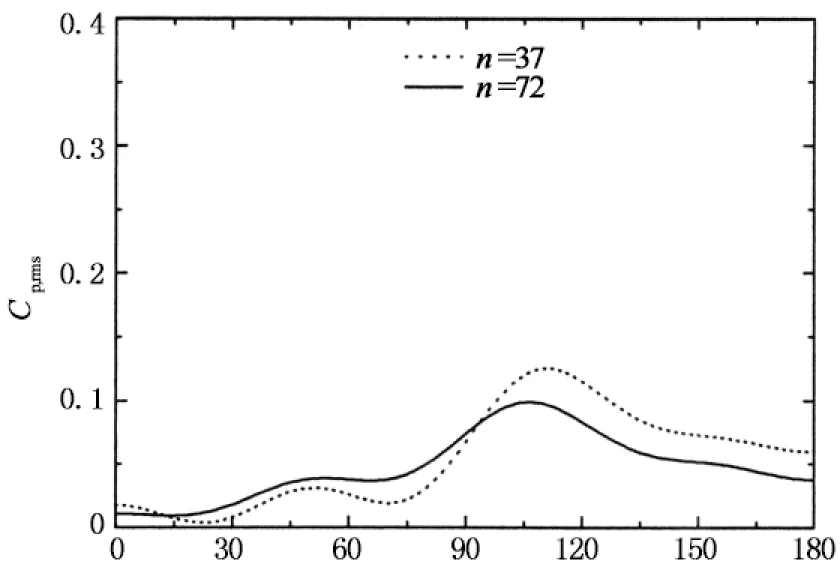
圆周角/(°)(d) 脉动风压(Re=3.31×105)

事实上，当结构表面粗糙条数量不是太大以致粗糙条没有两两相接时，可以直观的想象，当粗糙条高度k和宽度b一致时，肯定是粗糙条数量n较大时的粗糙度大，这进一步表明粗糙度系数k/D并不能完全描述粗糙度大小，粗糙度大小还与粗糙条数量n相关.

5 风压曲线特征值与粗糙度系数的关系

5.1 粗糙度系数的验证

为进一步验证粗糙度系数k/s能否较准确描述粗糙度大小，图10给出的是在典型亚临界和临界雷诺数下保证粗糙条宽度b和粗糙度系数k/s一致时，比较粗糙条数量n对风压分布影响的比较结果，通过这些图的对比分析可以看出，不管是在亚临界还是临界雷诺数下，当粗糙度系数k/s一致时，尽管两种工况的粗糙条数量n与厚度k不同，但它们的平均风压基本一致，n=72时的脉动风压峰值略大于n=36，其原因在于粗糙条数量大时厚度k较小，而脉动风压峰值与粗糙条高度k呈反比，这进一步表明通过增大模型表面粗糙度对雷诺数效应补偿进行补偿时，粗糙条高度不宜过大.由于图中比较的两种工况粗糙条数量n不同(即间距s不同)而k/s一致，因此粗糙条数量n大时，厚度k较小，反之，粗糙条数量较少时，厚度k较大，即两种工况的粗糙条高度k和间距s都不一样，由此可见，粗糙度大小不能单一以粗糙条高度k或间距s来描述，粗糙度系数k/s才是准确衡量粗糙度大小的重要参数.

圆周角/(°)(a) 平均风压(Re=2.31×105)

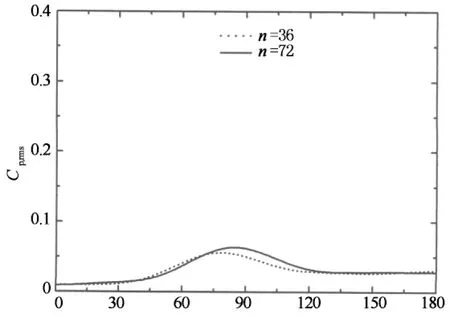
圆周角/(°)(b) 脉动风压(Re=2.31×105)

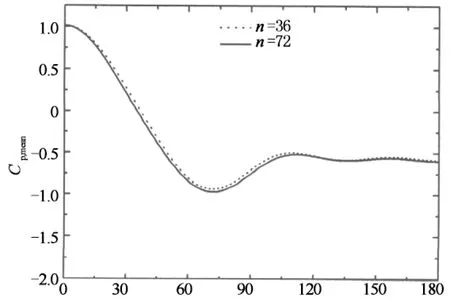
圆周角/(°)(c) 平均风压(Re=3.31×105)

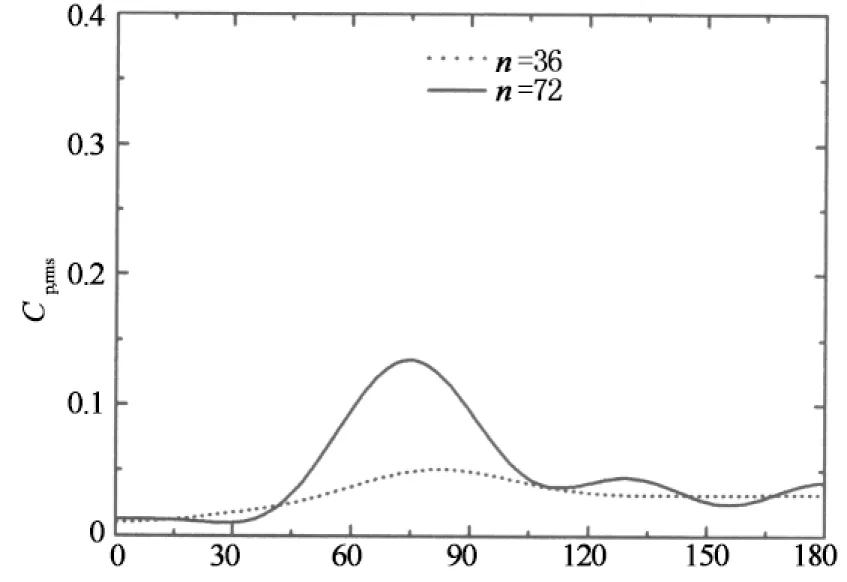
圆周角/(°)(d) 脉动风压(Re=3.31×105)

5.2 风压曲线特征值与k/s的关系

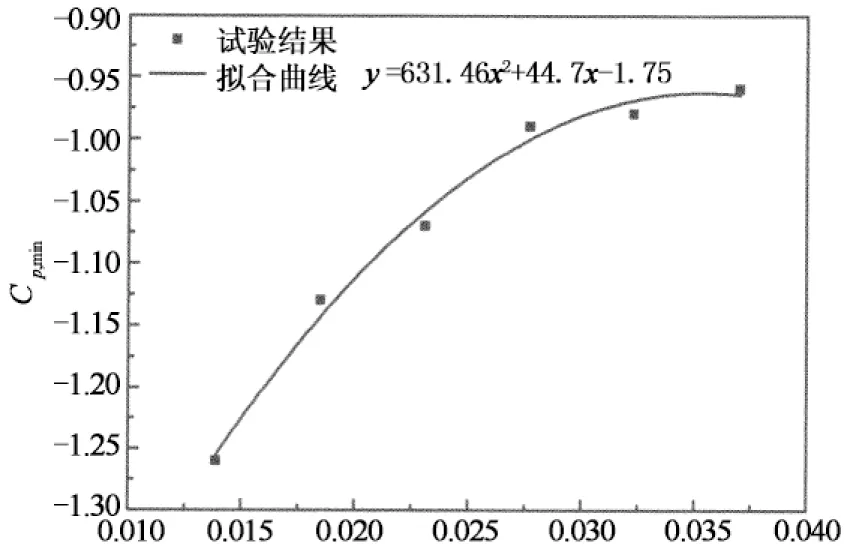
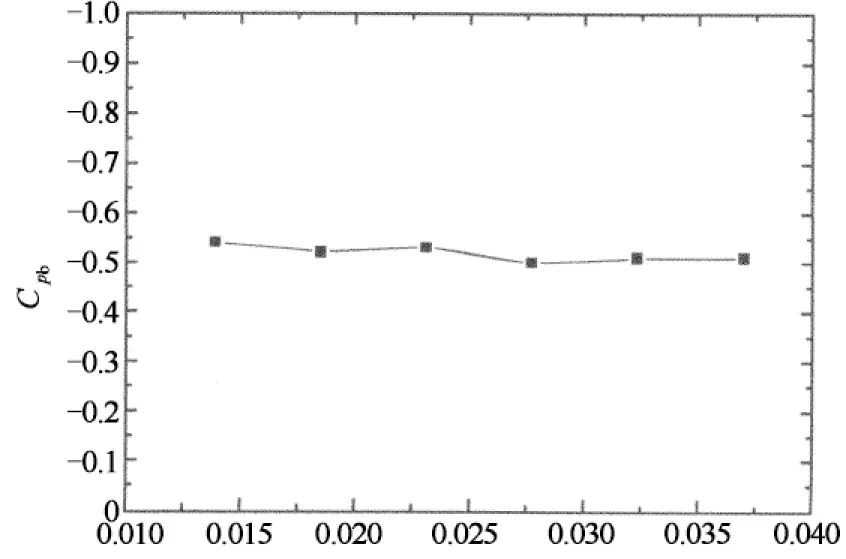
图11给出的是风压分布曲线特征值随粗糙度系数k/s的变化曲线，需要说明的是，由于本文的试验雷诺数较小，当粗糙度小于某一值时，风压分布还随雷诺数的增加而变化，表明模型表面的绕流特性尚未进入“自准区”，此时得到的特征值结果特别是最小负压系数Cpmin意义不大，因此仅给出绕流特性进入“自准区”即风压分布不再随雷诺数的增加而变化时的结果.从图11(a)可以看出，最小负压系数Cpmin的幅值随粗糙度系数k/s的增大而略微减小，且当k/s>0.028后，|Cpmin|基本不再变化，大小约为1.0，二者大致存在以下关系：

(3)

如图11(b)和(c)所示，当绕流特性进入“自准区”后，θb,θ0,θmin及Cpb等参数基本不随粗糙度变化(这与高超临界雷诺数下绕流特性稳定的特征相符)，分别约为90°,37°,72°和-0.52.

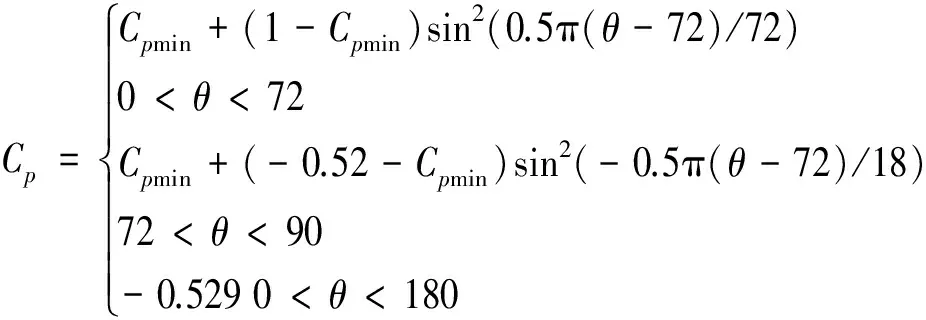
(4)

k/s(a) 最小负压系数Cpmin

k/s(b) 特征角度

k/s(c) 背压系数Cpb

5.3 验 证

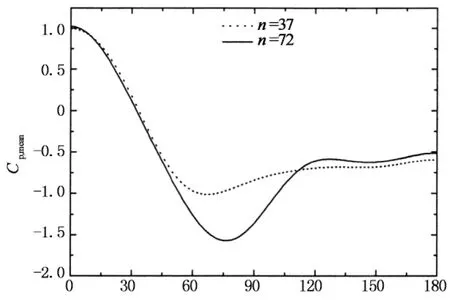
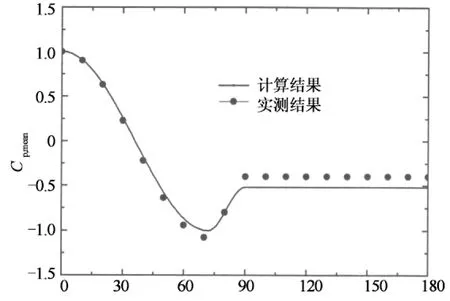
国内加肋塔较少，以文献[19]报导的德国Weisweiler塔为例，其外表面设有52条宽8 cm、高1.8 cm的子午向肋条，喉部直径为44.6 m，由此计算得到喉部的粗糙度系数k/s=0.067.由于它大于本次试验的最大粗糙度系数0.03，超出了式(3)的适用范围，故不能直接用该式计算Cpmin，但由图11(a)可知，当k/s>0.04后，最小负压系数Cpmin基本不变，约为-1.0，因此取Cpmin=-1.0，进而由式(4)可近似计算得到它的风压分布，计算结果与实测结果比较如图12所示，可以看出，二者除在背压区有点差异外(背压差异可能是由于塔型不同引起的，例如李鹏飞等的试验结果约为-0.50[20]、鲍侃袁的测试结果为-0.31[21]等)，其它圆周角处吻合良好，表明本文推荐的风压分布近似计算方法可以应用于指导实际冷却塔工程设计.

圆周角/(°)

6 结 论

本文通过刚性模型测压试验分析表面粗糙度对冷却塔风压分布的影响，得到以下主要结论：

1)粗糙条宽度b对风压分布影响较小，而粗糙条高度k和数量n影响较大，粗糙度系数k/s能较准确描述粗糙度大小；当k/s一致时，不同粗糙条数量n与高度k组合下的平均风压基本一致，但高度大的脉动风压小.

2)粗糙度对正压分布和背压大小影响较小，而负压区风压分布和背压稳定区宽度受它影响较大，其中以最小负压系数幅值最为显著；最小负压系数幅值、脉动风压系数峰值随粗糙度的增大而减小，背压稳定区宽度则略有扩大.

3)由于粗糙条能诱发边界层提前转捩，促使边界层由层流分离转变为湍流分离，通过增大模型表面粗糙度能有效地在较低雷诺数条件下实现高雷诺数下的平均风压分布，但脉动风压模拟的准确性有待大型冷却塔风压实测结果的验证.

[1] 邹云峰, 牛华伟, 陈政清. 基于完全气动弹性模型的冷却塔干扰效应风洞试验研究[J]. 湖南大学学报: 自然科学版, 2013, 40(12):1-7.

ZOU Yun-feng, NIU Hua-wei, CHEN Zheng-qing. Wind tunnel test on wind-induced interference effect of cooling towers based on full aero-elastic model[J]. Journal of Hunan University: Natural Sciences, 2013, 40(12):1-7.(In Chinese)

[2] 柯世堂, 候宪安, 姚友成, 等. 强风作用下大型双曲冷却塔风致振动参数分析[J]. 湖南大学学报: 自然科学版, 2013, 40(10):32-37.

KE Shi-tang, HOU Xian-an, YAO You-cheng,etal. Parameter analysis of wind-induced vibration for large hyperbolic cooling towers under strong wind loads[J]. Journal of Hunan University: Natural Sciences, 2013, 40(10):32-37. (In Chinese)

[3] NIEMANN H J, ZERNA W. Impact of research on development of large cooling towers[J]. Journal of Engineering Structures, 1986, 8: 74-86.

[4] 邹云峰, 牛华伟, 陈政清. 基于完全气动弹性模型的冷却塔风致响应风洞试验研究[J]. 建筑结构学报, 2013, 34(6):60-67.

ZOU Yun-feng, NIU Hua-wei, CHEN Zheng-qing. Wind tunnel test on wind-induced response of cooling tower based on full aero-elastic model[J]. Journal of Building Structures, 2013, 34(6):60-67. (In Chinese)

[5] ARMITT J. Eigenvector analysis of pressure fluctuations on the West Burton instrumented cooling tower[R]. London: Central Electricity Research Laboratories, 1968: 114-168.

[6] FARELL C, GUVEN O, MAISCH F. Mean wind loading on rough-walled cooling towers[J]. Journal of the Engineering Mechanics Division, ASCE, 1976, 102(6): 1059-1081.

[7] NIEMANN H J. Wind effects on cooling-tower shells[J]. Journal of the Structural Division, ASCE, 1980, 106(ST3): 643-661.

[8] 孙天风, 周良茂. 无肋双曲线型冷却塔风压分布的全尺寸测量和风洞研究[J]. 空气动力学学报, 1983, 4: 68-76.

SUN Tian-feng, ZHOU Liang-mao. A full-scale and wind-tunnel study of wind pressure distribution around a ribless hyperbolic cooling tower[J]. Acta Aerodynamica Sinica, 1983, 4: 68-76. (In Chinese)

[9] 刘天成, 赵林, 丁志斌. 圆形截面冷却塔不同表面粗糙度时绕流特性的试验研究[J]. 工业建筑, 2006, 36(增刊): 301-304.

LIU Tian-cheng, ZHAO Lin, DING Zhi-bin. Test research of flow feature for hyperbolic circular section cooling tower with different superficial roughness[J]. Industrial Construction, 2006, 36(S1): 301-304. (In Chinese)

[10]沈国辉, 余关鹏, 孙炳楠, 等. 模型表面粗糙度对冷却塔风荷载的影响[J]. 工程力学, 2011, 28(3): 86-93.

SHEN Guo-hui, YU Guan-peng, SUN Bing-nan,etal. The influence of modal surface roughness on wind loads of cooling towers[J]. Engineering Mechanics,2011, 28(3): 86-93. (In Chinese)

[11]董国朝, 陈政清, 罗建辉, 等. 冷却塔混凝土粗糙度对平均风压系数的影响[J]. 湖南大学学报:自然科学版, 2011, 38(7): 6-12.

DONG Guo-chao, CHEN Zheng-qing, LUO Jian-hui,etal. Effect of surface roughness on the mean pressure coefficient of concrete cooling tower[J]. Journal of Hunan University:Natural Sciences, 2011, 38(7): 6-12. (In Chinese)

[12]BURESTI G. The effect of surface roughness on the flow regime around circular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 8: 105-114.

[13]SHIH W C L, WANG C, COLES D,etal. Experiments on flow past rough circular cylinders at large Reynolds numbers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49: 351-368.

[14]操金鑫, 赵林, 葛耀君, 等. 双曲线圆截面建筑结构雷诺数效应模拟实践[J]. 实验流体力学, 2009, 25(4): 46-50.

CAO Jin-xin, ZHAO Lin, GE Yao-jun,etal. Practices on simulation of Reynolds number effects for the hyperbolic circular section structures[J]. Journal of Experiments in Fluid Mechanics, 2009, 25(4): 46-50. (In Chinese)

[15]SURRY D, DJAKOVICH D. Fluctuating pressures on models of tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 58: 81-112.

[16]邹云峰. 巨型冷却塔群的风效应及其风洞试验方法研究[D]. 长沙: 湖南大学土木工程学院, 2013: 29-34.

ZOU Yun-feng. Study on wind effects and wind-tunnel test method for super large cooling towers group[D]. Changsha:College of Civil Engineering, Hunan University, 2013:29-34. (In Chinese)

[17]RIBEIRO J L D. Effects of surface roughness on the two-dimensional flow past circular cylinders Ⅱ: fluctuating forces and pressures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1991, 37: 311-326.

[18]YEUNG W W H. Similarity study on mean pressure distribution of cylindrical and spherical bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95: 253-266.

[19]NIEMANN H J. Wind pressure measurements on cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1973, 1: 265-281.

[20]李鹏飞, 赵林, 葛耀君, 等. 超大型冷却塔风荷载特性风洞试验研究[J]. 工程力学, 2008, 25(6): 60-67.

LI Peng-fei, ZHAO Lin, GE Yao-jun,etal. Investigation on wind load characteristics for super large cooling tower in wind tunnel[J]. Engineering Mechanics, 2008, 25(6): 60-67. (In Chinese)

[21]鲍侃袁. 大型双曲冷却塔的风荷载和风致响应理论分析与试验研究[D]. 杭州: 浙江大学建筑工程学院, 2009: 33-36.

BAO Kan-yuan. Theory analysis and experimental study on wind load and wind-induced response for large hyperbolic cooling tower[D]. Hangzhou: Department of Civil Engineering,Zhejiang University, 2009: 33-36. (In Chinese)

Influence of Modal Surface Roughness on Wind Pressure Distribution of Hyperbolic Cooling Tower

ZOU Yun-feng1,2,3, HE Xu-hui1,2†, WANG Han-feng1,2, TAN Li-xin3, NIU Hua-wei4

(1．School of Civil Engineering, Central South Univ, Changsha, Hunan 410075, China;2．National Engineering Laboratory for High Speed Railway Construction, Changsha, Hunan 410075, China;3．China Construction Fifth Engineering Division Co Ltd., Changsha, Hunan 410004, China;4．Wind Engineering Research Center， Hunan Univ, Changsha, Hunan 410082, China)

The wind pressure distribution of cooling towers with different rough strip parameters was tested, and the influence of roughness on both mean and fluctuating wind pressure was investigated. The experiment results show that the width of rough strip has little effect on the distribution of wind pressure, while the height and number have a greater impact, and the roughness coefficientk/scan describe the size of roughness accurately. Even though the numbernand heightkof rough strip is different, as long as the roughness coefficientk/sis consistent, the mean pressure distribution is basically the same, but the peak fluctuating pressure is smaller with higher height of rough strip. Furthermore, roughness has little effect on both the distribution of positive pressure and the size of back pressure. However, the amplitude of the smallest negative pressure coefficient and the peak fluctuating pressure decrease with the increase of roughness, while the width of back pressure expands slightly. Although the mean pressure at high Reynolds number can be simulated effectively at low Reynolds number by increasing surface roughness, the simulation accuracy of fluctuating pressure should be checked with field tests in the future.

cooling tower; surface roughness; wind pressure distribution; wind tunnel test

1674-2974(2015)07-0016-09

2014-09-10

国家自然科学基金资助项目(51178471,51322808) ,National Natural Science Foundation of China(51178471,51322808) ；中国博士后科学基金资助项目(2014M562133); 教育部新世纪优秀人才支持计划(NCET-12-0550)

邹云峰(1984-)，男，湖南邵阳人，中南大学讲师，博士

†通讯联系人，E-mail:xuhuihe@csu.edu.cn

TU311.3；V211.7

A