基于粒子群算法的隐式广义预测在ATO中的应用

马宝峰，路小娟

(兰州交通大学自动化与电气工程学院， 兰州　730070)

qq.com。

基于粒子群算法的隐式广义预测在ATO中的应用

马宝峰，路小娟

(兰州交通大学自动化与电气工程学院， 兰州730070)

摘要：由于列车运行速度的不断提高，对列车自动驾驶(Automatic Train Operation， ATO)系统提出更高的要求。针对隐式广义预测(Implicit Generalized Predictive Control， IGPC)控制器在ATO中难以获得最优预测控制输入的问题，运用一种基于粒子群优化(Particle Swarm Optimization， PSO)的IGPC算法对ATO系统进行控制。为更进一步提高PSO算法的寻优能力，对基本PSO算法进行改进，从而有效提高系统的寻优精度和速度。并对有约束情况下的CRp型车进行仿真验证，仿真结果显示PSO-IGPC比单纯IGPC对ATO的控制效果更优。

关键词：列车自动驾驶；隐式广义预测控制算法；粒子群优化算法；仿真

我国高速铁路目前通过采用列车速度防护技术，实现了列车运行速度的实时监控，有效防止了人为误操作事故的发生，列车行驶的安全性得到了有效保障。通过国内近几年高速铁路的不断发展，列车自动驾驶(Automatic Train Operation， ATO)系统将是高速铁路列车控制系统发展趋势之一[1]。

国内大多数的ATO系统仍采用PID控制[2]，其优点在于原理简单，容易实现。但由于其切换过于频繁而不利于列车的平稳运行；后来学者相继提出了将模糊控制、神经网络控制、专家系统控制等智能控制方法用在ATO系统中来，均取得了较好的控制效果，但由于模糊控制和专家系统控制很大程度上依赖于人的经验，给实际应用带来了一定困难；而对于神经网络控制在ATO中的应用，其自学能力强，但不能解释其具体的推理过程[3-5]。

隐式广义预测控制(Implicit Generalized Predictive Control， IGPC)算法是在基本广义预测控制(GPC)算法的基础上发展而来的，其计算速度更快，控制效果更好。IGPC具有较强的鲁棒性、自适应和自校正能力，对模型精度要求不高等优点，能很好地适用于时滞性、非线性系统。ATO过程具有非线性、时滞性的特征，并且极易受环境因素的影响，难以建立精确的数学模型。所以IGPC算法是适用于列车自动驾驶系统的，但在利用IGPC梯度寻优时的ATO系统是假设线性无约束的。为了提高IGPC对ATO的控制性能，必须找到一种能克服IGPC在约束情况下的寻优方法[6-7]。

针对上述问题，本文应用一种基于粒子群优化(Particle Swarm Optimization， PSO)的IGPC混合控制算法。由于PSO算法模型简单、易于实现，并能以较大概率快速求得全局最优解。所以应用PSO算法优化IGPC算法，能更好地寻优到最优控制增量，有效提高列车的鲁棒性，改善IGPC算法对ATO的控制性能。

1隐式广义预测控制算法

1.1广义预测控制1.1.1预测模型

CARIMA模型作为GPC的预测模型[8]

(1)

式中，A(z-1)、B(z-1)、C(z-1)分别为z-1的多项式；Δ=1-z-1为差分算子；ξ(k)表示均值为零的白噪声序列，y(k)表示系统输出，u(k)表示系统输入。

1.1.2预测输出

针对CARIMA模型引入丢番图Dioaphantine方程[9]进行求解

(2)

式中Ej(z-1)=1+ej，1z-1+…+ej，j-1z-(j-1)

Fj(z-1)=fj，0+fj，1z-1+…+fj，nz-n

结合丢番图方程和CARIMA模型，假设C(z-1)=1，利用k时刻系统输入、输出数据，对k+j时刻的系统输出进行预测，在忽略未来白噪声对系统输出影响的情况下可得到j步后的预测输出值为

(3)

式中

(4)

多步输出预测值的矢量表示形式

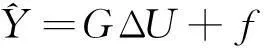
(5)

式中

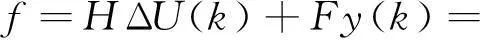
1.1.3滚动优化

在GPC算法中，优化性能指标必须实现系统输出误差及控制加权项最小化。

(6)

式中，w(k+j)=αjy(k)+(1-αj)yr(k)，yr为设定值，0≤α<1，m、n分别为控制步长和预测步长(m≤n)；λ(j)为控制加权系数；Δu(k)为系统控制增量；因此，性能指标式(6)在无约束情况下利用梯度寻优法可计算得到控制增量最优解：

(7)

最优控制输入为

(8)

式中,gT为矩阵(GTG+λI)-1GT的第一行矢量。

1.2隐式广义预测控制算法

由最优控制律式(7)可知，在求ΔU时必须先求得矩阵G和开环预测向量f，隐式自校正方法就是利用输入输出数据，根据预测直接辩识矩阵G和f。

根据式(5)可得n个并列预测器为

(9)

由式(9)可得，矩阵G中的所有元素都在最后一个方程中出现，因此对最后一个方程辨识即可得到矩阵G。式(9)最后一个方程可以写为如下形式

(10)

式(10)中：

根据最小二乘递推法[10]可得到矩阵G中的元素g0，g1，…，gn-1和f(k+n)。

2粒子群算法概要

PSO算法[11-12]是近年来发展起来的一种新的进化算法。PSO算法通过随机初始化种群粒子迭代搜寻最优解。每一次迭代中，粒子通过跟踪个体最优解和种群最优解来更新自己。粒子根据如下公式来更新自己的速度和位置

v(t+1)=wv(t)+c1r1(pbest(t)-x(t))+

(11)

(12)

式(11)、式(12)中，x(t)、v(t)分别表示t时刻粒子的位置和速度；pbest(t)、gbest(t)分别为粒子的个体极值和种群的全局极值；w为惯性权重；c1、c2为加速因子；r1、r2是在[0，1]范围内变化的随机数。

由于PSO算法模型简单，易于实现，收敛速度快，精度较高等优点而得到了广泛应用。

3粒子群混合优化的隐式广义预测控制器

本文在IGPC算法的滚动优化环节中引入PSO算法，来与IGPC无约束情况下的梯度寻优相互配合，构成一种多模态混合优化方法。当被控对象无约束时使用梯度寻优获得最优控制输入量，当存在约束时，梯度寻优与PSO相互配合，快速而精确地获得系统最优控制输入。控制结构如图1所示。

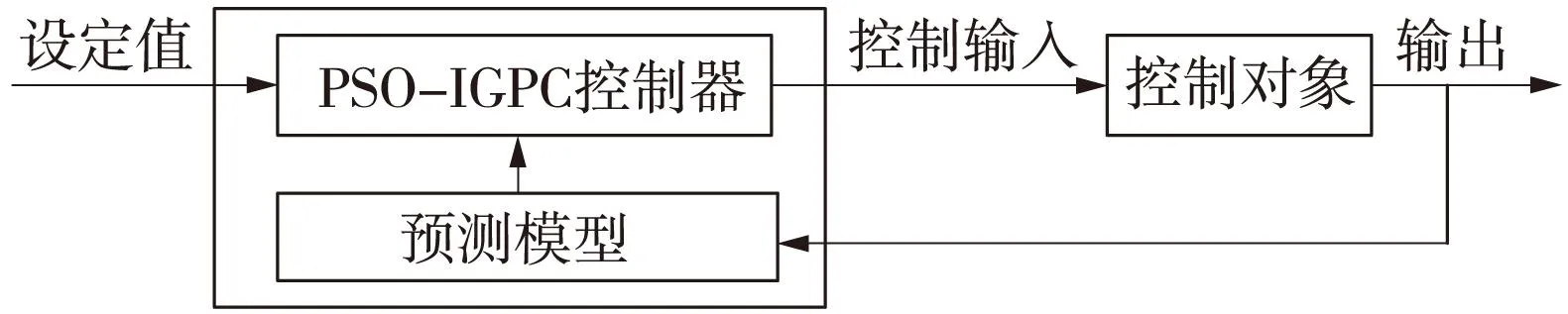
图1　PSO-IGPC控制结构

3.1PSO-IGPC寻优策略设置

在跟随目标变化不大或者不变时采用IGPC算法完全可以满足应用要求，可以达到很好的跟随效果，但在跟随对象变化较大时，就需要IGPC算法与PSO算法相结合，以获得系统最优控制输入。

在PSO-IGPC寻优中，首先将IGPC寻优所得的控制增量选出一部分，并将超出约束条件的部分按限定边界值设定，初始化时将IGPC优化得到ΔU赋值给初始化种子的θ%，剩余种子随机赋给初值。这既保证了种群多样性的同时又使种群含有部分优质种子，增加了算法的快速性。寻优流程图如图2所示。

图2　PSO-IGPC寻优流程

在优化控制中，为使控制输入增量ΔU变化更小，提高系统的鲁棒性，采用式(6)作为PSO算法的适应度函数，优化目标值为0。PSO算法寻优环节为了提高寻优速度和寻优精度通常设置一个最大稳定连续迭代次数b和稳定精度δ两个参数，用来判断算法是否已获得最优值，只要达到其中一个参数则终止寻优。这样既提高了寻优的实时性，同时又节省了寻优时间。

3.2PSO-IGPC速度控制器的设计

本文根据PSO-IGPC算法原理、机车特点设计的速度控制器如图3所示。在PSO-IGPC控制器中，目标曲线经柔化调节后作为参考轨迹输入给控制器，使列车跟随目标曲线时的超调量得到进一步控制。控制器检测到列车实际输出速度与预测速度的偏差后反馈给系统，对下一时刻的预测进行修正，最终达到预测输出与实际输出偏差为零或很小。其优点在于对模型精度要求不高，对不易建立精确数学模型的ATO系统更具现实意义。

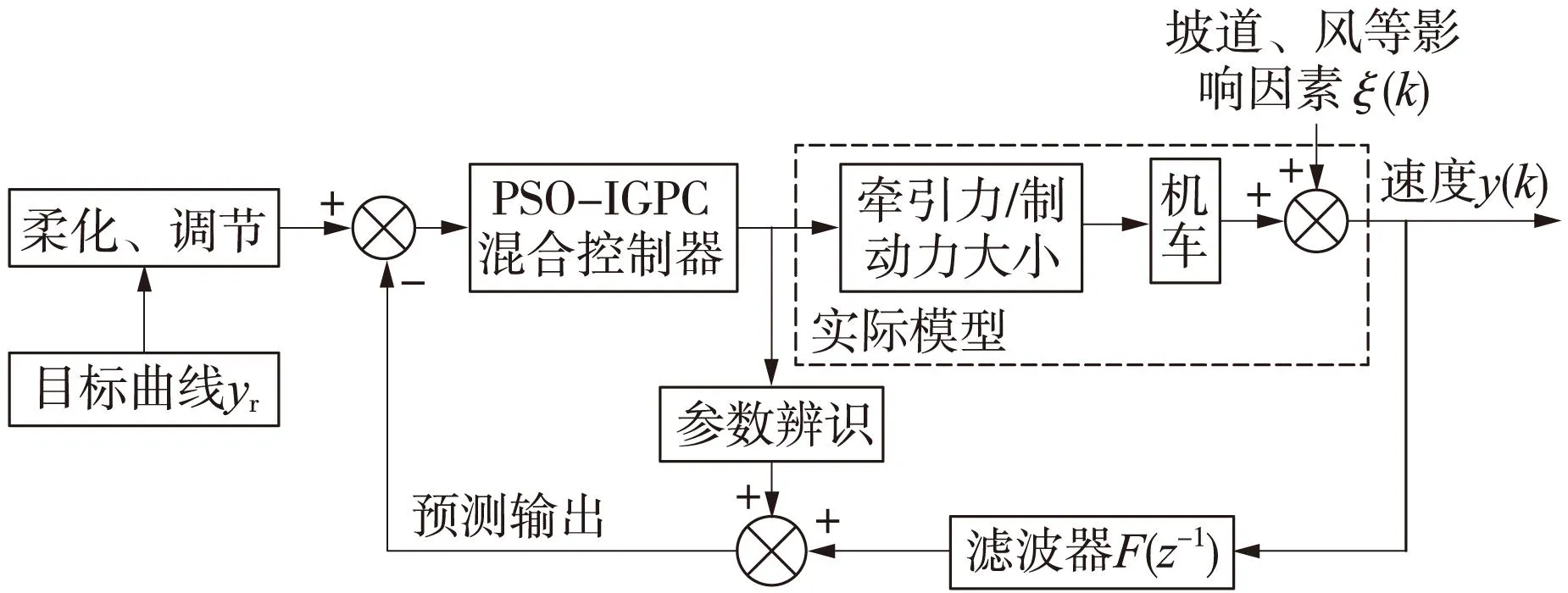
图3　PSO-IGPC速度控制器的设计

4仿真结果分析

4.1列车模型确定

本文的控制对象参考文献[13]中的列车模型，如式(13)所示。

(13)

该模型有12个控制级位作为系统输入，牵引力与列车级位关系为c/d=1 800，得到列车实际制动力和牵引力。列车实际运行速度作为系统输出。设定采样周期T=0.5 s，式(13)的列车运动模型转换成差分方程为

y(k+1)=0.797y(k)+0.992 7y(k-1)-

0.804 3y(k-2)+0.008 29u(k)+0.016u(k-

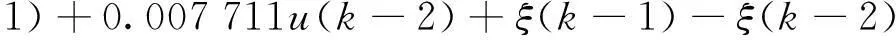
(14)

式中，ξ(k-1)、ξ(k-2)分别为k-1与k-2时刻的干扰量。

4.2列车目标曲线的生成

由于列车保持匀速行驶或惰性行驶时均能减少能量损耗，因此，在生成目标曲线时使列车按照加速-匀速-惰性-匀速-惰性-制动停车工况进行转换，以达到节能目的。速度控制器控制列车跟随目标曲线进行行驶，使列车达到节能的目的。

本文在仿真中采用CRp型车，参照列车牵引特性曲线[14]，用曲线拟合法，将文献[14]中的列车牵引力与速度的关系近似看作2条一次函数的曲线组成。结合表1所示的列车参数，得到列车单位牵引力f与速度v的关系，如式(15)所示。

(15)

对于CHR2型列车在制动工况下，其制动减速度由表2所给定的数据得到。在仿真时考虑到采取节能模式，本文中采用7N档的减速度。

表1　CRp型列车参数

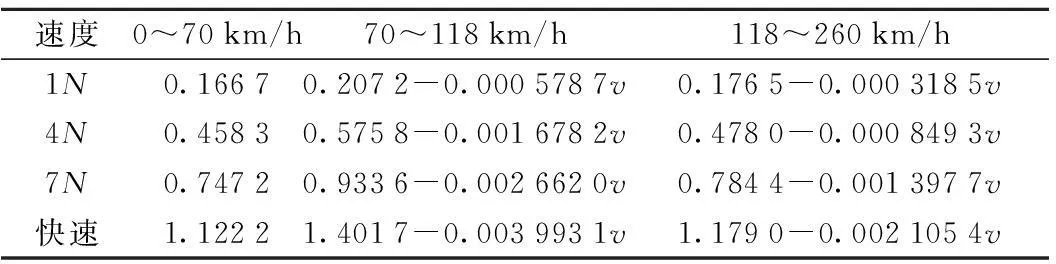
表2　CRp型动车组制动减速度　m/s2

本文设定列车进出站的运行速度为75 km/h，站台路程为1 300 m，区间限速下的最大运行速度应稍低于列车自动防护系统给定的限定速度，本文取230 km/h，列车的运行目标速度为225 km/h。目标曲线如图4、图5所示。

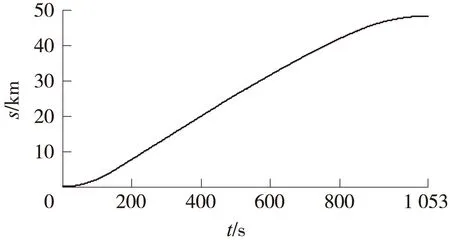
图4　t-s目标曲线

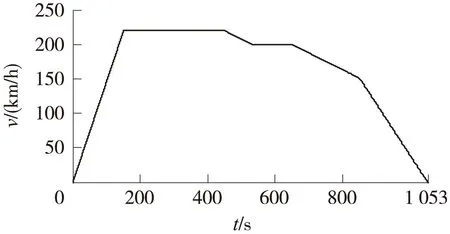
图5　t-v目标曲线

4.3PSO-IGPC控制器仿真

本文以Matlab7.0为平台进行仿真，以优化的目标曲线作为系统输入，先后由IGPC控制器及PSO-IGPC控制器对目标曲线进行跟随，仿真过程中各参数分别取c1=2，c2=2，ΔU∈[-35，35]，n=6，m=2，λ=0.9，α=0.3，w=0.6，b=1 000，θ=30，δ=0.01。

由图6可以看出，IGPC控制器在PSO算法的优化下提高了系统跟随的快速性，减小了跟随误差，提高了跟随精度。

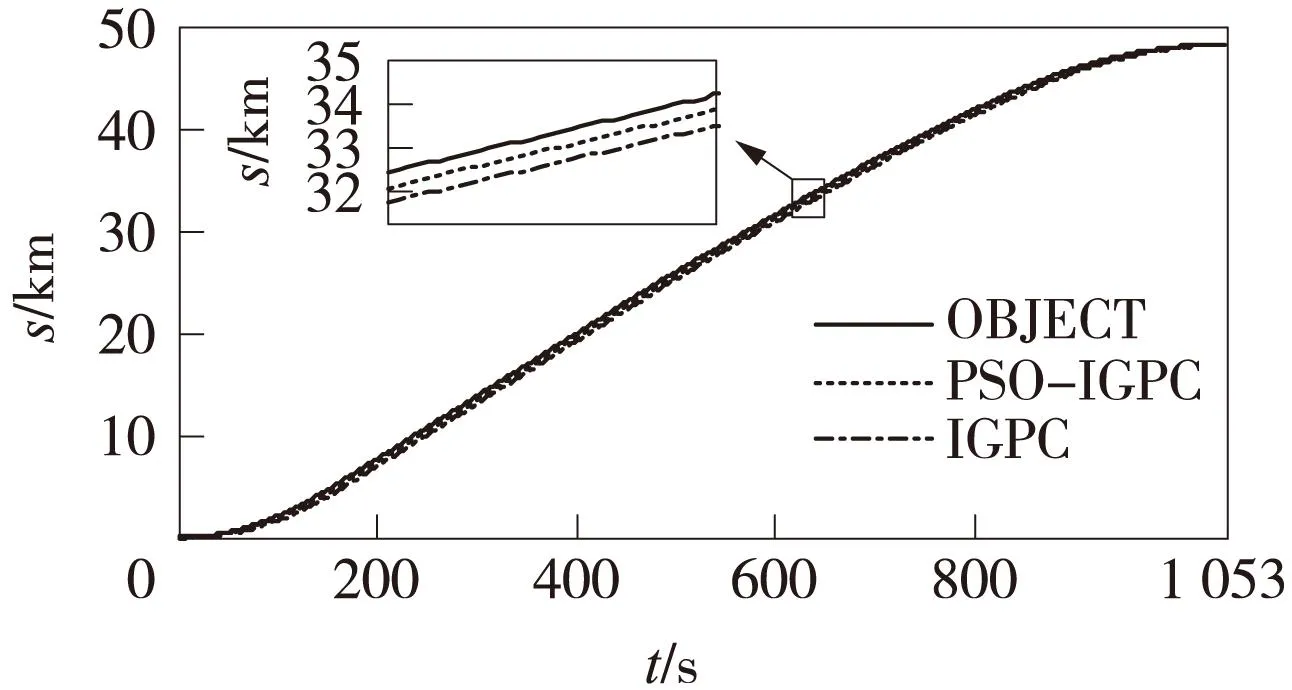
图6　t-s仿真曲线

图7为v-t跟随仿真曲线，对应其跟随误差如图8所示，PSO-IGPC控制器误差明显较低，并且变化幅度更小，相对于IGPC控制器更有利于ATO控制。

图7　v-t仿真曲线

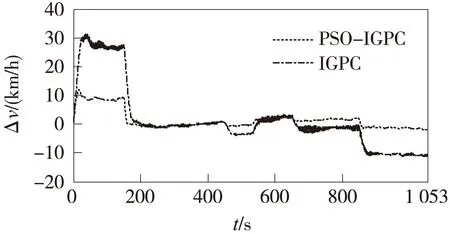
图8　v-t跟随误差分析

目标曲线持续变化时，为增强列车运行的鲁棒性，提高乘客的舒适度，本文设置一定的控制增量变化范围。在铁路设计当中[15-16]，加加速度表现为列车的颤力，抖动程度的物理量，其极限值应小于2 m·s-3，换算为单位牵引力变化率等于200 N/(kN·s)， 通常列车单位牵引力变化率应小于200 N/(kN·s)，否则会让乘客难以忍受，从而影响乘客舒适度。本文设定单位牵引力变化率ΔU介于-30 N/(kN·s)与80 N/(kN·s)之间。由图9可以看出，在PSO-IGPC控制器的控制下，波动明显小于IGPC控制器，有效提高了列车的鲁棒性和乘客的舒适度。所以，将PSO-IGPC控制器应用于ATO系统中具有更好的控制效果。

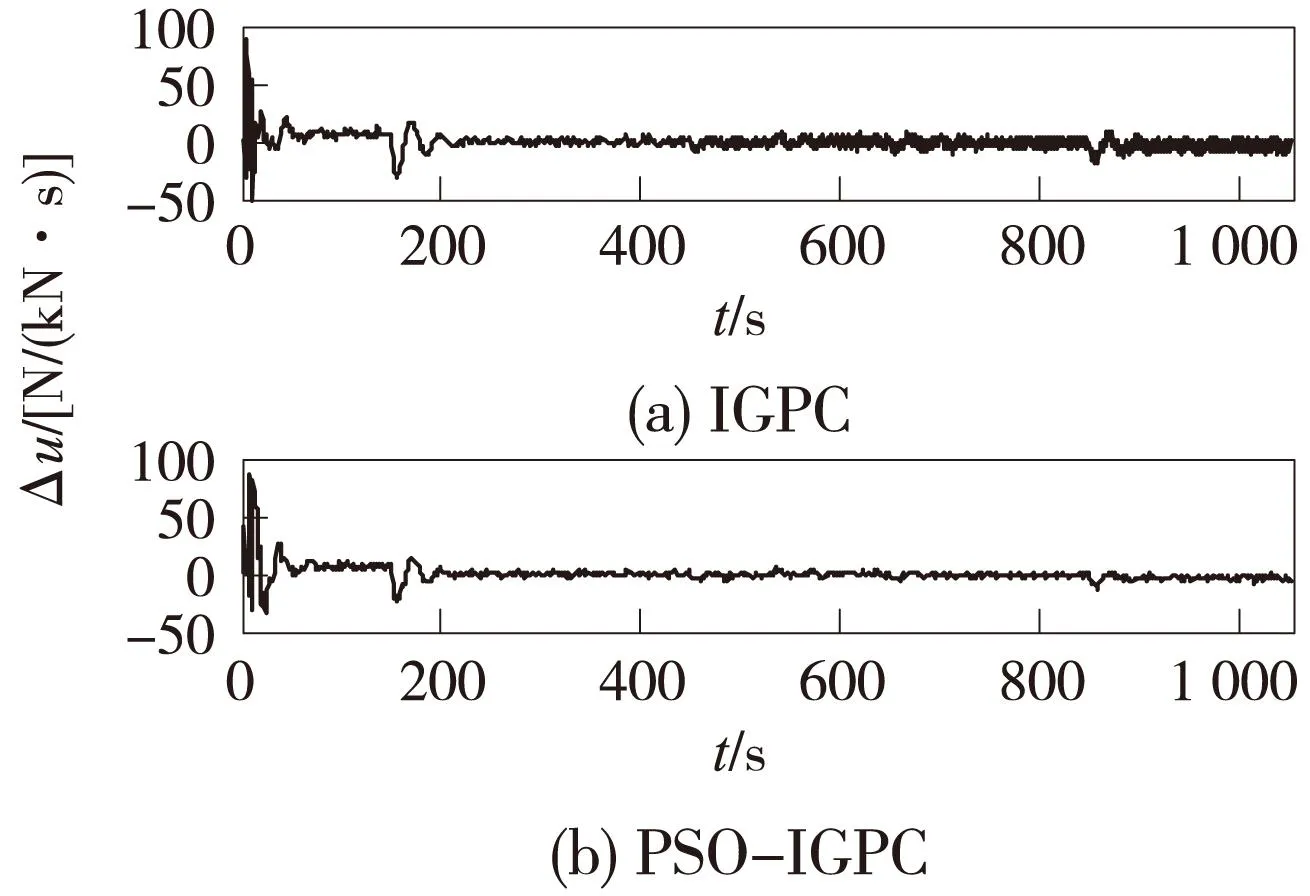
图9　v-t控制增量对比

5结语

本文针对ATO系统的优化问题，利用PSO算法和IGPC算法各自的优点，提出了采用PSO算法优化IGPC控制器来控制ATO系统，从而有效提高了列车的控制性能和控制精度，对在有约束情况下的列车自动调速过程进行了仿真验证，仿真结果显示在采取节能策略的基础上其寻优速度更快、更精确、跟随性能更好，控制增量变化波动更小，鲁棒性更强，从而使列车的运行更安全、更平稳、更节能、更准时。

参考文献：

[1] 杨罡，刘明光，喻乐.高速列车运行过程的非线性预测控制[J].铁道学报，2013，35(8):16-21.

[2]唐涛，黄良骥.列车自动驾驶系统控制算法综述[J].铁道学报，2003，25(2):98-102.

[3]Kurioka H，Oka Y，Satoh H，etal.Fire properties in near field of square fire source with longitudinal ventilation in tunnels[J].Fire Safety Journal，2003，38(4):319.

[4]陈晶.基于GA模糊神经网络的列车自动驾驶优化研究[D].兰州：兰州交通大学，2013.

[5]Jojo S M， W.K C. Numerical studies on performance evaluation of tunnel ventilation safety systems[J]. Tunnelling and Underground Space Technology， 2003，18(5):435.

[6]Guzman J L， Berenguel M， Dormido S. Interactive teaching of constrained generalized predictive control[J]. Control Systems Magazine， IEEE(S0272-1708)， 2005，25(2):52-66.

[7]Olaru S， Dumur D. Feasibility of constrained generalized predictive control within invariant sets framework[C]//5th IEEE Asian Control Conference ASCC’04， Melbourne， Australia. 2004.

[8]王伟.广义预测控制理论及其应用[M].北京:科学出版社，1998:1-18.

[9]陈晓化.几类丢番图方程的研究[D].西安：西北大学，2009.

[10]邹乐强.最小二乘法原理及其简单应用[J].科技信息，2010(23):282-283.

[11]Zou Leqiang. The theory and simple application of The least square method[J]. Science and Technology Information， 2010(23):282-283.

[12]刘建华.粒子群算法的基本理论及其改进研究[D].长沙：中南大学，2009.

[13]Shi Y H，Eberhart R C. A Modified Particle Swarm Optimizer[C]∥IEEE International Conference of Evolutionary Computation，Anchorage， Alaska: 1998.

[14]刘智勇.高速磁浮列车安全速度曲线算法及紧急制动控制研究[D].杭州:浙江大学，2008.

[15]周峰.动车组牵引计算建模及软件仿真[D].成都:西南交通大学，2007.

[16]董水金，佘守宪.关于加加速度的若干机械运动分析及MATLAB模拟[J].大学物理，2005，24(2):57-62.

[17]孟昭曜.加加速度的力学计算和物理意义[J].四川师范大学学报，2005，28(6):741-743.

Application of Implicit Generalized Prediction Based on Particle Swarm Optimization algorithm in ATO

MA Bao-feng， LU Xiao-juan

(School of Automation and Electrical Engineering， Lanzhou Jiaotong University， Lanzhou 730070， China)

Abstract：The continuous increase of train speed sets higher requirements for the Automatic Train Operation (ATO) system. As it is difficult to obtain the optimal predictive control input for the implicit generalized predictive controller in the automatic train operation， this paper applies an IGPC algorithm based on Particle Swarm Optimization (PSO) to control the ATO system. In order to further optimize PSO， the basic PSO algorithm is improved， thus effectively improving the accuracy and speed of searching optimization. The CHR2 trains are simulated and verified under constrained conditions. The simulation results show that PSO-IGPC has a better effect than simple IGPC control for ATO.

Key words：Automatic train operation; Implicit generalized predictive control algorithm; Particle swarm optimization algorithm; simulation

中图分类号：TP273

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2015.06.032

文章编号：1004-2954(2015)06-0143-05

作者简介：马宝峰(1986—)，男，硕士研究生，E-mail：1172524908@

基金项目：甘肃省自然科学基金(1208RJZA180)

收稿日期：2014-08-27； 修回日期：2014-09-20