基于变权欧氏距离关系度的采空区稳定性评价

路 凡，罗周全，马红贝，冯雪飞

(中南大学资源与安全工程学院，湖南长沙 410083)

0引言

随着我国金属矿山的不断开采，采空区已成为影响金属矿山安全生产的重大危险源之一［1］。国内外学者在对采空区稳定性进行评价时主要分为定性评价与定量评价两种，评价方法较多，如神经网络［2］、突变级数法［3］、模糊综合评价［4］、数值模拟分析［5］、概率积分法［6］、层次分析法［7］。这些方法考虑了采空区的各种不确定因素及其复杂性，从主观或客观上评价了采空区的稳定性情况。现有评价方法虽然考虑了不同指标在同等条件下对采空区稳定性的影响，但没有考虑同一个指标的不同数值对采空区稳定性的影响程度;所以评价结果通常只能给出采空区稳定性等级，不能评价出采空区所在稳定性等级的优劣。

欧式距离是聚类分析中常用的术语，考虑不同因素的影响程度不同对欧氏距离赋予权重，则变成加权欧式距离。考虑影响因素权重的变化，则成为变权欧式距离模型。变权欧式距离模型曾经在水质评价［8］、边坡稳定性评价［9］、地下洞室岩体质量评价［10］中得到应用。采空区稳定性是一个多属性的集合体，不同评价指标对采空区稳定性影响程度不同，且同一指标在不同数值下对采空区稳定性影响程度不同。使用变权欧式距离将各个评价指标规范化，确定各稳定等级的满意点，以采空区稳定性等级I级的下限值作为稳定性的“原点”，结合采空区各评价指标规范化权重值计算得到采空区的变权欧氏距离，以此对采空区稳定性进行评价。

1 采空区评价指标

采空区稳定性影响因素较多，通过相关文献资料［11-12］，并结合大量的工程实例，确定影响采空区稳定性的因素主要有水文地质因素、环境因素、采空区几何参数3方面、14个类别。具体归纳如下:

(1)水文地质因素:岩体结构B1、岩石质量指标B2、地质结构B3、地下水B4、地下可见水对围岩的影响B5;

(2)环境因素:周围开采影响 B6、相邻空区情况B7;

(3)采空区几何参数:跨度B8、面积B9、高度B10、矿柱尺寸布置B11、埋藏深度B12、跨高比B13、工程布置B14。

一般将采空区的稳定性分为稳定(Ⅰ级)、较稳定(Ⅱ级)、不稳定(Ⅲ级)和极不稳定(Ⅳ级)4个等级，上述14个评价指标各评价指标的分级与取值见表1。

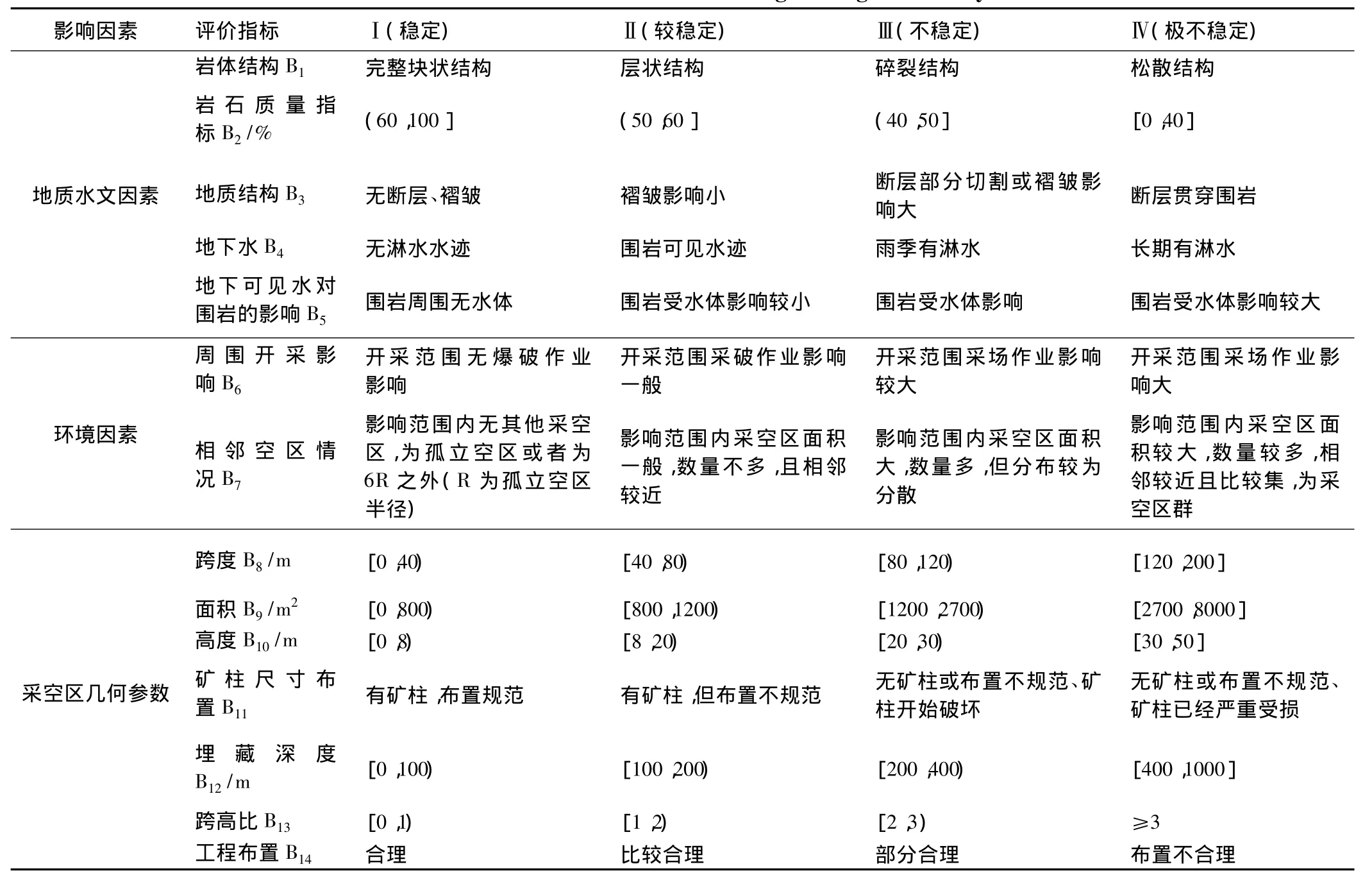
表1 采空区稳定性评价的指标分级标准Table 1 Classification criterion of indexes underground goaf stability evaluation

为了使不同量纲的评价指标具有可比性，需对评价指标进行无量纲化处理。评价指标按其作用不同，可以分为正向指标和逆向指标。正向指标是指标数值越小，采空区稳定性越差的一类指标，逆向指标则是指其数值越大，采空区稳定性越差的评价指标。两种指标的无量纲化处理方式如下所示:

(1)正向指标

(2)逆向指标

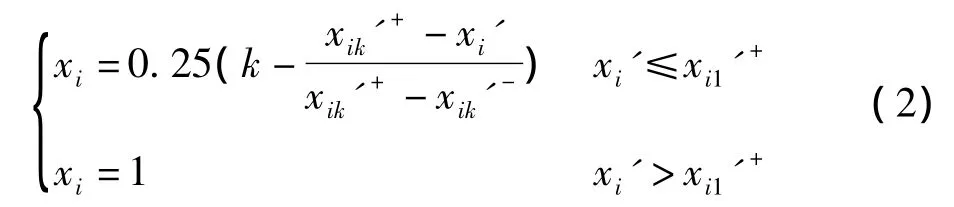
式中:xi——评价指标标准值，i=1，2，…，n;

k——采空区稳定等级，k=1，2，3，4;

xi'——评价指标数值;

xik'+——k等级区间的最大值;

xik'-——k等级区间的最小值。

根据公式(1)和公式(2)可计算出标准化的采空区稳定性评价指标和分级标准(表2)。

表2 标准化的采空区稳定性评价指标和分级标准Table 2 Evaluation indicators and grading standards of underground goaf stability after standardization

2 变权欧氏距离关系度的原理及步骤

由于不同因素对采空区稳定性的影响不同，应用欧氏距离理想点法时必须考虑不同指标的重要性，即权重。为了准确确定指标的权重值，主要从两个方面进行考虑，一是不同因素对采空区稳定性的影响程度，可用模糊物元法确定;二是同一指标的不同数值对采空区稳定性的影响程度，可以用变权欧氏公式表达。因此，变权欧氏距离理想点法的具体步骤如下:

2.1 建立欧氏评价指标空间矩阵

对于一个评价对象C，xi表示第i个评价指标的取值;wi表示第i个评价指标的权重。则评价对象C的评价指标矩阵表达如下:

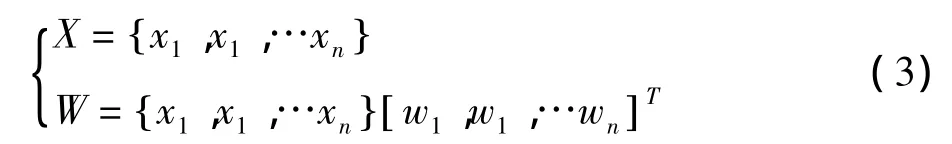
2.2 权重的确定

首先，采用模糊物元法确定指标的权重w(0)i，w(0)i反映了不同指标在同等条件下对评价对象的影响程度。其次，由于同一个指标的不同数值对采空区稳定性的影响程度不同，以动态权重体现相同指标在不同取值下对采空区稳定性更科学，引入均衡函数的变权公式［13］表示，即:

式中:a——变权类型控制系数，若0≤a＜1;

wi——惩罚型变权，只要某个指标取值过小综合评价值也将变小。

若a=1，wi为常权;当a＞1时，wi为激励型变权，综合评价中只要有一个指标值取值非常大，综合评价值迅速增大。

对于采空区稳定性评价，标准化后，评价指标数值越大，对采空区稳定性的影响程度越大，因此采用激励型变权，其中a取1.5。

2.3 确定满意点

满意点的确定受评价指标类型的影响。对正向指标，指标数值越大越好;对逆向指标，指标数值越小越好。若在取值范围内，评价指标呈线性变化，具体表示如下:

(1)正向指标:

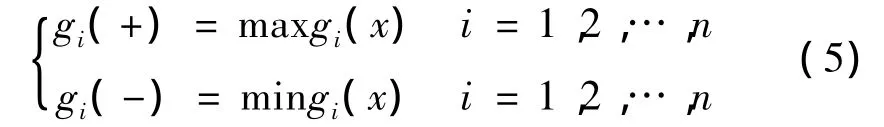
(2)逆向指标:

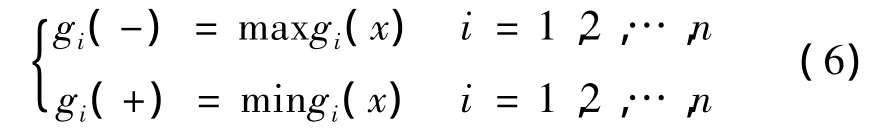
式中:gi(+)——表示为第i个评价指标所在等级的满意点;

gi(-)——表示第i个评价指标所在等级的差点;

gi(x)——表示xi的指标取值。

2.4 变权欧氏距离评价函数

对于任何一个评价指标xi，越是接近满意点，则评价对象C在等级的稳定性越好。反之，则稳定性越差。引入欧氏距离法［14］表示满意点和差点的距离，表示如下:

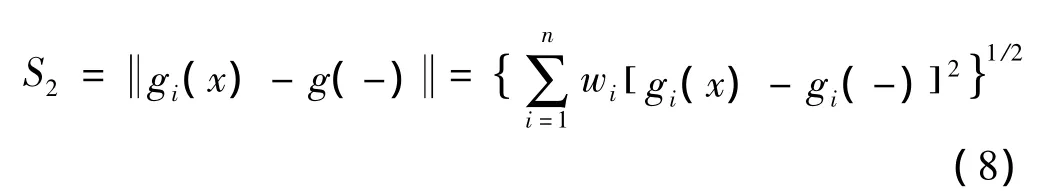
2.5 满意点关系度

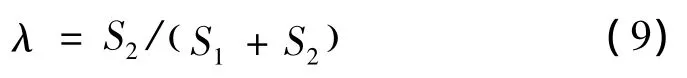
由公式(9)可知，若满意点关系度λ越小，则表示评价指标离满意点越近，离差点越远。

2.6 稳定性综合评价分级

采空区满意点关系度可以综合的反映采空区的稳定性情况，但是不能表示所在等级的稳定性程度。对于采空区，即使在同一稳定性级别，稳定性也存在着较大的差别。因此有必要对评价指标在所属稳定性等级内进一步细化。将各评价指标所属稳定性等级的上下限作为关系度稳定性综合评价分级的标准，具体如下:

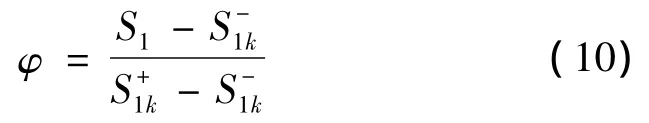
若0≤φ ＜1/3，则k级偏好;若1/3≤φ ＜2/3，则k级;若2/3≤φ≤1，则k级偏差。

3 工程实例分析

3.1 评价指标标准化

以某地下金属矿8个采空区为例，采用变权欧氏距离满意点进行稳定性评价，评价指标如表3。

需要说明的是，对于采空区的定性指标，Ⅰ(稳定)赋值1;Ⅱ(较稳定)赋值2;Ⅲ(不稳定)赋值3;Ⅳ(极不稳定)赋值4。

根据公式(1)、(2)对各评价指标进行标准化处理，结果见表4。

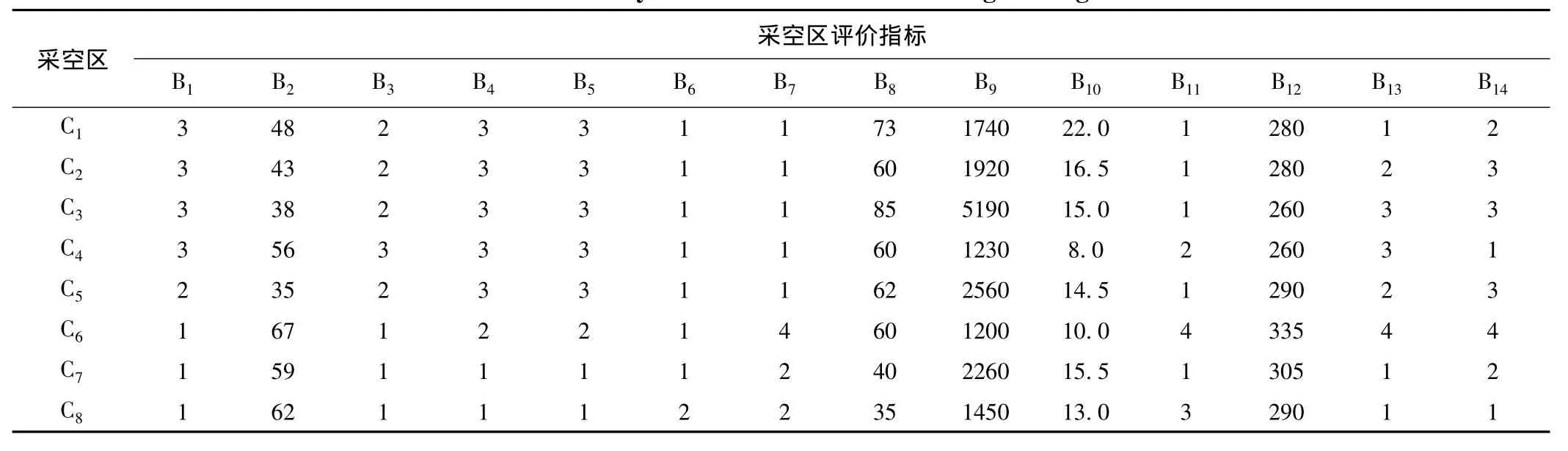
表3 采空区稳定性评价指标Table 3 Stability evaluation indexes of underground goaf

表4 标准化的采空区稳定性指标数值Table 4 Standardized values of indicators of underground goaf stability

3.2 确定权重

采用模糊物元法［15］计算出采空区各评价指标的权重，结果为按公式(4)计算出各采空区的欧氏距离的变权权重，结果见表5。

3.3 采空区的变权欧氏距离与评价

以往确定满意点时，都是以各评价指标的分界值作为满意点集合，但是这种方法存在评价的标准不统一，所得满意点关系度不可比的问题，结果也往往与实际不相符，因此需将满意点进行统一［16］。采空区各标准进行标准化之后，都属于逆向指标，因此将Ⅰ(稳定)的下限值作为满意点，将Ⅳ(极不稳定)的上限值作为差点，即:

根据式(7)～(11)计算各采空区对应的满意点关系，从而进一步进而确定各指标稳定性综合评价分级，具体结果见表6。

表5 采空区稳定性指标变权权重Table 5 Alterable weights of underground goaf stability indexes

表6 各采空区的变权欧氏距离与评价Table 6 The Euclidean distances with varying weights and the evaluation of each underground goaf

由表6可知，C3稳定性等级最差，偏向于极不稳定采空区;C2、C4、C5、C1属于不稳定采空区，但是 C1的稳定性相对较好;C7、C8属于稳定性采空区，根据变权欧氏距离可知C7的稳定性优于C8;C6的稳定性最优，偏向于极稳定采空区。变权欧氏距离关系度与实际情况相符。

4结论

应用变权欧氏距离关系度对工程实例进行了分析，验证了变权欧氏距离满意点在采空区稳定性评价中的有效性。变权欧氏距离关系度模型在使用过程中具有下列优点:

(1)对欧氏距离赋予权重，考虑了同一个指标的不同数值对采空区稳定性的影响程度不同，以动态权重体现相同指标在不同取值下对采空区稳定性的影响，使得评价结果更有效;各采空区的稳定性以变权欧式距离为度量值，评价结果更形象、直观;

(2)以采空区稳定性等级Ⅰ级的下限值作为满意点，即变权欧氏距离的“原点”，使评价结果更具有统一性;引入关系度，可以评价在同一等级下采空区的稳定性情况，进而对采空区进行稳定性综合评价分级。

［1］罗周全，杨彪，刘晓明，等.基于CMS实测及Midas-FLAC3D耦合的复杂空区群稳定性分析［J］.矿冶工程，2010，30(6):1-5.LUO Zhouquan，YANG Biao，LIU Xiaoming，et al.Stability analysis for goaf group based on CMS and coupling of Midas-FLAC3D［J］. Mining and Metallurgical Engineering，2010，30(6):1-5.

［2］汪伟，罗周全，王益伟，等.金属矿山采空区危险性辨识的遗传BP模型研究［J］.中国安全科学学报，2013，23(2):39-44.WANG Wei，LUO Zhouquan，WANG Yiwei，et al.Study on genetic BP godel for identifying metal mine goaf danger ［J］.China Safety Science Journal，2013，23(2):39-44.

［3］陈娇，罗周全，侯造水.基于改进突变级数法的金属矿采空区稳定性评价［J］.中国安全生产科学技术，2013，9(11):17-24.CHEN Jiao，LUO Zhouquan，HOU Zaoshui.Stability evaluation of metal mine goaf based on improved catastrophe progression method ［J］.Journal of Safety Science and Technology，2013，9(11):17-24.

［4］朱为民，李想，陈国梁，等.基于多因素模糊综合评价的某铁矿采空区危险度评定［J］.有色金属科学与工程，2011，2(4):71-75.ZHU Weimin，LI Xiang，CHEN Guoliang，et al.Risk assessment on an iron goaf based on multi-factor fuzzy comprehensive evaluation ［J］. Nonferrous Metals Science and Engineering，2011，2(4):71-75.

［5］张耀平，曹平，袁海平，等.复杂采空区稳定性数值模拟分析［J］.采矿与安全工程学报，2010，27(2):233-238.ZHANG Yaoping，CAO Ping，YUAN Haiping，et al.Numerical simulation on stability of complicated goaf［J］.Journal of Mining ＆ Safety Engineering，2010，27(2):233-238.

［6］张正兴，赵爱军，李威，等.基于空间分析的概率积分法在预测多煤层采空区塌陷中的应用——以青海塔妥煤矿为例［J］.中国地质灾害与防治学报，2012，23(4):94-98.ZHANG Zhengxing，ZHAO Aijun，LI Wei，et al.Application of probability-integral method base of spatial analysis for complex stratum layer:a case study of Tatuo coal mine［J］.The Chinese Journal of Geological Hazard and Control，2012，23(4):94-98.

［7］谢盛青.基于层次分析法采空区稳定性影响因素权重分析［J］.中国钼业，2009，33(4):34-37.XIE Shengqing.Weights analysis of factors that affect the stability of mined-out area on the foundation of ahp［J］.China Molybdenum Industry，2009，33(4):34-37.

［8］张庆庆，许月萍，牛少凤，等.变权欧式距离模型在水质综合评价中的应用［J］.中山大学学报(自然科学版)，2010，49(5):141-145.ZHANG Qingqing，XU Yueping，NIU Shaofeng，et al.Application of euclidean distance mode with varying weights in comprehensive assessmentof surface water quality ［J］.Journal of Sun Yat-sen University(Science and Technology)，2010，49(5):141-145.

［9］乔景顺.变权欧氏距离模型在边坡稳定性评价中的应用［J］.长江科学院院报，2013，30(7):81-85.QIAO Jingshun. Theeuclidean distancevariable weight model applied in the evaluation of slope stability［J］.Journal of Yangtze River Scientific Research Institute，2013，30(7):81-85.

［10］陈顺满，许梦国，王平，等.基于变权欧式距离的地下洞室岩体质量评价［J］.化工矿物与加工，2014(1):29-32.CHEN Shunman，XU Mengguo，WANG Ping，et al.Based on variable weight euclidean distance underground cavern rock mass quality evaluation［J］.Industrial Minerals＆ Processing，2014(1):29-32.

［11］王新民，柯愈贤，鄢德波，等.基于熵权法和物元分析的采空区危险性评价研究［J］.中国安全科学学报，2012，22(6):71-78.WANG Xinmin，KE Yuxian，YAN Debo，et al.Underground goaf risk evaluation based on entropy weight and matter element analysis［J］.China Safety Science Journal，2012，22(6):71-78.

［12］ZHOU J，LI X B，Mitri H S，et al.Identifcation of large-scale goaf instability in underground mine using particle swarm optimization and support vector machine［J］.International Journal of Mining Science and Technology，2013(05):701-707.

［13］刘文奇.均衡函数及其在变权综合中的应用［J］.系统工程理论与实践，1997(4):59-65.LIU Wenqi.Balanced function and its application for variable weight synthesizing ［J］. Systems Engineering-theory＆ Practice，1997(4):59-65.

［14］ZHANG H X，LU Y H，ZHANG J L.Euclidean distance harmonic method for establishing theoretical MAPK/Erk signaling pathway in treated breast cancer line MCF-7 ［J］.The Journal of China Universities of Posts and Telecommunications，2007(1):80-84.

［15］唐硕，罗周全，徐海.基于模糊物元的采空区稳定性评价研究［J］.中国安全科学学报，2012，22(7):24-30.TANG Shuo， LUO Zhouquan， XU Hai， etal.Evaluation of stability of goaf based on fuzzy matterelement theory ［J］.China Safety Science Journal，2012，22(7):24-30.

［16］刘华伟.基于可变权重理想点法的边坡稳定性评价［J］.水电能源科学，2014，32(5):101-104.LIU Huawei.Based on variable weighting ideal point method of slope stability evaluation ［J］.Water Resources and Power，2014，32(5):101-104.