卡尔曼滤波在精密机床装配过程误差状态估计中的应用

周强,刘志刚,洪军,郭俊康,刘鹏

(西安交通大学机械制造系统工程国家重点实验室, 710054, 西安)



卡尔曼滤波在精密机床装配过程误差状态估计中的应用

周强,刘志刚,洪军,郭俊康,刘鹏

(西安交通大学机械制造系统工程国家重点实验室, 710054, 西安)

针对精密机床装配偏差控制问题,在借鉴多工位装配中薄壁件装配偏差控制方法的基础上,建立了精密机床装配过程中偏差传递的状态空间模型,并提出了一种利用卡尔曼滤波实现对装配误差进行最优估计的新方法。首先,根据机床结构建立基准传递链,将零件关键特征在基础坐标系中位姿误差定义为状态变量,引入状态空间方程描述装配过程中的偏差传递,实现对装配工艺过程的数学表达。然后,基于状态空间模型,将当前装入零件加工误差作为系统输入误差,以当前装配步的测量结果为观测值,通过卡尔曼滤波计算装配误差最优估计值以及相应协方差矩阵,实现装配过程中装配误差的估计。最后,应用该方法对精密坐标镗床装配过程进行计算,结果表明:与传统公差分析计算方差相比,经过卡尔曼滤波计算得到最终装配状态估计误差的方差减小了63%,说明该方法用于评价装配过程中偏差累积是有效的,能为优化装配工艺和机床装配调整工艺提供有效指导。

卡尔曼滤波;机床装配;偏差传递;状态空间方程

为满足航空、汽车、轮船、能源等工业部门的高速发展,现代机床的加工精度已经显著提高。影响机床加工精度的因素主要包括:机床零部件在制造和装配时造成的空间误差、切削力引起的变形误差、热源引起的热变形误差、进给系统间隙与磨损造成的伺服跟随误差、数控系统的插补算法误差等[1]。与其他误差源相比,机床空间几何误差对加工精度的影响最大。精密机床空间几何误差主要是运动轴的运动误差和运动轴之间相对角度误差共同作用的结果。运动轴之间的角度误差是由于零件关键特征偏差在装配过程中传递和累积的结果。若能掌握装配过程中偏差传递规律,就能定量描述零部件精度对于整机精度的影响,实现对整机精度的预测与控制,从而有效指导装配过程调整工艺的实施。

近年来,很多学者对多工位装配中偏差传递、误差溯源及偏差控制等方面进行了详细的研究。文献[2]首次提出将机械装配分为两类:第1类是指产品装配精度由零件配合特征精度决定,如精密机床等机械设备的装配;第2类是指零部件的位置精度不以零件配合特征来定位,而是通过夹具定位来控制装配过程,并可在线调整改变偏差传递过程,例如飞机机身、汽车白车身等薄壁件的装配。文献[3]建立白车身装配过程中的状态空间模型,描述了夹具偏差与零件偏差对装配精度的影响。文献[4]对刚性零件装配的3类偏差源进行表达,并建立装机偏差传递及功能表达的装配偏差有向图模型。文献[5]以零件特征面为基本元素,研究零件偏差模型,建立第1类整机装配过程状态空间模型,但未对整机精度预测和偏差溯源进行深入研究。

本文针对精密机床装配过程偏差传递问题,在借鉴多工位装配中建模方法的基础上,建立了精密机床装配过程中偏差传递的状态空间模型,并提出一种利用卡尔曼滤波实现对装配几何误差状态进行最优预测的新方法。首先对机床的几何误差进行了分析和建模,分析零件偏差表达方法,然后建立机床装配过程中装配偏差流状态空间模型。运用卡尔曼滤波方法对装配过程中几何误差状态进行最优估计,获取当前状态下的装配精度。最后,以精密坐标镗床为实例,建立描述机床装配过程中关键几何特征变动,特征测量的状态空间模型。基于该模型,对装配过程进行分析与计算,结果表明,卡尔曼滤波最优预测能够准确预测装配偏差状态,可为评估机床装配工艺能力、优化装配工艺奠定基础。

1 机床装配过程状态空间建模

1.1 空间几何误差的形成

机床的支撑部件、进给系统、主轴系统、控制系统等在装配过程中装配成整体,达到最终的几何精度要求。机床常被看作是由床身、立柱、滑座、主轴、工作台组成的多体系统,因此可以采用多体系统理论进行研究。文献[6]基于多体系统理论和齐次坐标转换,提出一种针对数控机床几何误差建模、辨识、补偿的综合方法。文献[7]根据机床误差之间的因果关系将机床误差分为几何误差、运动误差、空间误差,后一层次的误差产生源于前一层次的误差,其中几何误差又分为导轨几何形状误差和配合几何误差导致的运动轴之间相对位置误差。3种误差的相互关系如图1所示。

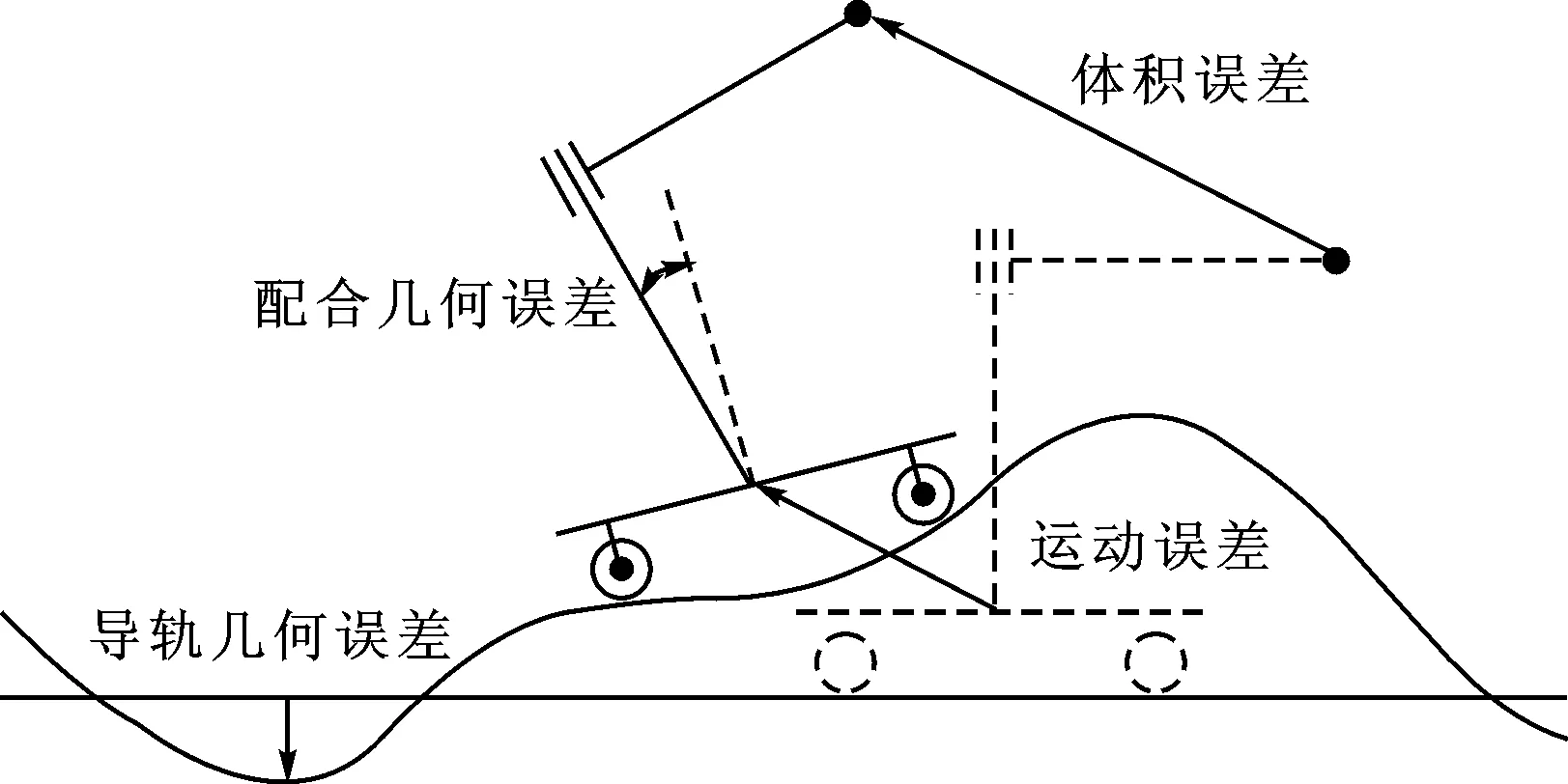
图1 几何误差、运动误差、空间误差的关系

空间误差是描述机床运动空间内刀具点与工件之间的位置与方位的总偏差。空间误差是由单轴运动误差与运动轴之间的几何位置误差共同作用的结果。其中,机床单轴运动误差主要受导轨制造精度的影响,并且可以通过装配完成后数控系统进行补偿。运动轴之间的配合几何误差主要是由机床零部件配合特征面的加工误差以及装配过程中偏差累积误差引起的。运动轴之间相对位置误差在整机装配完成后形成固定系统误差,影响机床精度性能的提升。因此,有必要研究机床装配过程中偏差传递规律,建立装配过程偏差传递的数学模型,预测并控制装配偏差,从而提高机床装配精度。

1.2 机床装配过程状态空间方程

在精密机床装配过程中,零部件关键配合特征偏差以及装配过程中的偏差传递与累积影响机床整机精度的提高。因此,本文首先将零件偏差进行数学表达;其次引入状态空间模型,将机床的关键几何特征误差状态作为状态变量,以实际测量数据作为观测量,定量描述零部件精度对机床整机精度的影响,实现对机床装配过程中偏差积累的数学建模。

1.2.1 零部件偏差的描述 机床装配误差模型是:基于零件特征描述零件之间配合特征相对位置、方位等装配的约束关系。零部件是机床装配中的基本单元,为描述机床装配过程中的偏差传递规律,首先需要对零件特征的偏差进行表达。如图2所示,o0-x0y0z0为零件坐标系,o1-x1y1z1为零件理想特征坐标系,o2-x2y2z2为实际特征坐标系。特征坐标系位于关键几何特征中心处,表征关键特征的位置与方位。

图2 零件关键特征加工偏差

由于加工制造误差,实际加工的特征面表面与理想特征面存在位置与方位误差。Δx、Δy、Δz表示实际特征坐标系与理想坐标系之间位置误差,Δθx、Δθy、Δθz表示实际特征坐标系相对于理想坐标系的方位误差。根据新一代GPS标准,对实际几何特征表面进行测量,对特征表面进行数据提取、分离、拟合得到实际特征表面。根据设计公差要求、理想特征面可以确定实际特征面的偏差值大小。因此,零件实际特征面的偏差可以表示为

(1)

1.2.2 状态空间方程 建立精密机床装配过程中状态空间方程,关键在于确定状态变量以及状态方程和输出方程中的系数。首先定义状态变量X(k)表示第k个零件装配完成后,基准信息链中配合特征坐标系的位置和方位相对于理想位置和方位的偏差[8]

(2)

式中:dk为微分平移矢量;δk为微分旋转矢量。

假设X(k+1)定义为描述第k个零件装配后特征面相对于基准信息链中基础坐标系的总累积偏差,w(k)表示装入的第k个零件在零件坐标系中的偏差,那么第k个零件装配过程的状态方程可表达为

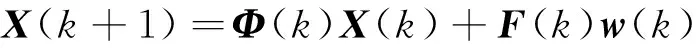
(3)

式中:Φ(k)为单位矩阵;F(k)为将零件偏差从零件坐标系转化到基础坐标系的转换矩阵。机床装配过程如图3所示。

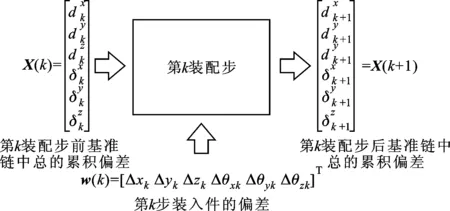
图3 机床装配过程状态空间模型

式(3)实现了将三维空间中的偏差传递等价于基准信息传递链中坐标转换中的误差传递。借鉴机器人领域精度预测的方法[2],利用齐次坐标转换表达零件坐标系之间相对位置关系,通过坐标系之间的转换来预测单个零件偏差对整机最终位置和方位的影响。因此,第k个零件装配完成后相对于基础坐标系的微分平移矢量dk和微分旋转矢量δk可以写成

(4)

(5)

根据文献[9-10],将式(4)、式(5)展开为

(6)

从式(6)可以看出,装入第k个零件后,第k个零件的偏差与k-1状态下累积偏差共同引起的总累积偏差、平移和旋转误差影响最终的装配位置误差,而最终的位姿误差只与旋转误差相关。本文重点关注关键特征的相对位姿误差对于最终装配精度的影响,只考虑角度偏差,简化式(6),可以得到

(7)

对比式(3)和式(6),可以得到状态方程中的参数Φ(k)、F(k),机床装配过程的状态变量简化为

装配过程需要了解关键几何特征误差状态,判断是否满足设计装配精度要求,指导后续的装配工艺的实施。因此,定义Z(k)为装配体几何特征中的关键特征的测量量,则装配过程中的观测方程为

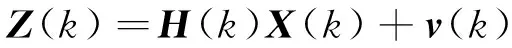
(8)

式中:H(k)为r×3元素为0或1的观测矩阵,定义为零件上关注的几何特征;Z(k)为输出矢量;v(k)为测量过程中的测量白噪声。

根据上面的讨论,将考虑零件偏差及测量工艺的机床装配过程视为线性离散事件过程,系统的状态定义为误差状态变量,其状态空间方程为

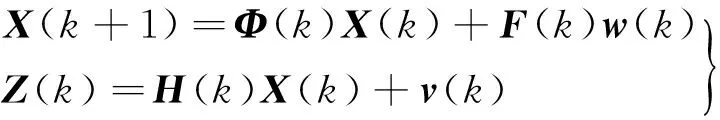
(9)

在机床装配过程中,状态空间模型为描述零件或者子装配体装入到多工位装配过程中旋转角度累积误差的产生、传递提供了可能。相比于传统几何误差模型,状态空间模型中考虑了测量环节,因此具有更高的精度。

2 卡尔曼滤波误差状态最优估计

在实际装配中,由于机床结构和测量方法的限制,有些关键特征几何误差不能直接获得,需要通过测量工具对其他相关特征进行测量,根据测量得到的数据来确定装配误差状态。因此,引入现代控制工程中广泛应用的卡尔曼滤波方法,解决装配过程中的装配误差状态估计问题。

假设机床装配过程的几何误差状态服从均值为0、协方差矩阵已知的高斯分布。w(k)是第k个零件带入装配中的偏差,定义为零件上两个关键特征的相对角度误差。将零件误差视为设计与制造过程满足设计公差要求的统计分布,因此零件偏差定义均值为0、方差为设计公差Qk的随机变量序列,满足

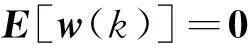
(10)

式中:Qk为非负正定矩阵,表征零件的设计公差要求;δkj为克罗尼克函数。

假设ν(k)为测量过程中的测量噪声,当满足期望为0、方差取决于测量装置与测量方法的精度,并且零件加工误差和测量噪声相互独立时,满足

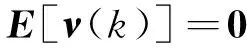
(11)

式中:Rk为正定矩阵,表征测量方法的不确定度。

卡尔曼滤波理论上主要包括滤波问题、预测问题和平滑问题。本文应用卡尔曼滤波预测方法,推导预测递推方程如下[11]

(12)

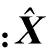
卡尔曼滤波的优势在于能够根据最新测量值修正前装配步的偏差估计值,能够实时更新系统的状态,其递推过程如图4所示。

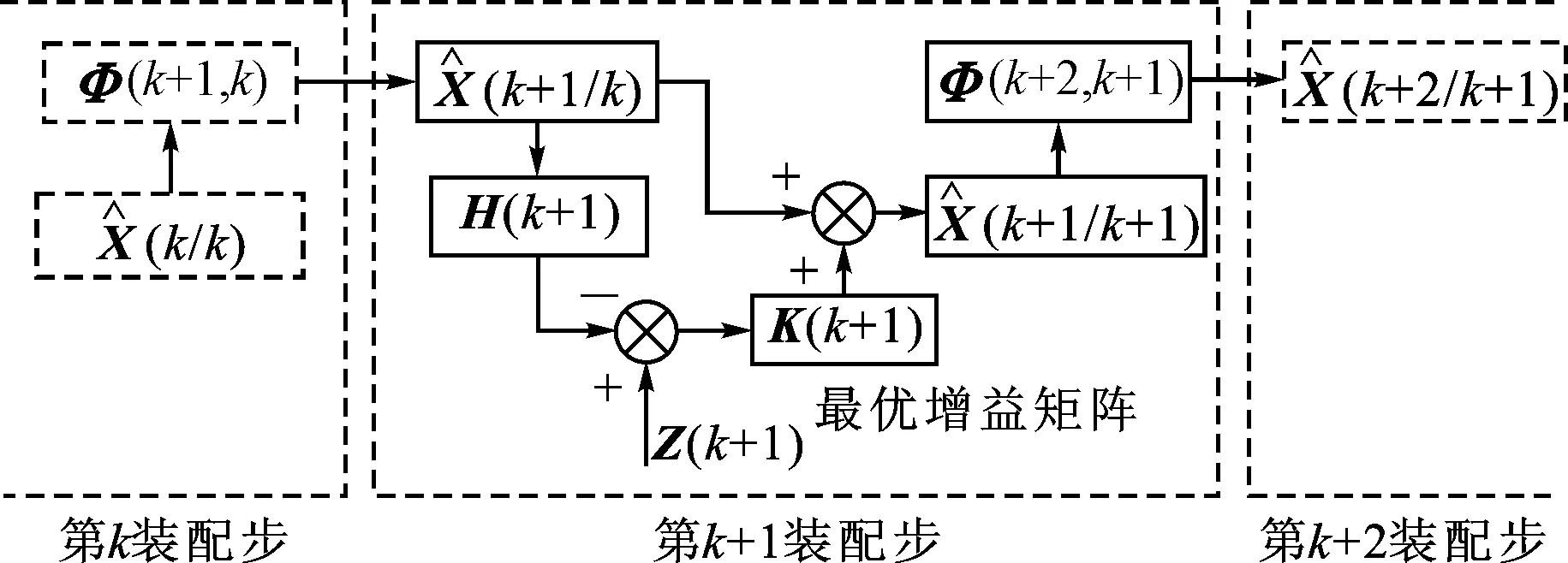
图4 卡尔曼滤波递推公式

在机床装配过程中,最优滤波模型能够估计几何特征角度误差的大小,通过当前装配步中观测值与上一步装配中最优估计量比较,对当前状态进行修正并能对实际的偏差状态进行最优估计。从滤波方程中可以得出P(k+1/k+1)只与Rk、Qk相关,而与测量量的大小无关。因此,为提高最优估计精度,可以减小装配零件几何误差的不确定度或减小测量工艺的不确定度。在实际装配中可提高零件设计公差或采用精度更高的测量工具。

根据精密机床装配过程的状态空间方程,将当前零件加工误差作为系统输入误差,以当前装配步的测量结果为观测值,通过卡尔曼滤波线性递推公式,能够预测出当前装配误差最优预测值,并计算出相应协方差矩阵,实现对装配过程装配角度误差的估计,为装配工艺评估、装配偏差控制提供依据。

3 实例分析

以某型号精密坐标镗床为例,按照本文所述建模方法,对机床床身(A)、立柱(B)、滑座(C)、主轴箱(D)、工作台(E)等5个零部件机床装配过程进行建模,运用本文提出的状态空间方程方法和误差状态最优估计对装配误差进行分析。图5所示为坐标镗床结构及基准传递链。

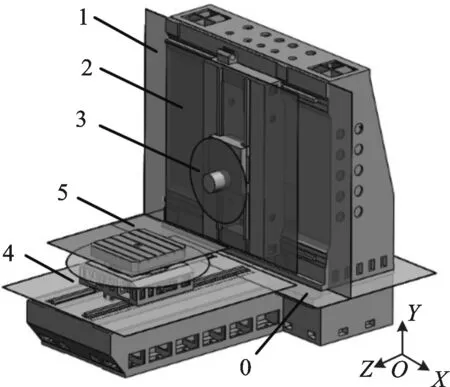
(a)精密坐标镗床结构

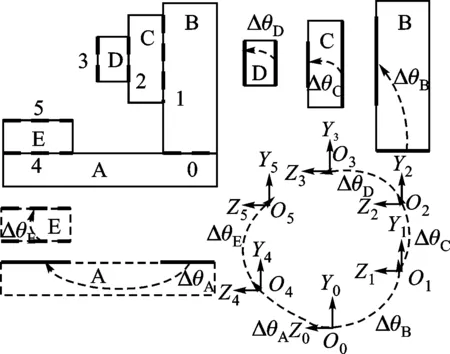
(b)基准传递链图5 坐标镗床基准传递链

由前文分析可知,精密坐标镗床的几何精度主要受关键几何特征之间的相对角度误差影响。因此,选取机床工作台面、Z轴与床身安装面、床身立柱结合面、X轴与立柱安装面、Y轴与滑座安装面、主轴箱基准面等6个关键几何特征面作为研究对象,研究装配过程特征面之间的角度误差的累积与传递过程。在空间坐标系中,关键特征面又分别绕X、Y、Z轴旋转,且绕3个轴的旋转自由度相互独立互不影响,因此X、Y、Z轴旋转偏差累积过程相互独立。为简化建模过程,以下只考虑特征面绕X轴旋转,即只计算YZ平面内的偏差传递过程。

3.1 偏差传递建模

在机床装配过程中输入几何误差为零件上关键特征之间的角度误差,这个误差主要由加工过程产生,因此输入误差的标准差可以通过设计公差给定。基础部件的设计公差由表1给出。

表1 基础大件关键特征面设计公差

将床身与立柱之间的结合面作为基础坐标系,根据式(6),整机装配完成后,在YZ平面内最终误差状态方程可表示为

(13)

第k+1步装配误差状态由第k步装配误差状态与第k步输入的零件误差共同决定,因此整机装配过程中的状态空间方程可改为

(14)

对于精密坐标镗床基准传递链,坐标系间理想转换没有角度变化,因此根据式(9),可确定卡尔曼滤波方程中的各项系数矩阵为

A(k+1,k)=I

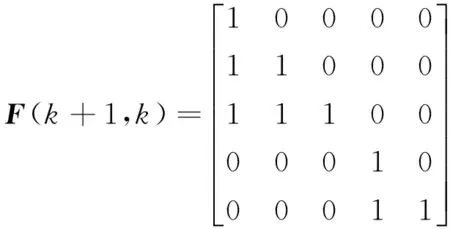
根据精密坐标镗床实际装配过程中的装配工艺,确定基础部件的装配顺序、输入误差的协方差矩阵,以及装配步中关键几何特征对之间的平行度或者垂直度误差的测量工艺,详细数据见表2。

观测矩阵H(k)为1×5的行向量,用于表征所测量的特征面误差的变化。测量不确定度表示用某种测量仪器对观测特征测量值的不准确程度,下节以测量床身装配过程为例说明不确定度的评价过程。

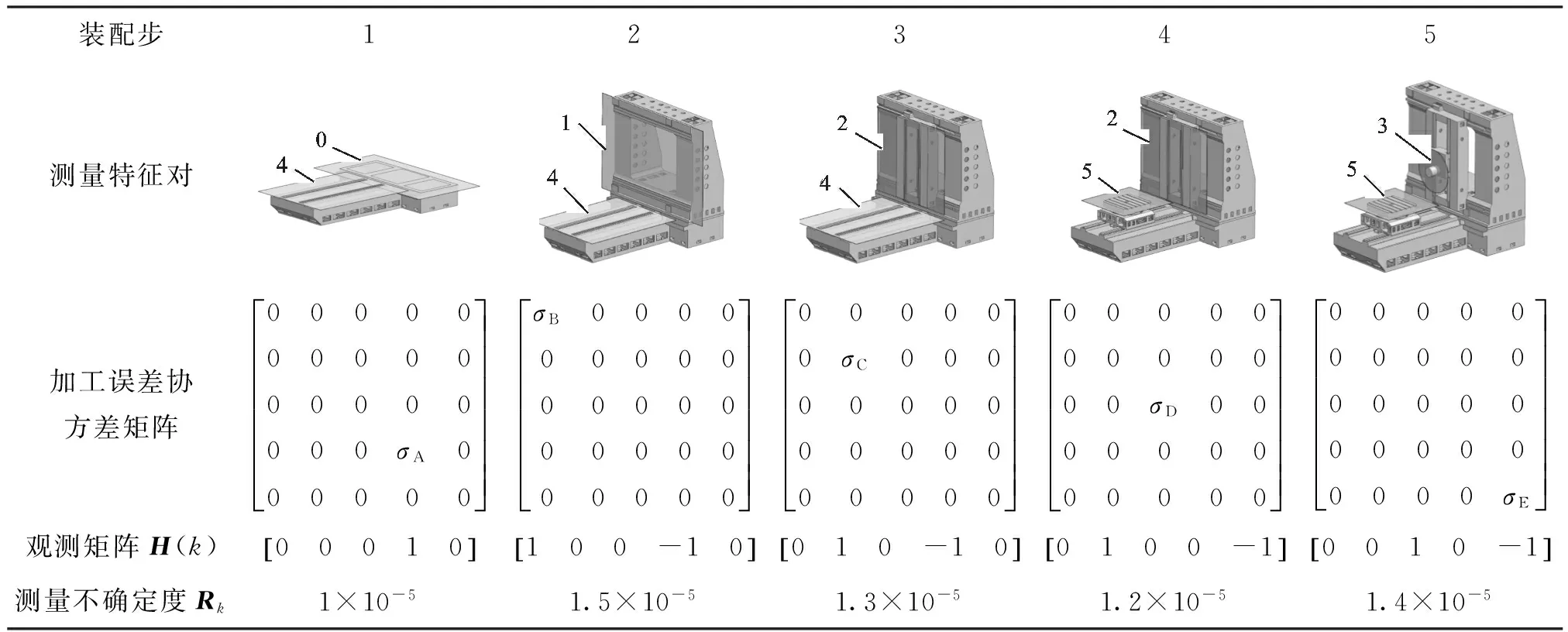
表2 机床装配过程的装配工艺数据

注:σA、σB、σC、σD、σE分别为机床基础大件床身、立柱、滑座、主轴箱、工作台的特征面角度偏差的标准差。

3.2 测量工艺不确定度评定

床身装配过程中主要关注床身立柱结合面与Z轴安装平面的平行度误差。首先调整床身水平,使用电子水平仪先测量其中一个面,然后以这个测量面为基准测量另一平面,获得测量数据。采用常用的最小二乘法对两平面的平行度误差进行计算。

根据平面度最小二乘拟合的规则,要求每个提取点到理想平面距离的平方和最小。因此,假定最小二乘平面为z=ax+by+c,a、b、c为估计参数。假设取样点中位于最小二乘拟合平面两侧最大偏离点为(x1,y1,z1)、(x2,y2,z2),因此平行度最小二乘法评价模型为

在两平面的平行度测量过程中不确定来源主要有:水平仪重复性测量引起的不确定度分量以及水平仪示值误差引入的不确定度分量。确定测量重复性不确定度是通过在测量范围取点进行重复性试验,每点重复测量10次,根据贝赛尔法确定各点的标准差,取其中最大值作为水平仪重复性测量引起的不确定度。水平仪的示值误差为±1.2 μm,服从均匀分布,u2=1.2/31/2=0.693 μm。

根据不确定度模型确定的传递系数、单点测量不确定度以及合成不确定计算公式,可以得到电子水平仪测量床身平行度的不确定度uc≈1 μm。

3.3 计算结果

根据表2中初始条件以及式(11)进行计算分析,得到装配过程中关键几何特征在各个装配步中的状态误差值以及估计误差的方差。

传统公差分析方法计算的结果如图6所示,其中p1、p2、p3、p4、p5是预测误差协方差矩阵P(k)的对角元素。通过与传统公差分析方法得到的结果对比可以看出,由卡尔曼滤波最优估计方法计算的估计误差显著减小,说明本方法用于评价装配过程中偏差累积是有效的,并能够为后续优化装配工艺和机床装配调整工艺提供有效指导。

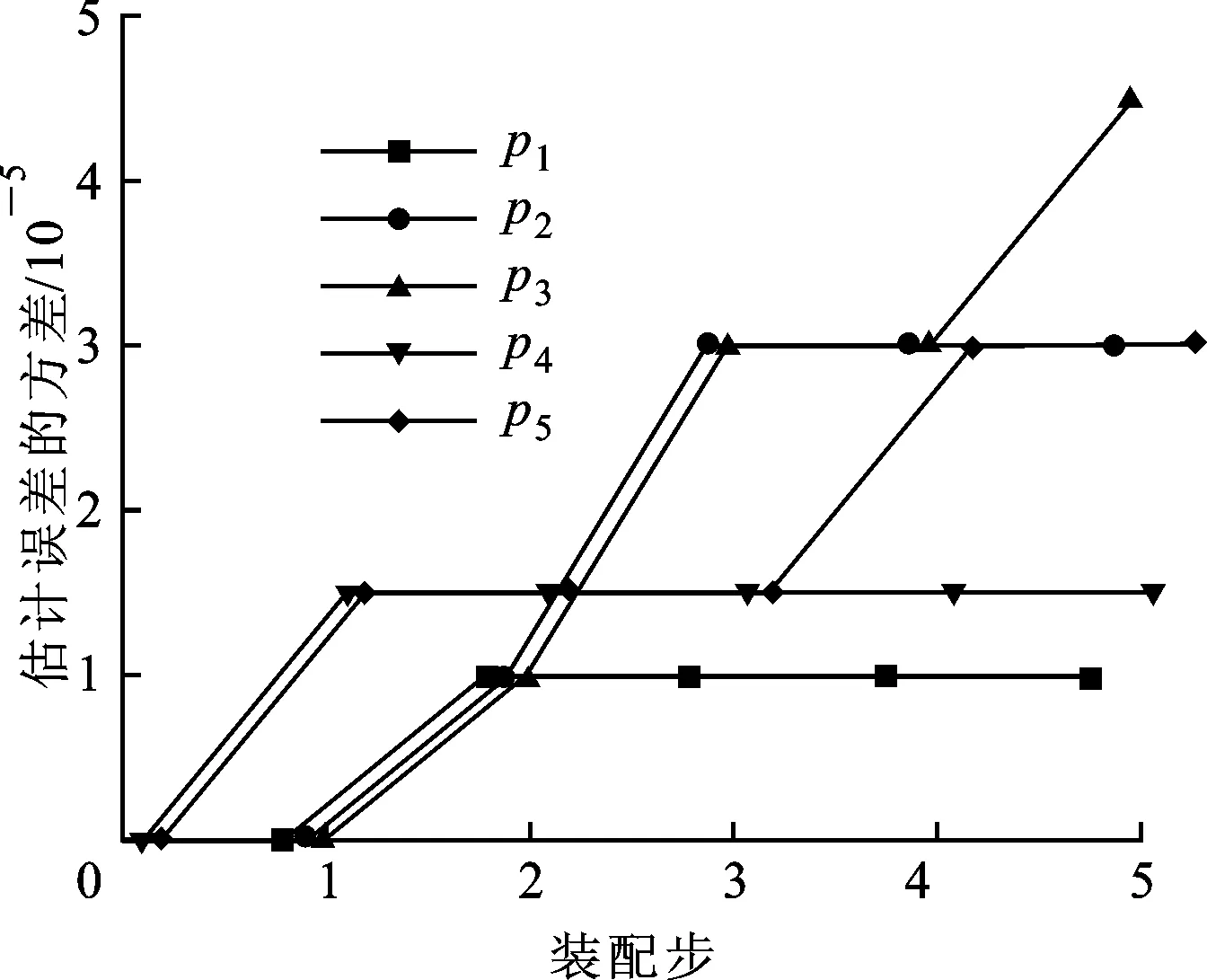
图6 传统公差分析方法

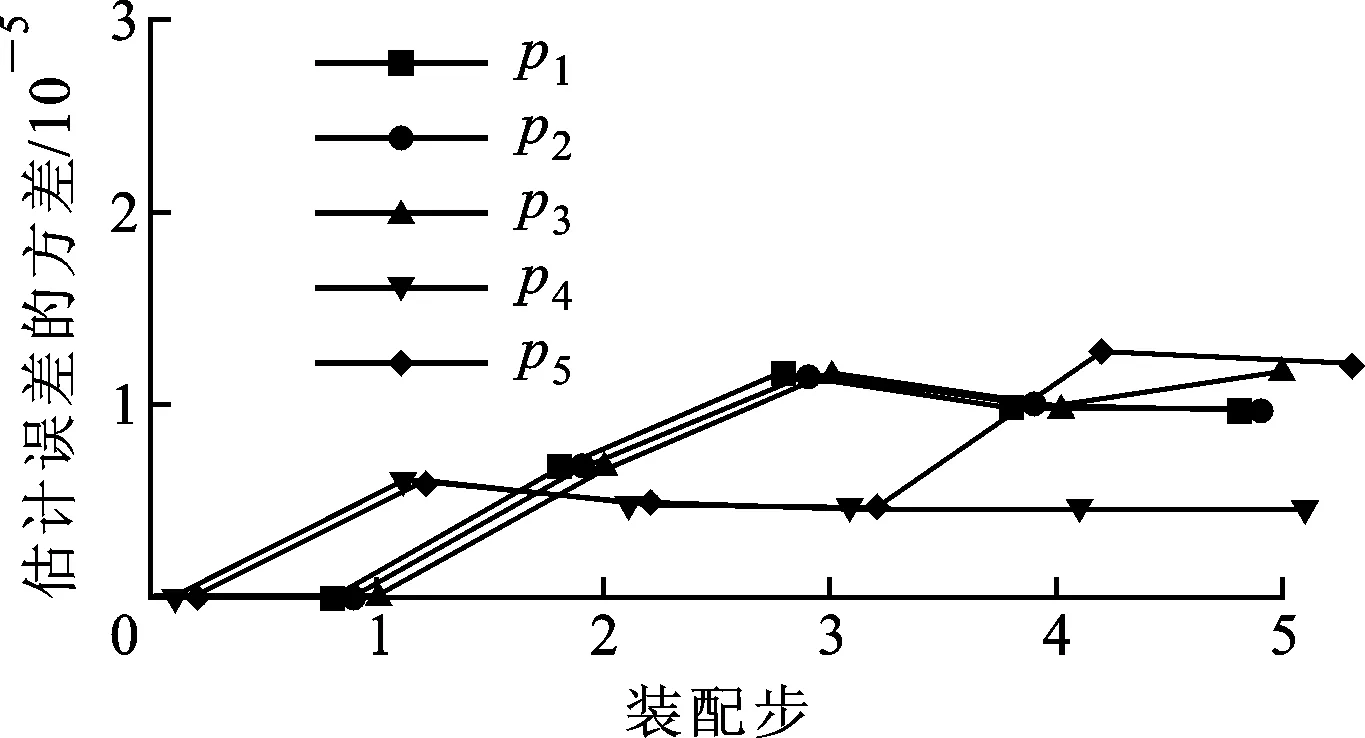
图7 卡尔曼滤波最优估计

本实例中应用状态空间方程对某型号精密坐标镗床装配过程进行了建模,运用卡尔曼滤波对装配偏差状态进行了最优预测。该方法构建了机床装配过程的装配工艺与测量工艺的数学模型,为预测最终装配精度、评价装配工艺以及装配阶段的调整工艺奠定了理论基础。

4 总 结

(1)根据机床基准信息链,以机床装配过程装配偏差为状态变量,建立考虑零件偏差与测量工艺的装配过程状态空间模型,将装配过程转化为线性离散系统进行研究。

(2)利用卡尔曼滤波实现对状态空间模型中几何误差状态进行最优预测,与传统公差计算方法相比精度更高,更具实际应用意义,同时考虑装配顺序、测量工艺的最优估计算法,为机床设计人员提供了一种工艺规划的新评价方法。

(3)通过坐标镗床装配过程的实例仿真分析,及与传统公差分析的结果对比,验证了基于卡尔曼滤波的精密机床装配精度预测方法的有效性。

[1] 粟时平. 多轴数控机床精度建模与误差补偿方法研究 [D]. 长沙: 国防科学技术大学, 2002.

[2] MANTRIPRAGADA R, WHITNEY D E. Modeling and controlling variation propagation in mechanical assemblies using state transition model [J]. IEEE Transactions on Robotics and Automation, 1999, 15(1): 124-140.

[3] 田兆青, 来新民, 林忠钦. 多工位薄板装配偏差流传递的状态空间模型 [J]. 机械工程学报, 2007, 43(2): 202-209. TIAN Zhaoqing, LAI Xinmin, LIN Zhongqin. State space model of variations stream propagation in multistation assembly processes of sheet metal [J]. Chinese Journal of Mechanical Engineering, 2007, 43(2): 202-209.

[4] 刘伟东, 宁汝新, 刘检华. 机械装配偏差源及其偏差

传递机理分析 [J]. 机械工程学报, 2012, 48(1): 156-168. LIU Weidong, NING Ruxin, LIU Jianhua. Mechanism analysis of deviation sourcing and propagation for mechanical assembly [J]. Chinese Journal of Mechanical Engineering, 2012, 48(1): 156-168.

[5] 何博侠, 张志胜, 戴敏. 机械装配过程的偏差传递建模理论 [J]. 机械工程学报, 2008, 44(12): 62-68. HE Boxia, ZHANG Zhisheng, DAI Min. Theory of modeling variation propagation of mechanical assembly processes [J]. Chinese Journal of Mechanical Engineering, 2008, 44(12): 62-68.

[6] 粟时平, 李圣怡, 王贵林. 多轴数控机床的通用运动学综合空间误差模型 [J]. 国防科技大学学报, 2001, 23(4): 45-50. SU Shiping, LI Shengyi, WANG Guilin. A universal synthetic volumetric error model of multi-axis NC machine tool based on kinematics [J]. Journal of National University of Defense Technology, 2001, 23(4): 45-50.

[7] EKINCI T O, MAYER J R R. Relationships between straightness and angular kinematic errors in machines [J]. International Journal of Machine Tools and Manufacture, 2007, 47(12/13): 1997-2004.

[8] 洪军, 郭俊康, 刘志刚. 基于状态空间模型的精密机床装配精度预测与调整工艺 [J]. 机械工程学报, 2013, 49(6): 114-121. HONG Jun, GUO Junkang, LIU Zhigang. Assembly accuracy prediction and adjustment process modeling of precision machine tool based on state space model [J]. Chinese Journal of Mechanical Engineering, 2013, 49(6): 114-121.

[9] GUO Junkang, HONG Jun, WU Xiaopan, et al. The modeling and prediction of gravity deformation in precision machine tool assembly [C]∥ASME 2013 International Mechanical Engineering Congress and Exposition. San Diego, CA, USA: ASME, 2013: V02AT02A087.

[10]WHITNEY D E, GILBERT O L, JASTRZEBSKI M. Representation of geometric variation using matrix transforms for statistical tolerance analysis in assembly [J]. Research in Engineering Design: Theory Applications and Concurrent Engineering, 1994, 6(4): 191-210.

[11]周凤岐, 卢晓东. 最优估计理论 [M]. 北京: 高等教育出版社, 2009: 23-67.

(编辑 杜秀杰)

Kalman Filter with Applications to Assembly Accuracy State Estimation for Precision Machine Tool

ZHOU Qiang,LIU Zhigang,HONG Jun,GUO Junkang,LIU Peng

(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710054, China)

In terms of variation control strategy for sheet components assembly, a state space model (SSM) of variation propagation for precision machine tools in assembly process is established and a new method for optimally estimating assembling error by Kalman filter is proposed. Datum flow chain (DFC) of the machine is set up according to the machine topology, and the position and orientation error of key character of the part in DFC is defined as state variable. The SSM is introduced to describe the variation propagation and accumulation of assembly process to acquire the mathematical expression. The optimal estimation and corresponding covariance matrix of assembly error can be calculated by Kalman filter method, which synthesizes the measuring results of current assembly step. The suggested approach is applied to the assembly process in a precision machining center. The results show that the variances of estimation errors at final assembly step are reduced significantly by 63% using Kalman filter method compared with ones from the traditional tolerance analysis.

Kalman filter; machine tool assembly; variation propagation; state space model

2015-05-18。

周强(1990—),男,硕士生;刘志刚(通信作者),男,教授。

国家高技术研究发展计划资助项目(2012AA040701)。

时间:2015-09-13

10.7652/xjtuxb201512016

TH161

A

0253-987X(2015)12-0097-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150913.1827.010.html