组合模型EPS转矩转角传感器可靠性预测

马峻

（北京电子科技职业学院汽车工程学院，北京 100026）

组合模型EPS转矩转角传感器可靠性预测

马峻

（北京电子科技职业学院汽车工程学院，北京 100026）

为提高电动助力转向系统的性能，设计一种电动助力转向系统转矩转角传感器，并建立数学模型对传感器的可靠性进行预测。在实验的基础上比较灰色GM（1，1）模型、残差修正的灰色GM（1，1）模型以及残差修正的灰色马氏链组合模型的预测准确度。由于单个模型很难保证预测准确度水平，因此通过计算组合模型不同步数的转移概率矩阵确定目标状态，进而得到预测值。通过比较，组合模型比单个模型的准确度更好，更适宜描述随机性较大的问题。

转矩转角传感器；灰色GM（1，1）模型；残差修正；马氏链

0　引　言

随着汽车技术的发展，驾驶者为追求驾乘的乐趣，对转向系提出了更高的要求。由于电动助力转向系统（EPS）较好地解决了“轻”与“灵”的统一，得到迅猛发展。EPS不仅可以提高汽车在高速下的操纵稳定性，还能减小转向系统的质量并节省能源，根据汽车车型的不同，使用电动助力系统能够减少3%～5%的燃油费用[1]。EPS在结构上实现了环保化、轻量化，符合未来汽车发展的方向，特别是对于环保型电动车而言，EPS具有更明显的优势。据统计，我国2007年至2012年间，EPS消费量呈爆发式增长，由2007年的62万套增至2012年的600万套[2]；但这一数字对于我国2.53亿辆的汽车保有量来说，所占比例仍不算太高。随着我国汽车产业的发展，EPS消费量将继续增加，据世界著名的咨询公司Strategy Analytics对全球转向系统的预测，到2015年中国将超过欧美和日本，成为全球最大的EPS市场。

EPS通过传感器，测得扭矩、转角、车速等信号，并据此分配转向助力矩。因此，传感器可以看做EPS的“眼睛”，“视力”的好坏直接决定了整套系统的工作性能。随着汽车电子技术的发展，为了更精确的分配转向助力矩，仅获得转矩信号已经不够，转角信号的采集同样重要。目前国产EPS采用分别安装转矩、转角传感器来获取相关信号，但这样的系统结构复杂，稳定性差，且分别安装的传感器均占用一定空间。因此，设计高准确度、低成本、具有自主知识产权的转矩转角集成传感器是发展国产EPS重要的内容之一。

1　转矩转角传感器的设计

目前的转矩传感器芯片主要有电位计式、光电式、电感式及磁阻式等[3-7]，本文选用英飞凌公司推出的基于巨磁电阻原理的TLE5011角度传感器作为传感器的芯片，它能够较好地满足车用传感器的使用条件。

传感器齿轮结构设计如图1所示，设大齿轮1齿数为Z1、大齿轮2齿数为Z2；双联齿轮3，4，5中小齿轮齿数分别为Z3′、Z4′、Z5′，大齿轮齿数分别为Z3、Z4、Z5；小齿轮6，7，8齿数分别为Z6、Z7、Z8；经计算，选取Z1=Z2=84；Z3′=Z4′=Z5′=15；Z3=Z4=Z5=45；Z6=Z7=35；Z8=36。为消除齿轮机构的回差，提高测量准确度，将齿轮的变位系数设计成线性函数，通过变位系数由0.08到-0.08的变化使齿轮在齿宽方向上形成约3°的锥角，通过这样的结构消除齿轮传动的回差，提高准确度，小锥角的齿轮外形还便于注塑生产[8]。

2　转矩转角传感器可靠性预测

图1　传感器齿轮组布置

车用传感器的可靠性一般以真实产品的破坏性试验来标定。试验中将样品放在模拟或真实的工作环境下测量其在一定工作循环次数后的失效状态，并利用次序统计量理论来进行可靠性特征的最后确定，统计失效率、平均可靠性指标。但转矩转角传感器工作时负载较小，同时随着电子科技的发展，当前电子元器件及材料的可靠性均有大幅度提高。这样的前提下，进行破坏性试验的时间与金钱成本均比较高。为了得到更准确、合理的可靠性指标，可以采用数学模型的方法进行预测[9]。但单个模型预测往往存在一定缺陷，如灰色预测模型对于离散变量的预测准确度无法较好控制，且一般只用于小样本数据，当数据较多，离散程度较大时，其预测准确度较差[10]；时间序列分析模型建模过程复杂，且只善于分析大样本数据[11]；马尔科夫过程偏重无后效性数据序列的预测[12-13]；指数回归模型则要求大量的样本且具有较好的分布规律[14]。近年来，通过将不同模型预测方法进行优化组合产生新的组合模型进行预测的方法发展迅速[15-18]，这为转矩转角传感器的可靠性预测提供了新的思路。

2.1转矩转角传感器可靠性预测模型的建立

对转矩转角传感器齿轮组取20件样品进行加载的可靠性试验，指定失效个数为10的无替换定数截尾实验，实测齿轮寿命按时间长短排序，如表1所示。

表1　齿轮寿命试验数据

选取1～5号数据为基础，进行灰色系统建模。

2.2灰色系统GM（1袁1）建模与预测

以1～5号数据为基础，建立原始数列x（0）：

其中：

对生成的序列x（1）建立GM（1，1）模型微分方程，即：

根据z（1）和x（0）可列出：

则微分方程为

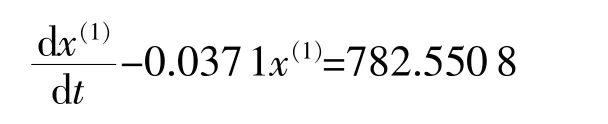
方程的解为

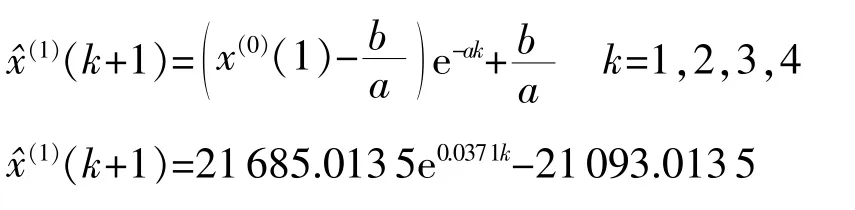
将其还原成GM（1，1）模型的预测值：

由式（1）求得的预测数据与实际数据的对比如表2所示，根据GM（1，1）模型得出的预测值求出预测值与实际值之间的残差ε（0）（k）=x（0）（k）-（0）（k），进而求出残差相对值

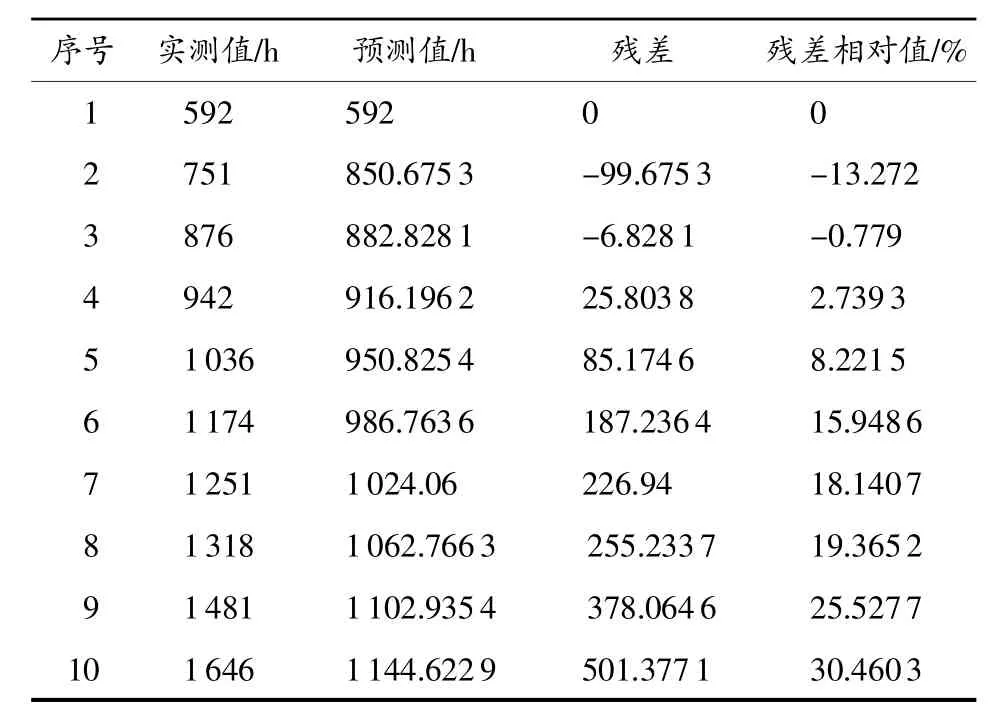
表2　GM（1袁1）灰色模型预测结果及残差分析

2.3灰色GM（1袁1）模型的残差修正

由表2分析数据可以看到，6～9号数据的残差较大，预测准确度较低，为提高预测准确度，应采用残差修正的办法，对数据的残差再次建立GM（1，1）模型，用残差的GM（1，1）预测值与原来的预测值相加，来弥补原预测值的不足，达到提高准确度的目的[19]。根据表2中的数据，取i0=6，得到残差序列：

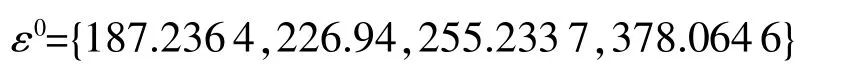
对ε0进行一次累加（1-AGO）生成：

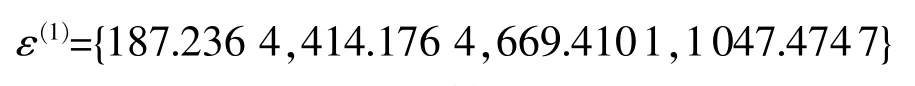
ε（1）的紧邻值生成序列为

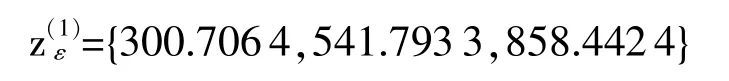
建立GM（1，1）模型微分方程，即：

由式（3）得到的预测值、残差、残差相对值如表3所示。

表3　残差修正 GM（1袁1）模型预测结果尧残差分析及状态划分

2.4马氏链模型的建模与预测

马氏链即马尔科夫过程，于1906年由前苏联数学家A.A.Markov提出，经过一百多年的演变，在理论上已十分完善，是随机过程领域的重要组成，对于无后效性数据序列的预测准确度较高。

将表3中的残差相对值划分为3个状态，σ1=（-15，-5]，σ2=（-5，0]，σ3=（0，10]，相对值所对应的状态如表所示，建立马氏链模型。

转移1步所对应的概率矩阵：

转移2步所对应的概率矩阵：

转移3步所对应的概率矩阵：

转移4步所对应的概率矩阵：

转移5步所对应的概率矩阵：

选取残差修正模型样本5～9号，转移步数分别为5，4，3，2，1。转移步数所对应的转移矩阵中，取起始状态所对应的行向量，组成新的概率矩阵，如表4所示。

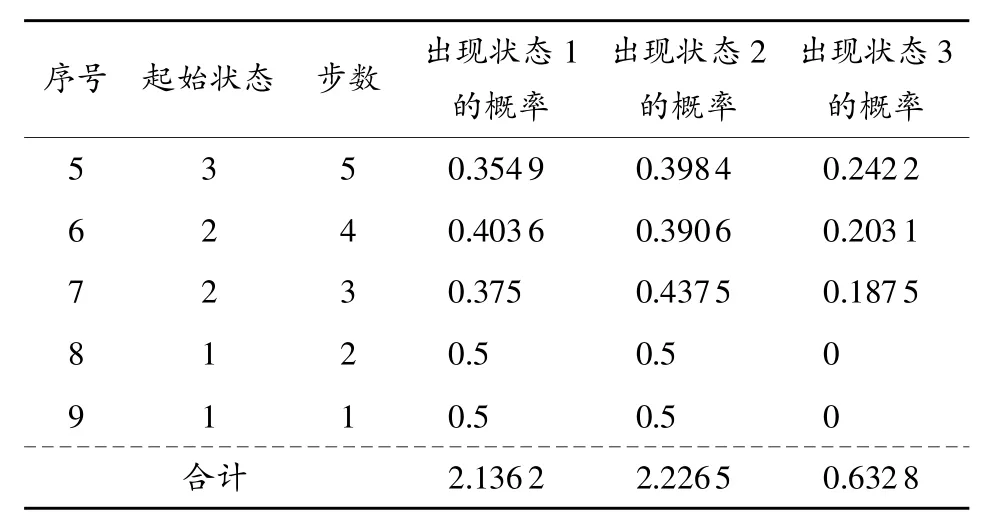
表4　10号样本马氏链状态转移矩阵

由表可知，10号样本在状态2的概率合计为2.226 5，其值最大。因此，预测10号样本处于状态2，由前文状态划分可知σ2=（-5，0]，同时由表3可知，10号样本基于残差修正GM（1，1）模型预测值为1779.3199h。

因此，基于残差修正灰色马氏链模型的预测值为

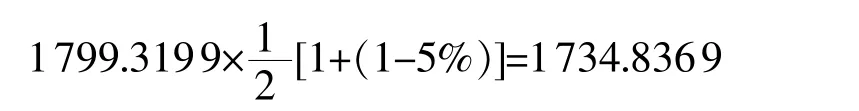
比较10号数据的预测结果可知，单独使用GM（1，1）模型预测，其残差相对值为30.46%，使用残差修正后，其残差相对值为-8.1%，使用灰色马氏链组合模型预测，其残差相对值-5.4%。

实测数据与3种预测结果的比较如图2所示，残差修正后的灰色马氏链组合模型预测与实验结果基本相符，使用该模型预测比单独使用灰色GM（1，1）模型和残差修正的灰色GM（1，1）模型预测准确性上有所提高。

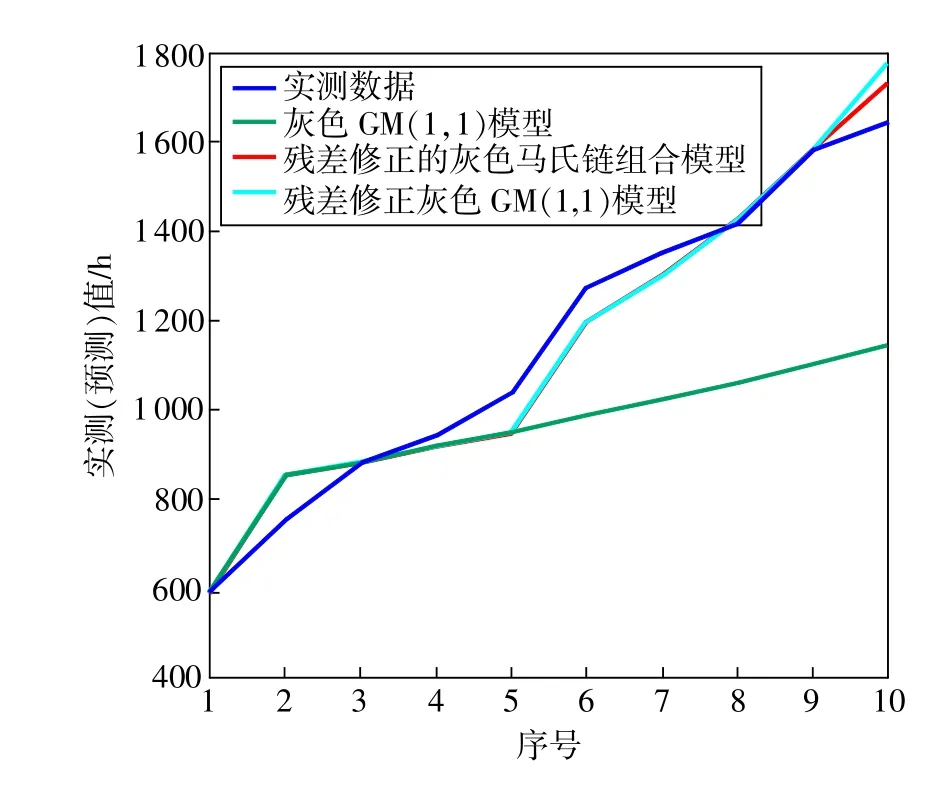
图2　预测结果比较

3　结束语

1）灰色GM（1，1）模型具有一定缺陷，对于受外界因素影响较大的传感器可靠性预测准确度较差。

2）残差修正后的灰色GM（1，1）模型可以提高一定的准确度。

3）使用残差修正的灰色马氏链组合模型能够得到比较高的模型预测准确度，这种组合模型更适合描述随机性较大的预测问题。

4）使用无替换定数截尾实验，可以将试验时间由1646h降低到数据处理后的1481h，节约了试验时间和经费，同时采用相对较少的数据建模可以减少失效样品数，节约了成本。

5）对组合模型的状态划分、转移步数等的不同取值会影响预测的结果和准确度，要进行反复的比较才能得到最高的准确度。

[1]Environmentally FriendlyProducts.ElectronicPower Steering[J].Motion&Control NSK，2002（12）：23-27.

[2]智研咨询集团.2014～2019年中国汽车EPS产业竞争格局与未来发展趋势报告[R].北京：智研咨询集团，2014.

[3]Akira N.Development of a Steering Angle and Torque Sensorof Contact-type[J].Furukawa Review，2004（25）：36-41.

[4]Yuji K.Electric Power Steering（EPS）[J].Motion&Control NSK，1999（6）：9-15.

[5]Osuka A.Development of pinion-assist type electric power steering system[J].KOYO Engineering Journal Edition，2002，（16）：46-51.

[6]Hazelden R J.Optical torque sensor for automotive steering systems[J].Sensors and Actuators，1993（37/38）：193-197.

[7]季学武.电动助力转向系统光电式转矩传感器的研究[J].仪表技术与传感器，2004，34（4）：65-67.

[8]马峻，刘本林.车用转矩转角传感器无侧隙齿轮系统设计[J].仪表技术与传感器，2014（4）：77-79.

[9]谢常青，赵延明.车用电子设备电子器件寿命组合预测[J].测试技术学报，2008（3）：189-193.

[10]刘思峰，郭天榜，党耀国.灰色理论及应用[M].北京：科学出版社，1999：44-60.

[11]佘娣.基于灰色与时序的组合模型在变形监测中的应用研究[D].桂林：桂林理工大学，2012.

[12]Wu K，Lin Z H.Application of markov chain in VLSI power estimation［J］.Computer Engineering，2003，29（13）：162-164.

[13]A T巴鲁查·赖特.马尔科夫过程论初步及其应用[M].上海：上海科学技术出版社，1979：82-90.

[14]陈玉祥，张汉亚.预测技术与应用[M].北京：机械工业出版社，1985：48-50.

[15]谢敬东，唐国庆，徐高飞.组合预测方法在电力负荷预测中的应用[J].中国电力，1998，31（6）：3-5.

[16]李振亮.组合预测方法在大气环境评价中的应用[J].数理统计与管理，1997，16（4）：12-15.

[17]王居平.组合预测方法及在图书馆管理中的应用[J].情报杂志，2002（8）：61-63.

[18]袁文华，鄂加强，龚金科，等.柴油机连杆轴颈磨损量组合预测模型及应用[J].湖南大学学报：自然科学版，2006，33（3）：71-74.

[19]张克中，毛树华，袁卫红.马尔科夫残差修正灰色模型及其在公路网规划中的应用[J].武汉理工大学学报：交通科学与工程版，2005，29（4）：503-505.

The EPS torque angle sensor reliability prediction based on combination model

MA Jun
（Automobile School，Beijing Polytechnic，Beijing 100026，China）

To improve the electric power steering system performance，designed a kind of electric power steering system torque angle sensors，and establish the mathematical model to estimate the reliability of the sensor.On the basis of experiment comparing the grey GM（1，1）model and residual correction gray GM（1，1）model and the prediction accuracy of gray Markov chains model residuals amended.Because a single model is difficult to ensure the prediction accuracy level，so by calculating the combined model different steps transition probability matrix determines the target state，then get the predicted value.By comparison，combination model is better than a single model of precision，but also the question of appropriate description randomness.

torque angle sensors；grey GM（1，1）model；residual error correction；Markov chain

A

：1674-5124（2015）07-0080-05

10.11857/j.issn.1674-5124.2015.07.019

2014-10-10；

：2014-12-18

北京高等学校“青年英才计划”资助项目（YETP1798）

马峻（1980-），男，天津市人，讲师，硕士，研究方向为汽车制造技术、EPS技术。