基于小波变换的盆地沉积-构造波动分析

赵 利，李 理，董大伟

中国石油大学(华东) 地球科学与技术学院，山东 青岛 266580



基于小波变换的盆地沉积-构造波动分析

赵 利，李 理，董大伟

中国石油大学(华东) 地球科学与技术学院，山东 青岛 266580

波动分析是一种定量研究盆地沉积-构造演化的方法。本文分析了滑动窗口法在盆地沉积波动分析数理方法中的诸多不足，采用小波变换的多尺度分解思想对研究区19个点处的信号做了处理，方法是使用db4小波对沉积速率直方图做Level9次分解。结果表明：以东营凹陷616-2点为例做沉积波动分析发现，通过小波变换可以获得能量波(A)、次能量波(n)、沉积演化波(g)和高频波(l)四个分解波，其中周期波n、g、l的周期分别是91、50、14 Ma；平面对比各分解波发现，能量波反映的是盆地沉积的整体趋势和盆内某点的平均沉积速率，次能量波反映的是盆地构造演化周期和断陷结构，沉积演化波反映的是板块聚敛控制下的盆地沉积-剥蚀演化，沉积干涉波反映的是盆地多尺度周期波叠加所呈现的地层沉积速率；空间尺度波动分析表明，一期构造运动会在空间内产生一个特定的构造波，而多个构造波在空间内会有规律地相互干涉，即产生多期构造叠加。

小波变换；分解波；波动分析；沉积盆地；东营凹陷

0 引言

众所周知，许多地质事件、现象在地质历史时期内的变化具有明显的周期性、韵律性。根据分形系统或观察尺度的不同，前人对这些现象做了细致的研究，如季候纹泥或叠层石的周期性变化、层序地层学中的旋回分析、镶嵌构造和地壳波浪运动等[1-3]。施比伊曼等[4]在研究盆地沉积速度时发现，沉积速度曲线是由若干周期性波动过程叠加而成的，并建立了盆地内沉积波动过程的分析方法；随后，金之钧等[5]将该方法引进到国内以研究盆地内沉积的发展、演化，以及构造迁移。之后，众多学者将该方法完善并应用到沉积中心迁移、剥蚀过程分析及剥蚀量计算、高频波动与油气成藏耦合等研究当中[6-11]。

当我们研究上述周期性时，会面临两个问题：一是如何将周期性波动用地质参数进行表征；二是地质现象非常复杂，观察到的描述性数据是经过多种类型、多尺度波动叠加的，应采用哪种数理方法从地质参数中分解出我们所需要的周期性波动信号。在研究过程中，前人一致采用沉积速率直方图来表征盆地的沉积波动，以解决第一个问题。对于第二个问题，施比伊曼等[4]最早采用滑动窗口法来获取多个波函数。但该方法由手工操作，过程复杂，人为因素大。李京昌等[6]采用三次样条差值法平滑沉积速率直方图后，再利用傅里叶变换提取沉积速率曲线的几个主周期，最后还是利用滑动窗口法分解曲线，整个过程实现了计算机自动化处理；国内学者继而研发了波动过程分析软件[7-8]。然而，这种数理方法在信号处理当中具有相当大的局限性，对地质现象的解释也会出现偏差。本文立足于盆地沉积波动理论，采用信号处理中更为先进的小波变换方法来替代前人的数学处理方法，以解决上述问题；在此基础上，从点、面、体三个逐步递进的方面来论述盆地在时间域、空间域上的沉积-构造波动，以期对盆地波动分析理论及其应用做出一定的补充和完善。

1 滑动窗口法的局限性与小波变换

如果把周期性地质事件对沉积的控制当成信号来看，现今观察到的地层沉积速率就是各种地质作用叠合后输出的合成信号。通过信号处理方法把合成信号中含有的周期成分抽取出来，这就是盆地沉积波动分析的目的。而且，前人统一采用滑动窗口法作为信号处理的数学方法，其思想表示如下：首先，使用大窗口将各组段地层沉积速率滑动平均出一系列散点，并连接散点成平滑的曲线A(低频)；然后，使用较小的窗口以获取曲线N(相对高频)；当曲线A与N之差是周期曲线n，即N=n+A时，则称n为周期波(如果n不具有周期性，则不断调节窗口以获得这个周期波)；再次调小窗口以获取曲线G，且满足G=g+N，其中g也是周期波；重复上述过程，以获得下一个周期波l，即L=l+G[4-6]。其中，上述周期波n、g、l是时间的函数，且频率逐渐变大。

然而，滑动窗口法的局限性及其对地质现象解释的偏差可以做以下分析：

1)滑动窗口法得到的是信号n、g、l在整个时间域内的整体变换，使得这种变换缺乏时间和频率的定位功能，即无法获得某一频率出现的时刻信息。也就是说，滑动窗口法获得的波函数不能反映某一构造运动出现的时间，以及这一构造运动结束的时间。

2)n、g、l是单变量t的函数，信号分解得到的周期函数不随时间的变化而变化，使得滑动窗口法多适用于平稳信号的处理。在地质演化过程中，沉积盆地内的一期构造运动结束之后会叠加上另一期构造运动，从而形成多期叠合盆地，即当第一期周期波n1(能够指示该构造运动特征的周期函数)终止时，会续接上第二期周期波n2或l1。但是，滑动窗口法分解得到的周期波----构造运动的特征函数会存在于整个时间域并影响整个沉积过程，导致特征函数不能反映构造运动随时间的变化。此外，对于许多地质事件而言，其变化往往不具有稳定性，常表现为在均变过程中伴以突变或终止，如板块俯冲方向的变化、岩浆活动等。因此，滑动窗口法不适于处理从地质事件中提取的信号。

3)滑动窗口法在时域分析中，时域窗和频域窗乘积恒定且大于等于1/2，即在同时获取高的时频分辨率时变为不可能[12]。这对于寻找波动方程而言，在获得n、g之后，l以及更高频率周期波的准确性就会降低。

4)前人在利用滑动窗口法分解波动方程时需要手工绘制，对结果的准确度影响非常大；之后有学者实现了计算机的自动处理，但程序编制仍会在一定程度上增加获取波动方程的难度[6，9]。

上述出现的数理问题及对应的实际问题在信号处理的应用史上同样出现过，数学家们为此发明了具有良好时域和频域定位能力的小波变换法。其思想是提供一个由各种低通及高通滤波器组成的滤波器组，通过伸缩平移的方式对信号不同尺度(频率)上的分量进行分解，以获得多尺度周期波函数[13]。这样，前面提到的问题就都迎刃而解了。此外，小波分析获得的波函数没有解析解，它的预测功能可以通过分形几何的自相似性加以实现[14]。

2 沉积波动曲线建立

笔者将以东营凹陷为例，对小波变换方法的具体应用加以说明。研究区是渤海湾盆地济阳坳陷的亚一级构造单元，东临郯庐断裂带，南与鲁西隆起相接，西连惠民凹陷，北以陈南断层为界，与沾化凹陷相间以陈家庄凸起，是具有北断南超特点的典型半地堑(图1)。东营凹陷东西长约90 km，南北宽约 65 km，是济阳坳陷内最富油气资源的一个凹陷。

东营凹陷基底由太古宇变质岩基底和古生界地台构造层组成，盖层由中生界和新生界组成。中生界发育上侏罗统--白垩系碎屑岩和火山碎屑岩，发育有坊子组、三台组、蒙阴组、西洼组以及王氏组、卞桥组，地层受燕山运动影响沉积于NW向断陷盆地阶段。新生界以湖湘碎屑岩为主，地层发育完整，包括孔店组(Ek)、沙河街组(Es)、东营组(Ed)、馆陶组(Ng)、明化镇组(Nm)和平原组(Q1p)，地层受喜马拉雅运动影响分别经历了近EW向断陷阶段、NE向断陷阶段和热沉降阶段(图2)。

本研究在东营凹陷内共选取了19点进行基于小波变换的沉积波动分析，并以616-2点为例阐述该方法。资料准备阶段与前人研究方法一样，即首先建立研究区的地层年龄格架，确立时间参数；然后，统计构造剖面上的现今地层观察厚度，通过去压实校正获得地层原始厚度，而压实系数与深度的关系采用不同构造带内已知数据点拟合的公式[16]；最终，可以得到以时间为横轴，以地层沉积速率为纵轴的直方图(图2)。沉积波动曲线建立阶段，本研究经过调试后采用db4小波对沉积速率直方图做Level9次分解，结果如图2所示。图2中，A曲线整体为正值，随时间演化平缓上升，指示东营凹陷在新生代整体持续沉降，沉积速率随时间缓慢增大。因此，该曲线代表一个盆地地质历史时期的总体升降趋势，故称为能量波。晚白垩世以来，东营凹陷是主动裂陷机制下的盆地，构造演化经历热隆起(K2--Ek3)--伸展断陷(Ek2--Ed)--热沉降(N--Q)三个阶段，约95 Ma[17]。而n曲线正向半波段与盆地强烈断陷沉积阶段对应，负向半波段与平缓热沉降阶段对应，符合构造演化周期，故称之为构造波，也称为次能量波。g曲线正值区对应高沉积速率时期，曲线负值区对应低沉积速率或沉积间断时期，这与沉积速率的整体变化趋势具有非常好的一致性，故称之为沉积演化波。l曲线周期小、频率大，与其他点的曲线没有对比规律，推测该曲线对应二、三级断层控制的沉积演化，故称之为高频波。L曲线是将能量波、次能量波、沉积演化波、高频波叠加后的曲线，属于沉积速率直方图的沉积波动方程，称之为干涉波。N、G、L与A、n、g、l曲线的关系如小波分解的树枝模型所示，其中N=A+n，G=N+g，L=G+l(图2)。

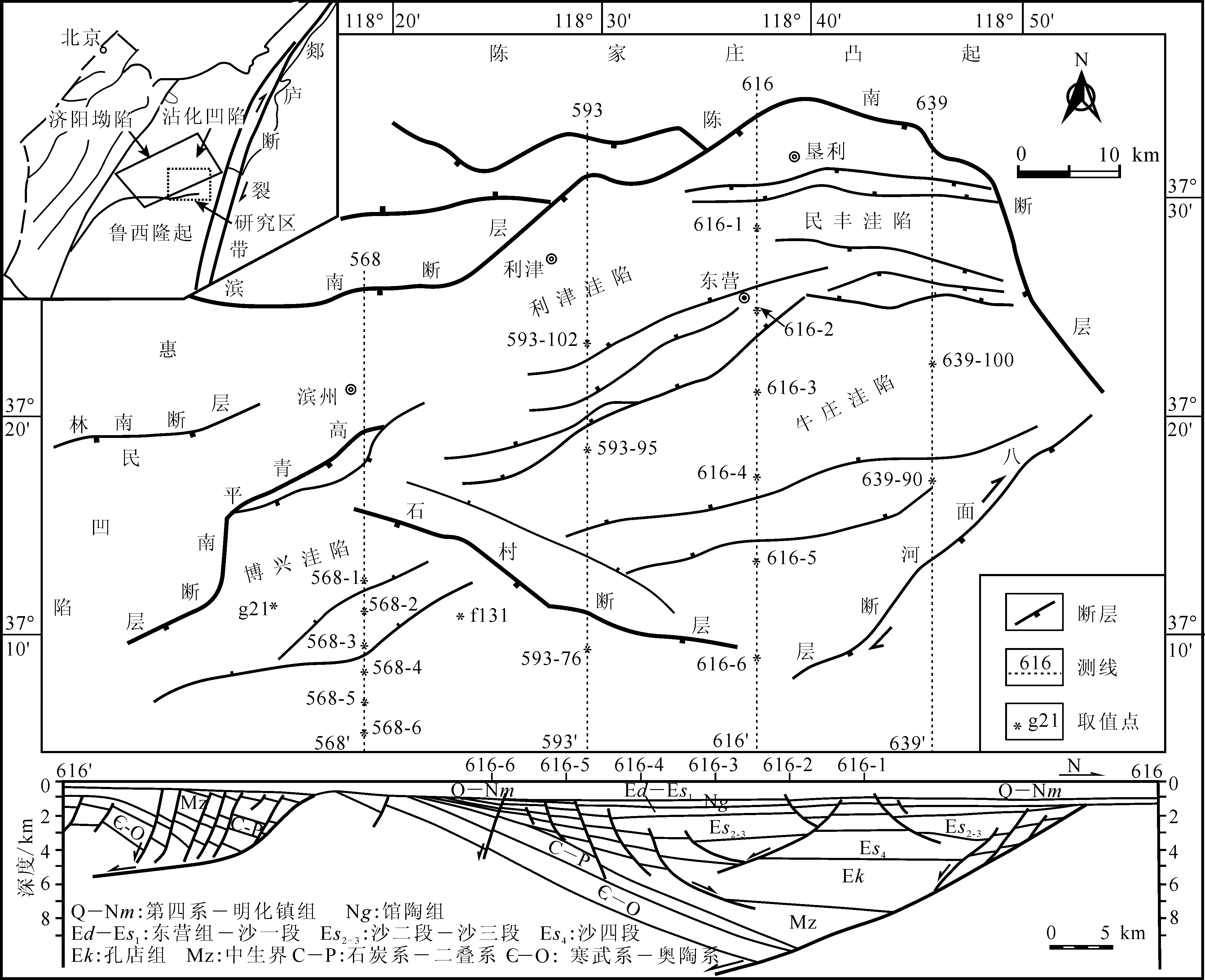
据文献[15]修编。图1 东营凹陷构造简图Fig.1 Simplified geological map of Dongying sag

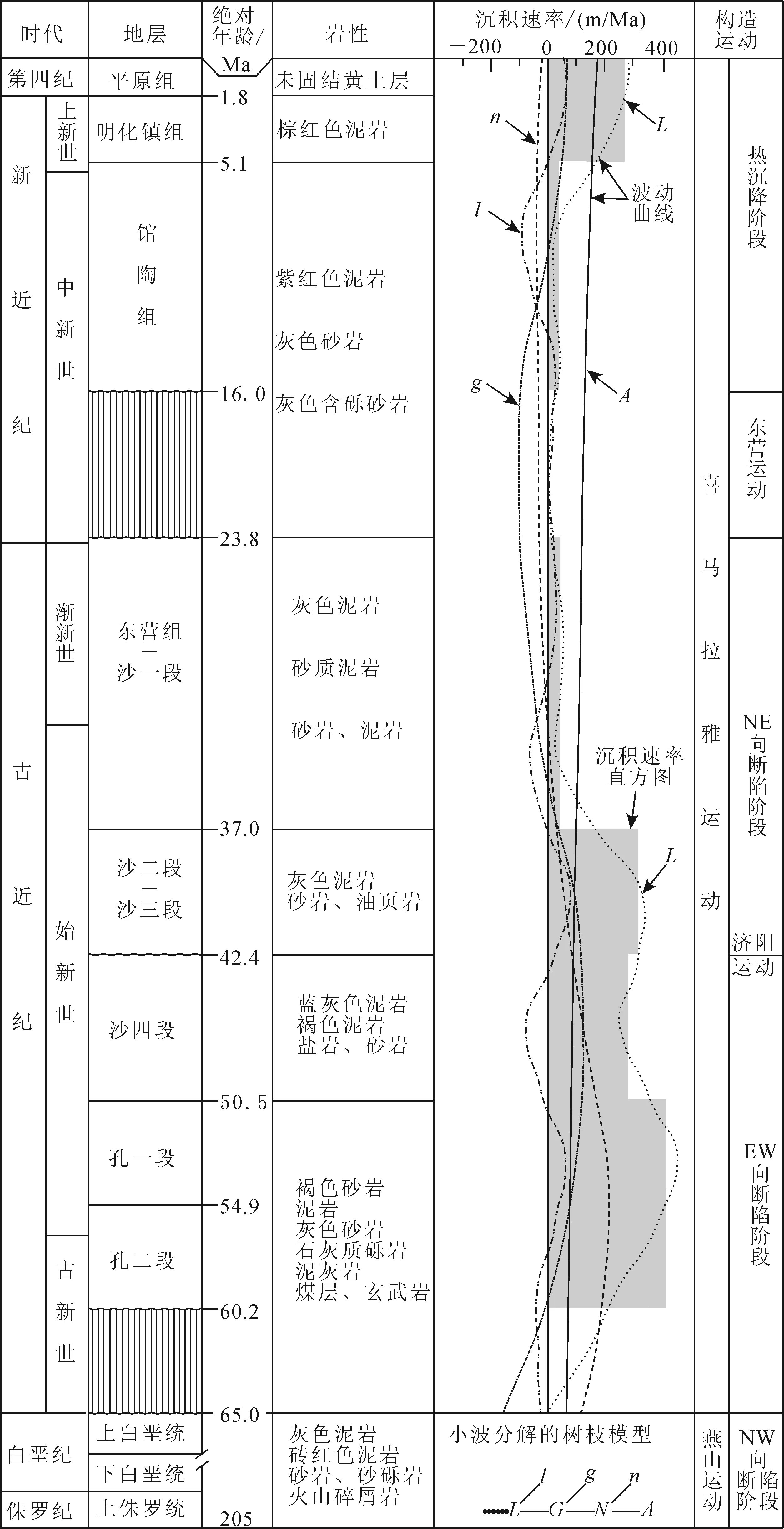
A.从沉积速率直方图中提取完各种周期波后剩余的曲线；n.从沉积速率直方图中提取出的周期为91 Ma的曲线；g.从沉积速率直方图中提取出的周期为50 Ma的曲线；l.从沉积速率直方图中提取出的周期为14 Ma的曲线；L.A、n、g、l曲线叠加后的曲线。图2 东营凹陷616-2点(位置见图1)沉积波动特征图Fig.2 Sedimentary wave analysis for point 616-2 (location in Fig.1) in Dongying sag

3 波动曲线平面特征分析

平面上对比所获得的各分解波或沉积波都可以分析其时空变化规律，进而指示对应的地质过程。能量波(A)是经过小波变换的多次分解之后得到的一条简单曲线，它是周期最长的波，反映的是盆地地质历史时期内的整体沉积趋势，受控于盆地所处的构造环境或盆地类型，控制着盆地内各点的平均沉积速率。从图3a中可以看出，所有19个位置点处的能量波曲线形态近乎相同，彼此近于平行；这表明同一坳陷内能量波相同，只是不同点处平均沉积速率不同。需要指出的是，每条曲线值从65 Ma开始逐渐增大，但变化不大，反映的是盆地平均沉积速率，亦可作为沉积速率背景值。

从图3b中可以看出：这6条曲线变化趋势相似，所有曲线的正向半波段处于65～23 Ma，负向半波段处于23～0 Ma，这分别对应盆地断陷阶段和拗陷阶段；随着位置点逐渐远离洼陷区(图1中位置点616-1→616-6)，各次能量波振幅逐渐减小，体现出单断式的东营凹陷地层北厚南薄沉积特征和北断南超的盆地结构。因此，次能量波(n)反映的是盆地构造演化周期和断陷结构，推测其受控于裂陷盆地演化规律和内部控盆断层发育位置。

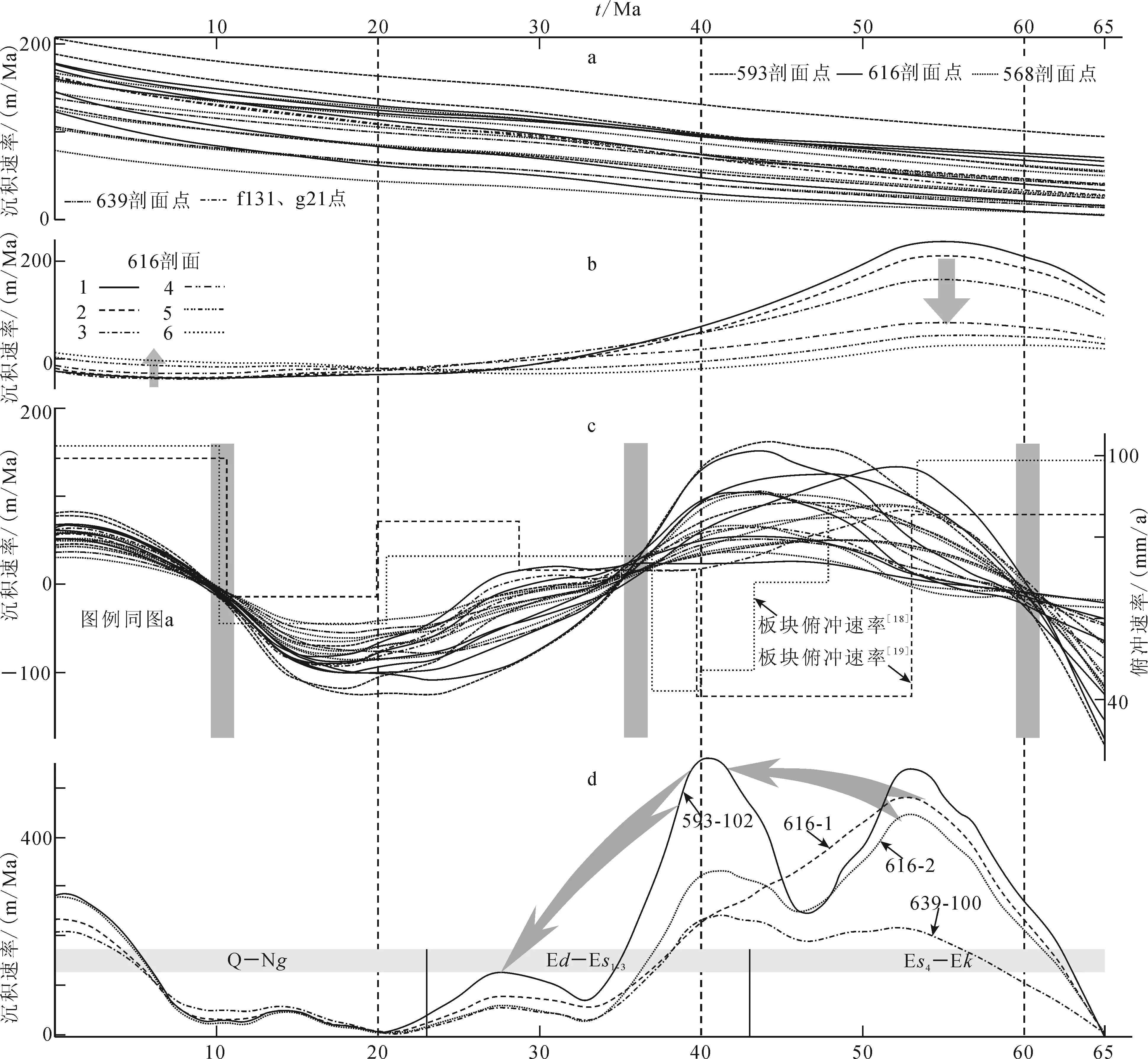
a. 所有19个位置处的能量波对比；b. 点616-1--616-6位置上的次能量波对比；c. 所有19个位置处沉积演化波与太平洋板块俯冲速率的对应关系；d. 牛庄--民丰--利津洼陷内4个位置处L波对比(位置见图1)。图3 分解波在平面上的对比Fig.3 Comparisons of wave decompositions in the plane

从图3c中可以看出：沉积演化波g的值与板块俯冲速率成反比，峰谷区与东营凹陷所经历的强烈断陷沉积、断陷萎缩沉积、拗陷整体沉积三个阶段对应：60 Ma，凹陷开始进入新生代快速沉积阶段，沉积波波处于波峰期，板块俯冲速度由85～99 mm/a减小到约41 mm/a；36 Ma，盆地进入整体沉积速率低值时期，沉积波开始进入波谷，板块俯冲速度增大到72～84 mm/a；10 Ma，虽然盆地沉积波进入波峰，但整体沉积速率不大，盆地进入整体拗陷阶段，板块俯冲速度增大到约100 mm/a[18-19]。因此，沉积演化波(g)反映的是盆地沉积-剥蚀演化，其受控于板块聚敛速度的变化，控制着地质历史时期内某位置处各组段地层的相对沉积速率。

沉积波动法获取的干涉波曲线还可以反映盆地沉积中心的迁移，近年来众多学者在黄骅坳陷、塔里木盆地等地区已做过应用[5，11]。图3d表示的是牛庄洼陷--民丰洼陷--利津洼陷的4条L波曲线对比，而L波曲线是由A、n、g、l四条波曲线叠加而成。从图3d中可以清楚地看出，EW向断陷阶段(Es4--Ek)凹陷沉积中心位于民丰洼陷(616-1、616-2点)、利津洼陷(593-102点)，NE向裂陷阶段(Ed--Es1--3)凹陷沉积中心主要位于利津洼陷(593-102点)，热沉降阶段(Q--Ng)凹陷整体沉降。上述过程与前人研究是完全吻合的[20]。

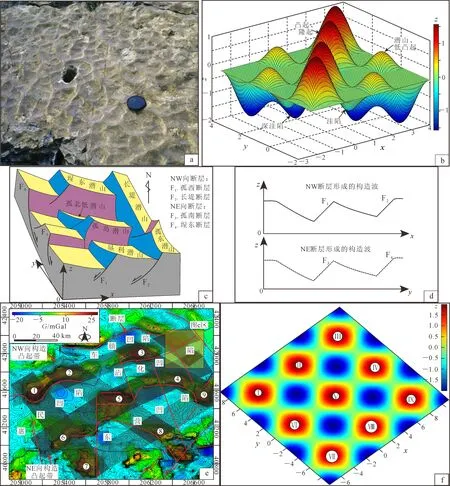
a.干涉波痕野外照片[21]；b.干涉波z=sinxsiny+sin2xsin2y三维图；c.沾化凹陷潜山发育图[22](位置见图4e)；d.图4c分解出的两个构造波；e.济阳坳陷重力异常图[23-24](位置见图1):1.宁津凸起,2.无棣凸起,3.义和庄凸起,4.陈家庄凸起,5.滨县凸起,6.青城凸起,7.磁村凸起,8.广饶凸起,9.青坨子凸起；f.干涉波z=sinx+sin(y+0.5π)平面图:Ⅰ-Ⅸ.高z值区。G为重力场强度。毫伽(mGal)为非法定计量单位，1 mGal=10-6 m/s2。图4 两期构造叠加示意图Fig.4 Diagram of two phases’ structural overlapping

4 空间尺度波动----构造波动分析

空间尺度的波动分析从构造形迹的研究入手，即一期构造运动常会在空间内产生多个相似的的构造形迹，通过定性和定量描述这些有规律的构造行迹可以建立一个空间立体波[6]。当多期构造运动叠加时，多个空间立体波同样会发生干涉，从而形成所谓的构造波动。地质中最典型的实例就是干涉波痕(图4a)。上述干涉过程是按一定规律进行的，用地质语言表述为：若第一期构造运动形成的凸起在第二期构造运动中仍处于构造凸起位置上，则该位置形成大的凸起或隆起；若第一期构造运动形成的凸起在第二期构造运动中却处于构造凹陷位置上，或反过来，则该位置形成潜山或低凸起；若第一期构造运动形成的凹陷在第二期构造运动中仍处于构造凹陷位置上，则该位置形成大的洼陷或深洼陷。数学模型表述为：函数z1=sinxsiny的波峰与函数z2=sin2xsin2y的波峰相叠加形成高峰值区，z1的波峰与z2的波谷或z1的波谷与z2的波峰相叠加形成低峰或浅谷值区，z1的波谷与z2的波谷相叠加形成深谷值区(图4b)。

前人曾根据沾化凹陷两期断层发育建立了潜山构造叠加模型(图4c)：晚侏罗世--白垩纪，NE向伸展应力场下发育的孤西断层(F1)、长堤断层(F2)发生掀斜运动，形成了两组NW向展布的断块型潜山；古近纪，该区应力场转变为NW向伸展，NE向发育的孤南断层(F3)、埕东断层(F4)等切割前期断层，其掀斜活动将前期潜山切割、改造并定型，形成“网格分布的格局”[22]。对该区建立三维坐标系并分解其构造过程，可以看出：xz平面上的构造波是晚侏罗世--白垩纪发育的F1、F2断层产生的，其NE向的传播方向为该时期应力场伸展方向；yz平面上的构造波是古近纪发育的F3、F4断层产生的，其NW向的传播方向为该时期应力场伸展方向(图4d)。

同理，笔者根据济阳坳陷断层发育和凸起、凹陷的分布情况建立了构造叠加模型(图4e)及其对应的数学模型(图4f)。构造模型的建立首先需要确定空间波的个数和传播方向，这需要根据研究区构造演化史、断裂发育情况等因素确定[6]。晚中生代以来，济阳坳陷属于多期伸展型叠加盆地[22-23]。晚侏罗--早白垩世期间，坳陷受控于郯庐断裂左旋活动，其内多条NW向断层控制构造格局；晚白垩世期间虽然其发生构造发转，但对构造格局影响不大；进入新生代，郯庐断裂受印度板块远程效应、太平洋板块俯冲方向改变等因素影响由左旋活动逐渐变为右旋，控凹断层也由NW向断层逐步变为NE向断层(图2)[15，20, 22-23]。此外，结合济阳坳陷重力异常图及以上分析，济阳坳陷在晚中生代以来共发育两个空间波：晚侏罗--早白垩世NE向传播NW向展布的空间波，即由NW走向的F1、F2断层形成的；早始新世以来NW向传播NE向展布的空间波，即由NE走向的F3、F4断层形成的(图4c、d)。

通过上述分析我们可以建立一个数学模型与济阳坳陷的构造模型进行匹配分析：如果早期NE向传播NW向展布的构造采用空间波z1=sin(y+0.5π)表示，后期NW向传播NE向展布的构造采用空间波z2=sinx表示，那么现今观察到的凸起、凹陷分布就可以用干涉波z=sinx+sin(y+0.5π)示意。以凸起为例对比发现，两者具有很好的对应性：图4e中的高重力异常区1--9分别对应图4f中的高z值区Ⅰ--Ⅸ，即分别为宁津凸起、无棣凸起、义和庄凸起、陈家庄凸起、滨县凸起、青城凸起、磁村凸起、广饶凸起和青坨子凸起。当然，相邻凸起之间会形成低凸起、潜山，如5(Ⅴ)和6(Ⅵ)之间的高青--平方王潜山；对角凸起之间会形成洼陷，如6(Ⅵ)和8(Ⅷ)之间的博兴洼陷。

5 结论

为解决沉积波动中滑动窗口法在滤波过程中存在的缺陷，笔者提出了小波变换的数理方法用于多尺度分解沉积波动曲线，并以东营凹陷为例解析了各波动曲线所指示的地质意义，得到的主要成果、认识如下：

1)盆地沉积历史时期内的不同周期波叠加产生非严格周期波，经小波变换的方法可以准确、高效地从多尺度分解出不同周期波，解决滑动窗口法在数学处理过程中的不足。

2)以东营凹陷616-2点为例做沉积波动分析表明，通过小波变换可以获得能量波(A)、次能量波(n)、沉积演化波(g)和高频波(l)四个分解波，其中周期波n、g、l的周期分别是91、50、14 Ma。

3)平面对比各分解波发现，能量波反映的是盆地沉积的整体趋势和盆内某点的平均沉积速率，次能量波反映的是盆地构造演化周期和断陷结构，沉积演化波反映的是板块聚敛控制的盆地沉积-剥蚀演化，沉积干涉波反映的是盆地多尺度周期波叠加所呈现的地层沉积速率。

4)空间尺度波动分析表明，一期构造运动会在空间内产生一个特定的构造波，而多个构造波在空间内会有规律地相互干涉，即产生多期构造叠加。如济阳坳陷晚侏罗世--早白垩世的NW向构造与新生代的NE向构造叠合。

本文得到了中国石油大学(华东)信息与控制工程学院孙伟峰老师有益的指导，在此表示感谢。

[1] 赵庆乐，张世红，王婷婷，等. 利用Matlab函数识别沉积物中的米兰柯维奇旋回信号[J]. 吉林大学学报：地球科学版，2010，40(5)：1217-1220. Zhao Qingyue, Zhang Shihong, Wang Tingting, et al. Recognition of Milankovitch Cycles in Sediments by Using Matlab Functions[J]. Journal of Jilin University: Earth Science Edition, 2010, 40(5): 1217-1220.

[2] 张伯声，王战. 中国的镶嵌构造与地壳波浪运动[J]. 西北大学学报，1974，4(1)：1-11. Zhang Bosheng, Wang Zhan. Mosaic Structures and Wave Motion of the Crust in China[J]. Journal of Northwest University, 1974, 4(1): 1-11.

[3] 张一伟. 山东西部箕状凹陷形成的探讨：初论地壳波浪运动[J]. 石油学报，1983，4(4)：19-25. Zhang Yiwei. On the Formation of Dustpan-Shaped Depressions in the Western Part of Shandong: A Preliminary Discussion on Wave-Link Crustal Movement[J]. Acta Petrolei Sinica, 1983, 4(4): 19-25.

[4] 施比伊曼 B И，张一伟，金之钧，等. 波动地质学在黄骅坳陷演化分析中的应用：再论地壳波状运动[J]. 石油学报，1994，15(增刊)：19-25. Shpilman V, Zhang Yiwei, Jin Zhijun, et al. The Application of Wave Geology in Basin Analysis in Huanghua Depression[J]. Acta Petrolei Sinica, 1994, 15(Sup.): 19-25.

[5] 金之钧，张一伟，刘国臣，等. 沉积盆地物理分析：波动分析[J]. 地质论评，1996，42(增刊)：170-180. Jin Zhijun, Zhang Yiwei, Liu Guochen, et al. Physical Analysis Method for Sedimentary Basin: Wave Analysis[J]. Geological Review, 1996, 42(Sup.):170-180.

[6] 李京昌，金之钧，孙强. 盆地波动分析中的数学模型及计算机实现[J]. 地质论评，1996，42(增刊)：276-282. Li Jingchang, Jin Zhijun, Sun Qiang. Numerical Model and Its Computerization for Wave Analysis in Basin Study[J]. Geological Review, 1996, 42(Sup.)：276-282.

[7] 李儒峰，郭彤楼，陈国飞，等. 米仓山前陆冲断带波动特征与构造沉积演化[J]. 中国科学：D辑，2008，38(增刊I)：63-69. Li Rufeng, Guo Tonglou, Chen Guofei, et al. The Wave Analysis and Tectonic-Sedimentary Evolution for the Foreland Thrust Belt in Micangshan[J]. Science China: Series D, 2008, 38(Sup. I):63-69.

[8] 李儒峰，金之钧，马永生，等. 盆地波动特征与生储盖层耦合关系分析：以楚雄盆地为例[J]. 沉积学报，2004，22(3)：474-480. Li Rufeng, Jin Zhijun, Ma Yongsheng, et al. Analysis for the Coupling Relationship Between Basin Wave Characteristics and Source, Reservoir and Cap Rocks: A Case Study of Chuxiong Basin,Yunnan[J]. Acta Sedimentologica Sinica, 2004, 22(3): 474-480.

[9] 李儒峰，马永生，汤良杰，等. 云南楚雄盆地波动特征及构造沉积演化[J]. 地球科学：中国地质大学学报，2004，29(3)：309-316. Li Rufeng, Ma Yongsheng, Tang Liangjie, et al. Wave Characteristics and Tectonic-Sedimentation Evolution of Chuxiong Basin in Yunnan Province[J]. Earth Science: Journal of China University of Geosciences, 2004, 29(3):309-316.

[10] 陈书平，金之钧，孙海龙. 库车前陆区中--新生代盆山波动耦合[J]. 西安石油大学学报：自然科学版，2004，19(4)：24-28. Chen Shuping, Jin Zhijun, Sun Hailong. Mesozoic-Cenozoic Basin-Mountain Wave Coupling in Kuche Foreland[J]. Journal of Xi’an Shiyou University: Natural Science Edition, 2004, 19(4): 24-28.

[11] 金之钧，张一伟，陈书平. 塔里木盆地构造-沉积波动过程[J]. 中国科学：D辑，2005，35(6)：530-539. Jin Zhijun, Zhang Yiwei, Chen Shuping. The Tectonic-Sedimentary Wave Analysis in Tarim Basin[J]. Science China: Series D, 2005, 35(6): 530-539.

[12] 马耀庭，邵毅全. 傅里叶变换在应用中的局限性及克服方法[J]. 内江师范学院学报，2008，32(12)：42-44. Ma Yaoting, Shao Yiquan. The Limitation of Fourier Transform in Practice and the Methods of Solution[J]. Journal of Neijiang Normal University, 2008, 32(12): 42-44.

[13] 李琪，林云芳，曾小苹. 应用小波变换提取张北地震的震磁效应[J]. 地球物理学报，2006，49(3)：855-863. Li Qi, Lin Yunfang, Zeng Xiaoping. Wavelet Analysis as a Tool for Revealing Geomagnetic Precursors of the Zhangbei Earthquake[J]. Chinese Journal of Geophysics, 2006, 49(3): 855-863.

[14] 杜建卫，王超峰. 小波分析方法在金融股票数据中的应用[J]. 数学的实践与认识，2008，38(7)：68-75. Du Jianwei, Wang Chaofeng. Application of the Wavelet Transformatio in Financial Data Processing[J]. Mathematicsin Practice and Theory, 2008, 38(7): 68-75.

[15] 唐其升. 东营凹陷断裂系统与中央构造带形成机制[D]. 杭州：浙江大学，2007. Tang Qisheng. The Fault System and Formation Mechanism of Central Structural Zone in Dongying Sag[D]. Hangzhou：Zhejiang University, 2007.

[16] 边凤青. 东营沙四段--孔店组剥蚀厚度与原型盆地的恢复[D]. 青岛：中国海洋大学，2009. Bian Fengqing. The Restored Eroded Thickness and Prototype Basin of Kongdian Formation and the Fourth Member of the Shahejie Formation in Dongying Depression[D].Qingdao：Ocean University of China, 2009.

[17] 漆家福，张一伟，陆克政，等. 渤海湾新生代裂陷盆地的伸展模式及其动力学过程[J]. 石油实验地质，1995，17(4)：316-323. Qi Jiafu, Zhang Yiwei, Lu Kezheng, et al. Extensional Pattern and Dynamic Process of Cenozoic Rifting Basin in the Bohai Bay[J]. Petroleum Geology and Experiment, 1995, 17(4): 316-323.

[18] Engebretson D C, Cox A, Gordon R G. Relative Motions Between Oceanic and Continental Plates in the Pacific Basin[J]. Geological Society of America Special Papers, 1985, 206: 1-59.

[19] Nothrup C J, Royden L H, Burchfiel B C.Motion of the Pacific Plate Relative to Eurasia and Its Potential Relation to Cenozoic Extension Along the Eastern Margin of Eurasia[J]. Geology, 1995, 23(8): 719-722.

[20] 任建业. 渤海湾盆地东营凹陷S6’界面的构造变革意义[J]. 地球科学：中国地质大学学报，2004，29(1)：69-76. Ren Jianye. Tectonic Significance of S6’ Boundary in Dongying Depression, Bohai Gulf Basin[J]. Earth Science: Journal of China University of Geoscience, 2004, 29(1): 69-76.

[21] Baker R G. Interference Ripple Marks[EB/OL]. [2007-08-31]. http://digital.lib.uiowa.edu/cdm/singleitem/collection/ geoscience/id/2793.

[22] 林会喜，方旭庆，李凌，等. 鲁北济阳坳陷沾化凹陷东部潜山的发育及油气成藏富集规律[J]. 地质通报，2006，25(9/10)：1160-1167. Lin Huixi, Fang Xuqing, Li Ling, et al. Development of Buried Hills of the Eastern Zhanhua Subbasin, Jiyang Depression, Northern Shandong, China and Controlling Factors of the Formation of Petro-leum Accumulations[J]. Geological Bulletin of China, 2006, 25(9/10):1160-1167.

[23] 王国芝. 济阳坳陷陈家庄--白庙地区构造成因及演化研究[D]. 东营：胜利油田博士后科研工作站，2006. Wang Guozhi. Tectonic Origin and Evolution of Chenjiazhuang-Baimiao Area in Jiyang Depression, Eastern China[D]. Dongying: Post-Doctoral Research Center in Shengli Oil Field, 2006.

[24] 陈海云，林春明，闫汉杰，等. 重力资料在济阳坳陷石油勘探中的应用[J]. 石油学报，2005，26(6)：46-51. Chen Haiyun, Lin Chunming, Yan Hanjie, et al. Application of Gravity Data to Petroleum Exploration in Jiyang Depression[J]. Acta Petroleum Sinica, 2005, 26(6):46-51.

Basin’s Sedimentary-Tectonic Wave Analysis Based on Wavelet Transform

Zhao Li，Li Li, Dong Dawei

SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,Shandong,China

The wave analysis is a kind of quantitative approach to basins’ sedimentary-tectonic evolution. The authors analyze the mathematical defects of sliding-window method in the process of sedimentary wave analysis. In order to figure out the problems, we take 19 cases to apply the wavelet transform according to the multi-scale decomposition idea. The method is to use db4 wavelet to decompose the deposition rate histogram in level 9. The results show that we can get energy wave(A), second energy wave(n), sedimentary wave(g), and high-frequency wave(l) by using wavelet transform with taking case Dongying sag 616-2 as an example. The period of decomposed waves are 91 Ma (n), 50 Ma (g), 14 Ma (l). In comparison of the waves in the plane, we found that the energy waves reflect the overall depositional trend or the average deposition rate, the secondary energy waves reflect the tectonic cycle and the structure of the rifting basin, the sedimentary waves reflect the sedimentary-denudation evolution controlled by plate convergence, and the sedimentary interference waves present the sedimentary rate curve superimposed by multi-scale waves. Based on the analysis in spatial domain, we found that a period of tectonic movement produced a special structural wave. Geologically speaking, structural overlaps can be inferred from the interference of several structural waves.

wavelet transform; wave decompositions; wave analysis; sedimentary basin; Dongying sag

10.13278/j.cnki.jjuese.201504302.

2014-11-17

国家自然科学基金项目(40772132)

赵利(1988--)，男，博士研究生，主要从事油区构造解析的研究，E-mail:orchidy@126.com。

10.13278/j.cnki.jjuese.201504302

P631.4

A

赵利，李理，董大伟. 基于小波变换的盆地沉积-构造波动分析.吉林大学学报:地球科学版,2015,45(4):1227-1236.

Zhao Li, Li Li, Dong Dawei. Basin's Sedimentary-Tectonic Wave Analysis Based on Wavelet Transform.Journal of Jilin University:Earth Science Edition,2015,45(4):1227-1236.doi:10.13278/j.cnki.jjuese.201504302.