基于电磁场理论的变电站控制电缆安全性分析

王 磊，李 艳，杨 扬

(东北电力大学 电气工程学院，吉林 吉林 132012)

变电站接地的安全性和可靠性是电力系统的一个重要问题，接地能否起到应有的作用直接关系到电气设备和人身的安全。

特、超高压输电线路工程需要相应的变电站与之配套。但同时也要注意，变电站内及附近发生雷击事故时，暂态雷电流注入地网，地电位升急剧升高，进而布置在变电站内用于通讯和控制的控制电缆将遭受严重的影响。

对此，本文提出一种新型接地导体电磁场等效方法，建立了相应的数学模型，计算控制电缆芯皮电位差，同时计算各个参数对控制电缆芯皮电位差的影响，测量出控制电缆耐受电压和计算出GPR的限值。

1 控制电缆芯皮电位差计算

1.1 水平多层土壤接地导体的电磁场模型

根据多层土壤的边界条件，针对控制电缆相连的每一根接地导体的点源在每一个电磁场点处产生的电位，分别传递推理该电磁场点处的格林函数［1］数值序列，应用数学计算方法拟合该点处的格林函数，得到接地导体在电磁场处的点电位，最终测量出控制电缆的芯皮电位差。

置于多层水平土壤接地导体的模型如图1所示。在球面坐标系下，接地导体中任意点的电位Φi满足泊松方程［3］:

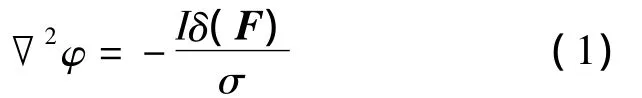
式中:σ为控F接地导体的电导率;F为场点的矢量;δ(F)为狄拉克δ函数。

图1 置于多层土壤中接地导体的模型Fig.1 Put in multi－layer soil earthing conductor model

由于泊松方程是描述静电场电位函数φ与其源(电荷)之间关系的微分方程，因此通过圆柱型坐标系，可将式(1)改写为

根据分离变量法［4］将式(2)化简成常微分方程，设 φ(x，z)=θ(x)φ(z)，则有

式中:J0(λx)、Y0(λx)为不同类的零阶贝塞尔函数;A1(λ)、A2(λ)、B1(λ)、B2(λ)为 λ 的函数。

由理论推理，B2(λ)必须为零，进而得到拉普拉斯方程的通解为

其中

式(3)可以看为是无穷项相叠加，从而可以得到有点源的电位格林函数表达式为

第一层场点电位记做Φ1，第二层场点电位记做Φ2，最终得到土壤水平各层的边界条件:

当电位Φn(x，z)=0时，z→无穷;

1.2 计算控制电缆芯皮电位差的数学模型

在求解控制电缆的芯皮电位差时，可以把控制电缆数学化、模型化，可以通过π型等值电路［5］，此时控制电缆分布参数等值数学电路如图2所示。

图2 控制电缆的分布参数计算电路模型Fig.2 Calculation model of the distributed parameter control cable

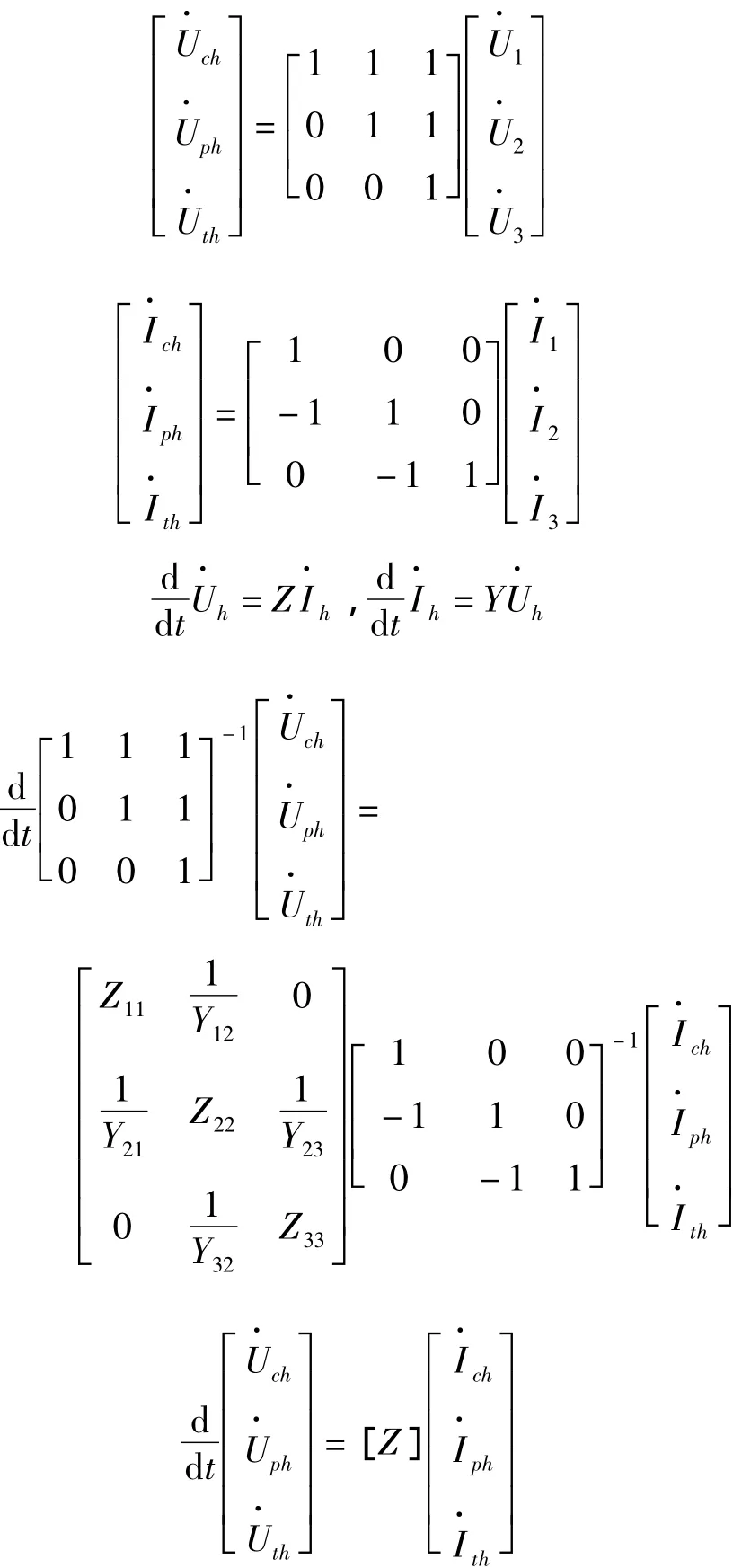
同理可得

用MATLAB编写数学模型，将所编写出的模型输入计算机，计算出各种条件下控制电缆芯线和表皮之间的电位差。

2 控制电缆不同接地方式时产生的过电压

变电站附近及内部发生雷击事故时会导致GPR升高，产生强大的电磁干扰，使控制电缆与大地之间产生过电压，易烧损控制电缆，从而危及变电站的二次设备。变电站常采用控制电缆单端接地和双端接地的方法［6］(本文仅考虑雷电作用下的暂态效应)。

2.1 控制电缆单端接地芯皮电位差的近似计算

暂态雷电流注入变电站的接地网，其最高幅值可以达到80 kA，此时在单端接地的控制电缆芯线和表皮会在强大的电磁场作用下产生电位差，如图3所示。

图3 变电站控制电缆单端接地Fig.3 Single side grounding of the substation control cable

接地导体中流过的电流为 ，oc段导体的阻抗为Z1，根据电磁感应原理［7］，雷电流在该回路产生磁通，使其感应出的电动势为∂/∂t。根据电路中的网孔电压法［7］，可以把图3近似的看成闭合的回路，进而得到控制电缆芯线和控制电缆不接地端的电势差(即图3中c，d两点之间的电势差)为

2.2 控制电缆双端接地芯皮电位差的近似计算

当控制电缆屏蔽层双端接地时，控制电缆、接地导体和接地引线三者构成闭合回路，如图4所示。

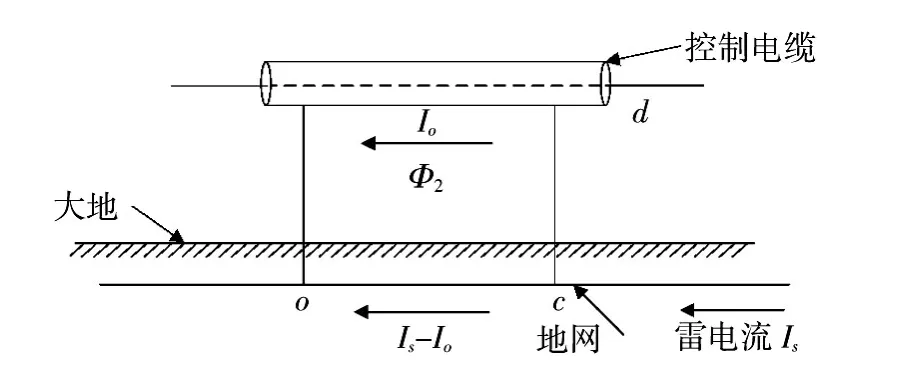
图4 变电站控制电缆双端接地Fig.4 Double side grounding of substation control cable

由支路电流法［8］可得oc段电流为，其中为雷电流为流过控制电缆屏蔽层的电流。根据网孔电流法可得

式中:Z2为接地导体oc段的阻抗;Z3为控制电缆屏蔽层的阻抗为穿过回路的磁通。

通过代数运算得

进而得出结论:变电站遭受雷击的暂态事故时，控制电缆屏蔽层采用双端接地的方式能承受更高的感应电压，有利于二次设备的保护，同时也给接地设计带来更大的裕度。

3 控制电缆芯皮电位差的影响因素

本文主要对控制电缆屏蔽层双端接地的问题进行具体测量和分析，如图5所示。点A、B、C、D、E、F为雷电流入地点，控制电缆长度为L，距离地网边缘的长度d。

图5 控制电缆及接地网布置Fig.5 Control cable and grounding network layout

影响控制电缆的芯皮电位差的因素有很多，本文主要研究接地导体不同材料、接地导体不同间距、雷电流不同注入点和大地土壤不同电阻率等因素对控制电缆芯皮电位差的影响。

3.1 接地导体材料对电缆芯皮电位差的影响

雷电流在A点注入时，接地导体材料对控制电缆芯皮电位差的影响如图6所示。

图6 接地导体材料对控制电缆芯皮电位差的影响Fig.6 Influence of ground conductor materials to potential difference of control cable core and skin

在雷电流作用下，导体间互感增大，由于钢的电阻率和磁导率比铜的大，钢材接地网的接地阻抗变得更大，因此在截面积相同条件下，钢材为接地导体时造成电缆芯皮电位差较大，且电缆越长芯皮电位差越大。

3.2 接地导体间距对控制电缆芯皮电位差的影响

雷电流在A点注入时，接地导体间距对控制电缆芯皮电位差的影响如图7所示。

图7 接地导体间距对控制电缆芯皮电位差的影响Fig.7 Influence of grounding conductor spacing to potential difference of control cable core and skin

当雷电流注入点和控制电缆长度固定时，增大接地网导体间距，雷电流作用下的暂态地网有效面积相应变小，导致接地网相邻处的地电位分布也随着变化，加大了电位的不均匀分布，从而导致控制电缆的芯皮电位差变大。

3.3 雷电流注入点对控制电缆芯皮电位差的影响

雷电流注入点对控制电缆芯皮电位差的影响如图8所示。

当固定雷电流注入点时，控制电缆在雷电流注入点一侧，控制电缆距离雷电流注入点越近，芯皮电位差越大。当注入点位于电缆中间附近时，芯皮电位差随控制电缆增长到达峰值，之后随控制电缆增长，芯皮电位差减小。

图8 雷电流注入点对控制电缆芯皮电位差的影响Fig.8 Influence of injection points of lightning to potential difference of control cable core and skin

3.4 土壤电阻率对控制电缆芯皮电位差的影响

雷电流在A点注入时，土壤电阻率对控制电缆芯皮电位差的影响如图9所示。

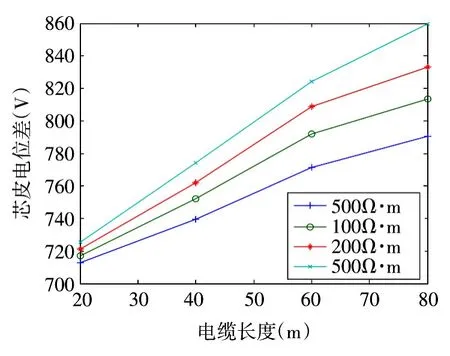
图9 土壤电阻率对控制电缆芯皮电位差的影响Fig.9 Influence of soil resistivity to potential difference of control cable core and skin difference of control cable core and skin

土壤电阻率是测量芯皮电位差的重要指标，当土壤电阻率增加时，由火花放电原理［9］知，雷电流入地点附近的接地导体等效半径增大，使雷电流主要以接地导体为通道，泄漏电流减小，接地导体的电位升高，导致控制电缆的芯皮电位差增大。

4 实例分析与实测计算

收集了某变电站实际数据。该变电站为水平三层土壤:第一层土壤电阻率ρ1=500 Ωm，高h1=3 m;第二层土壤电阻率 ρ2=300 Ωm，高 h2=5 m;第三层土壤电阻率ρ3=100 Ωm。变电站接地网面积为100×100 m2，接地导体设计距离为5、10、15和20 m，埋深1 m。接地材料为扁钢60×6 mm2(相对磁导率600、电阻率1.7×10－7Ωm)，雷电流注入点如图5中的6种情况，雷电流为2.6/50 μs，最大峰值为30 kA，控制电缆位于接地网正中间，南北方向布置。理论计算和变电站实测控制电缆芯皮电位差如表1、表2所示。

表1 本文计算控制电缆芯皮电位差Tab.1 Calculation potential difference of control cable core and skin by this paper V

表2 变电站实测控制电缆芯皮电位差Tab.2 Substation measure potential difference of control cable core and skin V

通过本文电磁场理论计算的芯皮电位差与该变电站实际测量结果进行对比，两者相差为1.3%，偏差在可接受范围内，由此可以验证本文计算方法的正确性。在暂态雷电流注入接地网时，控制电缆可以承受的最高耐受电压为2 kV。若控制电缆采用双端接地，测量出芯皮电位差最高可占GPR的40%，如表3所示。

表3 GPR与控制电缆芯皮电位差的关系Tab.3 Relationship between GPR and potential difference of control cable core and skin

从表3 可知，若 UIR＜2 kV［10］，则计算出 UGPR=5 kV时变电站各设备仍可安全运行。

5 结论

1)应用电磁场理论计算控制电缆的芯皮电位差和各个因素对芯皮电位差的影响，不仅可以快速计算出结果，而且保证了其准确性。

2)在变电站接地网设计时不仅要优化地网设计，还要考虑土壤电阻率，并合理选择接地材料，优化接地网孔大小和降低接地阻抗等。

3)控制电缆可以承受的最高耐受电压为2 kV，当暂态雷电流注入地网时，控制电缆采用屏蔽层双端接地的方式，可将GPR的限值提高到5 kV，仍可保持控制电缆和二次设备安全运行。

［1］ 郭剑，邹军，何金良，等.水平分层土壤中点电流源格林函数的地推算法［J］.中国电机工程学报，2004，24(7):101 －105.GUO Jian，ZOU Jun，HE Jinliang，et al.Recursive method to obtain analytic expressions of Green’s functions in multi－ layer soil by computer［J］.Proceedings of the CSEE，2004，24(7):101 －105.

［2］ RUSCK S.Induced lightning over－voltages power transmission lines with specialreference to the overvoltage protection of low－voltage networks［D］.Stockholm:Royal Institute of Technology，1957.

［3］ 惠梅，王东生，李庆祥，等.基于离散泊松方程解的相位展开方法［J］.光化学报，2003，23(10):1245 －1249.HUI Mei，WANG Dongsheng，LI Qingxiang，et al.Phase unwrapping method based on the solution of discrete passion equation［J］.Acta Optica Sinica，2003，23(10):1245 －1249.

［4］ 张健.数学物理方程的分离变量法［J］.青海师范大学学报:自然科学版，2007(3):17－19.ZHANG Jian.Method of separation of variables in mathematical equations of physics［J］.Journal of Qinghai Normal University，2007(3):17－19.

［5］ 宫杨非，衣涛，桂萍，等.基于π型等值模型的线路参数计算和估计方法［J］.华东电力，2012，40(4):586 －589.GONG Yangfei，YI Tao，GUI Ping，et al.Line parameter calculation and estimation method based on π－type equivalent model［J］.East China Electric Power，2012，40(4):586 －589.

［6］ THOMAS D E，WIGGINS C M.Induced transients in substation cables:Measurements and Models［J］.IEEE Transactions on Power Delivery，1994，9(4):1861 －1868.

［7］ 曾令全.电机学［M］.北京:中国电力出版社，2007.ZENG Lingquan.Electromechanics［M］.Beijing:China Electric Power Press，2007.

［8］ 刘耀年，霍龙.电路［M］.北京:中国电力出版社，2005.LIU Yaonian，HUO Long.Circuit［M］.Beijing:China Electric Power Press，2005.

［9］ 杨琳，吴广宁，曹晓斌，等.接地导体雷电暂态响应建模分析［J］.中国电机工程学报，2011，31(13):142 －146.YANG Lin，WU Guangning，CAO Xiaobin，et al.Modeling of grounding electrode for lightning transient response analysis［J］.Proceedings of the CSEE，2011，31(13):142 －146.

［10］ 鲁志伟，马文婧，宋文国，等.新立变电站接地系统安全性能研究［J］.东北电力大学学报，2012，32(6):28 －32.LU Zhiwei，MA Wenjing，SONG Wenguo，et al.Study on the safety performance of grounding system of the substation［J］.Journal of Northeast Dianli University，2012，32(6):28 －32.