用度量误差模型方法建立油松树高曲线方程组1)
蒋益 邓华锋 高东启 夏朝宗
(北京林业大学,北京,100083) (国家林业调查规划设计院)
责任编辑:王广建。
度量误差模型在林业上的应用已引起人们越来越多的重视,研究也越来越深入。唐守正等[1]讨论了度量误差模型在生物学中应用的可能性,认为在研究群体不同性状之间的数量关系时,度量误差模型往往比通常回归模型接近实际。度量误差模型估计方法优于普通回归估计方法[1-5],使用度量误差模型方法进行估计效果更好。
树高和胸径是衡量林分生长标准的两个重要的指标。外业调查中实测树高比较困难,且工作量大,而建立合理的树高曲线方程则能有效的预测林分的树高。但在实际的林业调查中,胸径的观测值往往含有各种不同的误差。树高、胸径、林龄三者之间都存在着密切的相关关系[6-11],如果只单纯考虑树高与胸径关系,而不考虑树高、胸径与林龄的关系,会导致各因子之间不相容,也可能使预测的结果不一致。本文以黄土高原的油松(Pinus tabulaeformis)天然林为例,利用度量误差模型的方法,建立林分相容性树高曲线方程组,使树高、胸径、林龄3个因子相互预测时保持相容性和一致性,并对油松林分的生长情况进行分析。
1 研究地概况
研究地为黄土高原中心地带的子午岭和黄龙山,地理坐标介于东经116°40'10″~112°22'10″,北纬34°33'29″~39°35″08″。地貌以黄土丘陵沟壑为主,东部吕梁山有部分土石山地,海拔800~1 500 m。气候属暖温带大陆性季风气候,四季分明,冬季寒冷少雪,春季干燥多风,夏季炎热多雨,秋季温凉湿润。年平均气温10℃,≥10℃积温2 800~3 900℃,无霜期120~170 d。年降水量400~640 mm。主要土壤类型为褐土。属暖温带落叶阔叶林地带,主要树种有:辽东栎(Quercus liaotungensis)、麻栎(Quercus acutissima)、白桦(Betula platyphylla Suk)、青杄(Picea wilsonii Mast)、山杨(Populus davidiana)、油松、侧柏(Platycladus orientalis)等。
2 研究方法
2.1 样地调查及数据整理
本次研究所采用的数据为第七次、第八次一类清查数据,每个样地的面积为0.066 7 hm2。样地调查因子有:林木胸径、林龄、林分平均高、林分蓄积、郁闭度、水平距、坡向、坡位、坡度、海拔高度、土层厚度等,样地固定,每隔5年复测一次。从数据库中挑选油松天然林样地,除去记录不详、离散异常的样地,最终剩余油松天然林样地119块,其中90块用于建模,29块用于检验。样地基本情况如表1所示。

表1 样地基本情况
2.2 胸径生长曲线和树高曲线方程
用来模拟林分生长过程曲线的方程很多,有Richards方程、Wykoff方程、Korf方程、Logistic方程、幂函数方程、Bates方程、单分子型方程、抛物线方程等[13-15]。采用Richards方程,确定林分胸径生长过程曲线方程和树高生长曲线方程:

式中:D为胸径;H为树高;T为林龄;a、b、c为参数。
2.3 非线性度量误差联立方程组
通常的回归模型,是假定自变量的观测值不含误差,而因变量的观测值含有误差。误差可能有各种来源,如抽样误差、测量误差等,一般统称为度量误差。当自变量和因变量的观测值中都含有度量误差时,通常的回归模型估计方法就不再适用,而必需采用误差变量模型方法[17-19];当涉及到多个方程的联合估计时,则必需采用误差变量联立方程组[17-20]。
多元非线性误差变量联立方程组(也称非线性度量误差模型)的向量形式为[16]:
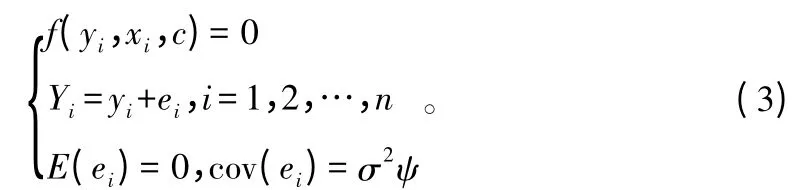
其中,xi是q维无误差变量的观测数据,yi是p维误差变量的观测数据,f是m维向量函数,Yi是yi的未知真值,误差的协方差矩阵记为Φ=σ2ψ,ψ是ei的误差结构矩阵,σ2为估计误差。
在油松林分中,胸径(D)、树高(H)、林龄(T)三者之间的相关关系中,H-D、D-T这两个相关关系中包含着一个H-T的关系。胸径生长过程曲线方程(D-T)给出了T→E(D|T)的关系,树高曲线方程给出了D→E(H|D)的关系。树高生长过程曲线方程(H-T)给出了T→E(H|T)的关系。考虑T→E(H|T)和T→E(H|E(D|T))的相容性,可采用误差变量联立方程组[16-19]。由公式(1)和(2)构成了非线性度量误差联立方程组(4),把公式(4)称为树高曲线联立方程组。在公式(4)中,胸径(D)由单木胸径推算而来,树高是估测得到的,因此将H、D作为误差变量,T作为无误差变量。

对于公式(4),采用非线性度量误差模型方法来求解各个参数,从而保证了树高曲线方程、胸径生长过程曲线方程和树高生长过程曲线方程三者之间的相容性和一致性。
利用度量误差模型(相容性模型)建立的联立方程的效率,当通过T、D、H三个变量中的一个变量预测其它两个变量时,其结果与其他两个变量相互预测的结果是一致的。当林龄(T)确定时,其对应的胸径(D)与树高(H)也是确定的,而且这个预测结果与树高曲线(H-D)直接预测的结果是一致的。而传统的树高曲线、树高生长方程、胸径生长方程的单独预测模型,不能使这3个变量相互预测时保持一致。
2.4 参数估计与模型检验
综合应用ForStat、Excel进行数据处理和参数估计,设定误差的协方差矩阵为UI基本型,统计参数的估计值和相关系数。对所拟合的方程进行t检验,并计算平均绝对偏差(MAD)、均方根误差(RMSE)和预估精度(P)等几个指标来检验模型的预测能力,它们的数学表达式如下:
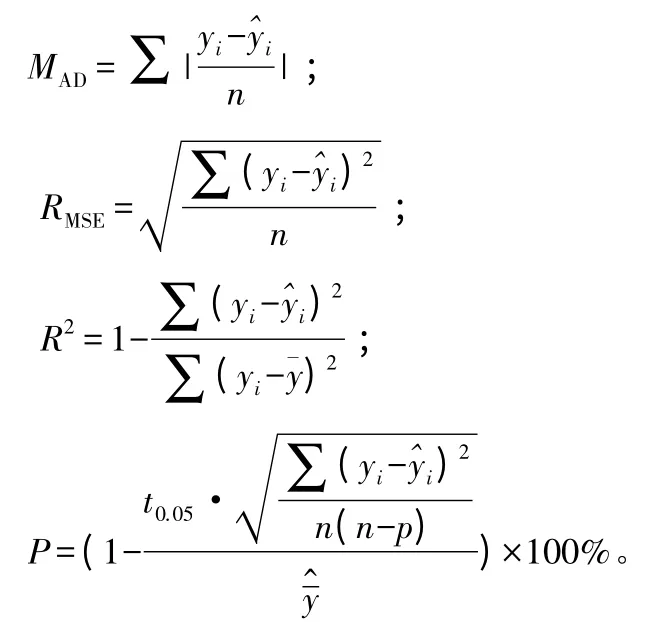
式中:yi为实测值为模型预估值为模型预估值的平均值,n为样本数,p为模型参数个数,t0.05为置信水平a=0.05时的t分布值。
3 结果与分析
使用ForStat软件中的非线性度量误差联立方程组求解,得到油松树高曲线、胸径生长过程曲线方程的参数,并计算各个方程的平均绝对偏差(MAD)、均方根误差(RMSE)和预估精度(P),统计相关结果见表2、表3。由表3可知,油松树高曲线拟合的决定系数为0.413 3,平均绝对偏差(MAD)1.630 1、均方根误差(RMSE)2.087 7,预估精度为96.12%。胸径生长过程曲线拟合的确定系数为0.702 7,平均绝对偏差(MAD)为2.225 6、均方根误差(RMSE)为2.699 9,预估精度为96.53%。经检验,树高曲线的决定系数为0.463 1,平均绝对偏差(MAD)1.432 2、均方根误差(RMSE)1.775 2,预估精度为93.22%。胸径生长过程曲线拟合的确定系数为0.694 8,平均绝对偏差(MAD)为1.894 7、均方根误差(RMSE)为2.088 1,预估精度为94.03%。说明所建立的树高曲线联立方程组比较合理,对油松林分的树高、胸径的生长预测较为准确。

表2 树高曲线联立方程组参数统计

表3 树高曲线联立方程组检验指标统计
分别绘制油松的胸径生长过程曲线和树高曲线,结果如图1、图2所示。

图1 油松胸径生长过程曲线

图2 油松树高曲线
从图1、图2可知,平均油松林分的树高4~18 m,胸径5~28 cm,平均林龄在20~95 a,而油松天然林在60 a时达到成熟龄,31~50 a为中林龄,说明晋陕黄土高原油松天然林的龄组结构比较均衡;随着林分林龄的增长,林分平均胸径的生长速度在20~40 a较快,此后胸径的生长速度逐渐趋于缓慢;而树高随林分平均胸径的生长变化而变化,平均胸径为5~10 cm时树高生长最快,此后逐渐减小。
根据所建立的树高曲线联立方程组H-D、D-T的相关关系可推导出H-T的关系,油松林分树高生长过程曲线如图3所示。

图3 油松树高生长过程曲线
由图1、图3中可知,随着林分林龄的增长,油松林分的树高生长极盛期为20~30 a,此后树高生长速度变缓。林分胸径生长极盛期为30~40 a,这说明随着油松林龄的增长,胸径生长的速生期要滞后于树高生长的速生期,树高生长极盛期大约在20~30 a,胸径的生长极盛期大约出现在树高生长极盛期之后。
4 结论与讨论
利用一类清查数据,基于Richards方程采用度量误差模型方法,建立了晋陕黄土高原油松天然林的树高曲线联立方程组,经检验,预测效果较好,对油松林分的树高、胸径的预估精度都达到95%以上。随着油松林分林龄的增长,胸径生长的速生期要滞后于树高生长的速生期,树高生长极盛期出现在林龄20~30 a,胸径生长极盛期出现在林龄30~40 a。
所建立的树高曲线联立方程组中,隐含着树高生长过程曲线方程,使得林分的胸径、树高生长过程曲线与树高曲线之间具有相容性和一致性,即运用树高曲线、树高生长过程曲线分别预测林分高度的结果是一致的;同时,还考虑了树高、胸径、林龄3个变量的度量误差;采用度量误差模型的方法建模能优化模型结构,可以减小外业调查的测量误差对预测结果的影响,使模型具有较强的生物学意义和解释性。树高曲线联立方程组尝试了从林分水平对树高曲线进行研究,从而为从林分水平预测油松树高的整体生长状况提供了参考和依据。
[1]唐守正,张淑梅.度量误差模型及其应用[J].生物数学学报,1998,13(2):161-166.
[2]李永慈,唐守正,徐松.线性度量误差模型的参数估计法与最小二乘法的关系[J].生物数学学报,2008,23(1):139-142.
[3]李永慈,唐守正,李海奎.用两阶段度量误差模型方法和ForStat软件进行模型整合[J].林业科学,2004,40(2):75-78.
[4]吴明山,胥辉.度量误差对材积模型的影响及参数估计研究[J].北京林业大学学报,2008,30(5):83-86.
[5]李永慈,唐守正.带度量误差的全林整体模型参数估计研究[J].北京林业大学学报,2006,28(1):23-27.
[6]胡云云,亢新刚,赵俊卉.长白山地区天然林林木林龄与胸径的变动关系[J].东北林业大学学报,2009,37(11):38-42.
[7]吴树朗.云龙县云南松林林龄、直径、树高关系分析[J].云南林业调查规划,1991(2):25-27.
[8]彭鸿,S.Bernd.渭北黄土高原油松人工林生长过程及其与立地和人为干扰的关系[J].陕西林业科技,2003(1):1-6.
[9]李春明,李利学.基于非线性混合模型的栓皮栎树高与胸径关系研究[J].北京林业大学学报,2009,31(4):7-12.
[10]柳明来,张芬玲.黄龙山林区主要树种的树高与胸径关系的分析[J].陕西林业科技,2002(02):44-48.
[11]刘金福,洪伟.格氏栲种群个体林龄与胸径的时间序列模型研究[J].植物生态学报,1999,23(3):283-288.
[12]樊艳文,王襄平,曾令兵,等.北京栓皮栎林胸径:树高相关生长关系的分析[J].北京林业大学学报,2011,33(6):146-150.
[13]曾翀,雷相东,刘宪钊,等.落叶松云冷杉林单木树高曲线的研究[J].林业科学研究,2009,22(2):182-189.
[14]赵俊卉,亢新刚,张慧东,等.长白山3个主要针叶树种的标准树高曲线[J].林业科学,2010,46(10):191-194.
[15]陈立莉.树种树高曲线模型的研究[D].哈尔滨:东北林业大学,2013.
[16]唐守正,郎奎建,李海奎.统计与生物数学模型计算(ForStat教程)[M].北京:科学出版社,2009.
[17]李永慈,唐守正,李海奎,等.用度量误差模型方法编制相容的生长过程表和材积表[J].生物数学学报,2004,19(2):199-204.
[18]曾伟生,唐守正.利用度量误差模型方法建立相容性立木生物量方程系统[J].林业科学研究,2010,23(6):797-803.
[19]曾伟生,夏忠胜,朱松,等.贵州人工杉木相容性立木材积和地上生物量方程的建立[J].北京林业大学学报,2011,33(4):1-6.
[20]党永峰,王雪军,曾伟生.用分段建模方法建立东北落叶松立木材积和生物量方程[J].林业科学研究,2012,25(5):558-563.

