组合型交叉熵算法在电网故障诊断中的应用

边 莉，边晨源，田志龙

（黑龙江科技大学电子与信息工程学院，哈尔滨150027）

由于电网规模的扩大、设备的增多，故障诊断的难度逐渐加大。电网故障诊断方法主要有专家系统[1-2]，人工神经网络[3-5]，Petri 网[6-8]和优化技术[9-11]等。专家系统是将专家的知识应用于故障诊断，保证了诊断系统的实时性和有效性，但知识库的建立较困难，系统维护难度大；神经网络具有强大的学习能力，容错能力强，但系统训练需要大量的样本，建立完备的样本集十分困难；Petri 网是对电网故障这种离散事件进行动态建模和分析的有效方法，具有图形化的结构表示等优点，但当电网发生多重故障时，Petri 网诊断结果不够理想；优化技术通过对故障问题进行解析化建模，将故障诊断问题转变为使目标函数最小化的0-1 整数规划问题，采用优化算法求解这一问题，具有严密的数学基础和理论依据。目前，优化算法主要包括粒子群算法、遗传算法、模拟退火算法和禁忌搜索算法等。文献[9]建立表征电网故障的0-1 整数规划模型，分别采用遗传算法和模拟退火算法求解目标函数最优解，验证了这两种算法在实现电网故障诊断上的有效性；文献[10]采用禁忌搜索算法来求解同一优化问题；文献[11]给出了一种电网故障的完全解析模型，并利用离散型粒子群算法优化目标函数，最终识别故障元件。

交叉熵CE（cross entropy）算法是一种全局随机优化算法，利用参数化的概率密度分布产生随机样本，使每次迭代使用的候选样本都发生变化，因此优化过程不易陷入局部最优解[12]。该算法已被用于解决大型、复杂的优化问题。但目前，国内外专家学者鲜有将该算法应用于电网故障诊断。

本文在前人研究的基础上，结合CE 理论，将CE 算法中的组合型交叉熵CCE（combinatorial CE）算法引入电网故障诊断领域。把电网故障诊断问题归结为0-1 整数规划问题，利用该算法求解故障诊断模型的最优解，成功识别故障元件。应用本文方法对测试系统中的多种典型故障情况[9，16]进行测试，其中，故障情况包括保护器和断路器拒动及多重故障等复杂情况，最终诊断结论全部正确。将本文方法同粒子群算法和遗传算法比较，证明了本文方法具有高稳定性、收敛速度更快等优点。

1 电网故障诊断问题的模型

电网的故障诊断可以表述为最小值的问题，即

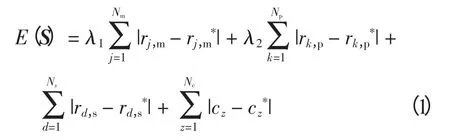
式中：S=[S1，S2，…，SN]是目标函数的自变量，它是一个N 维向量，用来表示诊断系统中元件的状态，其中Si（i = 1，2，…，N）表示第i 个元件的状态，Si只取0 或1，表示该元件是正常或故障状态；N 为诊断系统中所包括的元件总个数；Nm、Np、Ns、Nc分别表示系统中主保护、近后备保护、远后备保护和断路器的数量；rj，m、rj，m*分别表示第j 个主保护的实际和期望状态，rj，m=0 或1 表示第j 个主保护未动作或动作，其中rj，m*=0 或1 分别表示主保护不应该动作或应该动作；rk，p、rk，p*为第k 个近后备保护的实际和期望状态；rd，s、rd，s*表示第d 个远后备的实际和期望状态；cz、cz*表示第z 个断路器的实际和期望状态；λ1，λ2为权重因子，取值为正实数，引入权重因子是为了消除主保护和近后备保护拒动时对目标函数产生的影响。其中λ1=|1-rk，prk，p*-为0 时，结果为1）。显然主保护拒动，后备保护动作时，由于|rj，m-rj，m*|=1，目标函数值将增大，此时λ1=0，因此乘以λ1能够消除此影响。同理，为了消除近后备保护拒动，而由远后备保护动作切断故障时对目标函数的影响，近后备部分需要乘以λ2=原则在文献[10]中有详细介绍。

电网故障诊断就是应用优化算法找到使E（S）取得最小值的S=[S1，S2，…，SN]，由于Si（i=1，…，N）的取值只为0 或1。从而该诊断问题是一个典型的0-1 整数规划问题。

2 CE 算法

CE 算法是Rubinstein 在1997 年根据现代信息论中的Kullback-Leibler 距离（也叫交叉熵）概念提出的一种用于模拟小概率事件发生的自适应算法[13]。结合重点采样策略，使该算法可以更好的估算小概率事件的发生。

通常情况下，CE 算法包含一个迭代的过程，每次迭代能够拆分为两个步骤。

（1）基于某一特定的概率密度函数，产生一组随机数据样本。

（2）依据这些数据样本更新概率密度函数的参数，从而为下次迭代贡献更优化的样本。

在优化过程中，CE 算法的操作是基于参数化概率密度分布，每次迭代使用的候选样本都发生变化，这是CE 算法的基本特性[12]。

2.1 CCE 算法主要思想

考虑以下的求解最小值问题，χ 是一个表示状态的有限集，G 是以χ 为定义域的实值函数，其中γ*为G 的最小值，x*为最优解，因此该组合优化问题可以描述成为

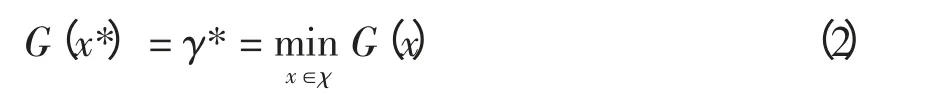
设在χ 上的一个概率密度函数族为{f（·；v），v∈V}。对于一个给定的概率密度f（·；u），u∈V，将式（2）的优化问题与式（3）的估计问题进行关联，研究G（x）比给定实数γ 小的概率问题。

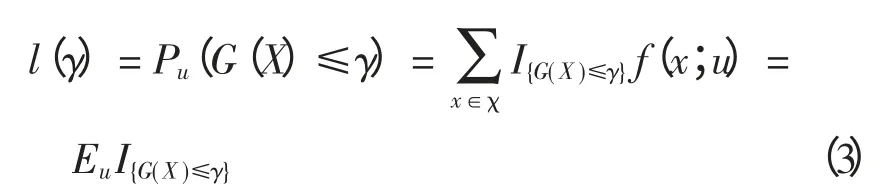
式中：{I{G(X)≤γ}}表示指示函数集合，X 是依据概率密度f（·；u）产生的随机样本；Eu表示相应的期望值。当γ 逐渐接近γ*时，所选定的u 要保证Pu（G（X）≤γ）的值不是太小，这样才有实际意义[18]。因此式（3）中γ 和u 的选取是紧密相关的。为了克服上述问题，可以采用多级别算法，其思想是构造参考参数序列{vt，t ≥0}和级别序列{γt，t ≥1}，然后vt和γt同时更新迭代。其中γt的更新值为在给定参数vt-1下G（X）的（1-ρ）分位点，ρ 不可太小。直到某次迭代后参考参数序列vt中对应元素改变量的最大值小于某一规定参数bm时，迭代结束。

2.2 CCE 算法流程

由电网故障诊断问题的目标函数E（S）可知，S ={S1，S2，…，SN}中的元素Si（i = 1，2，…，N）是一个定义域为0 和1 的量，显然Si取值服从1 重Bernoulli 分布（也称0-1 分布），因此CCE 算法中的概率密度函数选择为Bernoulli 分布。设试验成功概率为p，则概率密度为

当x=1 时，f（x；p）=p

当x=0 时，f（x；p）=1-p

结合CCE 算法主要思想，得到以下算法流程：

（1）开始：设置参数，初始化参数向量p0，随机样本个数M，分位数系数ρ、bm，平滑常数β、n（p0的维数），令迭代次数t=0。

（2）取样：令t = t + 1，根据参数为p（t-1）的Bernoulli 分布产生M 个随机样本X=[X1，…，XM]T，且每个随机样本Xa（1〈a〈M）都是n 维向量，其中Xa=（xa1，…，xan）。

（3）排序：计算目标函数序列E=[E1，E2，…，EM]T，并将该序列中的元素从小到大排列得到新的矩阵序列按照式（5）计算序列的（1-ρ）分位数。

（4）更新：利用产生的M 个随机样本代入式（6），更新参数p=（p1，p2，…，pn）

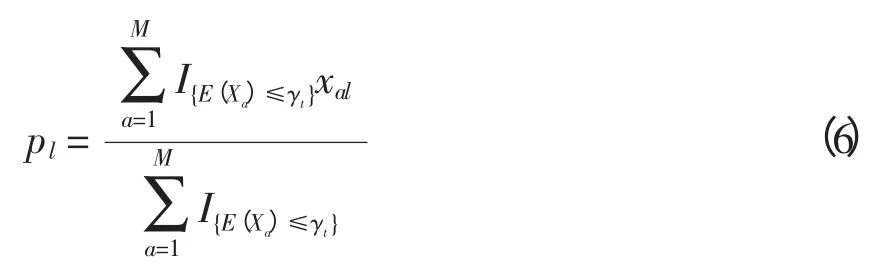
式中，l=1，…，n。

（5）平滑：

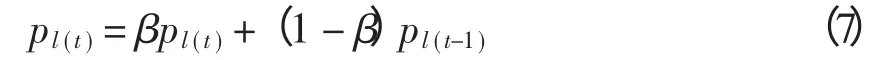
式中：0.5 ≤β ≤0.9；pl(t)为第t 次迭代后参数序列中的第l 个元素，l=1，…，n。

（6）停止：判断停止条件，如果相邻两次迭代产生的参数序列中的各个元素满足max（|pl(t)-pl(t-1)|）〈bm（l=1，…，n）条件，迭代结束。否则重新执行步骤（2）～（6）。

程序执行过程中，CCE 算法会产生参数序列{pl，t ≥0}和分位数序列{γl，t ≥1}。根据Bernoulli分布的特点，算法终止时，参数序列为最优解，分位数序列为最优值。

3 算法测试与分析

对图1 所示的典型测试系统进行分析。系统中共有28 个元件，40 个断路器以及84 个保护，其中主保护36 个，后备保护48 个。

（1）28 个元件为：母线A1，…，A4，B1，…，B8，变压器T1，…，T8，输电线路L1，…，L8。

（2）40 个断路器为：CB1，CB2，…，CB40。

（3）在84 个保护中，有36 个主保护：母线A主保护A1m，…，A4m，母线B 主保护B1m，…，B8m，变压器主保护T1m，…，T8m，输电线路主保护L1Hm，L1Rm，…，L8Hm，L8Rm（H 和R 定义为线路的首末端或上下端）；24 个近后备保护：变压器近后备T1p，…，T8p，输电线路近后备L1Hp，L1Rp，…，L8Hp，L8Rp。24 个远后备保护：变压器远后备T1s，…，T8s，输电线路远后备L1Hs，L1Rs，…，L8Hs，L8Rs。

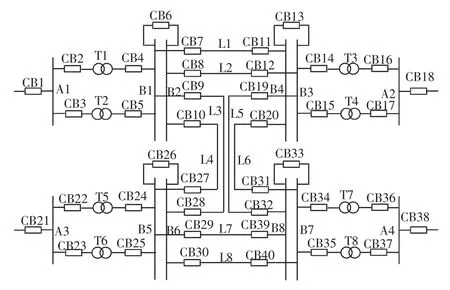
图1 测试系统Fig.1 Test system

3.1 故障区域识别

电网故障后，为了防止故障区域扩大，相关保护和断路器会动作切除故障区域（也称停电区域），使该区域孤立在电网中，而且故障元件一定被限制在该区域内。电网故障诊断过程可以只针对停电区域进行，极大地减小诊断难度[15]。

3.2 报警信息分析

输电线路L1、L2 和母线B1、B2 同时发生故障时，保护器和断路器动作信息如下。

母线主保护B1m、B2m 动作，断路器CB4、CB5、CB6、CB7、CB8、CB9、CB10 跳闸。输电线路主保护L1Hm 动作，L1Rm 拒动，近后备保护L1Rp 动作，断路器CB7、CB11 跳闸。L2Rm 正确动作，L2Hm 拒动，近后备保护L2Hp 动作，跳开断路器CB12、CB8。

调 度 中 心 接 收 到B1m，B2m，L1Hm，L2Rm，L1Rp，L2Hp，CB4，CB5，CB6，CB7，CB8，CB9，CB10，CB11，CB12 动作的报警信息。

故障诊断过程中，所需变量可如下选定：

（1）在停电区域内的可疑元件选定为B1、B2、L1、L2 这4 个电网元件，对应于S=[S1，S2，S3，S4]。

（2）选定9 个断路器为：CB4、CB5、CB6、CB7、CB8、CB9、CB10、CB11、CB12，状态对应于c=[c1，c2，c3，…，c9]。

（3）选定的保护有14 个，其中6 个主保护B1m、B2m、L1Hm、L1Rm、L2Hm、L2Rm，4 个近后备保 护L1Hp、L1Rp、L2Hp、L2Rp，4 个远后备保护L1Hs、L1Rs、L2Hs、L2Rs，对应状态r=[r1，r2，…，r14]。

根据调度中心接受到的报警信息，确定

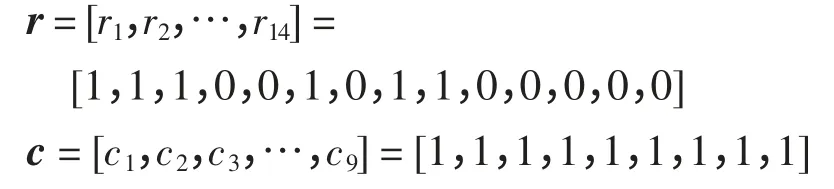
3.3 算法测试

根据式（1）可知，上述测试系统的故障诊断模型的目标函数为

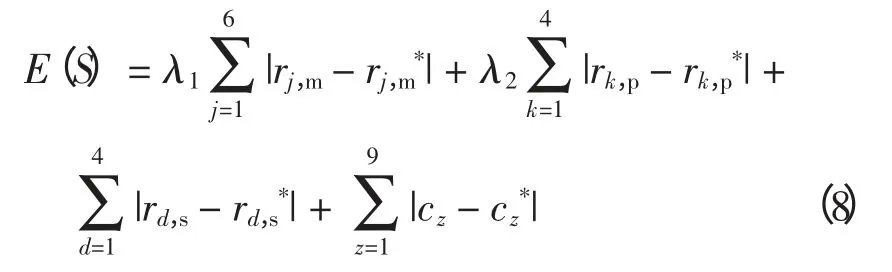
将保护器和断路器的期望状态r*和c*的值，连同报警信息代入式（8），具体目标函数为

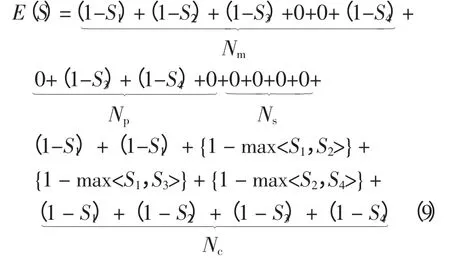
经化简后得到，

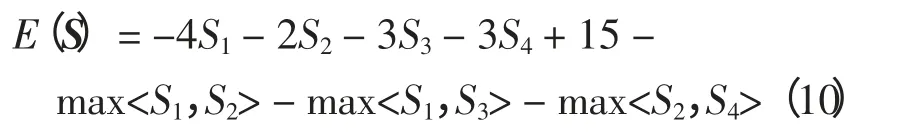
利用CCE 算法优化式（10），选取初始化分位数系数ρ 为0.7，随机样本个数M = 30，平滑系数β = 0.9，输入n = 4 维的初始参数向量p =[0.5，0.5，0.5，0.5]，计算精度bm选择1×10-4。

程序连续运行30 次，计算结果平均在迭代7次前收敛。随机选取某次计算过程，结果如图2 所示。

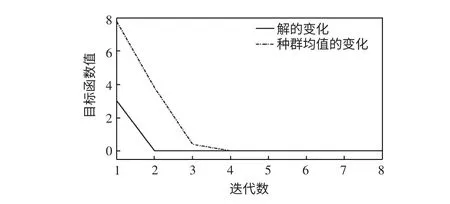
图2 CCE 算法最优解和种群均值的变化Fig.2 Optimal solution and population mean of CCE algorithm

CCE 算法在第2 次迭代时，已经搜索到目标函数最优值，种群均值在迭代6 次之前就趋于稳定。得到E（S）最优值为0，对应的最优解为S =[1，1，1，1]。在本次计算过程中γt和pt序列的分布情况如表1 所示，展示了CCE 算法程序在执行时，每次迭代概率p 向目标概率p*逼近的收敛趋势。当p 的分量全部变为1 且恒定时，表明CCE 算法已得到目标函数E（S）的最优解。

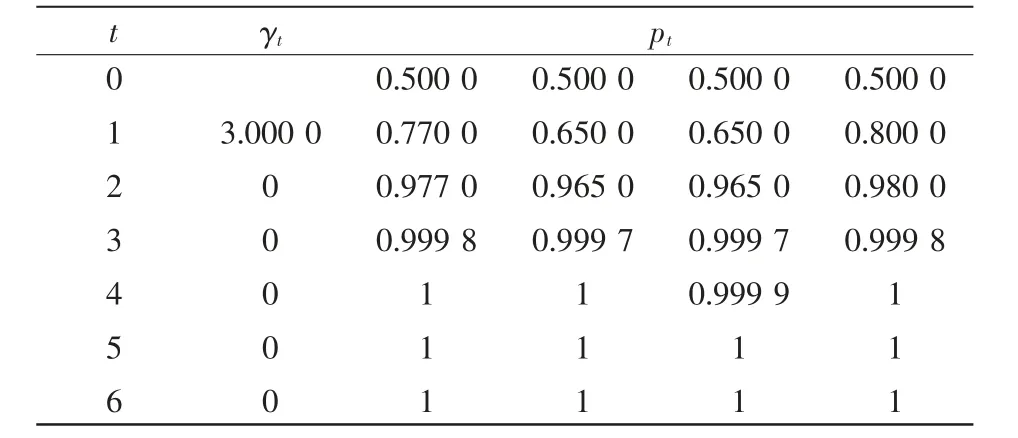
表1 参数向量分布情况Tab.1 Convergence of the parameter vector

图3 为迭代过程中，种群每个个体取得的目标函数值的变化情况，可以看出在迭代6 次之前，种群中每个粒子都搜索到了各自的最优解，并且取值趋于稳定。

用粒子群算法求解上述问题，粒子维数设为4，粒子数目为30，学习因子C1=0.7，C2=0.7，惯性权重值W=0.8，最大迭代次数为50。计算结果如图4 所示。

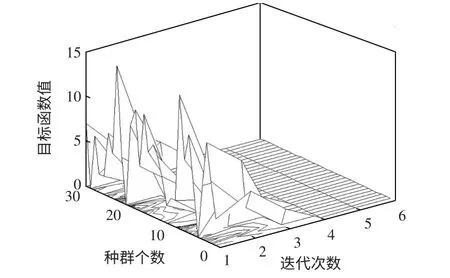
图3 CCE 算法每代种群中每个个体的目标函数值Fig.3 Unit objective function values of all generations of CCE algorithm

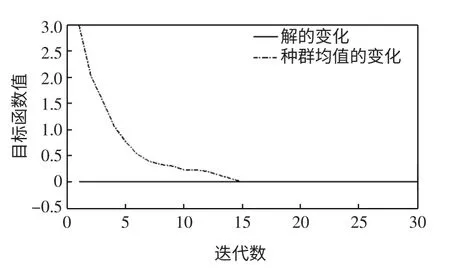
图4 粒子算法得到的最优解和种群均值的变化Fig.4 Optimal solution and population mean of PSO

虽然粒子群算法在第1 代时就已经搜索到最优值，但是种群均值在15 代以后才趋于稳定。可见粒子群算法比CCE 算法所需迭代次数多，收敛速度慢。图5 能够看出种群中每个粒子搜索到稳定的最优解所需的迭代次数要大于CCE 算法。

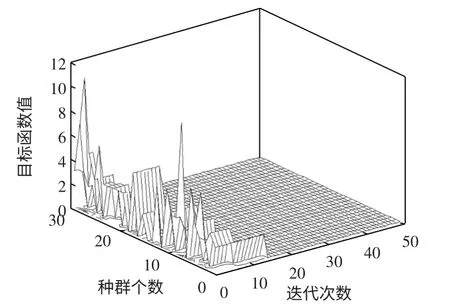
图5 粒子群算法每代种群中每个个体目标函数值Fig.5 Unit objective function values of all generations of PSO

遗传算法常用来求最大值，目标函数变为如式（11）所示求最大值的问题。U 为较大的正实数，用来保证D（S）恒为正，本文取U=50，种群数设为30，最大迭代次数为100，杂交概率Pc= 0.9，变异概率Pm=0.04，诊断结果如图6 所示。

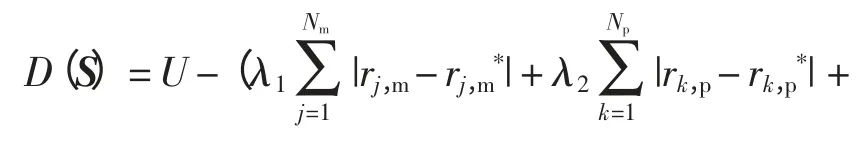
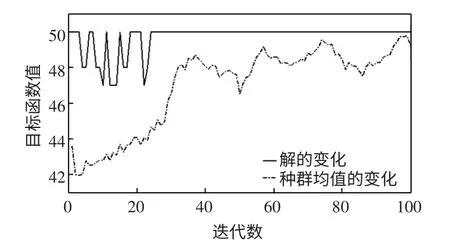
图6 遗传算法得到的最优解和种群均值的变化Fig.6 Optimal solution and population mean of GA

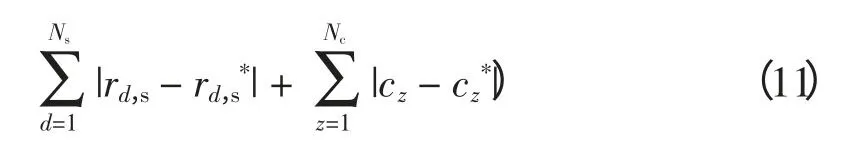
图中可以看出，遗传算法虽然较早搜索到最优值，但值不稳定，种群均值变化大。同时应用遗传算法的故障诊断会得到多种计算结果，诊断结果不唯一，导致诊断结论不精确。图7 可以看到每代种群中个体取值的分散性。

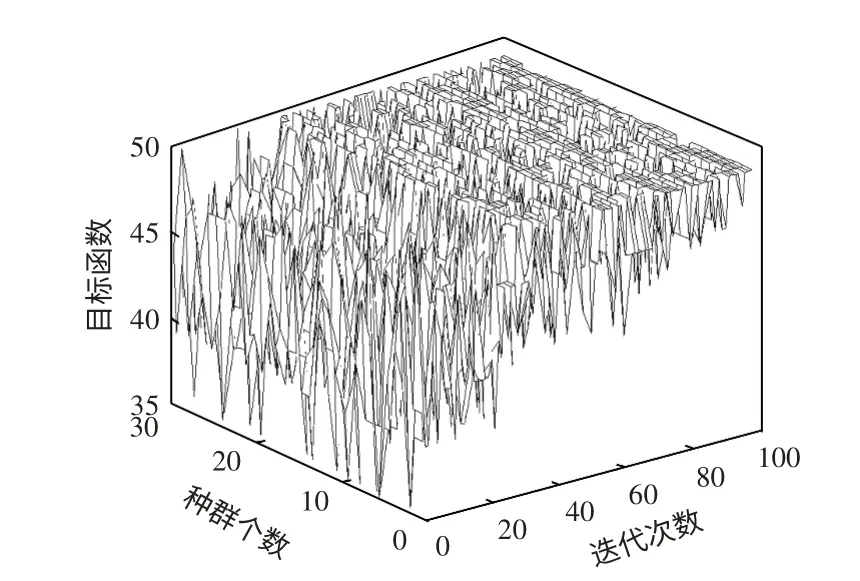
图7 遗传算法每代种群中每个个体的目标函数值Fig.7 Unit objective function values of all generations of GA

连续进行30 次仿真测试，都得到类似上述结果。3 种算法比较可知：CCE 算法所需的迭代次数要小于其他两种算法；同时粒子群算法每次迭代过程不仅要更新每个粒子速度和位置，还要评价每个粒子的适应值，以寻找全局最优；遗传算法的迭代过程具有交叉和变异环节，易产生冗余迭代，计算过程同样复杂；而CCE 算法基于参数化的概率密度产生随机样本，每次迭代只需更新概率密度参数和分位数，因此相比于其他两种算法，CCE算法需要更短的处理时间。在稳定性上也优于其他两种算法。更加满足电网故障诊断对实时性的要求。

上述故障诊断结果表明：测试系统故障元件为B1、B2、L1、L2，诊断结论正确。为了进一步说明本文算法的有效性，对图1 测试系统中的多种典型故障情况[9，16]进行测试分析，其中，故障情况包括保护器和断路器拒动及多重故障等复杂情况，诊断结果见表2。

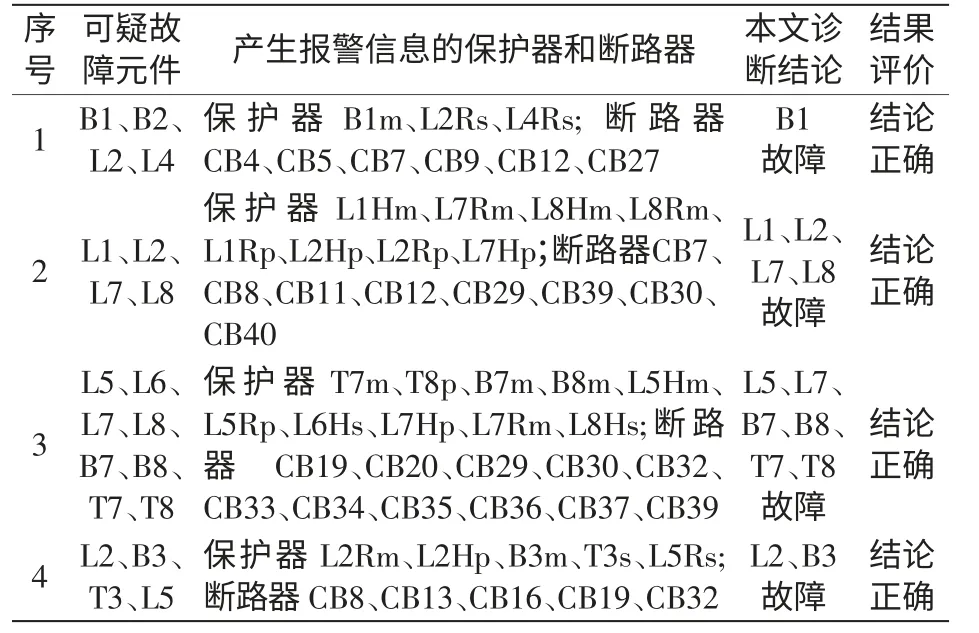
表2 故障诊断结果Tab.2 Results of fault diagnosis

4 结语

本文利用CCE 算法来解决电网故障诊断问题。通过选取多个故障实例来验证该方法的有效性。其中包含保护器或断路器拒动以及多重故障等复杂情况，利用本文的诊断方法，均能得到正确的诊断结果，而且诊断速度快、精度高。同时基于CCE 算法的电网故障诊断方法较目前常用的优化算法，过程更加简洁，可维护性高，具有更快的收敛速度和更高的稳定性。

基于CCE 算法的电网故障诊断方法作为一种新的应用，具有较为广阔的应用前景，可以考虑将其应用到电网的在线故障诊断等诸多方面。下一阶段的研究重点在于如何提升算法的容错性和适应性等方面。

[1]Lee HeungJae，Park DeungYong，Ahn BokShin，et al. A fuzzy expert system for the integrated fault diagnosis[J].IEEE Trans on Power Delivery，2000，15（2）：833-838.

[2]赵伟，白晓民，丁剑，等（Zhao Wei，Bai Xiaomin，Ding Jian，et al）. 基于协同式专家系统及多智能体技术的电网故障诊断方法（A new fault diagnosis approach of power grid based on cooperative expert system and multi-agent technology）[J]. 中国电机工程学报（Proceedings of the CSEE），2006，26（20）：1-8.

[3]毕天姝，倪以信，吴复立，等（Bi Tianshu，Ni Yixin，Wu Fuli，et al）.基于新型神经网络的电网故障诊断方法（A novel neural network approach for fault section estimation）[J].中国电机工程学报（Proceedings of the CSEE），2002，22（2）：73-78.

[4]罗毅，程宏波，吴浩，等（Luo Yi，Cheng Hongbo，Wu Hao，et al）. 一种基于小波分时灰度矩与概率神经网络的电网故障诊断方法（A novel method of power system′s fault diagnosis based on wavelet time-division gray moment and probability neural network）[J]. 重庆邮电大学学报：自然科学版（Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition），2012，24（1）：121-126.

[5]Khomfoi S，Tolbert L M.Fault diagnosis system for a multilevel inverter using a principal component neural network[C]//37th IEEE Power Electronics Specialists Conference.Jeju，South Korea，2006.

[6]刘思化，李霞（Liu Sihua，Li Xia）.谓词Petri 网理论在电网故障诊断中的应用（Power system fault diagnosis by use of predicate Petri net models）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（4）：162-166.

[7]林振智，文福拴，钟志勇，等（Lin Zhenzhi，Wen Fushuan，Zhong Zhiyong，et al）. Petri 网 在 电 力 系 统 中 的 应 用（Applications of Petri nets in power systems）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（5）：14-23.

[8]Binh P T T，Tuyen N D. Fault diagnosis of power system using neural Petri net and fuzzy neural Petri net[C]//IEEE Power India Conference.New Delhi，India，2006.

[9]文福拴，韩祯祥（Wen Fushuan，Han Zhenxiang）.基于遗传算法和模拟退火算法的电力系统的故障诊断（Fault section estimation in power systems using genetic algorithm and simulated annealing）[J].中国电机工程学报（Proceedings of the CSEE），1994，14（3）：29-35，6.

[10]文福拴，钱源平，韩祯祥，等（Wen Fushuan，Qian Yuanping，Han Zhenxiang，et al）.利用保护和断路器信息的电力系统故障诊断与不可观测的保护的状态识别的模型与Tabu 搜索方法（A Tabu search based approach to fault section estimation and state identification of unobserved protective relays in power systems using information from protective relays and circuit breakers）[J]. 电 工技术学报（Transactions of China Electrotechnical Society），1998，13（5）：1-8，51.

[11]刘道兵，顾雪平，李海鹏（Liu Daobing，Gu Xueping，Li Haipeng）.电网故障诊断的一种完全解析模型（A complete analytic model for fault diagnosis of power systems）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（34）：85-92.

[12]边莉（Bian Li）.基于交叉熵算法的唯相位控制方向图零点生成（Pattern null steering using the cross entropy method by controlling only the current phases）[J].信号处理（Signal Processing），2011，27（5）：791-794.

[13]Rubinstein Reuven Y. The Cross-Entropy Method：a Unified Approach to Combinatorial Optimization[M].Australia：Springer-Verlag New York Inc，2004.

[14]De Boer P-T，Kroese D P，Mannor S，et al.A tutorial on the cross-entropy method [J].Annals of Operations Research，2005，134（2）：19-67.

[15]文福拴，邱家驹，韩祯祥（Wen Fushuau，Qiu Jiaju，Han Zhenxiang）. 只利用断路器信息诊断电力系统故障的高级遗传算法（A refined genetic algorithm for fault section estimation using information from circuit breakers）[J].电工技术学报（Transactions of China Electrotechnical Society），1996，11（2）：58-64.

[16]刘道兵（Liu Daobing）.电网故障诊断的解析化建模与求解（Modeling and Solving of a Complete Analytic Model for Fault Diagnosis of Power Systems）[D].北京：华北电力大学电气与电子工程学院（Beijing：School of Electrical and Electronic Engineering，North China Electric Power University），2012.

[17]文福拴，韩祯祥，田磊，等（Wen Fushuan，Han Zhenxiang，Tian Lei，et al）.基于遗传算法的电力系统故障诊断的解析模型与方法——第一部分：模型与方法（An analytic model and genetic algorithm based methods for fault diagnosis in power systems Part 1：The model and method）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），1998，10（3）：1-7.

[18]Deng Libao，Qiao Liyan，Peng Xiyuan.A directed quantile cross-entropy method for 0/1 knapsack problems[C]//9th International Conference on Electronic Measurement and Instruments.Beijing，China，2009：319-322.

[19]文福拴，张勇，张岩，等（Wen Fushuan，Zhang Yong，Zhang Yan，et al）. 电力系统故障诊断与不可观测保护状态识别的解析模型（Analytical model for fault section estimation and state identification of unobserved protective relays in power systems）[J].华南理工大学学报：自然科学版（Journal of South China University of Technology：Natural Science Edition），2012，40（11）：19-28.