配电网中分布式电源最大准入容量优化配置

阎 鼎，包海龙，程浩忠，方 陈

（1.上海交通大学电力传输与功率变换控制教育部重点实验室，上海200240；2.上海市电力公司，上海200122）

目前，世界各国的电力专家公认大电网互联与分布式电源并网相结合的电力系统能够有效解决资源、负荷区位不一致的问题，增加电网稳定性，提高供电可靠性，优化发输配电经济性，改善电力系统灵活性等问题。分布式电源DG（distributed generation）是指直接布置在配电网或分布在负荷附近的发电设施[1]，一般容量在数千瓦至50 MW之间。分布式发电装置根据使用技术的不同，可分为热电冷联产发电、微型燃气轮机发电、小型水力发电、风力发电、太阳能光伏发电、燃料电池、储能设备等。

由于DG 接入配电网的容量与位置会对网络电压、潮流、网损等造成重大影响[2-4]，所以国内外学者对该领域做了大量研究。文献[5]讨论了DG 的经济与环境效益，分析了DG 并网及对常规电力系统规划、电能质量以及保护、可靠性等多方面的影响。文献[6]分别讨论了含DG 配电网的DG 选址定容与网络扩展规划问题。文献[7]以有功网损为优化目标，研究了DG 的规划方案。文献[8]研究了配电网电压分布特性，对分布式发电的可行接入位置以及注入容量限制进行了理论探讨。文献[9]以DG 并网容量最大为目标，采用智能算法对中压配电网DG 最大准入容量进行了研究。文献[10]建立了一种考虑DG 和地理信息因素影响的变电站综合优化规划模型。

因为配电网中DG 供电比例增大可减小传统机组的污染物排放量，所以DG 并网容量最大化也等价于环保效益的最优化。当前社会对环保越来越重视，故极有必要研究DG 的最大准入容量。但是网络中DG 渗透率较高时，若DG 的接入位置、数量与容量不合理，则会严重威胁系统的安全稳定运行。根据DG 安装容量大小以及DG 与负荷的位置关系，线路上的潮流既有可能增加也有可能减少。如果DG 出力大于该点负荷，则在该部分线路上就有可能出现反向潮流的状况。而由此可能会进一步引起诸如配电网保护控制问题，供电可靠性问题等。同时，DG 接入后，由于DG 输出无功以及线路传输功率的降低，线路各处电压会抬高。DG 接入位置越接近电源点，则线路电压分布受其影响越小；并网容量相同的DG 集中接入某一节点，其对电压的支撑效果不如DG 分散接入多个节点时的效果。因此，若配电系统中各节点电压普遍偏低，则DG 的接入对改善这一现象是有积极效果的，但也需要防止节点电压被抬高而越限。因此，在研究DG 最大准入容量时，需要通过合理配置DG 的接入位置、数量与容量，在确保网络安全稳定运行的前提下，实现DG 准入容量最大化。

基于某地区“生态岛”的定位与电网“低碳运行”的目标，本文重点研究以DG 最大准入容量为目标的配电网DG 优化配置问题，以期为DG 高比例、大容量接入配电网提供参考。

1 DG 优化配置模型的建立

本文建立了以所涉地块DG 并网容量最大为目标函数，引入多组涉及配电网投资经济性、运行稳定性、安全性、灵活性等多类型约束的规划模型。

为了量化DG 接入前后配电网各节点电压水平的变化，本文引入由支路电流法计算潮流方程时推导出的电压水平指标来表征各支路的电压水平[11-12]。在配电网潮流合理分布时，必然大于0，而配电网电压合理分布时，应当小于等于1，且越接近0，电压分布越优化。

1.1 目标函数

本文用于描述待规划地块并网DG 容量最大的目标函数为

式中：nDG为待选DG 接入节点；PDGi为第i 个接入点的DG 接入有功功率。该目标函数用于寻找配电网中DG 总有功接入最大的配置方案。

1.2 约束条件

1.2.1 潮流方程约束

在电网安全稳定运行的情况下，含DG 配电网的有功功率方程、无功功率方程以及节点电压方程如式（2）～（4）所示，将该3 个潮流方程作为式（1）目标函数的等式约束。即

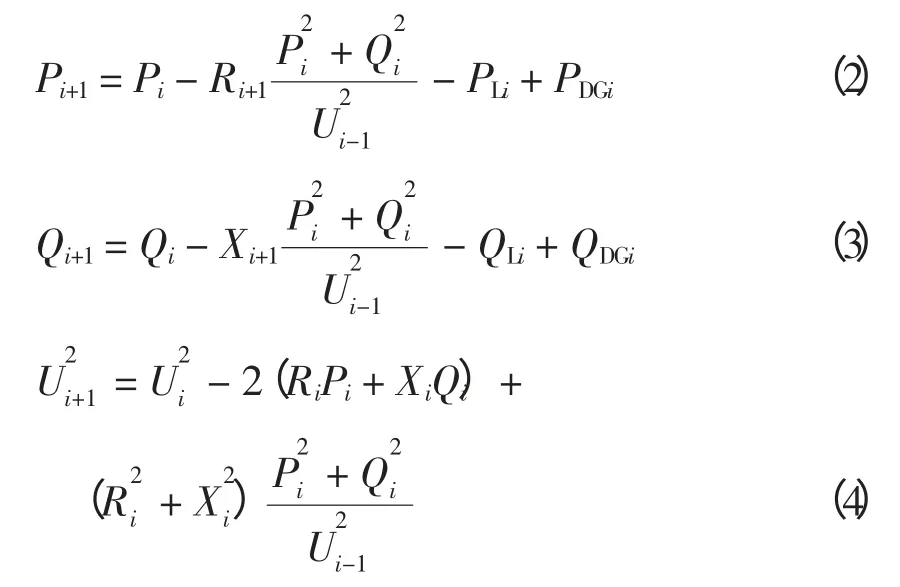
式中：Pi、Qi分别为第i 条支路上的有功、无功功率；Ri、Xi为第i 条支路上的电阻与电抗；Ui为第i个节点的节点电压；PLi、QLi为第i 个节点的负荷有功、无功功率；PDGi、QDGi为第i 个节点的DG 有功、无功功率。

1.2.2 节点电压约束

DG 的并网改变了配电网潮流的原有运行状态，对各节点的电压有抬升作用。根据我国国家标准GB/T 12325—2008《电能质量–供电电压偏差》的规定，20 kV 及以下三相供电电压偏差为标称电压的7%。由于本文的研究对象为10 kV 中压配电网，所以取7%为节点电压偏差的限定值。本文的节点电压约束方程为

式中，UN为节点额定电压。

1.2.3 电压水平与网损约束

改善配电网电压水平与降低网损是DG 投资的重要经济、社会、环保效益之一。所以本文要求DG 的投资目标是使配电系统电压水平改善，网损降低。

本文的网络电压水平与有功网损约束方程为

式中：LDG、Ldis为配电网加入与不加入DG 时的电压水平指标；Ploss.DG、Ploss.dis为配电网加入与不加入DG时的有功网损；ε1、ε2介于0～1 之间，根据具体规划方案对DG 并网后系统电压水平与网损的要求进行取值。

虽然近年来随着DG 的使用范围越来越大，安装成本也逐年降低，但是相对于传统大电网互联的电力系统运行方式，其投资运行费用依然偏高。所以需要对其投资运行总费用做出一定的限制。本文参照国内DG 的工程实际状况，取DG 单位容量设备综合成本和安装成本分别为430 万元/MW和120 万元/MW，DG 的维护运行费用为15 万/（a·MW）。对一定的规划周期，可根据上述经济性数据设定DG 投资运行总费用的上限CDGmax为

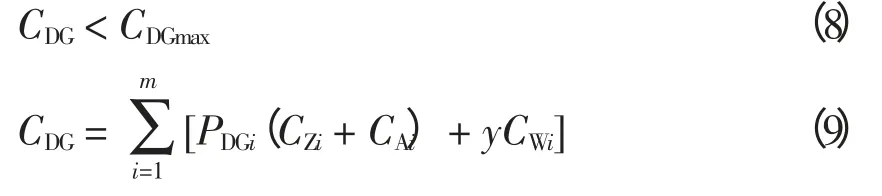
式中：CDG为一定规划周期内DG 的实际投资运行总费用；y 为DG 规划投资年限；CZi为第i 个DG 的单位容量设备综合成本，包括原动机成本、发电机成本与其他辅助设备成本等；CAi为第i 个DG 的单位容量安装成本；CWi为DG 的固定年维护成本。

1.2.5 约束条件汇总

除上述式（2）～式（8）的约束条件以外，本文还将考虑支路功率约束、系统旋转备用约束。除潮流方程以外，各约束条件汇总为

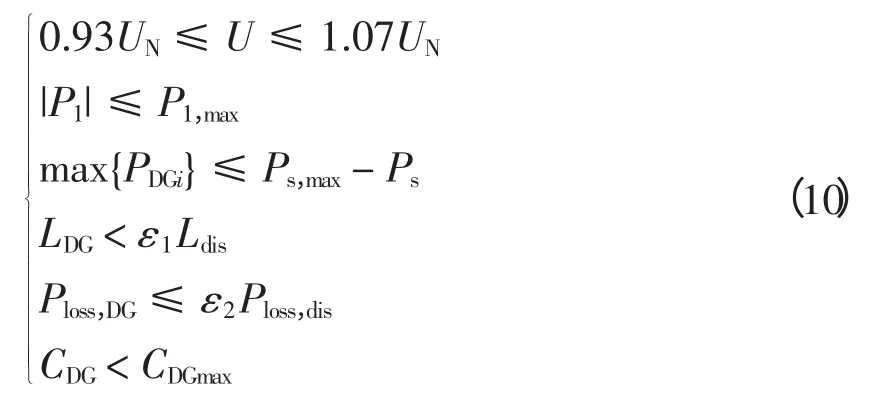
式中：P1、P1，max为配电网各支路的实际有功功率与最大有功功率限制；Ps为配电系统向输电系统购买的实际功率；Ps，max为配电系统向输电系统购买的最大功率。

2 求解方法

2.1 随机权重的粒子群算法

粒子群算法是一种群体智能算法，它是一种基于群体智能方法的演化计算，它的优势在于计算效果好、精度高、简单直观、容易实现、通用性强，既适用于科学研究又特别适用于工程优化问题[13]。

各类粒子群算法的优劣取决于其全局搜索能力与局部搜索能力。随机权重粒子群算法因其权重ω 在每次迭代中均随机生成，故其能较好地兼顾算法的全局与局部搜索能力。与线性权重粒子群算法相比较，它能克服两点不足：①如果粒子的初始位置与最优位置接近，则算法可能产生较小的权重ω，使粒子快速找到最优位置；②如果在初始阶段无法快速找到最优位置，那么线性递减的权重ω 会导致算法不能找到最优点，而ω 的随机生成则可以克服该局限[14]。随机生成的ω 计算公式为

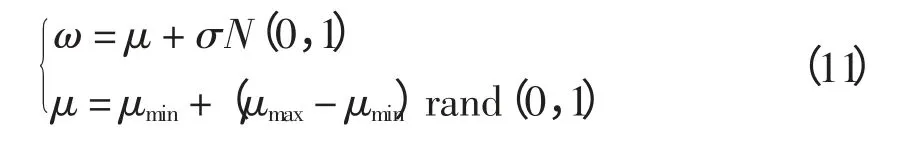
式中：rand（0，1）表示0～1 之间的随机数；N（0，1）表示标准正态分布随机数；μ 为平均随机权重；μmin为最小随机权重平均值；μmax为最大随机权重平均值；σ 为随机权重的方差。

由表1和表2可知，2013—2017年冬季细颗粒物污染主要出现在中度和重度 PM2.5等级，这两者的占比约为76%。而夏季却有近84%的污染是在轻度等级，且没有出现过重度污染情况（见表1）。夏季大气O3浓度达中度及以上，>160 µg·m-3的占比高达72.6%（见表2）。由此可知，贵阳市空气质量的变化与细颗粒物和光化学污染的季节性有关（王宏等，2011；王闯等，2015；严茹莎等，2013），即夏季细粒子减少和辐射增加使 O3浓度升高，冬季细颗粒物高排放和稳定边界层对大气扩散的不利影响是形成PM2.5重污染的主要原因。

2.2 基于随机权重粒子群算法的DG 优化配置步骤

本文基于随机权重粒子群算法的DG 优化配置步骤如下：

（1）输入网络原始参数与算法参数。本文取种群规模为80，μmin=0.5，μmax=0.8，σ=0.2；

（2）随机生成各个粒子的值和初始速度，计算网络潮流，求解目标函数，记录各粒子中的最大目标函数值Pbest（即DG 最大并网容量），各粒子的目标函数值FPbest以及最优粒子的位置Pos（即各待选DG 接入点）；

（3）更新迭代次数，由式（11）计算ω，然后更新各粒子的速度与位置信息；

（4）计算新的潮流与各粒子目标函数值，并与前次迭代结果比较，更新并记录各粒子中的最大目标函数值与粒子位置；

（5）判断是否达到最大迭代次数kmax，若达到，则终止程序，反之则重复步骤（3）和（4）；

（6）输出DG 最大并网容量与最优接入位置。优化配置流程如图1 所示。

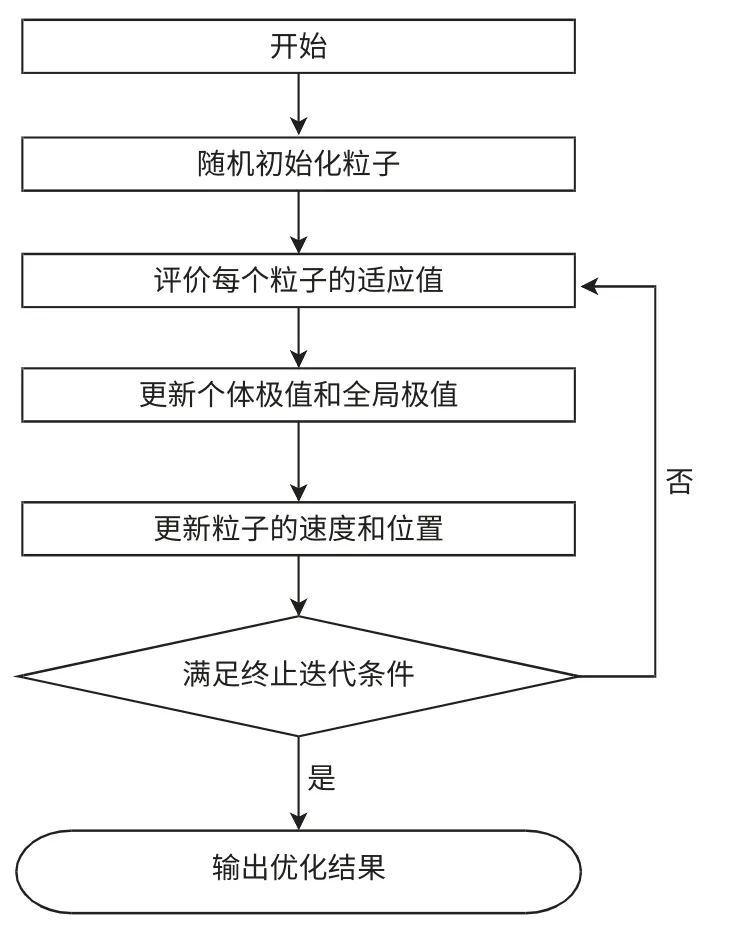
图1 DG 优化配置流程Fig.1 Flow chart of DG optimal allocation

3 算例分析

本文采用文献[15]的IEEE 33 节点标准配电网络作为测试系统，结构如图2 所示，其基准电压为12.66 kV，基准视在功率为10 MVA。本算例不规定DG 具体接入位置，而是给出待选位置集合，应用随机权重粒子群算法在满足模型各项约束的条件下，确定DG 的最优接入位置、数量与容量，求得DG 最大准入容量。待选节点集合为图2 中白色圆点所示。各待选节点若接入DG，则接入容量至少0.1 MW，并且低于该节点负荷需求，以防止反向潮流。否则不选择接入DG。本文将DG 作为PQ 节点处理，功率因数为0.9。该规划方案规定为70%。所研究地块的规划周期为5 a，5 a 的DG 投资预算为800 万元。

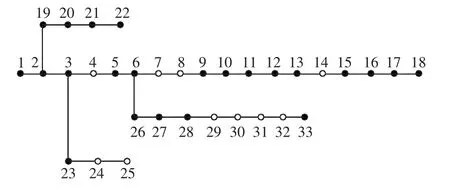
图2 IEEE33 节点配电系统Fig.2 IEEE 33-bus distribution system

表1 是不含DG 时的配电系统平均节点电压幅值Uave、最低节点电压幅值Umin、最高节点电压幅值Umax、有功网损Ploss，dis与DG 并网前的电压水平指标Ldis的计算结果。其中Umin、Umax分别出现在节点18 和1。

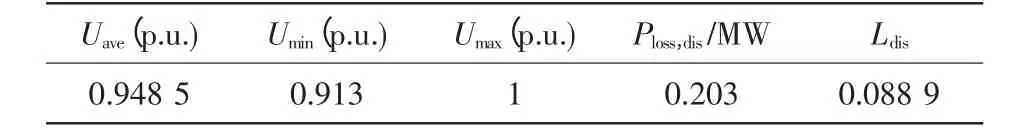
表1 不含DG 的配电系统计算结果Tab.1 Result of distribution network without DG

在DG 接入位置、数量与容量未知的情况下，本文采用随机权重粒子群算法求解第2 节所述模型。所得规划方案总共选取7 个节点接入1.24 MW的DG。具体优化配置结果如表2 所示。基于表2的DG 配置结果，对DG 并网后的网络平均节点电压幅值Uave、最低节点电压幅值Umin、最高节点电压幅值Umax、有功网损Ploss，dis与DG 并网后电压水平指标Ldg进行计算，结果如表3 所示。其中Umin、Umax分别出现在节点18 和1。

表2 DG 优化配置结果Tab.2 Results of DG optimal allocation

按表2 所示方案接入DG 后，配电系统的有功网损从0.203 MW 降低为0.105 MW，降低48.28%；电压水平指标从0.088 9 改善为0.061 4，节点电压优化；节点电压平均值从0.948 5（p.u.）提高至0.962 2（p.u.），节点电压最低值从0.913（p.u.）提高至0.930（p.u.），达到标准要求。该方案5 年实际投资额为775 万元，对预算资金的利用率较高，达到96.9%。此时该33 节点配电系统DG 接入总容量占该配电系统负荷总量的31.5%。

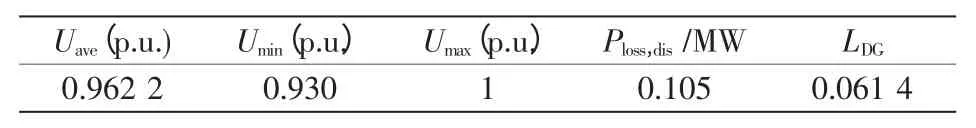
表3 DG 并网后的配电系统计算结果Tab.3 Result of distribution network with DG

由此可见，该DG 优化配置方案不仅保证了该方案下DG 高比例接入时的配电网安全可靠运行，而且降低了配电系统网损，改善了节点电压水平与网络电压分布。

4 结论

分布式发电作为一种有潜力的发电技术，是对传统大电网互联、集中式发电的有益补充。本文研究了配电网中DG 的优化配置问题，建立了以DG 接入容量最大为目标，充分考虑配电网安全、可靠、稳定运行的DG 优化配置模型，并应用随机权重粒子群算法求解。通过IEEE 33 节点标准算例测试，得到如下结论：

（1）本文所建立的DG 优化配置模型不仅使配电网DG 并网容量较高，且保证了配电网安全稳定运行，优化了网络电压分布，改善了节点电压水平，降低了配电系统运行时的有功网损；

（2）在本文所建立的DG 优化配置模型下，DG并网容量达到了负荷总量的31.5%，超过了一般的DG 规划并网容量，对配电网中大容量、高比例DG并网做了有益探索；

（3）在10 个DG 待选节点中，本文方案利用了7 个节点接入DG，DG 待选节点利用率较高。说明DG 分散接入能较好地改善节点电压水平。

作为DG 准入容量最大的优化配置问题，本文基于随机权重粒子群算法做了一定的探索。在日后的研究中，可以考虑引入其他智能算法做一对比研究，比较不同算法的优劣，得出最适应于寻求DG 最大准入容量的智能算法。

[1]Dugan R C，McDermott T E. Distributed generation[J].IEEE Industry Application Magazine，2002，8（2）：19-25.

[2]于建成，迟福建，徐科，等（Yu Jiancheng，Chi Fujian，Xu Ke，et al）.分布式电源接入对电网的影响分析（Analysis of the impact of distributed generation on power grid）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2012，24（1）：138-141.

[3]Kashem M A，Le An D T，Negnevitsky M，et al.Distributed generation for minimization of power losses in distribution systems[C]//IEEE Power Engineering Society General Meeting.Montreal，Canada，2006.

[4]Iyer H，Ray S，Ramakumar R.Voltage profile improvement with distributed generation[C]//IEEE Power Engineering Society General Meeting.San Francisco，USA，2005：2977-2984.

[5]丁明，王敏（Ding Ming，Wang Min）. 分布式发电技术（Distributed generation technology）[J].电力自动化设备（Electric Power Automation Equipment），2004，24（7）：31-36.

[6]王敏，丁明（Wang Min，Ding Ming）.含分布式电源的配电系统规划（Distribution network planning including distributed generation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2004，16（6）：5-8，23.

[7]朱勇，杨京燕，张冬清（Zhu Yong，Yang Jingyan，Zhang Dongqing）. 基于有功网损最优的分布式电源规划（Planning of distributed generation based on optimal real power losses）[J]. 电力系统保护与控制（Power System Protection and Control），2011，39（21）：12-16.

[8]王志群，朱守真，周双喜，等（Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi，et al）. 分布式发电接入位置和注入容量限制的研究（Study on location and penetration of distributed generations）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（1）：53-58.

[9]苏小玲，韩民晓，赵正奎，等（Su Xiaoling，Han Minxiao，Zhao Zhengkui，et al）.配电网中分布式电源最大准入容量分析（Research on maximum capacity of grid-connected distributed generation in distribution network）[J]. 电网技术（Power System Technology），2012，36（10）：87-92.

[10]刘自发，张伟，李可，等（Liu Zifa，Zhang Wei，Li Ke，et al）.考虑分布式电源的变电站优化规划（Substation optimization planning based on distributed generation）[J].电力建设（Electric Power Construction），2013，34（7）：37-42.

[11]陈海焱，陈金富，杨雄平，等（Chen Haiyan，Chen Jinfu，Yang Xiongping，et al）.配电网中计及短路电流约束的分布式发电规划（Planning for distributed generation in distribution network with short-circuit current constraints）[J]. 电力系统自动化（Automation of Electric Power Systems），2006，30（21）：16-21.

[12]刘健，毕鹏翔，董海鹏，等.复杂配电网简化分析与优化[M].北京：中国电力出版社，2002.

[13]李炳宇，萧蕴诗，汪镭（Li Bingyu，Xiao Yunshi，Wang Lei）.PSO 算法在工程优化问题中的应用（Application of particle swarm optimization in engineering optimization problem）[J].计算机工程与应用（Computer Science and Application），2004（18）：74-76.

[14]龚纯，王正林.精通Matlab 最优化计算[M].北京：电子工业出版社，2009.

[15]Baran Mesut E，Wu Felix F. Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Trans on Power Delivery，1992，4（2）：1401-1407.