空间溢出与我国经济增长：基于动态空间面板的方法

吉丹俊

(1.江苏联合职业技术学院 扬州分院， 江苏 扬州 225003；2.南京航空航天大学 经济与管理学院， 江苏 南京 210016)



空间溢出与我国经济增长：基于动态空间面板的方法

吉丹俊1,2

(1.江苏联合职业技术学院 扬州分院， 江苏 扬州 225003；2.南京航空航天大学 经济与管理学院， 江苏 南京 210016)

20世纪90年代以来，区域经济增长的空间溢出效应成为经济增长领域研究的热点问题，而随着空间计量技术的发展，对经济增长空间溢出效应的研究更加有效和准确。本文以柯布道格拉斯形式函数为基础同时考虑影响经济增长的相关因素，建立了区域经济增长的空间溢出效应理论模型，据此提出计量检验模型，并运用1997-2012年期间中国31个省份数据进行动态空间面板回归。首先进行模型选择和权重矩阵估计效率比较，最终确定两种权重矩阵使用包含时间固定效应的模型进行估计，估计结果显示当前经济增长具有正溢出效应，而这种溢出效应主要通过固定资产投资产生的。

经济增长； 空间溢出； 动态空间面板

一、引言

20世纪90年代以来，经济增长、经济地理及区域经济领域的研究者开始重点关注空间溢出在区域经济增长中的作用，也就是关注如何用区域间经济活动的交互性(不管是自发的还是非自发的)解释区域经济增长的动态性，从经济学角度来看，空间溢出效应主要是指地区经济活动产生的正外部效应，使得邻近地区获得无须补偿的发展优势[1]。

中国自1978年改革开放后实施市场经济，经济增长取得了令世界瞩目的成绩，在1978—2003年间实际GDP的年平均增长率达到9.5%左右[2]。虽然处在经济转型期的中国经济已完成大部分改革任务，但仍然具有一定程度的计划经济特征，比较明显的特征有：经济增长过度依赖投资，经济结构中制造业占比过高，国营企业规模较大以及政府干预经济发展的程度较高等[3]。此外，虽然发展市场经济后国内市场的统一可以促进地区间要素的流动进而产生非自发性溢出效应，然而各地政府为了保证达到GDP考核目标， 忽视区域协调发展，可能会产生负的空间效应。我国改革开放总设计师邓小平同志曾指出：“让沿海地区先发展，再带动内地发展”，这体现了利用空间溢出效应促进经济整体均衡发展的目的，因此，有必要借助计量模型检验地区间经济发展的空间溢出效应及其影响渠道，为政府制定整体的经济发展政策提供指导。

空间计量经济学是20世纪80年代以来计量经济学领域最伟大的发现之一。区域经济领域的实证分析使用的样本大多具有空间性质，而传统的计量方法大多基于高斯马尔科夫假设，无法解决具有空间性质样本面临的两个问题：(1)观察值之间的空间相关性(spatial dependence)；(2)空间异方差(spatial heterogeneity)性[4]。而空间计量经济学可以解决上述两个问题，经过该领域学者的努力，当前空间计量经济学已发展成为一门技术成熟的学科，逐渐成为区域经济领域实证研究主流计量方法，当前，空间计量模型既可以处理横截面数据也可以处理面板数据，并且自2000年以后，该领域的文献大量关注动态空间面板模型(dynamic spatial panels)，围绕模型的设定和估计方法展开了大量探索，依据Elhorst(2012)，和传统的计量模型相比，动态空间面板模型具有四大优势：(1)可以解决观察值在时间和空间上的序列相关性(serial dependence)；(2)可以解决观察值在每个时点上的空间相关性(spatial dependence)；(3)可以探索无法观测到的空间和时间效应；(4)可以解决由空间滞后或时间滞后因变量及自变量所引起的内生性问题[5]。该模型还可以估计自变量变化对本地区因变量的影响(即直接效应)及对邻近地区因变量(即间接效应或溢出效应)，因此，使用动态空间面板估计地区间经济发展的空间溢出效应将更有效、更准确。

二、文献述评

区域经济学大师Roberta Capello(2009)在一篇关于经济增长空间溢出效应的综述性文章中指出：当前研究空间溢出效应的文献主要关注三个领域，即知识溢出效应(knowledge spillovers)、产业联系溢出效应(industry spillovers)及经济增长溢出效应(growth spillovers)，具体解释见表1。其认为解释空间溢出效应产生的原因主要基于三个视角：空间地理视角(spatial-geographical approach)、区域功能视角(territorial-functional approach)和认知视角(cognitive approach)。空间地理视角认为空间只具有地理属性，空间溢出效应产生的原因是由于地理上的接近使得信息的交换、交易及市场关系更容易形成；然而学术界逐渐认识到空间地理视角的解释过于简单，20世纪90年代后期开始使用区域功能视角来解释，区域功能视角认为空间是区域功能的物理容器，而这些区域功能正是空间溢出效应形成的原因所在；在对上述两个视角进行批判的基础上Roberta Capello提出了认知视角，认为空间事实上是一系列附加值创造功能或活动的物理容器，而这些功能或活动主要存在于产业聚集地或城市区域，认知视角主要关注通过合作学习所产生的知识创造过程，而地理位置的邻近、网络关系、互动、创造力和重组能力会促进这种知识创造过程[1]。

表1 空间溢出效应：特征和性质

资料来源：参考文献[1] 。

当前，已有大量国际研究开始关注中国的区域经济空间溢出问题，使用的经验研究方法有VAR (vector-autoregressive，向量自回归)模型、传统计量模型和空间计量模型等。Brun,Combes & Renard[6](2002)使用1981-1998年间中国省域面板数据研究了东部沿海地区对中西部地区的经济发展溢出效应，结果显示中部地区比西部地区获得更多的溢出效应。Groenewold,Lee & Chen[2](2008)使用VAR模型研究了中国六个区域的经济溢出效应。Tian,Wang & Chen[7](2010)则借助于空间杜宾模型(Spatial Durbin Model)使用中国市域面板数据研究了城市间的空间溢出效应，结果发现城市间存在明显的正溢出效应，同时借助空间杜宾模型计算出的直接效应和间接效应可以更加细致地分析溢出效应的影响渠道。Bai,Ma & Pan[8](2012)则从市场潜力(market potential)的视角研究了区域间的经济溢出效应，基于中国省域面板数据利用固定效应模型在控制了其他影响区域经济增长的变量之后，发现市场潜力变量和地区经济增长水平正相关，而使用空间误差面板模型估计得到了同样的结果。Peng & Hong[9](2013)则基于中国的分行业面板数据运用空间面板模型研究了产业联系溢出效应，发现了行业间产业联系溢出效应。Scherngell,Borowiecki & Hu[10](2014)同样使用空间杜宾模型研究了我国知识资本和全要素生产率的关系，发现知识资本不仅对区域内全要素生产率有正向促进作用，还对邻近区域有正效应。

国内学术界也有一些研究从不同视角研究经济增长的空间溢出效应，相关研究有徐盈之、朱依曦和孙剑[11](2010)，张学良[12](2012)及张光南、洪国志和陈广汉[13](2013)等，在此不再一一列举。通过对上述文献的仔细研读发现，2000年之后的文献使用的计量模型基本是空间计量模型并且以面板模型为主，但是几乎没有文献使用动态空间面板方法，并且在这些使用空间计量模型进行估计的经验文献中对于空间权重矩阵的选取过于武断，没有探讨不同空间权重矩阵的估计效率，因此，使用动态空间面板模型研究我国经济增长的空间溢出效应并探讨不同空间权重矩阵对估计结果的影响将使得估计结果更加稳健，并可以给政策制定者提供更加丰富的政策建议。

三、理论模型

在本节将建立一个具有空间溢出效应特征的区域经济增长模型。影响经济增长的因素不仅对本地区的经济增长起积极作用还会对其他区域的经济增长产生正的溢出作用或负的溢出作用，具体情况需要做进一步的分析。

研究区域经济增长的空间溢出模型一般以柯布道格拉斯函数为起点，因此，本文以柯布道格拉斯形式函数为基础同时考虑影响经济增长的相关因素，将各个省份分别视为独立的实体，借鉴Scherngell，Borowiecki & Hu(2014)，建立如下形式的区域间经济溢出增长模型：

Qit=Q(Xit)

(1)

在上式中，i=1,…,N，表示有N个区域，t=1,…,T表示时间，Xit为包含具有空间溢出效应并影响经济增长这些因素的函数。当前，经济增长理论认为影响经济增长的因素主要有劳动力、物质资本、人力资本、技术进步及企业家精神等，此外，在开放经济中，一个国家的对外开放程度也会影响经济增长。因此，假设Xit包含劳动力、物质资本存量、对外开放程度、人力资本、企业家精神和创新精神，其具体形式如下：

由于假定Qit为柯布道格拉斯形式，因此，其具体形式可以写成：

τt表示影响产出的时间趋势，εit为扰动项，α1,α2,…,α12为各因素的投入产出弹性。而对于外溢效应因素，如Kit*我们将其定义为：

(4)

wij表示空间折旧因子，代表区域i吸收其他区域外溢效应的能力。其他5个具有外溢效应因素的定义方法类似。

对式(3)两边取对数并进行一阶差分，得到如下表达式：

这样，我们就建立了一个区域经济增长的空间溢出模型，(5)式中的α1,α2,…,α12即为需要估计的参数。

四、计量方法与结果分析

(一)模型设定和估计方法

基于Elhorstetal.[14](2013)，建立一个动态空间面板模型(DynamicSpatialPanel)进行计量分析，其表达式为：

Yt=τYt-1+ρWYt+ηWYt-1+Xtβ+μ+αtlN+εt

(6)

Yt表示某一时间点(t=1,…,T)上N个地区的因变量观察值，为N×1向量；而Xt是一个N×K矩阵，表示K个外生解释变量；W表示空间权重矩阵，是一个N×N矩阵，矩阵中的每个元素表示各地区和其他地区的空间关系，对角线元素为0；WYt表示因变量具有同期的空间自相关性，WYt-1表示滞后一期的空间自相关性，ρ一般被称作空间自相关系数，η为滞后的空间自相关系数；εt=(ε1t,…,εNt)T为独立同分布、期望值同为0、方差同为σ2扰动项所组成的向量；μ=(μ1,…,μN)T表示地区固定效应向量，用来控制具有地区特征而不随时间变动的变量，αt表示时间固定效应系数，lN是一个组成元素全为1的N×1向量，同时考虑地区固定效应和时间固定效应可以减少面板模型的估计偏差。

对于动态空间面板模型，Yu等[15](2008) 在仅包含地区固定效应模型中使用准极大似然估计法(QuasiMaximumLikelihood)进行估计，这种方法在扰动项不服从正态分布的情况下而假定服从正态分布 ，而Lee等[16](2010)在既包含地区固定效应又包含时间固定效应的模型中使用同样的方法进行了估计，在这两篇文献中，作者均讨论了在n和T可以很大情况下估计结果的渐进性。此外， Lee等[17](2010)指出对于τ、ρ、η，还应满足τ+ρ+η<1，这样的模型才是稳定的，如τ+ρ+η>1，则该模型将出现类似于时间序列模型中的空间协整(spatialcointegration)问题，如τ+ρ+η>1，则出现爆炸根(explosiveroots)问题，对于空间协整问题和爆炸根问题可以通过空间一阶差分(spatialfirst-differences)解决，即对式(6)左右两边同乘以矩阵(I-W)，I为N阶单位矩阵。为了衡量该模型的空间溢出效应，基于Lesage等[18](2009)计算横截面数据模型直接效应(directeffect)和间接效应(indirecteffect)的方法，对式(6)做适当变形，可以给出动态空间面板模型各解释变量直接效应和间接效应的估计方法。

式(6)可以写成：

Yt=(I-ρW)-1(τI+ηW)Yt-1+(I-ρW)-1Xtβ+(I-ρW)-1(μ+αtlN+εt)

(7)

在上式中，固定时间t，对向量Yt针对第k个解释变量求偏导，则得到一个N×N矩阵：

该偏导矩阵对角线元素表示直接效应，非对角元素表示间接效应，同时可以看出式(8)等式右侧跟时间没有关系， Lesage等(2009)通过计算该偏导矩阵对角线元素平均值的方法来衡量直接效应，而通过计算所有非对角元素平均值的方法来衡量间接效应，间接效应和直接效应的加总为总效应。同样道理，在(7)式中，对向量Yt针对向量Yt-1求偏导可以得到：

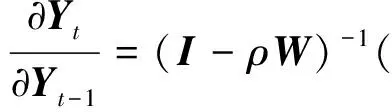
(9)

对于该偏导矩阵同样使用Lesage & Pace(2009)的方法可以计算出Yt-1对Yt的直接效应和间接效应。

因此，我们将基于Elhorst等(2013)，Lee等(2012)及Lesage等(2009)的估计方法对式(6)进行估计。

(二)数据与变量说明

研究所用原始数据均来自于历年《中国统计年鉴》《中国劳动统计年鉴》《新中国60年统计资料汇编》及国泰安数据库，由于部分地区和年份数据无法获得，剔除这些地区和年份，最后形成的数据集合包括从1997—2012年间31个中国省、直辖市及自治区的经济变量。各变量的统计特征见表2。

空间权重矩阵W：W=(wij:i,j=1,…,N)，权重矩阵反映不同地区的空间位置关系，我们的样本来自中国大陆31个省、市及自治区，因此W是一个31阶方阵，其空间权重元素wij表示地区i对于地区j的空间影响，对于空间自我影响，也就是wii的值我们遵循一般做法假定wii=0，wii为空间权重矩阵的对角线元素，对于该矩阵非对角线元素的构建方法一般有两大类：一种是基于边界的权重值选取，另一种是基于距离的权重值选取，我们对于非对角线元素的构建也将涵盖这两大类，主要包括以下三种：

表2 变量描述性统计表

(1)空间相邻权重(SpatialContiguityWeights)0-1型。我们通过区域是否相邻的方法来确定矩阵中每个元素的值，根据地图上所研究区域的相对位置，决定哪些区域是相邻的，并用“0-1”表示，即“1”表示空间单元相邻、“0”表示空间单元不相邻，该矩阵中对角线元素全部为“0”，因为自身不可能和自己相邻，并且该矩阵是一个对称矩阵。

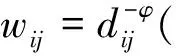
(3)距离指数权重(ExponentialDistanceWeights)。该方法同样假定空间权重随距离增加而递减但其衰减的方式为以e为底的指数函数形式：wij=exp(-θdij)，θ为任意大于0的常数，在这里我们选取θ=0.01、0.02和0.03。

这样，我们一共设定了7种空间权重矩阵，在模型估计时我们将对这些权重矩阵进行行标准化，也就是使得每行元素的和为1。

(三)计量结果

1.模型选择

运用MATLAB软件动态空间面板估计工具箱对本文选取的面板数据依次对7种空间权重矩阵进行模型选择的检验，首先通过F检验判别模型中是否应包含时间哑变量(timedummies)，也就是是否应包含时间固定效应；然后通过Wald检验判别是否有空间协整或爆炸根问题，如果有则应进行空间一阶差分，模型选择检验结果如表3所示：

表3 模型选择检验结果

对于空间相邻0-1型权重矩阵，时间固定效应F检验的P值小于0.01，所以应选择包含时间固定效应模型，然后在该模型下估计出τ+ρ+η的值为0.6591，Wald检验P值小于1%，模型是稳定的，不需要做空间一阶差分；对于距离幂权重，当φ=1，1.5，2时，时间固定效应F检验P值均大于5%，均应选择不包含时间固定效应模型，并且在该模型下τ+ρ+η的值均小于1并且Wald检验P值均小于1%，所以这三种权重矩阵均不需要做空间一阶差分；对于距离指数权重，当θ=0.01，0.02，0.03时，时间固定效应F检验P值均小于1%，均应选择包含时间固定效应模型，进一步计算出τ+ρ+η的值均小于1并且Wald检验P值均小于1%，因此均不需要做空间一阶差分。

表4 各空间权重矩阵估计效率比较

2.估计结果

选取0-1型权重和距离指数权重(θ=0.03)利用MATLAB动态空间面板工具箱对数据进行估计，估计出各自变量的回归系数、直接效应、间接效应和总效应结果如表5和表6所示：

在表4中，使用的权重矩阵为空间相邻0-1型权重，W*Yt的回归系数为0.240 0并且在1%水平显著；Yt-1的直接效应为-0.150 8并且在10%水平下显著，其间接效应为0.637 3并且在1%水平下显著；ΔlnKit的直接效应为8.923 8并且在1%水平显著，其间接效应为2.764 8并且在5%水平显著；其余自变量的直接效应及间接效应均不显著。在表5中，使用的权重矩阵为距离指数权重(θ=0.03时)，W*Yt的回归系数为0.106 4并且在5%水平显著；Yt-1直接效应不显著，间接效应为0.637 3并且在1%水平显著；ΔlnKit直接效应为8.789 2并且在1%水平显著，其间接效应为1.025 3并且在10%水平显著；其余自变量的直接效应及间接效应均不显著。比较表5和表6的估计结果可以发现：W*Yt回归系数均为正且显著，说明地区经济增长具有正的空间溢出效应，Yt-1的间接效应均为正且显著，说明滞后一期的经济增长对其他地区经济增长具有正向促进作用，ΔlnKit的直接效应均为正且显著，其间接效应也均为正且显著，说明资本存量的增加对于本地和其他地区的经济发展都有正向促进作用。表5和表6的结果基本一致，这也间接说明了我们的估计结果是稳健的。

表5 动态空间面板估计结果(空间相邻0-1型权重矩阵)

说明：括号内表示近似t值，显著度使用双侧Z检验，1)表示10%水平显著，2)表示5%水平显著，3)表示1%水平显著。

表6 动态空间面板估计结果(距离指数权重，θ=0.03)

注：括号内表示近似t值，显著度使用双侧Z检验，1)表示10%水平显著，2)表示5%水平显著，3)表示1%水平显著。

五、结论和政策含义

基于经济增长的空间溢出视角，本文认为区域经济增长会带动其他区域的增长潜力，在考虑相关影响经济增长因素之后，建立了一个影响区域经济增长的柯布—道格拉斯型的空间溢出理论模型，在此基础上建立我们的计量检验模型，使用中国大陆地区31个省级行政区域1997-2012年期间面板数据进行动态空间面板回归，在对各参数进行估计之前，首先讨论了各种权重矩阵的最佳估计模型进而检验了在最佳估计模型情况下何种权重矩阵估计效率最高，最终确定空间相邻0-1型权重矩阵和距离指数权重(θ=0.03)矩阵进行估计，两种权重的估计结果显示：地区经济增长具有正的空间溢出效应，资本存量的增加对于本地和其他地区的经济发展都有正向促进作用，而其他因素对经济增长效果不明显。资本存量的增加主要是由固定资产投资产生的，因此，当前我国经济增长的主要驱动力为固定资产投资。据此提出相应的政策建议：政府应转变经济增长方式，避免经济增长过度依赖固定资产投资，政府应鼓励创新和创业、促进人力资本积累，积极推进经济增长方式向“创新推动型”增长准备；此外，各地政府应加强区域间的经济合作，避免“诸侯经济”，促进要素、人才和知识的有效流动，为经济发展的空间溢出提供良好的土壤，最终实现经济同步增长、共同繁荣。

注释：

①平均受教育年限的计算公式：(接受小学教育人数×6+接受初中教育人数×9+接受高中或中专教育人数×12+接受大学教育人数×16)/地区总人数

[1]CapelloR.Spatialspilloversandregionalgrowth:acognitiveapproach[J].EuropeanPlanningStudies,2009,17(5):639-658.

[2]GroenewoldN,LeeG,ChenA.Inter-regionalspilloversinChina:theimportanceofcommonshocksandthedefinitionoftheregions[J].ChinaEconomicReview,2008,19(1):32-52.

[3]YaoY.TheChinesegrowthmiracle[J].HandbookEconomicGrowth,2014(2B):943-1031.

[4]LesageJP.Thetheoryandpracticeofspatialeconometrics[M].Toledo:TheTheoryandPracticeofSpatialE￣c￣o￣n￣o￣m￣e￣t￣r￣i￣c￣s,1999：122.

[5]ElhorstJP.Dynamicspatialpanels:models,methodsandinferences[J].JournalofGeographicalSystems,2012(14):5-28.

[6]BrunJF,CombesJL,RenardMF.AretherespillovereffectsbetweencoastalandnoncoastalregionsinChina?[J].ChinaEconomicReview,2002,13(2/3):161-169.

[7]TianL,WangHH,ChenY.SpatialexternalitiesinChinaregionaleconomicgrowth[J].ChinaEconomicReview,2010,21:20-31.

[8]BaiC,MaH,PanW.SpatialspilloverandregionaleconomicgrowthinChina[J].ChinaEconomicReview,2012,23(4):982-990.

[9]PengL,HongY.Productivityspilloversamonglinkedsectors[J].ChinaEconomicReview,2013,25:44-61.

[10]ScherngellT,BorowieckiM,HuY.EffectsofknowledgecapitalontotalfactorproductivityinChina:Aspatialeconometricperspective[J].ChinaEconomicReview,2014,29:82-94.

[11]徐盈之,朱依曦,孙剑.知识溢出与区域经济增长:基于空间计量模型的实证研究[J].科研管理,2010(6):105-112.

[12]张学良.中国交通基础设施促进了区域经济增长吗——兼论交通基础设施的空间溢出效应[J].中国社会科学,2012(3):60-77.

[13]张光南,洪国志,陈广汉.基础设施、空间溢出与制造业成本效应[J].经济学,2013,13(4):285-304.

[14]ElhorstP,ZandbergE,DeHaanJ.Theimpactofinteractioneffectsamongneighbouringcountriesonfinancialliberalizationandreform:adynamicspatialpaneldataapproach[J].SpatialEconomicAnalysis,2013,8(3):293-313.

[15]YuJ,deJongR,LeeL.Quasi-maximumlikelihoodestimatorsforspatialdynamicpaneldatawithfixedeffectswhenbothnandTarelarge[J].JournalofEconometrics,2008,146(1):118-134.

[16]LeeL,YuJ.Aspatialdynamicpaneldatamodelwithbothtimeandindividualfixedeffects[J].EconometricTheory,2010,26(2):564-597.

[17]LeeL,YuJ.Somerecentdevelopmentsinspatialpaneldatamodels[J].RegionalScienceandUrbanEconomics,2010,40(5):255-271.

[18]LesageJ,PaceRK.Introductiontospatialeconometrics[M].BocaRaton:CRCPress/Taylor&FrancisGroup,2009：121.

[19]单豪杰.中国资本存量K的再估算:1952～2006年[J].数量经济技术经济研究,2008(10):17-31.

[20]YuY.CHINA_SPATDWM:StatamoduletoprovidespatialdistancematricesforChineseprovincesandcities[EB/OL].(2009-12-22)[2015-09-20].https://ideas.repec.org/c/boc/bocode/st57059.html.

(责任编辑：沈秀)

Spatial Spillover and Economic Growth of China:a Spatial Dynamic Panel Data Approach

Ji Danjun1,2

(1.Yangzhou College, Jiangsu Union Technical Institute, Yangzhou 225003, China;2. College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Ever since the 1990s, there has been growing research interest in spatial spillovers of regional economic growth, and as the technique of spatial econometrics reaches its maturity, it enables more efficient and accurate empirical research on spatial spillover. In this paper, a Cobb-Douglas-Type theoretical model on spatial spillover of regional economic growth is built considering related factors for economic growth, based on which the econometric model is formulated. Using a panel data set from years of 1997 to 2012 of 31 Chinese provinces, a dynamic spatial panel model is estimated. First, the model is selected and weight matrix estimation efficiency is compared, and then two kinds of spatial weight matrices with time-period fixed effect that best describe the data are found out. The estimation results reflect positive spillover effects of the present economic growth, which is achieved mainly by fixed capital investment.

economic growth; spatial spillover; dynamic spatial panel model

2015-10-20

吉丹俊(1983—)，男，江苏扬州人，博士研究生，讲师，主要从事区域经济、空间计量研究。

F061.2

A

2095-042X(2015)06-0033-08

10.3969/j.issn.2095-042X.2015.06.006