集成立轴风机的高层建筑二维模型动态数值分析

彭 伟 张祖鹏 张 伟,2 陈国平

(1.西南科技大学土木工程与建筑学院 四川绵阳 621010；2.中国科学技术大学 安徽合肥 230027)



集成立轴风机的高层建筑二维模型动态数值分析

彭 伟1张祖鹏1张 伟1,2陈国平1

(1.西南科技大学土木工程与建筑学院 四川绵阳 621010；2.中国科学技术大学 安徽合肥 230027)

采用标准k-ε湍流模拟方法，在不考虑风力机与建筑连杆及风力机叶尖损失的影响下，采用滑移网格技术，对风力机与建筑一体化二维模型在不同风速下进行动态研究。结果表明：在不同风速下，建筑迎风面风力机的转矩系数最大值为0.41，最小值为0.10；背风面风力机的转矩系数最大值为0.27，最小值为0.17。

标准k-ε湍流模拟方法 立轴风力机 高层建筑 风荷载 转矩系数

随着全球经济活动的加剧，能源消费也在加速发展，甚至超过了能源储藏的潜在能力。风能是可再生能源体系的重要组成部分，具有资源分布广、开发潜力大、环境影响小、可永续利用以及易于转化等特点，所以日益引起人们的重视。目前，风能的主要利用形式是建立风力发电场，运用风力机将风能转化为电能。但风电场都远离城市，城市风能的利用非常少，将风力机应用于城市环境，与建筑有机结合，开发城市风能，在倡导发展绿色建筑和低碳经济的今天具有十分积极的意义。

风力机与建筑相结合，能有效利用城市风力资源，省去了传统大型风力机的远距离能源传输，使得输运过程中的能源消耗大大降低，有效提高风能利用率，而且省去了单纯大型风力机繁琐的支架。风力机与建筑一体化结构为节能减排的新型建筑形式，将绿色节能的环保概念与建筑结构结合起来，开创了建筑设计的新思路、新方法。

目前，部分学者对风力机建筑一体化系统进行了可行性研究。大多数学者认为，将风力机等风能设备与不同种类的建筑物结合起来，为建筑物提供电力等能源，满足日益增加的功能需求是可行的，但有一定的局限性，如Ziyad Salameh[1]，Zhu Zhenglin[2]。Islam Abohela[3]提出要建造环境友好型建筑，在屋顶上安放风力机是一种可行的办法，他采用CFD方法研究了屋顶形状、建筑高度、来流方向以及都市建筑布局对风力机安装位置的影响。

风力机与建筑结合，主要的问题是如何降低风力机产生的噪音问题，部分学者针对此问题，对应用到建筑上的风力机进行了设计，众多的学者认为，小型风力机运用到建筑物，能有效降低风力机产生的城市噪音，例如J.J.H.Paulides[4]提出了一种小型的水平轴文丘里管(直径2 m)风力机；Tim Sharpe[5]提出了一种交叉环状结构的新型小型垂直轴风力机。

此外，研究者们通过风洞实验、数值模拟等方法对各种形状的建筑上的风载荷、风压特性等进行了研究，如:Yong Chul Kim,Jun Kanda[6];L.Rosa,G.Tomasini等[7];Yi Yang,MingGu等[8];Shenghong Huang[9]等。

调研发现，对风力机与建筑一体化结构在风载荷作用下风力机的转矩系数以及整个流场的物理特性的研究较少，因此，本文以垂直轴风力机与高层建筑相结合的模型作为研究对象，采用k-ε标准湍流模拟方法，在不考虑风力机与建筑连杆及风力机叶尖损失的影响下，采用滑移网格技术，对风力机与建筑一体化二维模型在不同风速下进行动态数值分析。

1 控制方程和滑移网格模型

1.1 控制方程

湍流模式理论是以雷诺平均方程与脉动运动方程为基础，引入一系列的湍流模型假设，建立起一组描述平均量的封闭方程组。标准的k-ε模型是个半经验公式，是从实验现象中总结出来的，它有适用范围广、经济、精度合理的特点。标准的k-ε二方程模型假定湍动黏度μi是各向同性的，其基本输运方程为：

G+G-ρε-YM+Sk

(1)

(2)

式中：Gk是由于平均速度梯度引起的湍动能产生项；Gb是由于浮力引起的湍动能k的产生项；YM代表可压缩湍流中脉动扩张的贡献；C1ε，C2ε和C3ε为经验常数；αk和αε分别为与湍动能k和耗散率ε对应的普朗特数；Sk和Sε是用户定义的源项。

1.2 滑移网格原理

根据风力机的转动性质，本次研究中，采用Fluent中的动网格技术——滑移网格。

滑移网格(MovingMesh)的基本原理[10]是将几何模型网格划分成几个区域,交界面两侧的网格相互滑动,而不要求交界面两侧的网格结点相互重合,但要计算交界面两侧的通量,使其相等。为了计算交界面的通量,首先在每一个新的时间步确定出交界面两边交界区的重合面。基本上,通过网格重合面的通量由交界面两边交界区的重合面计算。交界面区域是由A-B，B-C和D-E，E-F所组成。这两个区域的相交产生d-b，b-e和e-c,两个网格单元区块在d-b，b-e和e-c上的重叠构成了内部区域。为计算通过单元 Ⅲ 的通量(D-E上),在计算过程中将不考虑D-E,而是由d-b和b-e来代替,通过d-b和b-e分别由单元I和单元Ⅱ把流场信息带入到单元Ⅲ中。

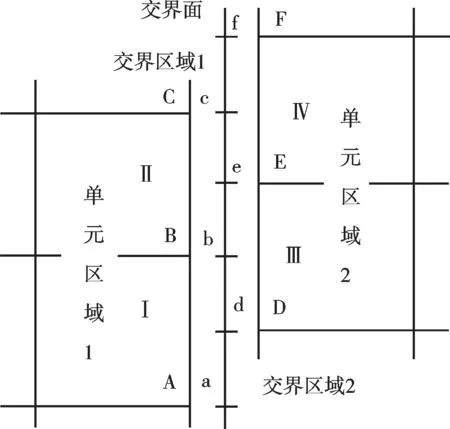
图1 静止网格与滑移网格数据传递原理图Fig. 1 Stationary grid and sliding mesh data transmission principle diagram

2 物理模型及计算区域

2.1 物理模型

该模型为风力机与凹角建筑相结合的二维模型，如图2所示。建筑物平面尺寸为：长×宽=34 m×34 m，表面平整，无任何附属物；风力机的平面尺寸为：长×宽=2 m×2 m, 4个叶片分别成90°夹角，4个风力机的编号分别用#1，#2，#3，#4表示，并假设风力机叶片为直叶片，安装在建筑的四个凹角上。

2.2 计算区域及网格划分

选择的实际计算流域为:入流边界到建筑模型取7D；出流边界到建筑模型取22D；建筑物侧面到流域两个侧面的距离均为5D；总流域为：长×宽=1 020 m×374 m。计算区域见图3所示。

划分网格时忽略风力机叶片的厚度，利用Gridgen软件建立整体结构网格，整体网格共分44个块。网格建立完成后进行雅克比的检验，以保证网格质量。网格总量为629 000。计算区域局部网格示意图如图4所示。

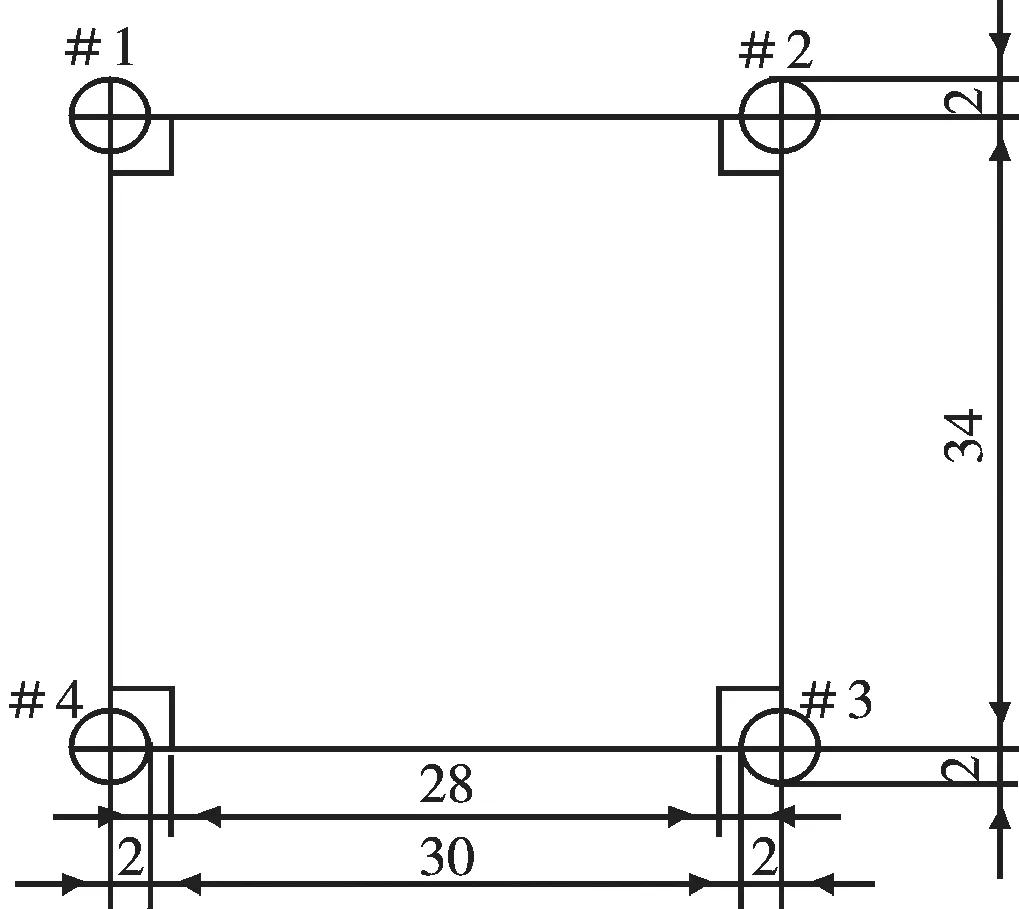
图2 二维模型示意图Fig. 2 Schematic diagram of two-dimensional model

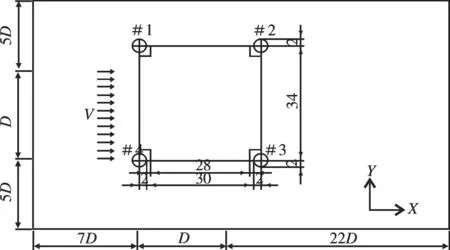
图3 计算区域示意图Fig.3 Sketch map of regional calculation model

图4 局部网格示意图Fig.4 Schematic diagram of local grid

3 边界条件及求解器设定

3.1 边界条件设定

进口边界条件采用速度入口(velocity-inlet)，出口边界条件采用压力出口(pressure-outlet)。在侧面边界条件设置时，考虑将建筑物置于无限大的空间下，因此侧面边界同样采用速度入口型边界。建筑壁面和风力机壁面：直接采用滑移壁面(wall)。

风力机旋转边界条件设置：因现已有的垂直轴风力机额定转速为12 rad/s，本次研究时，人为设定风力机的转速均为12 rad/s且沿着顺时针方向旋转。

3.2 求解器设定

采用基于压力的隐式算法，将离散的非线性控制方程线性化为在每一个计算单元中相关变量的方程组。流动为非定常流动，采用标准k-ε湍流模型计算，不考虑空气的自重与传热。采用压力速度耦合算法SIMPLE，压力采用标准压力(Standard)，动量、湍动能、湍流耗散率均采用二阶迎风格式。连续

性方程、各个速度方程、湍动能k以及湍流耗散率ε的收敛残差均设定为10-5，计算时间步长为0.01。

4 计算结果分析

4.1 转矩特性分析

风力机的转矩特性主要为风力机传动系统和发电机设计时提供转矩。风叶转矩的大小直接决定了风轮的整体转矩，是风能转化为机械能的一个重要特性，转矩系数定义如下：

式中：M-表示风叶转矩；ρ-来流密度；S-风轮迎风面积；R-风轮的半径；V∞-来流速度。

在本次研究中，取建筑高度H=80 m，100 m处的风速进行计算，根据《风工程与工业空气动力学》相关知识[11]：在C类地貌10 m参考高度不同风速下，在建筑物80 m，100 m高度处所对应的风速分别不同，如表1所示。

表1 不同高度处对应的风速Table 1 Wind speed at different heights

由于计算模型为对称模型，选取相对于来流风向的1/2界面进行转矩系数分析。即：分别分析#1，#2风力机在同一风速下的不同的转矩系数及在不同风速下的转矩系数。

4.1.1 不同风速下#1，#2风力机转矩系数对比分析

从图5可以看出，风力机每旋转90°，转矩系数就恢复到初始位置，出现周期性的变化，这与实际的情况相符，验证了本次研究的准确性以及可行性。

通过风力机的转矩系数变化曲线，可以看出：#1风力机，在不同来流风速时，叶片的转角θ为45°～75°，135°～165°，225°～255°及315°～345°之间时，其转矩系数最大，约为0.37～0.41；而当叶片旋转到90°～120°，180°～210°，270°～300°之间时，风力机的转矩系数则最小，其值约为0.10～0.15。分析其原因：主要是当来流风遇到钝体时要向钝体两侧分流，此时在建筑的拐角处产生较大的分离流动，叶片的转角转动到45°左右时，风力机迎风面靠近外侧处的风速较内侧的风速大得多，且来流的流动方向与风力机的转动方向相同，因此风力机的整体转动系数较大。

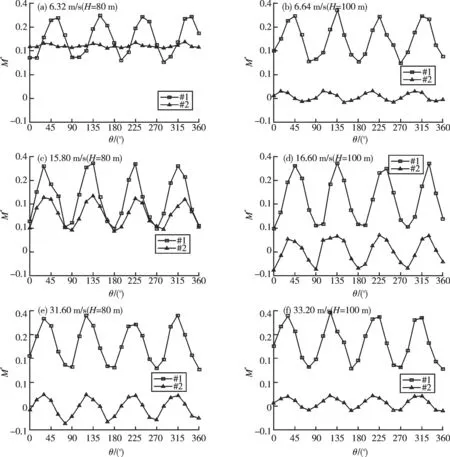
图5 不同风速下#1，#2风力机转矩系数值Fig. 5 Torque coefficient of #1,#2 Wind turbine with different wind speeds

#2风力机，当来流风速在6.32 m/s时，其转矩系数基本上维持在0.22左右。但是随着风速的增大，其转矩系数出现正负交替的变化趋势，当叶片的转角θ在0°～30°，90°～120°，190°～210°，285°～315°之间转动时，其值为正值；在45°～75°，135°～165°，225°～255°转动时为负值。其值的变化范围在 5%之间。分析其原因：对于#2风力机，处于建筑的背风面处，在来流风速较小时，建筑背风面的旋涡脱落及侧面的湍流较弱，对风力机的转矩系数影响不大，其值保持稳定，在风速增大后，由于受背风面旋涡脱落的影响增大，转矩系数波动较大。

4.1.2 同一风力机在不同风速时转矩系数对比分析

#1风力机在H=80 m，100 m处，不同风速时转矩系数对比如图6所示。

从图6可以看出：#1风力机在不同的高度、不同的来流风速时，所有转矩系数曲线均按周期性变化，最大值为0.41，最小值为0.10，转矩系数最大值均出现在来流风速最大时，最小值则出现在来流风速为15.80 m/s和16.60 m/s 时。

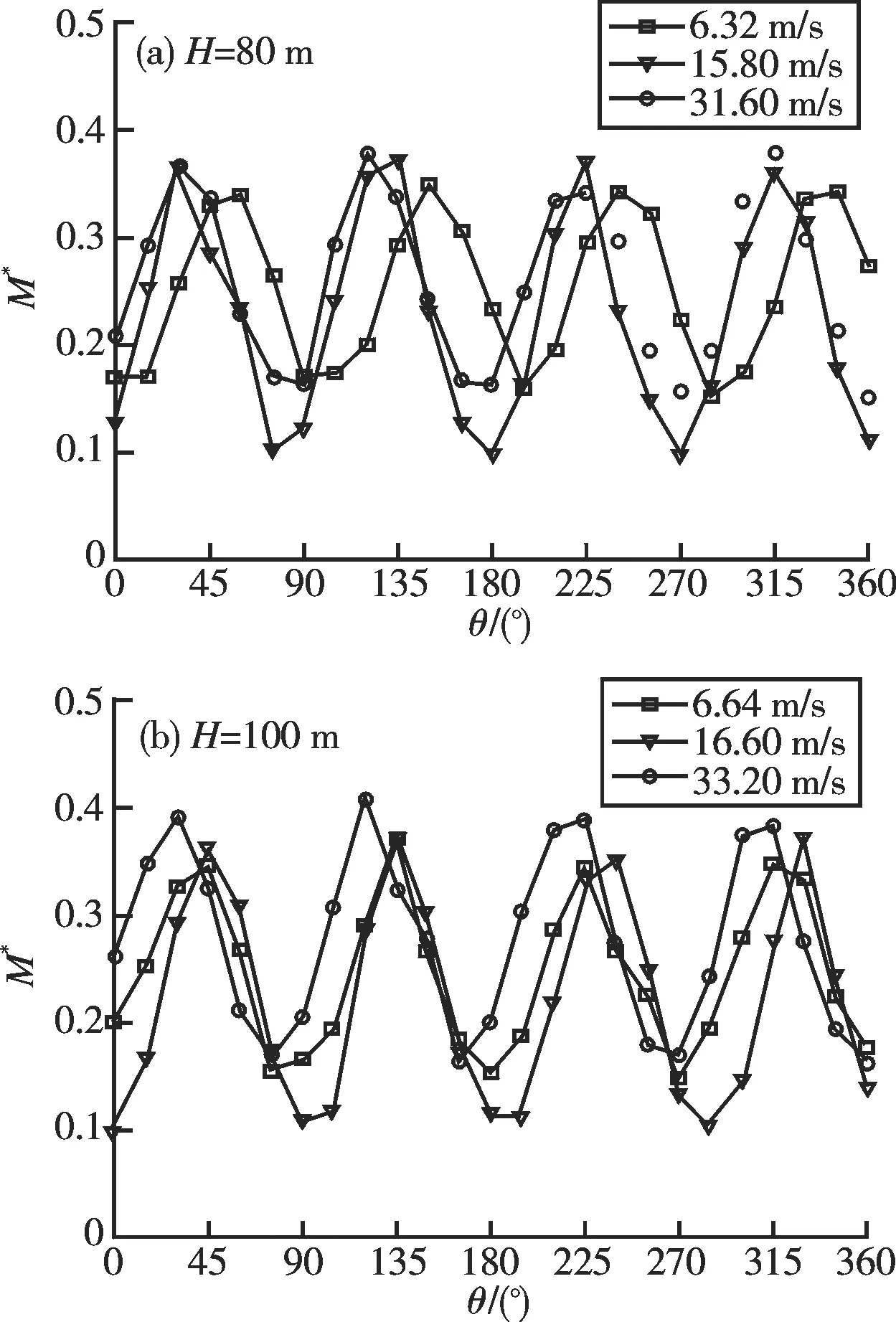
图6 #1风力机不同风速时的转矩系数Fig. 6 Torque coefficient of #1 wind turbine at different wind speed

#2风力机在H=80 m，100 m处，不同风速时转矩系数对比如图7所示。

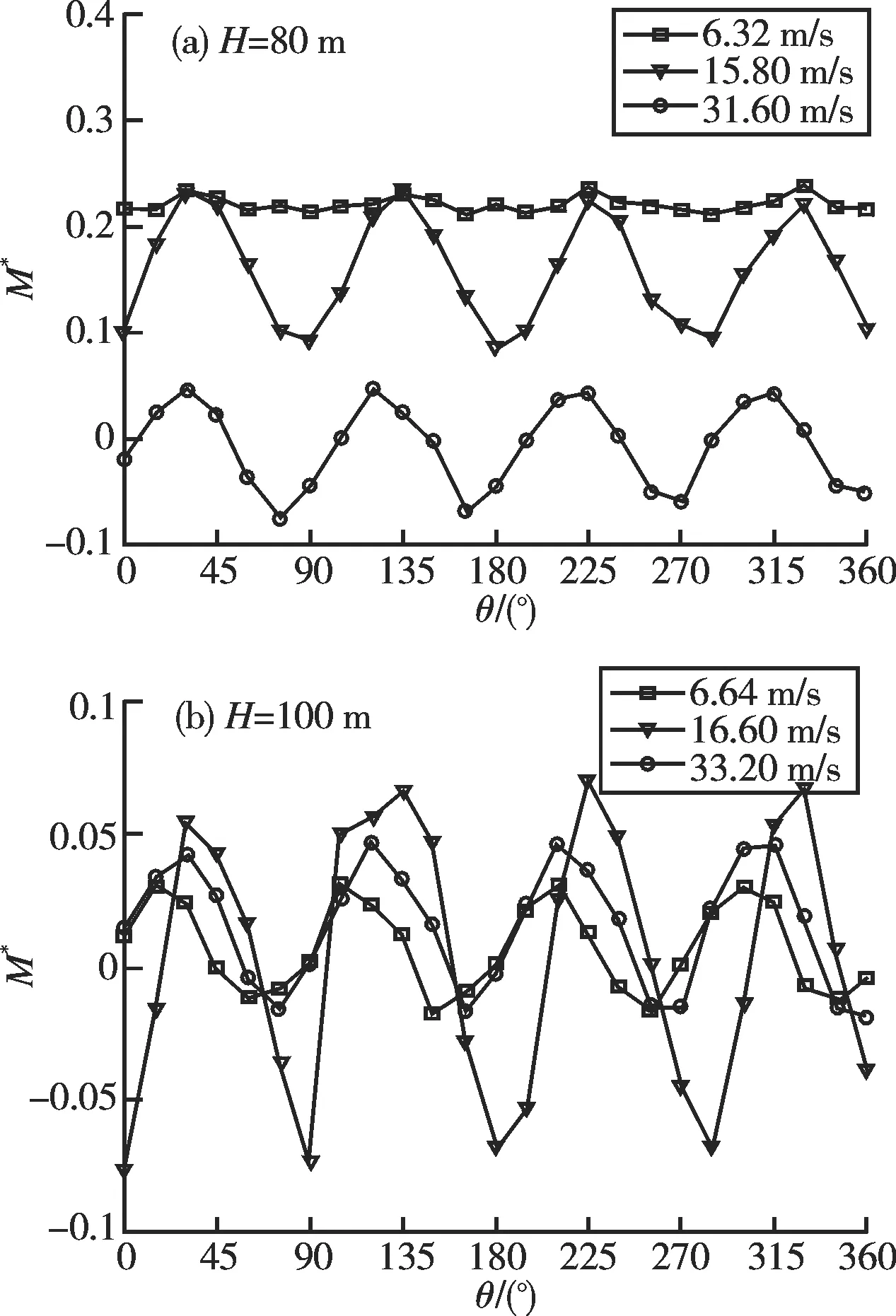
图7 #2风力机不同风速时的转矩系数Fig.7 Torque coefficient of #2 wind turbine at different wind speed

从图7可以看出：#2风力机，在H=80 m处时，随着风速的逐渐增大，转矩系数的平均值逐渐降低，但在H=100 m处，由于受到建筑顶部的分离流动的干扰，转矩系数并未出现随风速增大而降低的变化规律。

5.2 不同风速下速度等值线图对比分析

为了直观考察风力机与建筑一体化中风的运动特征，绘制了整个计算流场在不同风速作用下的等值线，如图8所示。

图8 不同风速速度等值线图Fig.8 Contour diagram for different wind speed

从速度等值线图可以看出，越靠近建筑壁面，其尾流风速越低，随着尾流远离建筑,尾流速度逐渐接近来流风速。这主要是由于尾流和自由气流之间的风速梯度引起的附加的切变湍流有助于周边气流与尾流之间的动量转换。因此，尾流和自由气流开始混合，混合区域向尾流中心扩散，最终逐渐消除了尾流中的速度的差异，直到在下游远处完全恢复为止。

对比几种不同来流风速下的速度等值线图可看出，随着风速的逐渐增加，尾流扩散区的长度逐渐增大；扩散区的长度增加的趋势上升；尾流扩散中心的最小尾流速度也越大。

4.3 不同来流时涡量图对比分析

在风力机与建筑一体化结构中，速度场的旋度与单纯只有建筑时是不同的，为了表征风在此结构中的旋涡场的旋涡流动，本次研究中，绘制了不同风速时流场中的涡量图，如图9所示。

通过对不同来流风速时涡量图分析可看出，在流场稳定后，建筑物后开始有序地出现多尺度、多形态的旋涡，即著名的卡门涡街。

从尾流局部放大图中可以清晰看到绕流分离后所产生的主涡和次涡，主涡即是建筑后面的大涡，次涡是指在建筑和主涡之间的小涡，次涡的尺寸明显比主涡的尺寸小很多，次涡通常被主涡压扁黏附在建筑的表面，从而体现出建筑钝体绕流的分离、在附、到再分离的特征。其次，从局部涡量图分析来看，在建筑削角处也有旋涡存在，这种旋涡的存在是凹角壁面处风压为负压的主要原因。

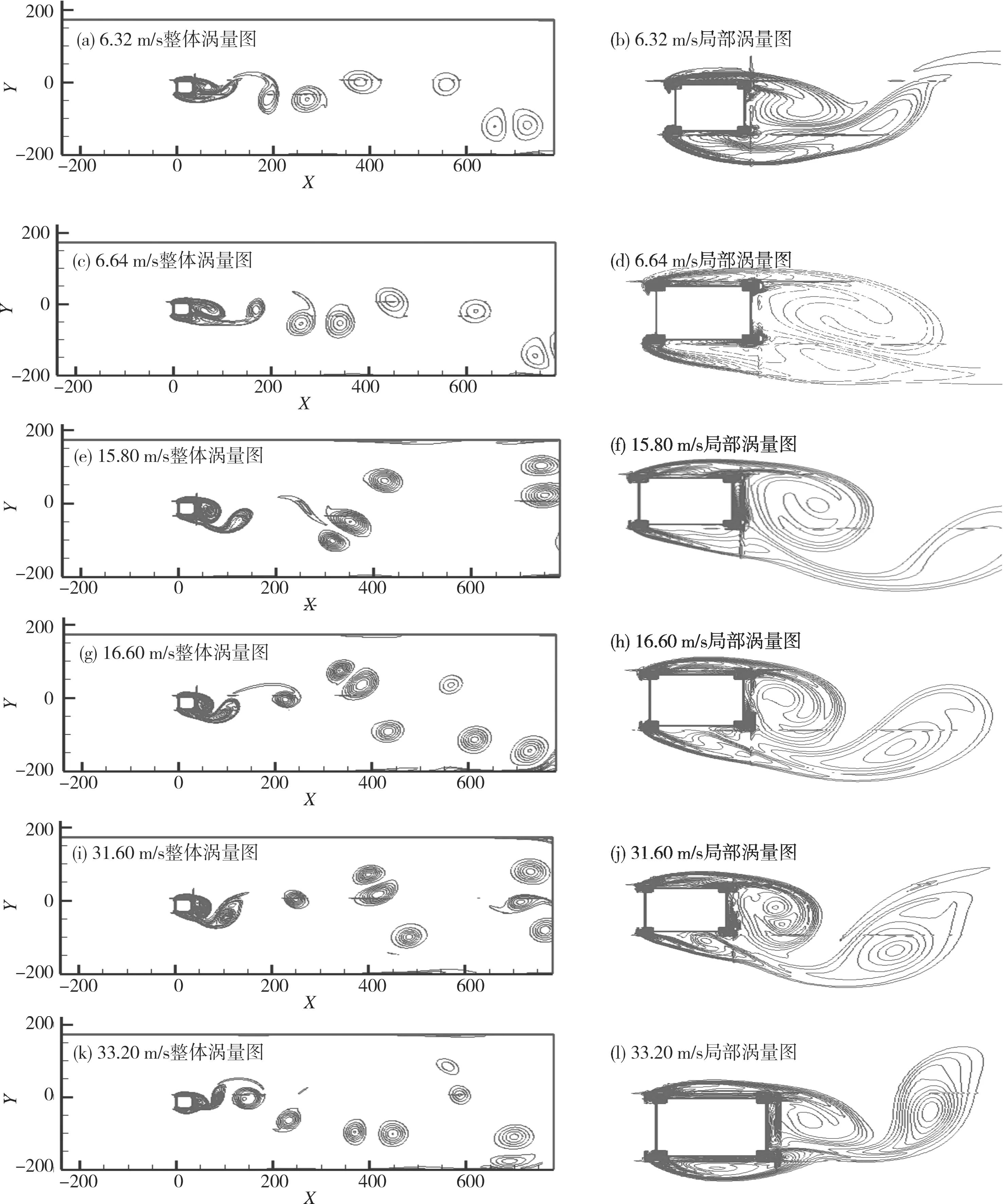
图9 不同风速下整体及局部涡量分布图 Fig. 9 Distribution diagram of overall and local vorticity at different wind speed

5 结论

通过对风力机与建筑一体化二维模型在不同风速下的动态研究，得到了相应的转矩系数，并对流场的速度分布和涡量分布进行了对比，得出主要结论如下： (1) 不同风速时，各风力机转矩系数按周期性变化。对#1风力机，当叶片的转角θ旋转到45°～75°，135°～165°，225°～255°及315°～345°时，转矩系数最大，其值约为0.37～0.41；而当叶片旋转到90°～120°，180°～210°，270°～300°时，转矩系数最小，其值约为0.10～0.15。对于#2风力机，风速为6.32 m/s时，转矩系数基本上维持在0.22左右，但随着风速的增大，其转矩系数出现正负交替的变化趋势，当叶片的转角θ旋转到0°～30°，90°～120°,190°～210°,285°～315°时为正值；在45°～75°,135°～165°,225°～255°时为负值。其值的变化范围在 5%之间。 (2) #1风力机在不同的高度处，转矩系数最大值均出现在来流风速最大时，其值为0.41；最小值则出现在来流为15.8 m/s和16.6 m/s 时，其值为0.10。#2风力机，在H=80 m处时，随着风速的逐渐增大，转矩系数的平均值逐渐降低；但在H=100 m处，由于受到建筑顶部的分离流动的干扰，转矩系数并未出现随风速增大而降低的变化规律。 (3) 随着尾流远离建筑,尾流速度逐渐接近来流风速，越靠近建筑壁面，其尾流风速越低；风速增加，尾流扩散区的长度逐渐增大；尾流扩散中心的最小尾流速度越大。 (4) 流场稳定后，建筑物后开始有序出现多尺度、多形态的卡门涡街。

[1] SALAMEH Z, NANDU C V. Overview of Building Integrated Wind Energy Conversion Systems [A]. Power and Energy Society General Meeting, 2010 IEEE, 25-29 July 2010 [C] IEEE press.

[2] ZHU Zheng-lin, WANG Hong-yan, BI Xiao-long. Study and Application of the Wind Power on the Tall Building Rooftops in Large Cities [A]. Materials for Renewable Energy & Environment (ICMREE), 2011 International Conference, 2011 IEEE, Shanghai, 20-22 May 2011 [C]. Shanghai: IEEE press: 566-569.

[3] ABOHELA I, HAMZA N, DUDEK S. Effect of roof shape, wind direction, building height and urban configuration on the energy yield and positioning of roof mounted wind turbines[J].Renewable Energy,2013(50) :1106-1118.

[4] PAULIDES J J H, ENCICA L, JANSEN J W. Small-scale Urban Venturi Wind Turbine: Direct-Drive Generator[A]. Electric Machines and Drives Conference, 2009. IEMDC '09. IEEE International, Miami, May 3-6,2009 [C].USA: IEEE press: 1368-1373.

[5] SHARPE T, PROVEN G. Crossflex: Concept and early development of a true building integrated wind turbine [J]. Energy and Buildings, 2010(42): 2365-2375.

[6] KIM Y C, KANDA J. Wind pressures on tapered and set-back tall buildings[J]. Journal of Fluids and Structures,2013(39):306-321.

[7] ROSA L, TOMASINI G. Wind-induced dynamics and loads in a prismatic slender building: A modal approach based on unsteady pressure measurements[J]. Journal of Wind Engineering and Industrial Aerodynamics,2012,7(108):118-130.

[8] YANG Yi, GU Ming. New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics,2009,(97):88-95.

[9] HUANG Sheng-hong, LI Q S, XU Sheng-li. Numerical evaluation of wind effects on a tall steel building by CFD[J]. Journal of Constructional Steel Research, 2007(63) :612-627.

[10] 王企鲲.导流型垂直轴风力机内部流场数值模拟中若干问题的探讨[J].机械工程学报，2011，4(47)：147-154.

[11] 贺德馨.风工程与工业空气动力学[M].北京：国防工业出版社，2006.

The Dynamic Numerical Analysis of Two-dimensional Model of High Building Integrated with Vertical Axis Wind Turbine

PENG Wei1, ZHANG Zu-peng1, ZHANG Wei1，2, CHEN Guo-ping1

(1.SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan,China; 2.UniversityofScienceandTechnologyofChina,Hefei230027,Anhui,China)

This paper used the standardk-εturbulence method and sliding mesh technique to research the two-dimensional model of building integrated with wind turbine under different wind speed, and the torque coefficient of wind turbine and physical properties of whole flow field were analyzed without considering the impact of the connection between building and wind turbine and the speed loss of blade. The results show that: Under different wind speed, the maximum value of torque coefficient of wind turbine on the windward side is 0.41, the minimum value is 0.10; the torque coefficient of leeward side maximum value is 0.27, the minimum value is 0.17.

The standardk-εturbulence simulation method； Vertical axis wind turbine； High rise building； The load of Wind； Torque coefficient

2015-02-07

彭伟，男，硕士研究生。通讯作者：陈国平(1962—),男，教授，研究方向为结构风工程。E-mail：guopingchen2002@163.com

TU311.3

A

1671-8755(2015)02-0061-08