一维非散度椭圆方程解的二阶导数的高阶可积性

白晋彦

(晋中学院 数学学院,山西 晋中 030600)

一维非散度椭圆方程解的二阶导数的高阶可积性

白晋彦

(晋中学院 数学学院,山西 晋中 030600)

一维;非散度椭圆方程;低阶项;高阶可积性

0 引言

很多学者已经对椭圆方程解的高阶可积性问题进行了研究.Companato在文[1]中建立了解的二阶导数的高阶可积性,同样的方法被运用到散度椭圆方程后得到同样的结果[2].M.Franciosi和G.Moscariello在文[3]中,证明了如果函数f满足反向积分不等式, 那么非增重排函数f满足同样的不等式, 并且作为反向积分不等式的应用, 在一维情况下给出了高阶可积性的简单证明.T.Radice对不带低阶项的非散度椭圆方程解的二阶导数的高阶可积性进行了研究[4].本文的主要目的是对一维情况下的带低阶项的非散度椭圆方程低阶项系数做了处理,得出了带低阶项的非散度椭圆方程解得二阶导数的高阶可积性结果.

考虑算子

(1)

这里主要研究方程

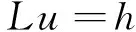
(2)

解的二阶导数的高阶可积性.假设系数满足下面的条件:

(H1) 1≤a(x)≤K.

(3)

(4)

(5)

本文的主要结论是:

(6)

这里2I与I是同一中心,并且长是I的两倍.

下边的L2估计是证明定理1的核心.

(7)

这里|uxx|∈L2(Ω)并且h∈L2(Ω).

这里常数C≥0依赖于对我们的研究无关紧要的常数, 文中出现的C可能不是同一个常数.

1 预备知识

引理1[4]设u∈W2,2(Ω), 对任意的ε>0, 我们有

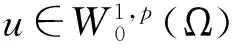
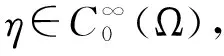
上述引理可根据文献[4]中的方法很容易验证.

引理4(高阶Poincaré不等式,见[6]) 若u∈W2,s(Ω),则

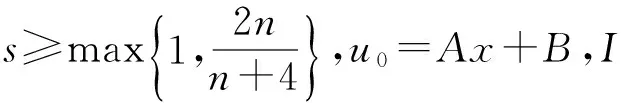
引理5(反向Höider不等式,见[5])设Ω是R中的有界开集,g∈Lq(Ω),q>1, 若对任意区间I⊂2I⊂⊂Ω,

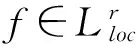
以上引理均可根据文献中的方法类似推广到一维情形,容易验证结论仍然成立.

2 定理2的证明

根据假设(H1)以及方程(2),我们有

不等式两边同时在Ω上积分,并利用Hölder不等式,则有

即

所以,

运用插值不等式,可得

故

即

3 定理1的证明

(8)

根据定理2和假设(H1),有

由于

即

(9)

注意到v=φu,那么

并且有

(10)

联立(9)和(10)即得

记η=|φx|,运用引理3和|ηx|=|φxx|,我们有

令φ=ψ2则

因此有

利用不等式(a+b)2≤2(a2+b2)我们得到

定理证明:

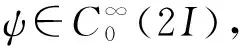
用此处的ψ代入(8),得到

即

运用高阶Poincaré不等式

据反向Höider不等式得

[1] CAMPANATO S.Un risultato relativeo ad equazioni ellittiche del secondo ordine di tipo non variazionale[J].Ann.Scuola Norm.Sup.Pisa,1967,21(4):701-707

[2] MEYERS N G. AnLpestimate for the gradient of solutions of second order elliptic divergence equations[J].Ann.Sc.Norm.Sup.Pisa,1963,17(3):189-206

[3] FRANCIOSI M,Moscariello G.Higher integrability results[J].Manuscripta Math.,1985,52(1-3):151-170

[4] RADICE T. A higher integrability result for nondivergence elliptic equations[J].Annali di Matematica,2008,187(1):93-103

[5] WU Z Q,YI J X,WANG C P.An introduction to elliptic and parabolic equations[M].Beijing:Science Press,2003:12-16

[6] COHN W S,LU G Z,WANG P Y.Sub-elliptic global high order poincaré inequalities in stratified Lie groups and applications[J].Journal of Functional Analysis,2007,249(2):393-424

[7] AUBIN J P.Applied functional analysis[M].Paris:University of Paris-Dauphine,1979:153

Higher Integrability Result for Solutions to Nondivergence Elliptic Equations in the One Dimensional

BAI Jinyan

(Mathematics School of Jinzhong University,Jinzhong 030600, China)

onedimensional;nondivergenceellipticequation;loworderterms;higherintegrability

2015-10-16

白晋彦(1987-)，女,山西朔州人,硕士,晋中学院数学学院助教,主要从事偏微分方程的研究.

1672-2027(2015)04-0008-04

O175.25

A