导弹目标RCS计算的高阶有限元-边界积分方法
赵 蕾
(南京工业职业技术学院,江苏 南京 210023)
导弹目标RCS计算的高阶有限元-边界积分方法
赵蕾
(南京工业职业技术学院,江苏 南京 210023)
摘要:导弹目标的RCS对于目标探测识别及导弹的隐身设计都有重要的意义。提出了一种基于高阶叠层基函数的高阶有限元-边界积分(FE-BI)方法,用来分析复杂电大尺寸导弹目标的电磁散射特性。该方法在有限元部分和边界部分都使用高阶叠层基函数,通过具体的算例可看出使用这种高阶叠层基函数的FE-BI方法具有更优的矩阵性态。同时比较了高阶FE-BI方法和低阶FE-BI方法,可看出高阶FE-BI方法具有更高的精确性,可有效地减小所分析问题需要的未知量,减小内存消耗。
关键词:高阶叠层基函数;有限元-边界积分法;导弹目标RCS
0引言
有限元法是近似求解数理边值问题的一种数值方法,它对场域的剖分具有很大的灵活性,因此,对不规则、非均匀的物体具有广泛的适用性,而且形成的矩阵为稀疏矩阵,可以利用这一特点来快速求解含大未知量的稀疏矩阵方程。但有限元在分析开域问题时由于区域的无限大,有限元剖分时将有无穷多个节点,所形成的矩阵方程将很难求解。多年来对于开域问题的研究概括起来主要有[1-3]:第一类是利用吸收边界条件或完全匹配层技术将无限大空间截断,使原问题限制在被研究物体周围一个有限的范围内,然后采用有限元进行分析;第二类是应用矩量法或边界积分方程来处理被研究物体以外的无限大空间。第一类方法缺点在于扩大了研究区域,产生了较多的节点数,特别是吸收边界的形状以及其与散射体间的距离对于解得精度有很大的影响。第二类方法精度较高,所产生的节点数较少,但生成的是部分稀疏、部分满秩阵,如果能够快速求解该方程,则该方法有着较好的应用前景,特别是对于电尺寸较大的散射体。
本文在已有文献工作的基础上,将一种高阶叠层基函数运用到高阶有限元-边界积分(FE-BI)中,并应用该高阶FE-BI法分析复杂目标的电磁散射特性。对散射体内外区域分别应用高阶有限元和高阶边界积分法进行分析。然后通过场的边界连续性进行耦合,形成待求矩阵方程组,求解该方程组。通过具体的数值算例可看出,使用这种高阶叠层基函数的FE-BI方法具有更优的矩阵性态,并且与低阶FE-BI相比,高阶FE-BI方法有着更高的计算精度性、收敛速度和更高的计算效率。
1 理论分析1.1 FE-BE法基本原理
图1所示为一个涂层体,以涂层体最外层的边界面Se将整个区域分成两个区域,面内的体V为介质层,面外为自由空间,或无限大的背景空间。平面波从外照射到这一涂层体上,Si是金属闭合表面,因此其内部结构可以不必考虑。在分析时,将区域V内的场用有限元法建立方程,对于外部自由空间区域中的场,用矩量法建立方程,然后让这两部分的场在边界上满足不连续条件,建立一个完整的可以求解的方程。

图1 任意目标在平面波照射下的示意图
根据这一思路,可以得出相应部分的公式如下:
在区域V内电场满足矢量波动方程:

(1)

将式(1)写成变分的形式,可得:
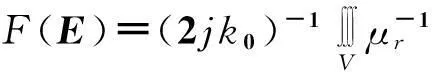

(2)
由于式(2)中H只在表面出现,式(2)可以转换为:


(3)
将E和JS分别用基函数展开:

对上述泛函求变分,可得:
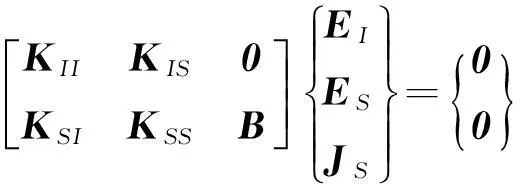
(4)
根据等效原理,边界Se上等效面电流JS产生的散射场满足混合边界积分方程, 本文采用TE+NH型混合场积分方程,有如下形式:

式中,L和K算子的具体定义见参考文献[4~5],对上述方程组使用高阶基函数作为基函数与测试基函数可得一组线性方程,即:

(5)
式中,P和Q的矩阵元素及b向量的详细表达式在文献[4~5]中已详细给出。
综合式(4)和式(5)可获得进行求解的矩阵方程的形式:
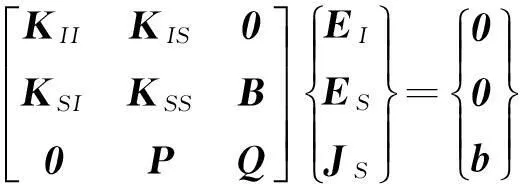
(6)
1.2 新型高阶叠层基函数
根据参考文献[6]中关于叠层基函数的构造方式,可推导出应用在有限元部分的旋度共形高阶叠层基函数和应用在边界部分的散度共形高阶叠层基函数。首先推导有限元部分的旋度共形高阶叠层基函数,具体如下:
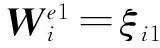


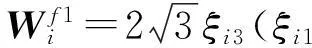







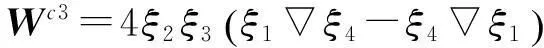
(7)
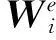
在应用有限元-边界积分方程时,在有限元部分和边界部分都使用1.5阶的高阶叠层型基函数,边界面上的散度共形基函数和有限元内部的旋度共形基函数满足关系:

(8)

2数值算例
如图2所示的具有复杂几何外形的导弹模型,模型x、y、z方向尺寸分别为2.5m、1.0m、3.3m, 导弹的材料为纯金属。设定雷达工作频率为300MHz,雷达照射波从导弹头方向垂直入射,采用本文提出的方法来分析该导弹目标的双站RCS。迭代算法收敛精度为1.0e-03。在导弹模型表面包裹一层0.1m的空气层用来设置有限元边界,利用ANSYS软件对空气层和导弹表面进行网格划分,得到的四面体数为9573,三角形数为3740,从而分别得到有限元未知量63814,边界积分未知量18700。利用本文提出的高阶FE-BI算法形成矩阵方程,采用迭代算法求解得到散射电场和感应电流的未知展开系数。当雷达照射波分别为垂直极化入射和水平极化入射时,仿真计算得到的导弹目标同极化雷达散射回波如图3所示。从所给出的结果可看出,高阶FE-BI仿真得到的结果和商业软件FEKO的结果都吻合得很好,说明了本文提出算法的正确性。
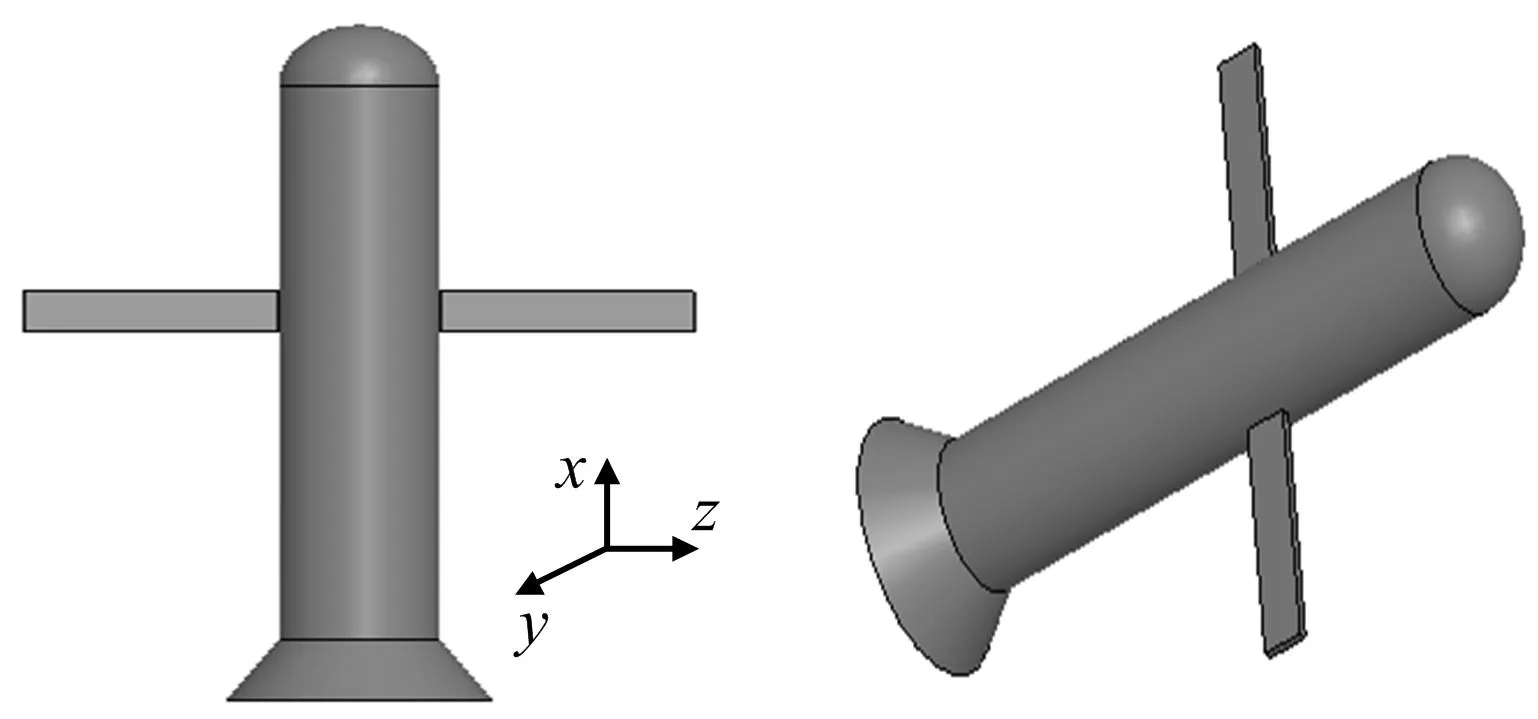
图2 导弹模型示意图

图3 导弹目标的雷达散射截面(RCS)
本文的高阶FE-BI方法和文献[7]中提出的FE-BI方法在计算该算例时使用的求解未知量数目和求解时间的比较,如表1所示。数值结果表明本文提出的高阶FE-BI方法需要的求解未知量和求解时间更少,收敛性态更优,证明了本文算法的有效性。

表1 不同FE-BI方法的未知量数目和求解时间比较
3结束语
由导弹目标RCS的仿真结果可以看出,对于该种外形的导弹目标,迎头方向的散射回波最强。在雷达照射波水平极化时,产生的雷达回波散射中心多于垂直极化照射波产生的散射回波,因此采用天线水平极化方式的雷达更利于对导弹目标的探测。本文提出了一种基于高阶叠层矢量基函数的高阶FE-BI方法,用来精确求解具有任意复杂外形的导弹目标的RCS,数值算例证明了本文提出方法的有效性。■
参考文献:
[1]Dangelo J, Mayergoyz ID. On the use of absorbing boundary conditions for RF scattering problems[J]. IEEE Trans. on Magnet, 1989,25(7):3040-3042.
[2]Andreas CC, Lee R. The moment method for two dimensional electromagnetic scattering[J]. IEEE Trans. on Antennas and Propagat., 1990,38(9):1429-1437.
[3]Jin JM. Simple moment method program for computing scattering from complex cylindrical obstacles[J]. IEE Proc. H, 1989,136(8):321-329.
[4]樊振宏.电磁散射分析中的快速算法[D].南京:南京理工大学,2006.
[5]盛新庆.计算电磁学要论[M].北京:科学出版社,2004.
[6]Graglia RD, Peterson AF, Andriulli FP. Curl-conforming hierarchical vector bases for triangles and tetrahedral[J]. IEEE Trans. on Antennas and Propagat., 2011,59(3):950-959.
[7]Botha MM, Jin JM. On the variational formulation of hybrid finite element-boundary integral techniques for electromagnetic analysis[J]. IEEE Trans. on Antennas and Propagat., 2004,52(11):3037-3047.
Higher order finite element-boundary integration method for RCS
computation of missile target
Zhao Lei
(Nanjing Institute of Industry Technology,Nanjing 210023,Jiangsu,China)
Abstract:The radar cross section (RCS) of missile target has great significance to the target detection and recognition, and the stealthy design of missile target. The higher order finite element-boundary integration (FE-BI) based method is proposed for analyzing the electromagnetic scattering characteristics of complex electrical large missile target. The higher order hierarchical basis function is used both in the FE region and BI region. It can be found from the numerical example that the convergence properties of FE-BI matrix is improved by using the higher order bases. More accurate results can be obtained by the higher order FE-BI method, which compared with the general method. The unknown number and the memory cost also can be reduced efficiently.
Key words:higher order hierarchical basis function;FE-BI method;RCS of missile target
中图分类号:TJ765.4+1;TN974
文献标识码:A
作者简介:赵蕾(1978-),女,高工,硕士,主要研究方向为航天电子对抗。
收稿日期:2015-09-26;2015-11-05修回。

