一种直线插补算法及其在机器人中的应用研究*

李进文，何素梅，吴海彬

(福州大学机械工程与自动化学院，福建福州350108)

0 引 言

工业机器人在搬运、码垛、焊接、上下料等场合的应用越来越普遍，技术越来越成熟。很多经济型工业机器人普遍选用通用的运动控制型PLC 作为机器人控制器。运动控制型PLC 有专门的高速脉冲输出通道，可以通过对电机驱动器输出脉冲实现单轴的运动控制。通常情况下，当机器人需要按照规划的直线或曲线轨迹进行运动时，机器人控制器需要具备插补功能。在轨迹跟踪精度要求不是很高的前提下，可以用直线插补替代圆弧插补实现曲线轨迹的运动，因此，直线插补是机器人实现插补运动最基本最重要的方法。有些运动控制型PLC 只提供单轴或多轴高速脉冲输出功能，无插补指令;少数PLC 提供直线插补指令，但PLC 自带的插补指令，其插补轴数一般为两轴，并且这两轴均为直线运动关节，即两轴间插补的脉冲比例固定不变。而对于直线运动关节和转动关节、或转动关节与转动关节之间的插补，这样的插补指令并不能使用。

针对以上问题，有研究者开发了一套直线插补或者圆弧插补程序［1-4］，但所用方法并没有充分利用PLC内置的脉冲输出指令，插补脉冲频率低、插补实时性差。通过采用专用的定位模块也可以实现直线插补［5］，虽然提高了插补脉冲频率，但大大增加了系统成本。有相关文献提出利用PLC 本身内置的脉冲输出指令［6-7］，开发高速直线插补程序，但是其只适用于插补轴为两轴、插补的脉冲比例固定不变的场合。

针对以上问题，本研究提出了一种基于等时间间隔直线插补算法，该算法可以在任意结构形式的工业机器人上实现任意轴数的空间直线插补，适用于任意低成本的机器人控制器。

1 直线插补算法

基于等时间间隔的空间直线插补，就是在一个确定的时间间隔(也称为插补周期)ΔT 内完成一次插补计算，为各坐标方向的运动提供一组数据。机器人控制器按照插补计算得到的数据，控制机器人各关节同时完成一次微小运动，从而使机器人执行器末端经过规划的插补点［8-10］。

1．1 插补原理

机器人末端执行器在笛卡尔坐标系中的描述，包括位置描述与姿态描述，因此其插补算法中也包括位置插补与姿态插补。姿态插补一般采取线性方式，即把末端执行器在曲线上的终点和起点的方位差均匀地分配到插补的每一步，算法简单，本研究不作讨论。位置插补，就是求出在一个插补周期内，机器人末端执行器从当前位置(Xi，Yi，Zi)沿插补直线方向截取线段长ΔL(ΔL 取决于插补速度V、加减速时间Ta)后，所到达的下一个插补点位置(Xi+1，Yi+1，Zi+1)。

1．2 插补递推公式

已知空间插补直线的起点坐标P1(x1，y1，z1)和终点坐标P2(x2，y2，z2)，其中P1，P2为相对于基座坐标系的坐标点，可以通过示教得到。设V 为沿插补直线方向的运动速度，ΔT 为插补周期，Ta为插补运动的加减速时间。

基于此可以求出直线轨迹长度:

(1)插补直线的长度L:

(2)插补总步数N:不考虑加减速的情况，可得理论插补步数N0:

实际上，考虑到机械臂的惯性以及高速脉冲输出通道对初始脉冲频率的限制，应该在插补直线的首尾分别设置加、减速段，因此实际的插补总步数应大于理论插补步数。由插补运动的加减速时间Ta可求得笛卡尔坐标系下的加减速度a:

加减速段的插补步数Na:

从而，得到实际插补总步数N:

(3)确定插补点与插补起点的距离Si:根据加减速特性的相关参数可计算出任意插补点Ni(i=1～N)与插补起点P1的距离Si:

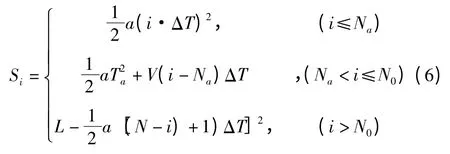
(4)确定插补点Ni的坐标:插补起点P1(x1，y1，z1)与Si在笛卡尔坐标系三坐标轴方向上的分量叠加，即可得到各插补点在笛卡尔坐标系下的坐标(Xi，Yi，Zi):

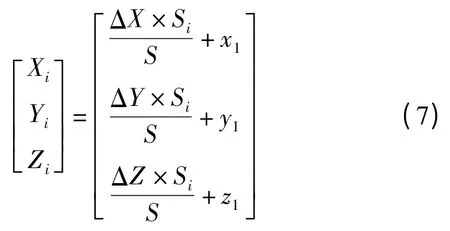
式中:ΔX=x2－x1;ΔY=y2－y1;ΔZ=z2－z1。

由插补递推过程知，插补点总在插补直线上，算法没有累积误差。求得各插补点的坐标后，再通过机器人运动学逆解，即可求得各插补点对应的关节变量。

对于不同的控制器，特别是PLC，由于存储空间有限，其所能存储的插补点数据是有限的。上述算法中插补周期ΔT 可以根据控制器的存储空间以及插补直线的数量进行选择，从而可以降低对控制器的性能要求。

2 插补算法的应用

以实验室自行研发的四关节冲床上下料机器人为研究平台，探讨并验证上述算法。该机器人结构示意图和实物图如图1 所示。

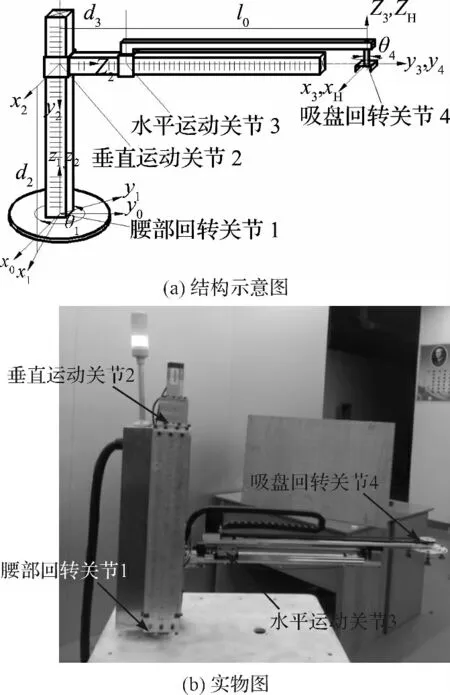
图1 四关节冲床上下料机器人

利用D-H 法建立机器人坐标系，可得到机器人末端执行器的正运动学方程为:

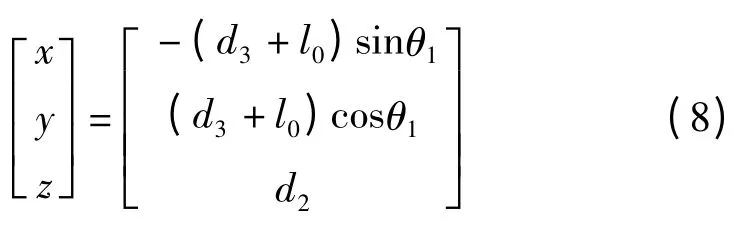
逆运动学方程为:

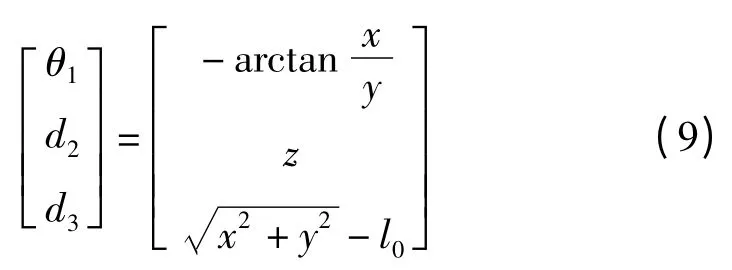
由于关节4 的运动只对机器人末端执行器的姿态产生影响，这里不予讨论。

2．1 插补算法在PLC 上的实现

机器人控制器选用松下FP-X C60T 运动控制型PLC，其内置两个频率范围1．5 Hz～100 kHz 和两个频率范围1．5 Hz～20 kHz 的脉冲输出通道，具有强大的浮点和三角函数运算功能，非常适合算法编程［11］。PLC 上的直线插补程序流程图如图2 所示。以下通过流程图2 重点说明插补算法在PLC 上的实现。

插补程序采用绝对值式脉冲输出。插补运动开始前先建立数据表，数据表结构如图3 所示。数据表由连续的双字组成，分别是控制代码、频率、目标脉冲值及脉冲输出停止标志组成。其中控制代码以位为单位使用，包括占空比、频率范围选择、脉冲输出模式、脉冲输出方式等。

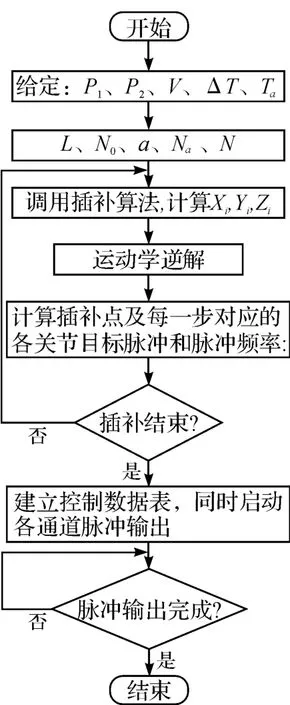
图2 PLC 上的直线插补程序流程图

图3 PLC 的数据表结构

本研究在建立数据表前，先求出只需计算1 次的初始数据，为计算插补点做准备。之后，根据插补步数选择加速段—匀速段—减速段距离，获得插补点坐标。通过机器人运动学逆解，即可求得各插补点对应的关节变量，进而求得插补点及每一步对应的各关节目标脉冲和脉冲频率。控制数据表每一组频率及目标脉冲值对应一个插补点。插补计算结束时，建立运动控制数据表，并同时启动各通道脉冲输出，直到所插补直线脉冲输出完成，结束插补程序。

上述插补程序约800 步，PLC 平均扫描时间为25 ms。

2．2 误差的定性分析

2．2．1 插补程序造成的误差

由于机器人结构的关系，求得各插补点坐标进而求取各插补点及每一步对应的各关节目标脉冲和脉冲频率时，可能得到某两点之间的目标脉冲值相等的情况(即［S+2(N+1)］=［S+2(N +3)］)。此时，若不对目标脉冲值进行修正，会造成实际输出脉冲数量与指定脉冲数值不同。本研究所采取的修正方法为:当出现上一插补点的目标脉冲值与当前插补点的目标脉冲值相等时，将当前插补点的目标脉冲值加1，使其与上一插补点的目标脉冲值不一致。设当前插补点目标脉冲值修正后对应的坐标为N'i(X'i，Y'i，Z'i)，修正后各关节变量与修正前各关节变量差值Δθ1、Δd2、Δd3(即Δθ1=δ1，Δd2=δ2，Δd3=δ3)。此时，插补点定位误差δi:

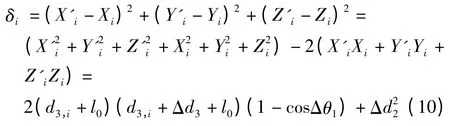
笔者所研究的机器人，各关节脉冲当量分别为δ1=0．002 5 rad、δ2=0．025 mm、δ3=0．013 mm，将上述数据带代入式(10)，得到修正后插补点定位误差δi≈6．25 ×10－4mm，可以满足实际使用。

2．2．2 最低脉冲频率造成的误差

由于PLC 硬件上最低脉冲频率的限制，求得的两插补点间对应的各关节脉冲频率可能低于允许最低脉冲频率，此时PLC 会以最低脉冲频率进行脉冲输出，这样，在某个插补点的运动上一个关节先于另一个关节完成脉冲输出，造成插补误差。最低脉冲频率造成的误差如图4 所示。粗实线是理想的插补直线，虚线是为满足最低脉冲频率限制要求得到的实际插补直线。

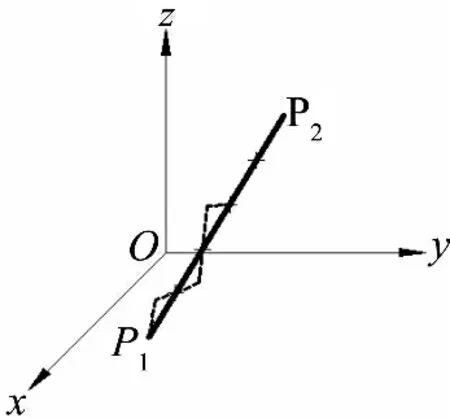
图4 最低脉冲频率造成的误差

3 实验及结果分析

为验证插补算法在自行研发的四关节冲床上下料机器人的应用效果，本研究设计实验如下:机器人以起点P1(－926． 57，535． 03，50)，终点P2(－1 144．43，659．60，186．60)做直线插补，其中:V =240 mm/s，ΔT =50 ms、Ta=200 ms，实际插补轨迹如图5 所示。由于机器人在运动过程中、特别是在加减速阶段存在一定的抖动情况，以及传动系统少许的间隙，致使机器人在实际运动过程中末端操作器的轨迹偏差还会更大一些。

图5 插补直线的实际轨迹

插补过程中，每10 ms 采样一次PLC 各脉冲通道输出的绝对脉冲值，结合机器人结构，得到插补直线采样点的空间坐标如图6 所示。从图6 可以看出，空间上插补直线可以比较好的跟踪理论直线轨迹。

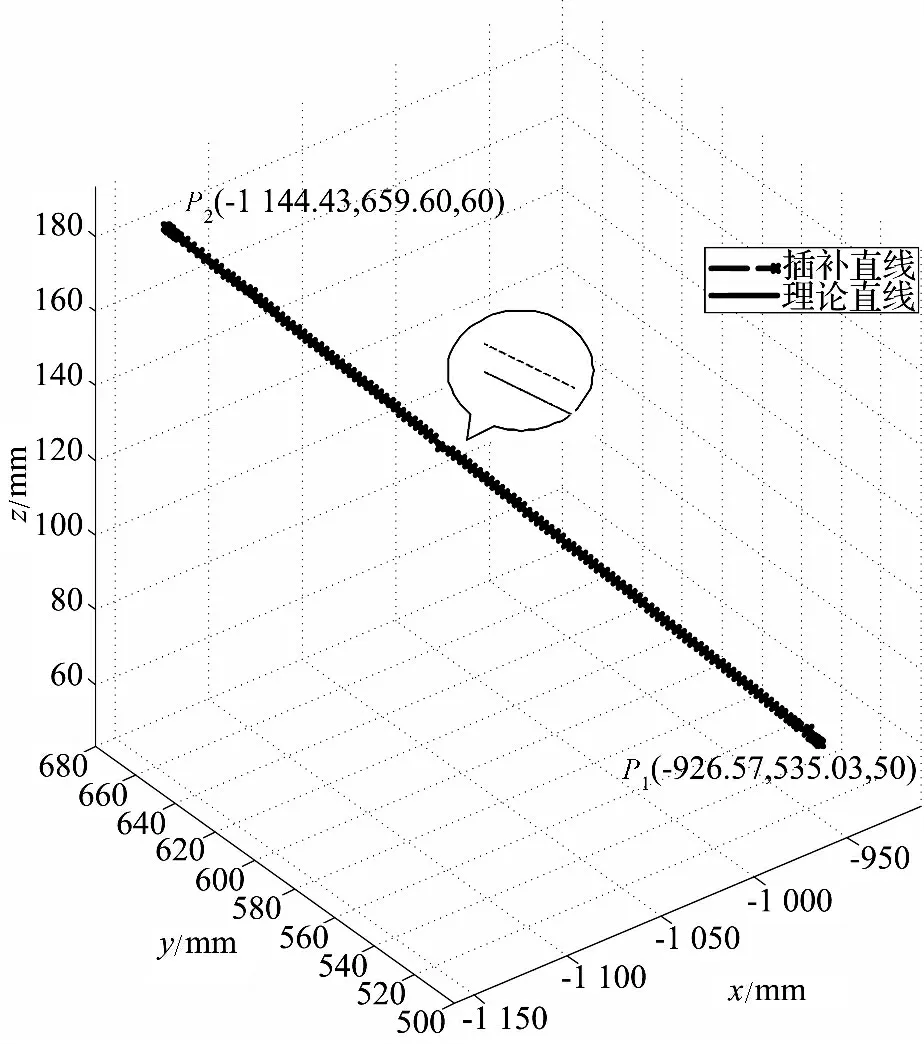
图6 插补直线与理论直线的空间重合度

为进一步定量分析插补直线对理论直线的跟踪精度，以插补直线为横坐标，插补直线与理论直线对应采样点的距离为纵坐标，作图得到插补直线对理论直线的跟踪精度如图7 所示。跟踪误差小于0．3 mm，满足机器人直线插补的精度要求。虽然插补直线不能与理论直线完全重合，但其基本与理论直线平行，如图6 中插补直线与理论直线的局部放大图所示。如果需要提高直线插补跟踪精度，则需要减小插补周期，增加插补点数，但这反而会提高对控制器的性能要求。

图7 插补直线对理论直线的跟踪精度

4 结束语

本研究针对工业机器人在笛卡尔坐标系中的空间直线轨迹规划问题，提出了一种基于等时间间隔的直线插补算法。该算法可以在任意结构形式的工业机器人上实现任意轴数的空间直线插补，对于有直线插补要求、但跟踪精度要求不高的应用场合，可以通过适当增加插补周期、减少插补点数的方法降低控制器的硬件配置，从而降低机器人系统成本。所述算法已成功应用在自行研发的四关节冲床上下料机器人上，实际应用表明了该直线插补算法的有效性，具有一定的应用价值。

今后将通过其他机器人平台来进一步验证提出的直线粗插补算法的有效性。同时，考虑到圆弧插补算法在机器人曲线轨迹规划中应用的普遍性，今后将进一步探讨圆弧插补算法及其在低配置控制器上的实现。

［1］张铁异，黄柄琼，卢福宁，等．基于松下电工FPl 型PLC 的直线插补程序设计［J］．装备制造技术，2007(10):68-70．

［2］黄菊生，龚庆寿，夏 平，等． 数控平台PLC 控制系统的开发［J］．机床与液压，2005(4):56-58．

［3］孙建仁．步进电机的PIE 控制系统设计［J］．机械研究与应用，2001(4):23-26．

［4］赵燕伟，朱双胜，卢 东，等．基于直线插补的字体边缘识别技术［J］．机电工程，2009，26(5):52-54．

［5］谭怀亮，刘 晓，贺再红．基于三菱PLC 的刨床数控系统［J］．机械与电子，1999(6):51-53．

［6］任善岩． PLC 直线插补方法的研究［J］． 机床与液压，2009，37(9):56-58．．

［7］叶伯生．计算机数控系统原理、编程与操作［M］．武汉:华中理工大学出版社，1999．

［8］金建新．机床CNC 系统中任意空间曲线的可控步长插补方法［J］．机械工程学报，2002(4):95-97．

［9］ADACHI H． Line interpolation apparatus and line interpolation method:U．S． Patent 6，636，267［P］．2003-10-21．

［10］席港港，赵庆志，王 军，等．传统逐点比较法直线插补方法的改进［J］．山东理工大学学报:自然科学版，2012，26(1):67-69．

［11］Matsushita Electric Works，Ltd．． FP Series Programming Manual［Z］．Matsushita Electric Works，Ltd．，2012．