恒温反应器温度场数值模拟与试验研究

麦云飞，李俊生

(上海理工大学机械工程学院，上海200093)

0 引 言

温度是影响医学检测结果的一个重要因素，过高或者过低的温度都会导致最后检测结果的不准确性，影响医生对病人身体状况的判断，得到错误的结论，延误病人的治疗，甚至发生医疗事故。因此，在医学检测过程中需要精确控制温度，使被测物始终处于所要求的温度环境中。全自动生物组织脱水机是一种全自动的医疗检测仪器，是一种控制、机械、医疗病理诊断、计算机技术等交叉学科产品。在脱水机工作过程中的，很多过程都要求在恒温的反应器中进行。所以精确控制反应器内部温度场的均匀性就对脱水后的切片质量影响很大［1］。按照要求，恒温反应器内液体的温度差应小于0．2 ℃。

实际的工程应用中，进行温度场的研究使用的基本都是数值模拟辅以试验验证的方法。2003年，日本的Matsunaga N．［2］提出quasi-decoupling 的温度控制方法，这种方法主要意思是通过控制加热片上的任意点的梯度温度和平均温度来抑制加热器的热相互作用，使加热片上的温度无论是在稳态或者瞬态情况下温度都是均匀的。2007年，日本的Nanno I．等人［3］在基于黑箱模型加热装置的传统控制有很强的干扰性的前提下，提出了使用温度差模型(TDM)的新型加热方法，对温度均匀性控制起到了一定的效果。2007年，日本的Nanno I．等人［4］在温度差模型的基础上又提出了使用二维加热片的加热方法提高温度的均匀性。上述研究主要通过对加热片功率的实时控制来优化温度场均匀性，本研究则是通过优化加热片的功率分布来提高温度场均匀性。

本研究利用Ansys 软件对恒温反应器的加热过程进行瞬态热分析，研究其温度场的均匀性。通过现场多种工况下的试验标定出准确度较高的有限元模型，再利用该模型进行数值模拟，辅以遗传算法进行优化计算，根据优化的方案进行现场试验，结果表明该方案可提高温度场的均匀性。

1 计算模型的建立

1．1 几何模型

组织脱水机中恒温反应器的外形尺寸为300 mm×215 mm ×140 mm，由很多零件组装而成，所以要先合理地简化模型，对恒温反应器的缸体、硅胶加热片、保温层、液路联接器、缸体内部的水等关键部件进行建模，清除恒温反应器上铰链，销钉，液位传感器，过滤片，脱水篮等对加热系统影响微小的部件，简化模型以IGS 格式导入ANSYS 中，恒温反应器几何模型如图1 所示。

图1 恒温反应器几何模型

1．2 有限元模型

恒温反应器装配模型先使用适应性强的二阶实体四面体单元对物理实体模型进行标准网格划分［5］，再对重点关注的部位，如硅胶加热片与反应缸缸体的接触面、缸体与液路联接器的接触面进行网格细化，最后得到恒温反应器的有限元模型如图2 所示，模型节点数为62 660，单元数为294 814。

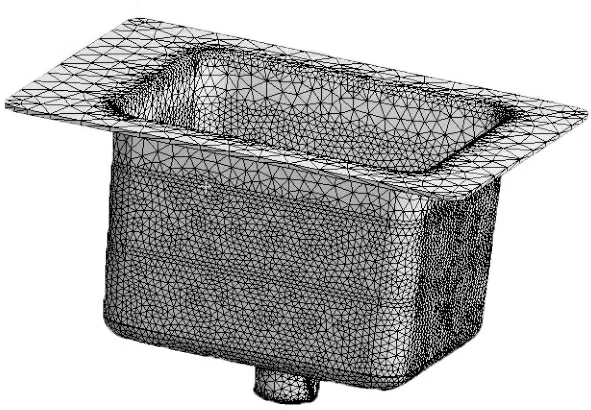
图2 恒温反应器有限元模型

反应缸缸体、液路联接器的材料为SUS 316L，加热片的材料为硅橡胶，缸体内的加热液体为水，周围介质为空气。钢、硅橡胶、水的热物性参数如表1 所示。

表1 材料热物性参数表

1．3 传热模型

恒温反应器加热系统结构的传热示意图如图3 所示。由于硅胶加热片是由外部的PID 控制器控制，控制器根据反应缸表面采集的温度来控制加热片电源的开启与关闭，可将其定义为外加可控温度场。

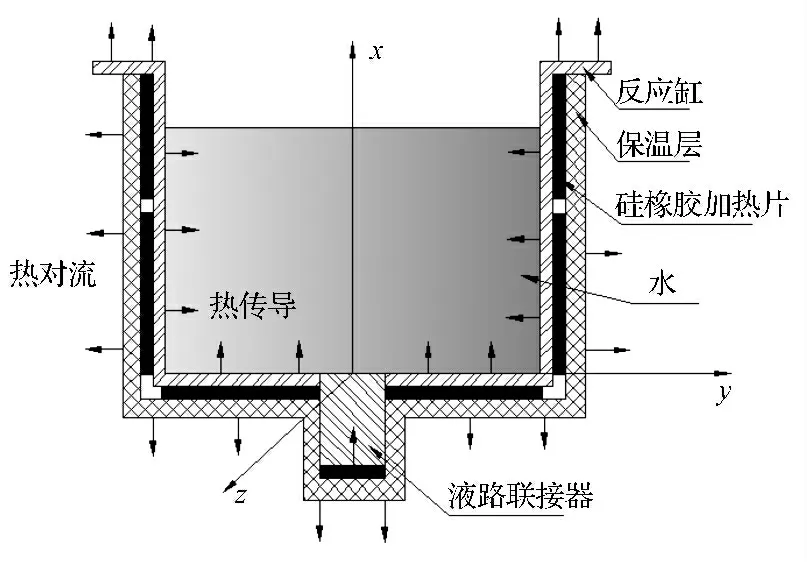
图3 传热示意图

根据傅里叶方程，恒温反应器外加可控温度场三维瞬态导热方程为:

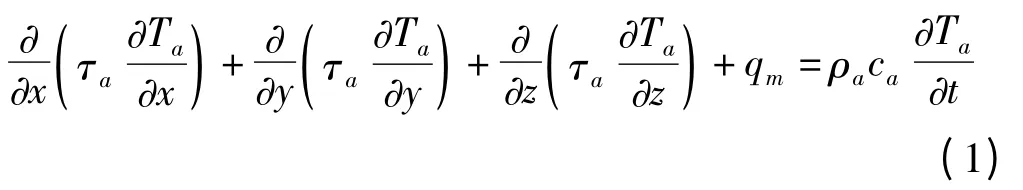
式中:Ta—恒温反应器内部的任意一点的瞬态温度场;x，y，z—坐标分量;τa—水的热导率;ρa—恒温反应器内部水的密度;ca—恒温反应器内部水的比热容;qm—外加热源项。

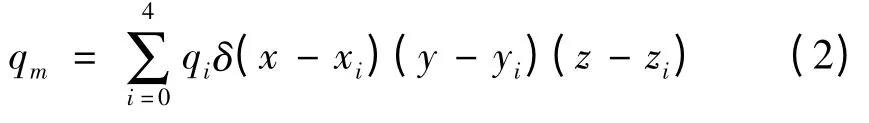
式中:qi—i 片硅胶加热片的热源强度;δ—位置函数;(xi，yi，zi)—第i 片加热片的位置，其数学定义［6］如下:

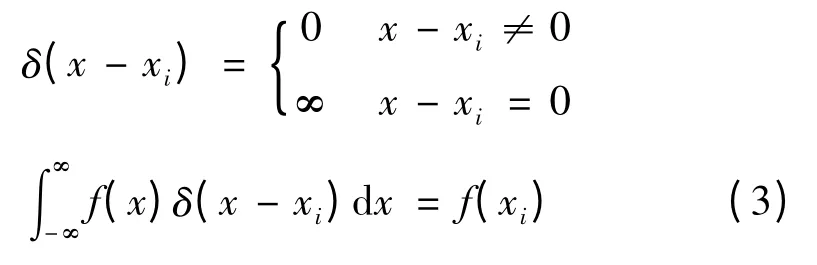
恒温反应器的整体结构不规则，其上各个零件在与周围环境不断进行换热的过程中，缸体内部的温度也在不断变化，这给初始条件的设定带来困难。笔者在实际工作环境中，测量恒温反应器的初始温度，得到其内部表面温度是在20．022 ℃～20．306 ℃，故本研究设定反应缸内部各点的初始温度条件为20 ℃。

再给定边界上的热流密度值即第二类边界条件，则有:

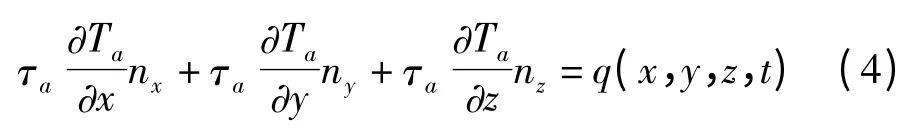
式中:τa—反应缸的热导率;Ta—恒温反应器内部的任意一点的瞬态温度场;nx，ny，nz—边界外法线上的方向余弦;q—加热片位置及加热时间的函数。

恒温反应器上箱盖，保温层等部件都与周围空气进行对流换热，为第三类边界条件，即:

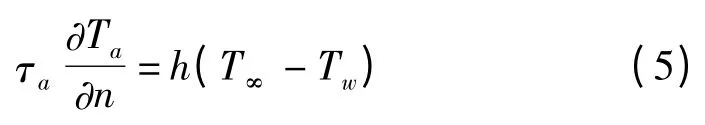
式中:n—反应缸内表面的外法线方向;h—表面传热系数;T∞—环境温度;Tw—反应缸内表面温度。

自然对流h 的值在1 W/(m2·K)～10 W/(m2·K)的范围内，随着加热过程的进行，恒温反应器缸体的上表面，保温层外表面与周围环境的换热系数也是处于不断地变化过程中。环境温度T∞取20 ℃。

反应缸、箱盖、液路联接器的温度都不是很高，故这里就不考虑其辐射边界条件。

反应缸内部的传热以及加热片与反应缸之间的传热都是以热传导的方式进行。

1．4 试验校准有限元模型

为了使建立的有限元模型在数值模拟过程中能真实地反映实际的物理模型的加热效果，笔者需要对建立的有限元模型进行试验校准。

恒温反应器分别在20 ℃和10 ℃的两种恒定环境温度下进行试验校准。试验校准的目标参数主要是有限元模型中的保温层与周围空气的换热系数、箱盖与周围空气的换热系数，有限元模型中4 块加热片的功率分布与实际值保持一致。

试验中的各个硅胶加热片［7］的功率利用的是没有进行功率分布优化的功率值，其功率分布示意图如图4 所示。

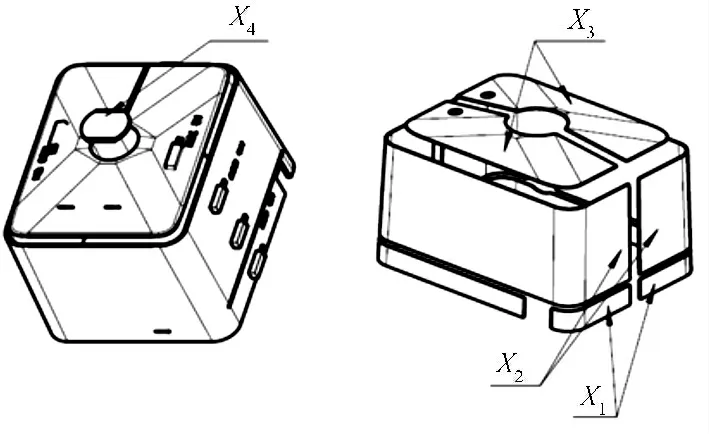
图4 加热片功率分布示意图

在110 V 的加热电压下，加热片功率分布为:X1=80 W，X2=310 W，X3=130 W，X4=5 W。

为了全面反映加热过程中反应缸内温度场的均匀性，笔者在反应缸内部加热的水中布置18 个防水温度传感器，温度传感器连接安捷伦型号为34972A 的数据采集仪［8］的功率利用的是没有进行功率分布优化的功率值，其功率分布示意图如图5 所示。

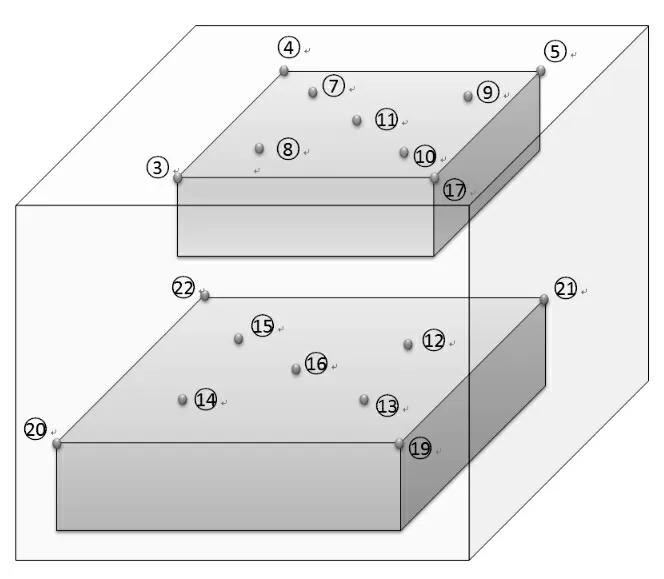
图5 温度传感器位置示意图

图6 测试试验平台

在恒定温度为20 ℃的环境中试验，试验测试时间为4 000 s，反应缸内部各点的升温曲线如图7 所示。

根据反应缸内部各测点的升温曲线，笔者通过改变有限元模型中的保温层与周围空气的换热系数、箱盖与周围空气的换热系数，得到了与试验模型吻合度很高的有限元模型［9］，该有限元模型就是校准后的有限元模型。本研究对该有限元模型进行的是瞬态温度场的求解，总时间设置为4 150 s，增量步为50 s，收敛公差为0．1%。在该20 ℃恒温环境中，最后得到的模拟升温曲线如图8 所示。

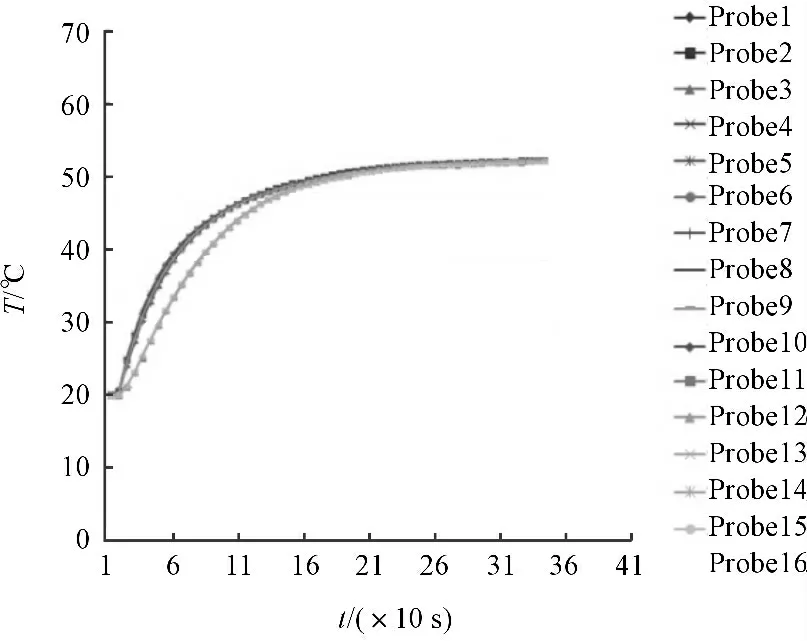
图7 反应缸内部各测点的升温曲线

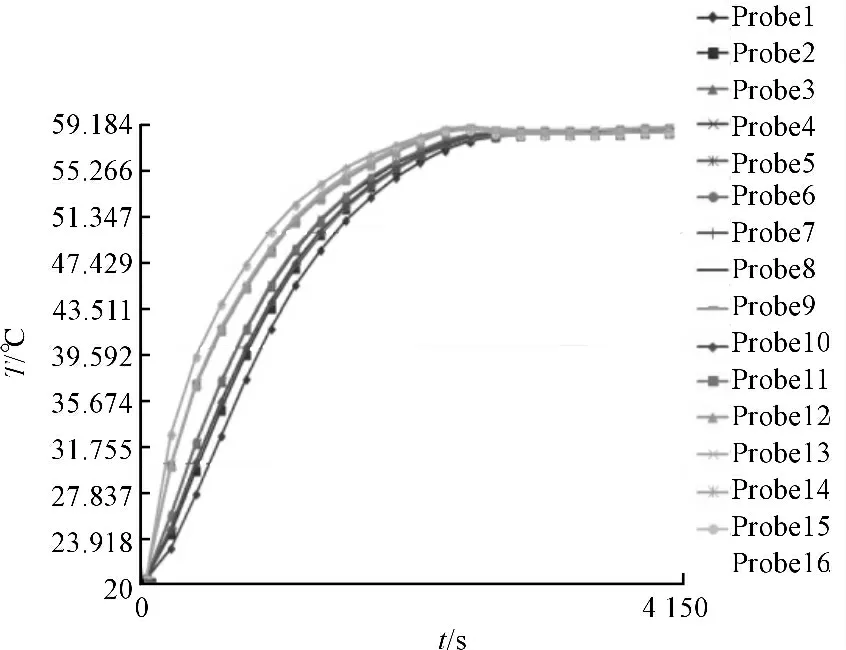
图8 数值模拟中的测点的升温曲线

同时由反应缸内部各测点的升温数据得:在20 ℃的恒温环境中，测温时间为4 000 s 时，反应缸内部温度场的温度差为0．337 ℃;在10 ℃的恒温环境中，测温时间为4 000 s 时，反应缸内部温度场的温度差为0．323 ℃，温度差都大于行业要求的0．2 ℃。因此，需要通过优化4 块加热片的功率分布以优化反应缸内部温度场均匀性。

2 优化方案与结果

2．1 利用均匀试验进行温度场的有限元模拟

均匀试验设计［10］适合安排多水平的试验，可大大减少试验的工作量，同时可以从尽可能少的试验次数中找到试验规律。

故本研究采用均匀试验法优化加热片的功率分布。已知目前在110 V 的加热电压下，加热片功率分布为:X1=80 W，X2=310 W，X3=130 W，X4=5 W。笔者取4 块加热片的功率X1、X2、X3、X4作为设计变量，作为试验的4 个因素，目标变量为4 000 s 时反应缸内部温度场的温差值Y。在之前试验的基础上并结合专业知识，确定每个因素的变化范围为:X1=60 W～100 W，X2=290 W～330 W，X3=110 W～150 W，X4=3 W～7 W。

每个因素取5 个水平，因素水平表如表2 所示。

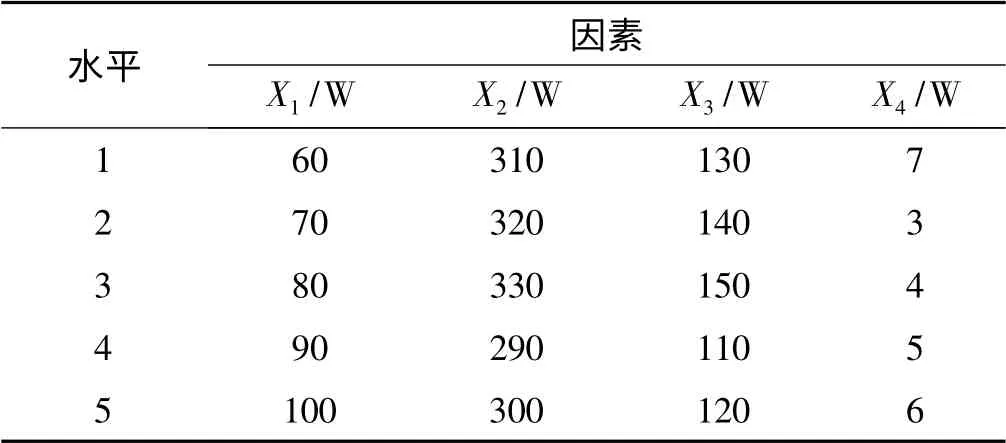
表2 因素水平表

该试验是4 因素5 水平试验，为提高试验精度和可靠性，选取均匀设计表U10(1010)，并使用拟水平法来安排模拟试验，由此得到的试验方案结合之前校准后的有限元模型进行模拟试验，模拟试验方案与结果如表3 所示。

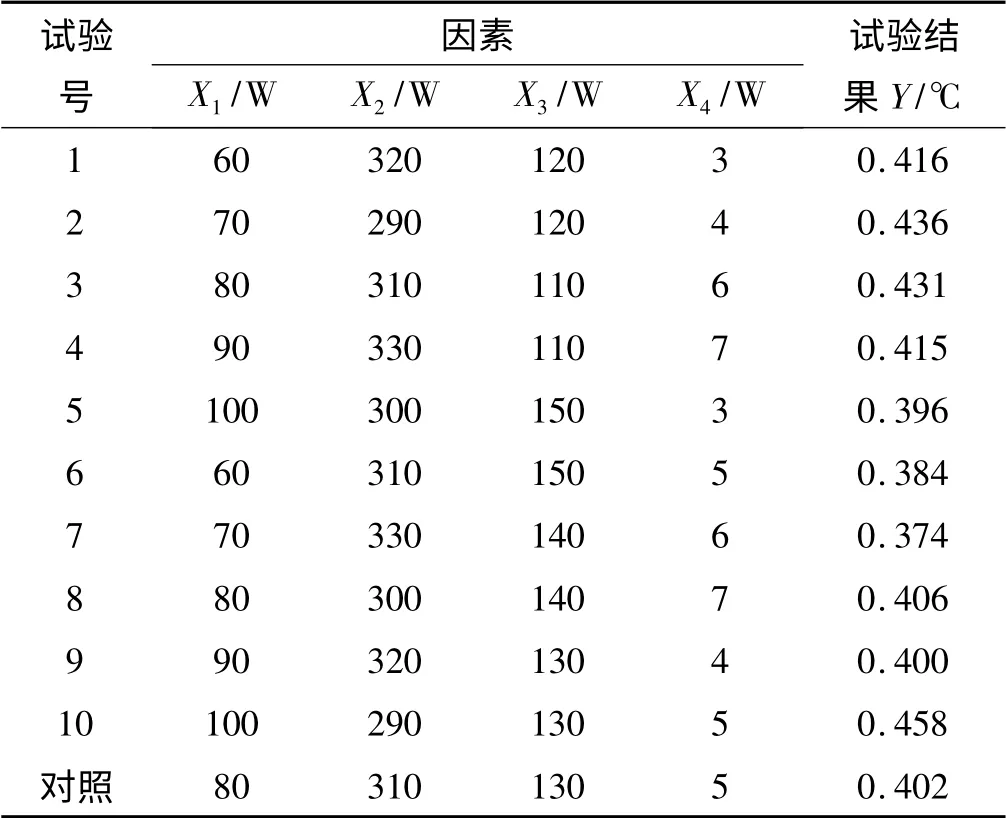
表3 模拟试验方案与结果

2．2 有限元模拟的结果分析

上述模拟试验方案的结果利用Matlab 经过多次多项式回归拟合，得如下的回归方程:

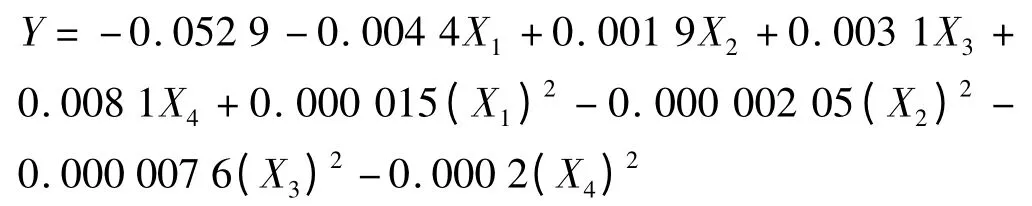
剩余标准差为0．002 9，所以回归模型的显著型很好。使用遗传算法进行回归方程的参数优化［11］，遗传算法的参数设置如表4 所示。

保持床铺整齐、清洁、干燥，盖被须轻暖，衣着避免过多，以免产生烦躁不安及过量出汗，内衣不应过紧，以免影响呼吸动作，及时更换尿布。高热出汗后及时更换衣服，避免受凉后加重病情。

表4 遗传算法参数设置

遗传算法的进化曲线如图9 所示。

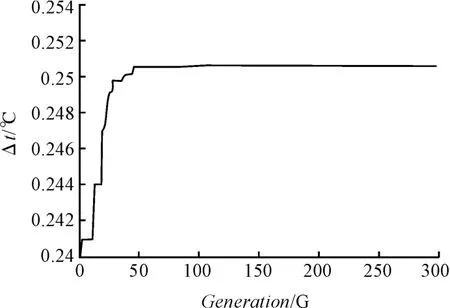
图9 进化曲线图

由图9 知，在进化到第100 代时得到最优解，优化的结果为:当X1=75 W、X2=330 W、X3=150 W、X4=3 W时，温度差Y 的值最小，为0．254 ℃。

2．3 优化结果的模拟验证

按照优化后的加热片功率分布:X1=75 W、X2=330 W、X3=150 W、X4=3 W，本研究在校准后的有限元模型上进行模拟试验，得到反应缸内部各测点的升温曲线如图10 所示。

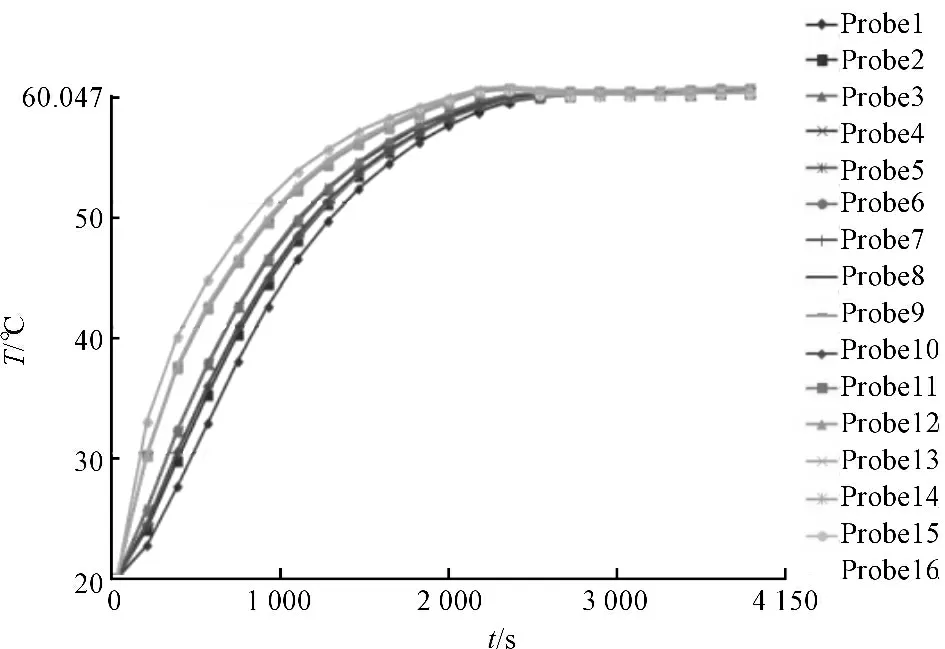
图10 模拟试验各测点温度升温曲线

同时本研究得到4 000 s 时温度场各测点的温度差为0．243 ℃，由之前试验得到实验值与模拟值的误差为25%得到优化后的实测温度差应小于0．2 ℃。

2．4 优化结果的现场试验验证

为了验证优化后的功率分布对反应缸加热温度场均匀性的影响，笔者对加热过程进行现场试验。本研究在20 ℃的恒温环境中进行试验，采用上述优化功率分布后加热片进行加热，加热时间为4 000 s，加热方式采用PID 控制器进行控制加热，同样采用安捷伦型号为34972A 的数据采集仪采集各测点的温度，传感器的布置如图7 所示。本研究得到4 000 s 时反应缸内部各测点的温度值，与之前的模拟试验的计算值进行对比，结果如表5 所示。

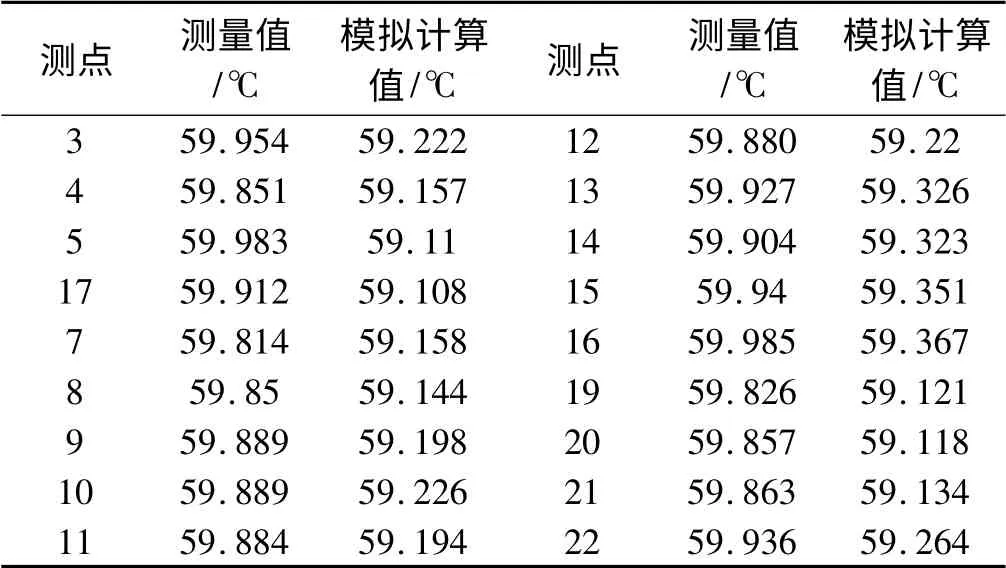
表5 温度场各测点测量值与模拟计算值比较

从表5 可知，在20 ℃的工况下，温度场温差的测量值与模拟计算值的吻合度很好，相对误差约为1%，同时温度场温差的测量值为0．171 ℃，小于0．2 ℃，满足了行业要求，说明对加热片功率分布的优化是成功的。

3 结束语

本研究应组织脱水机的恒温反应器加热系统温度场存在的均匀性问题对恒温反应器上加热片的功率分布进行研究，得出以下结论:

(1)根据恒温反应器加热系统的传热机理，建立了温度场的传热模型、有限元模型，通过试验成功校准了该有限元模型，对如何建立准确的有限元模型提供了参考。

(2)利用校准后的有限元模型进行了均匀模拟试验，结合遗传算法成功地优化了加热片的功率分布，有效地提高了温度场的均匀性，可以在工程实际中得到应用。

(3)模拟试验结果与温度场实际测量结果基本吻合进一步验证了建立的恒温反应器的有限元模型的合理性。

［1］潘路平．全自动组织脱水机的研制［D］． 天津:天津大学精密仪器系，2009．

［2］MATSUNAGA N． A New Method of Temperature Control for the Uniform Heating［C］//The 29th Annual Conference of the IEEE，Roanoke，2003:2097-2102．

［3］NANNO I，HASHIDA S，MATSUNAGA N，KAWAJI S．Experimental Study on Uniform Heating Control based on Temperature Difference Model［C］//Mechatronics，ICM 2007 4th IEEE International Conference． Kumamoto:［s．m．］，2007:1-6．

［4］NANNO I，HASHIDA S，MATSUNAGA N，KAWAJI S．Experimental Study on Uniform Temperature Control for Two-Dimensional Heating Plate Control［C］//Control，Automation and Systems，ICCAS International Conference． Seoul:［s．m．］，2007:1450-1455．

［5］何文斌，曾 攀，张 磊，等．基于有限元的400 MN 大型模锻压力机温度场分析［J］． 机械工程学报，2015，51(2):30-36．

［6］李金国，蒋 宁，高增梁，等．反应成型模具耦合温度场数值模拟与试验研究［J］．机械工程学报，2014，50(8):73-80．

［7］赵秀红，刘宝林．一种新型多温区恒温箱均温性的数值模拟与实验验证［J］．制冷学报，2015，36(2):27-33．

［8］包胜华，沈金美，王淑芬．Agilent 34972A 在温度传感器检测系统中的应用［J］．机电工程，2011，28(6):683-686．

［9］HETTEGGER M，STREIBL B，BIRO O，NEUDORFER H．Identifying heat transfer coefficients on the end-winding of an electrical machine by measurements and simulations［J］．Proc． ICEM，2010，39(1):1-5．

［10］闫 伟，张 浩，陆剑锋，等．直喷式柴油机燃烧系统的均匀试验设计研究［J］． 机械工程学报，2005，41(1):212-215．

［11］刘文胜，鲍玉彬，孙 雷，等．基于遗传算法回归分析技术研究［J］．计算机工程与应用，2004(21):94-97．