基于改进支持向量机的湖北电网特高压规划研究
王 枫 ,上官安琪 ,夏俊丽
(1.国网湖北省电力公司,湖北武汉430077;2.武汉大学电气工程学院,湖北武汉430072)
0 引 言
“十三·五”是全面建设小康社会的关键时期,随着湖北省社会经济的飞速发展,全省电力需求快速增长。湖北省化石能源匮乏,水电基本开发完毕,火电用煤供应压力加大,经济发展需求与能源资源约束的矛盾日益突出,这将使湖北在很长一段时间内面临电力供应紧张,建设特高压输电从外省输入电力刻不容缓。因此,利用科学合理的方法对湖北省未来电力需求进行预测和分析,对经济发展政策的制定和特高压输送容量等的有效规划有着十分重要的意义。
中长期电力负荷预测是电力平衡分析的基础,其准确性直接影响电力平衡分析的有效性。由于中长期负荷受到许多非线性因素及不确定因素的影响,进行准确的中长期负荷预测非常困难。目前应用最多的中长期负荷预测方法大致分为参数估计方法和人工智能方法[1],参数估计方法主要包括回归分析法[2]和灰色系统方法[3];人工智能方法主要包括神经网络[4]、证据理论[5]、数据挖掘技术[6]和专家系统[7]等。其中参数估计方法的精确度不是很理想,而以神经网络为代表的人工智能方法需要的数据样本很大,这对于中长期负荷预测来说是很不现实的。
支持向量机(SVM)是20 世纪90年代中期基于统计学理论的VC 维(Vapnik-Chervonenkis dimension)理论和结构风险最小化原则而提出的一种新的机器学习方法,最初应用于小样本、非线性的模式识别分类问题,随后应用于非线性拟合并表现出良好的性能。由于支持向量机对训练样本的数量要求少,泛化能力强,理论上以及实际应用,都证明其性能比神经网络方法更优,因此更加适用于中长期负荷预测。本研究采用支持向量机对湖北省中长期电力负荷进行预测。由于支持向量机模型参数的选择对预测结果的精确度有很大影响,而这些参数一般都根据经验,人工试验选取,非常不利于支持向量机的推广使用,也不能达到最好的预测效果。
本研究将利用遗传算法来实现支持向量机参数的自动选取,通过实例验证该方法的有效性。得到中长期负荷预测的理想结果后,进一步对湖北电网进行电力平衡,对特高压直流的建设规划提出指导性意见。
1 湖北电网电源装机现状及建设规划
获取电源装机现状和未来建设规划是电力平衡分析中计算系统可利用容量的必需步骤,湖北电网的装机现状和建设规划如下。
1.1 湖北电网电源装机现状
截至2013年底,湖北省全口径发电装机容量达到6.17 ×107kW(含三峡电站2.24 ×107kW),其中水电装机3.732 ×107kW,占总容量的60.5%;火电装机2.412 × 107kW,占39. 1%;新能源装机2. 686 ×105kW,占0.4%。全省统调总装机容量5.368 75 ×107kW,占全口径发电装机的87%。
湖北电网电源结构详如表1 所示。
1.2 湖北电网建设规划
根据湖北省“十二五”、“十三五”水电电源规划,煤电项目的规划及建设进展情况,以及新能源电源的建设日程,截至2020年,湖北省全口径发电装机容量预计达到7.292 ×107kW。本研究选取的电力平衡水平年为2015、2016、2017、2020年,各水平年湖北电网全口径发电装机具体规划如表2 所示。

表1 湖北电网电源结构
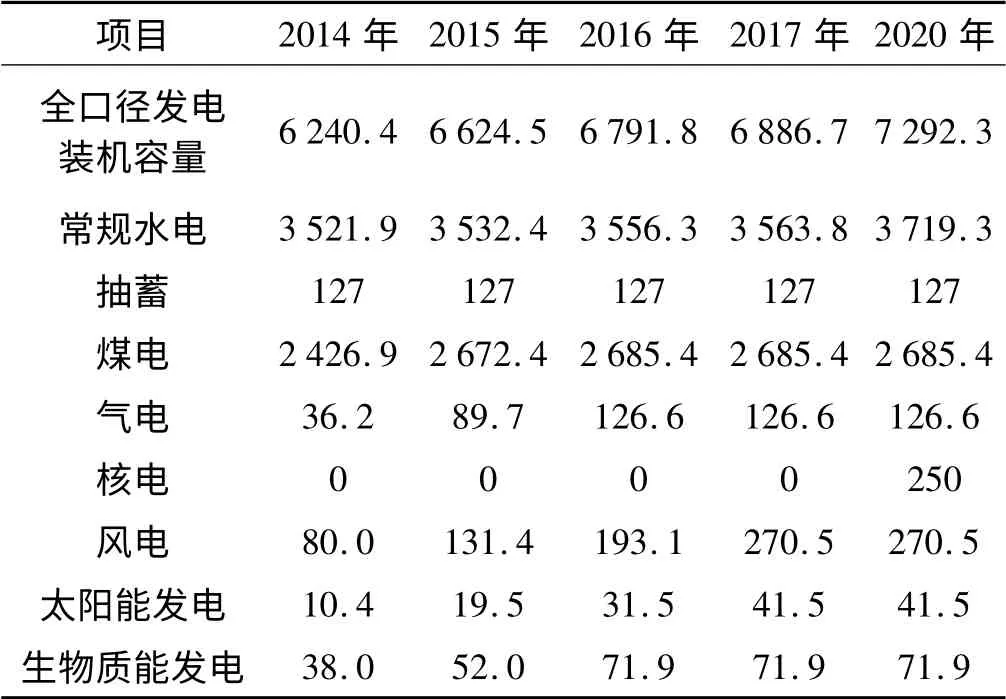
表2 2014~2020年湖北电网全口径发电装机规划 单位:万kW
2 基于改进支持向量机的中长期电力负荷预测方法
全社会最大负荷的预测是电力平衡分析中的重要一步,属于中长期负荷预测的范畴。根据引言的分析,本研究将采用支持向量机进行预测。用于预测的支持向量机称为支持向量回归机(support vector regress,SVR)主要有Vapnik 提出的ε-SVR[8]和Schölkopf 等提出的v-SVR[9]。本研究将采用ε-SVR 对湖北省中长期电力负荷进行预测,并利用遗传算法实现SVR 参数的自动选取,克服SVR 参数选取依赖多次人工试验的不足。
2.1 支持向量回归机算法原理
假设训练样本集为{(x1,y1),i =1,2,…,n,x1∈Rn,y1∈R}。SVR 的原理是通过非线性映射φ(x)将数据x 映射到高维特征空间F 中,并在F 中利用式(1)中的估计函数f(x)进行线性回归[10]:

式中:ω—权值向量,b—偏置。
其函数逼近问题等价于式(2)中的期望风险函数Rrge[f]最小:

式中:Rrge[f]— 期望风险;Remp[f]— 经验风险,Remp[f]=;λ—常数。
利用结构风险最小化思想构造损失函数,通过求解式(3)中带有约束条件的最优问题,即可确定回归函数f(x):

这个问题其实就是式(4)所示的对偶问题:

式中:ai,—对偶问题的参数。
求解式(4)可得到支持向量机回归函数:
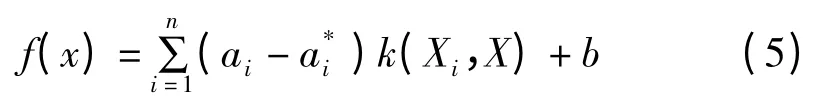
式中:k(Xi,X)—核函数,一般选取最常用的高斯核函数。SVR 预测的关键是获取ε,C 和σ 的最优取值组合。
笔者采用遗传算法来实现这些参数的自动选择,其优点是能自适应地调整搜索方向,不需要确定的规则,并且可以使所选取的参数具有一定的概率接受调整,避免陷入局部极小值而找到全局最优解,缩短参数寻优的时间,大大增加SVM 预测模型的通用性。
2.2 基于改进SVR 的中长期电力负荷预测步骤
基于改进SVR 的负荷预测具体算法步骤为:
(1)将原始的负荷数据进行归一化预处理;
(2)参数初始化。设定参数范围C∈(0,106],ε∈[0,1],σ∈(0,2];遗传算法最大进化代数maxgen=200,种群最大数量sizepop=100,代沟ggap=0.9;
(3)利用遗传算法确定SVR 的最优参数组合bestC,bestσ,bestε;
(4)利用处理好的负荷数据和优化后的参数训练出支持向量回归机预测模型model;
(5)将训练样本的输入矩阵作为测试矩阵输入model,得到测试结果,与训练样本的目标矩阵对比来验证所得预测模型的准确性;
(6)将待预测年份的样本输入model,得到结果。
3 湖北电网电力平衡
本研究利用第1 节中介绍的湖北电网装机现状和未来规划通过一定规则计算得出系统可利用容量,利用第2 节中介绍的基于改进SVR 的中长期电力负荷预测方法计算得出系统最大负荷,一并考虑网损、厂用电和备用容量这些因素来进行湖北电网电力平衡的分析。
3.1 电力平衡计算方法
电力平衡是电力需求与供应之间的平衡。本研究中电力平衡主要按下列公式进行:

式中:系统可利用容量—主要考虑湖北省装机可利用容量,以及国网规划送入湖北的电力;系统需要容量—系统最大负荷、网损、厂用电及备用容量之和[11]。
详细的系统可利用容量和系统需要容量的计算结果,详见3.3 节。
为了分析远景湖北电网区域电力交换规模,本研究分别在丰大方式和枯大方式下对湖北电网进行电力平衡[12],计算水平年为2015、2016、2017、2020年。
3.2 2015—2020年(“十三·五”)全社会最大负荷预测
笔者利用本研究提出的遗传算法优化的支持向量机对湖北电网2015年~2020年的全社会最大负荷进行预测,采用1995年~2013年的全社会最大负荷值来训练预测模型,训练时将前5 个历史值作为输入变量,第6年的值作为目标变量,通过遗传算法优化后,得到参数最优的SVR 模型。预测时同样用前5年的数据来预测第6年。
为了验证所得SVR 模型的效果,笔者将1995年~2012年的数据作为测试变量输入模型,得到2000年~2013年的预测值,并与2000~2013年的实际值比较。作为对比,笔者采用BP 神经网络对同样的数据以相同的方式进行预测,采用平均相对误差eMAPE作为比较的依据:

式中:A(i)—第i年的真实值,F(i)—第i年的预测值,n—预测总年数。
通过libsvm3.18 工具包和Matlab 的接口编程所得SVR 和BP 神经网络的预测结果如表3、图1 所示。遗传算法优化得到的最优参数组合如表4所示。

表3 SVR 和BP 神经网路预测结果比较

表4 遗传算法优化后的最优参数组合

图1 SVR 和BP 神经网络拟合结果与实际值的比较
表4 中,SVR 和BP 神经网络预测结果的平均相对误差eMAPE分别是1.33%和4.99%。可以看出,遗传算法优化后的SVR 模型的精度明显高于BP 神经网络模型,因此使用改进SVR 模型预测湖北电网2014年~2020年的全社会最大负荷可以达到更好的效果。电力平衡分析所选取的几个水平年的预测结果如表5所示。
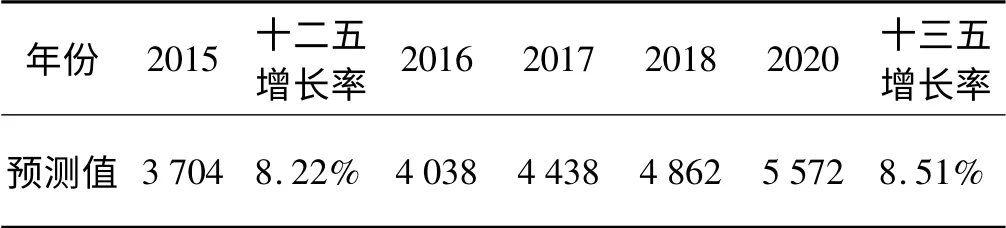
表5 各水平年湖北电网全社会最大负荷预测值 单位:万kW
3.3 2015~2020年(“十三·五”)湖北电网电力平衡
结合3.1 和3.2 对系统可利用容量和系统需要容量的计算,湖北电网“十三·五”电力平衡如表6 所示。

表6 水平年湖北电网电力平衡表 单位:万kW
由表6 可知,2015年湖北电网在枯大方式下将出现电力缺口2.3 ×105kW,主要原因是枯水季节水电发电能力大幅下降,火电则因电煤供应不足出现缺煤停机。之后几年缺电更为严重,2017年枯大方式下电力缺口将达到6.18×106kW,丰大方式下仍缺电3.34×106kW,已由季节性缺电向全年性缺电转变,主要原因是湖北省电源装机不足以及受电不足。到2020年,枯大方式下电力缺口将达到1.533 ×107kW,丰大方式下仍缺电1.332 ×107kW,电力缺口相当严重。
4 结束语
本研究提出了一种基于遗传算法改进的支持向量机的中长期电力负荷预测方法,预测了湖北电网“十三·五”期间的全社会最大负荷,并与常用的BP 神经网络法的预测结果进行对比,研究结果表明,该方法的预测精度比BP 神经网络提高了3.66%。其次结合湖北电网电源装机规划与负荷预测结果进行了电力平衡,分析湖北电网“十三·五”期间的电力供需形势。研究结果表明,湖北电网将从2015年枯大方式运行时出现电力缺口,2017年由季节性缺电向全年性缺电转变,到2020年电力缺口将达到相当严重的1.533 ×107kW。因此,为保障电力供需平衡,湖北电网必须在“十三·五”期间加快特高压建设进程,快速推进省外受电通道的建设投运。
[1]康重庆,夏 清,张伯明.电力系统负荷预测研究综述与发展方向的探讨[J]. 电力系统自动化,2004,18(17):1-11.
[2]毛李帆,江岳春,姚建刚,等.采用正交信号修正法与偏最小二乘回归的中长期负荷预测[J].中国电机工程学报,2009,29(16):82-88.
[3]张伏生,刘 芳,赵文彬,等.灰色Verhulst 模型在中长期负荷预测中的应用[J]. 电网技术,2003,27(5):37-39,81.
[4]李春祥,牛东晓,孟丽敏,等,基于层次分析法和径向基函数神经网络的中长期负荷预测综合模型[J].电网技术,2009,33(2):99-104.
[5]倪 明,高晓萍,单渊达.证据理论在中期负荷预测中的应用[J].中国电机工程学报,1997,17(3):56-60.
[6]牛东晓,谷志红,邢 棉,等. 基于数据挖掘的SVM 短期负荷预测方法研究[J]. 中国电机工程学报,2006,26(18):6-12.
[7]付 宾,罗伟林. 基于LSSVM-PID 的船舶航向控制[J].机电工程,2013,30(5):632-635.
[8]VAPNIK. Statistical learning theory[M].New York:Wiley,1998.
[9]SCHÖLKOPF B,SMOLA A,WILLIAMSON R C,et al.New support vector algorithms[J]. Neural Computation,2000,12(5):1207-1245.
[10]王守成,支持向量机建模预测与控制[M].北京:气象出版社,2009.
[11]敖蕾蕾,王慧芳,杜振东.电网状态检修决策研究[J].机电工程.2014,31(5):639-643.
[12]罗 龙,陈为化.浙江省特高压电网规划研究[J].机电工程,2009,26(10):70-73.

