利用修正的Hargreaves公式计算青海湖流域参考作物潜在腾发量

李岳坦，李小雁崔步礼

（1.北京师范大学 资源学院，北京 100875；2.中国科学院大学 资源与环境学院，北京 100045）

利用修正的Hargreaves公式计算青海湖流域参考作物潜在腾发量

李岳坦1，2，李小雁1，崔步礼1

（1.北京师范大学 资源学院，北京 100875；2.中国科学院大学 资源与环境学院，北京 100045）

根据青海湖流域刚察气象站1958—2006年的逐日气象资料，分别采用Penman-Monteith公式和Hargreaves公式对参考作物潜在腾发量进行了计算并对两种方法的计算结果进行了对比分析，发现两种方法的计算结果存在较大差异。为了提高Hargreaves公式在该地区的适用性，引入平均相对湿度因子对Hargreaves公式进行了修正，并利用刚察气象站2007—2012年的逐日气象资料对Hargreaves公式修正式的计算结果进行了验证，发现对Hargreaves公式的修正结果非常好，在青海湖流域可以作为计算参考作物潜在腾发量的一种计算方法而使用。

青海湖流域；Penman-Monteith公式；Hargreaves公式；参考作物潜在腾发量

参考作物潜在腾发量（ ET0）是计算植物耗水量的一个重要参数，也是水资源管理、灌溉工程设计以及规划和环境评价的一个重要依据。1994年，联合国粮农组织（FAO）给参考作物潜在腾发量规定了明确的定义，即参考作物潜在腾发量为一假想的参考作物冠层的蒸发蒸腾速率，即假设作物高度为0.12 m，固定的叶片阻力为70 s·m-1，反射率为0.23，非常类似于表面开阔，高度一致，生长旺盛，完全覆盖地面而不缺水的绿色草地的蒸发蒸腾量（Allen et al，1994）。目前计算参考作物潜在腾发量的经验公式多达数十种，相对而言，利用Penman-Monteith公式计算的参考作物潜在腾发量无论在干旱地区还是在湿润地区都与实测值非常接近（Allen et al，1998），使用Penman-Monteith公式所必需的气象资料包括最高气温、最低气温、平均气温、相对湿度、风速、日照时数等，然而在世界范围内许多地区的气象站都难以全部提供这些完整的数据资料（Xu and Singh，2002），这在很大程度上限制了Penman-Monteith公式的使用。因此，使用较少气象资料的计算方法在许多地方得到了广泛应用。

Hargreaves等人于1985年建立了Hargreaves公式，该公式只需日最高气温、日最低气温、日平均气温和外太空辐射就可以计算参考作物潜在腾发量。日最高气温、平均最低气温和日平均气温在绝大多数气象站点都有观测，外太空辐射资料可以根据当地纬度查阅FAO相关文献得到（Hargreaves and Samni，1985）。因为Hargreaves公式所需数据资料容易获得，故而该公式自从提出以来，国外学者对该公式进行了大量的研究，并针对不同的气候条件提出了一些改进建议（Xu and Singh，2002；Allen et al，1998；Jensen et al，1990；Martínez-Cob and Tejero-Juste，2004；Gavilán et al，2006；Droogers and Allen，2002；Saeed，1986；Amatya et al，1995）。

近年来，国内部分学者开始对Hargreaves公式在国内部分地区的适用性进行了研究和分析，王声峰等（2008）通过利用Hargreaves公式对河南省新乡市4个典型水文年参考作物蒸散量的计算，验证了Hargreaves公式在半干旱区的适用性；杨永红等（2009）利用改进的Hargreaves公式计算了拉萨地区的参考作物蒸发蒸腾量；范丽萍等（2007）通过对Hargreaves公式的计算结果与Priestley-Taylor的计算结果进行比较，验证了Hargreaves公式在西安地区的适用性；王新华等（2006）利用Hargreaves公式计算了甘肃张掖的参照作物需水量，并通过与Penman-Monteith公式的计算结果进行比较从而验证了Hargreaves公式在西北干旱区的适用性；赵永等（2004）利用Hargreaves公式对陕西杨凌地区的参考作物蒸发蒸腾量进行了计算。但总体来说，国内对Hargreaves公式的应用和研究相对较少，Hargreaves公式在国内有待于进行进一步的推广和应用。

青海湖流域地处高寒半干旱区，具有独特的高原、水文、气候等环境条件，流域自然条件复杂，它是国际重要湿地和和优先保护湿地生态系统。青海湖对于调节青海乃至我国西部和西北地区的气候，起着非常重要的作用，青海湖流域作为青藏高原的重要组成部分，是西部干旱区、东部季风区、青藏高原区三大区域的交汇地带，对全球气候变化的响应较为迅速。近年来，由于气候变化和人类活动的影响，青海湖流域出现了湖泊水位下降、植被退化等一系列生态环境问题。青海湖流域的生态环境变化已经引起了世界范围内的关注，对青海湖流域水资源管理、生态需水量以及水资源优化配置的研究已经成为亟需解决的问题。参考作物潜在腾发量的是对这些问题进行研究过程中的一个重要的指标和参数，但是青海湖流域气象站点较少，仅有刚察站一个国家气象站点，地方站点仅有天峻，除此之外还有布哈河口、上涣仓、沙陀寺、黑马河和一郎剑等几个水文站进行着气象资料观测。总体来说，仅有刚察站的观测资料较全，从而导致利用Penman-Monteith公式计算该地区的潜在腾发量适用性不强。本文通过对Penman-Monteith公式和Hargreaves公式需要输入的气象因子进行比较，采用主成分分析后引入湿度因子，对Hargreaves公式进行了修正并对该修正式进行了评价，以期为青海湖流域参考作物潜在腾发量的计算提供一种准确并且能够广泛适用的方法。

1 材料与方法

1.1 参考作物潜在腾发量的计算

1）Penman-Monteith公式

计算参考作物潜在腾发量的Penman-Monteith公式为（Abdelhadi et al，2000；Sumner and Jacobs，2005；Gong et al，2006）：

式中前者为辐射项，后者为空气动力学项：

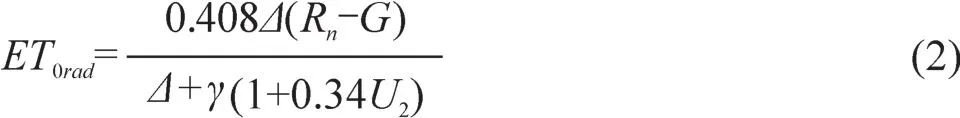
式中，ET0为参考作物潜在腾发量（mm·d-1）；Δ为饱和水气压与温度曲线的斜率（kPa·℃-1）；R为参考作物冠层表面净辐射（MJ/（m2·d-1））；γ为干湿表常数（kPa·℃-1）；U2为2 m高度处的风速（m·s-1）；es为饱和水气压（kPa）；ea为实际水气压（kPa）。

2）Hargreaves公式

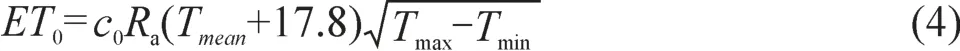
式中，Ra为大气边缘太阳辐射，可根据时间与地理位置数据计算；c0为转换系数，当Ra以mm·d-1为单位时，c0=2.3×10-3；当Ra以MJ/（ m2·d）为单位时，c0=9.39×10-4；Tmean为日平均气温（℃）；Tmax为日最高气温（℃）；Tmin为日最低气温（℃）。

1.2 统计分析

本文使用误差分析对Hargreaves公式的修正式进行评价，主要统计量有绝对偏差（BE）和相对偏差（R），计算公式为：

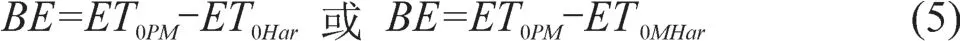
1.3 对两个公式需要输入的气象因子进行比较

Penman-Monteith公式计算过程复杂，需要的气象因子较多，主要有最高气温、最低气温、平均气温、平均风速、日照时数和平均相对湿度等。而Hargreaves公式仅需要最高气温、最低气温、平均气温和外太空辐射就可以计算参考作物潜在腾发量，最高气温、最低气温和平均气温在绝大多数气象站点都有观测，外太空辐射资料可以根据当地纬度查阅FAO相关文献得到。

2 Hargreaves公式的修正依据

主成分分析是1901年Pearson对非随机变量引入的，1933年Hotelling将此方法推广到随机向量的情形，其主要目的是希望用较少的变量去解释原来资料中的大部分变异，将许多相关性很高的变量转化成彼此相互独立或不相关的变量（即主成分），其中每个主成分都是原始变量的线性组合，且各个主成分之间互不相关，这就使得主成分比原始变量具有某些更优越的性能（杨虎等，2004）。

本文利用青海湖流域刚察气象站的1958—2006年的逐日气象资料，采用IBM Spss Statistics 19.0进行主成分分析和统计，原始数据指标标准化处理亦通过该软件系统进行，以消除指标量纲及数量级的影响。

2.1 分析结果

1）相关系数矩阵

相关系数矩阵表（表1）中右上角部分是日最高气温、日最低气温、日平均气温、日照时数、平均风速和平均相对湿度等指标间的相关系数，左下角部分是相应的相关系数的单侧显著性水平。由表1可知，日最高气温、日最低气温、日平均气温和平均相对湿度4者之间的相关系数较高，达到了极显著水平。

2）总方差解释

根据特征值大于1的原则，累积方差贡献率可达72.384％，具体可见总方差解释（表2）。由表2可知，前2个主成分包含了日最高气温、日最低气温、日平均气温、日照时数、平均风速和平均相对湿度等原指标的绝大部分信息，可以代替原来6个原始变量的影响关系。

表1 相关系数矩阵Table 1 Correlation matrix

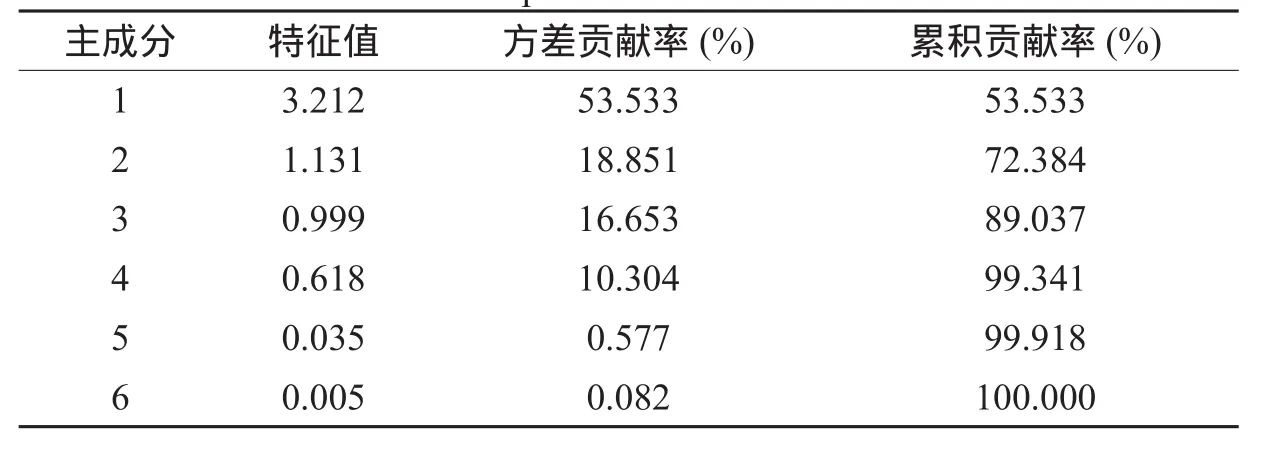
表2 总方差解释Table 2 Explaination of total variance

3）初始因子载荷矩阵

表3为初始因子载荷矩阵，该表反映了2个主成分与原始变量之间的相关程度，表中标示“*”的数据表示相应主成分与原始变量的相关程度较高，影响关系十分重要。

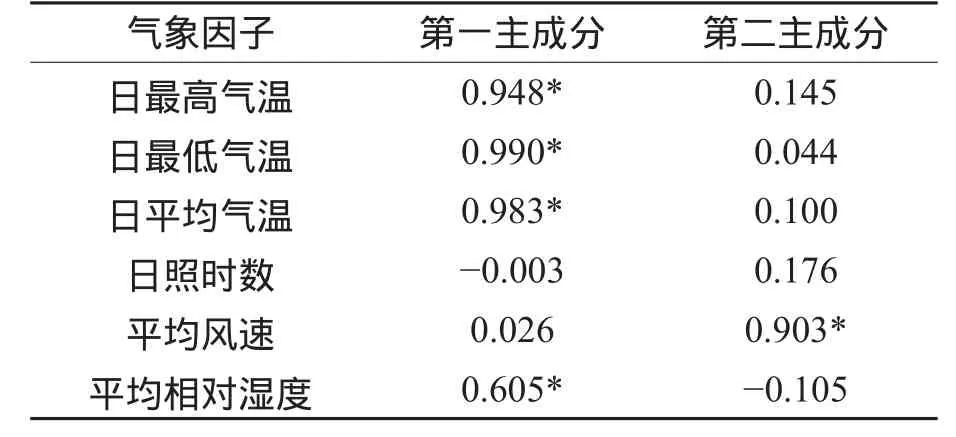
表3 初始因子载荷矩阵Table 3 Component Matrix

2.2 修正依据

从初始因子载荷矩阵可以看出：第一主成分与日最高气温、日最低气温、日平均气温和平均相对湿度4个气象因子之间具有显著相关性；第二主成分与平均风速具有显著相关性。此外，通过表2可以知道：第一主成分的方差贡献率达到了53.533％，包含了一半以上的信息，既然日最高气温、日最低气温、日平均气温和平均相对湿度4个气象因子具有显著相关性且包含了大多数信息，说明它们是第一主成分中较为重要的气象因子，且平均相对湿度尤为重要。故而，考虑到平均相对湿度对参考作物潜在腾发量具有重要影响，在Hargreaves公式引入平均相对湿度气象因子，从而建立Hargreaves公式的修正式。

3 Hargreaves公式修正式

3.1 数据资料与方法

根据青海湖流域刚察气象站1958—2006年逐日气象资料，分别利用Penman-Monteith公式和Hargreaves公式计算刚察站的逐日参考作物潜在腾发量多年平均值并对结果进行回归分析，为方便比较，定义Penman-Monteith公式计算的参考作物潜在腾发量为ET0PM，Hargreaves公式计算的参考作物潜在腾发量为ET0Har，以ET0PM为分析比较的标准值。

3.2 Hargreaves公式修正式的建立

通过主成分分析，已知平均相对湿度是一个重要的气象因子。因此，在Hargreaves公式中引入平均相对湿度因子，建立Hargreaves公式的修正式为：

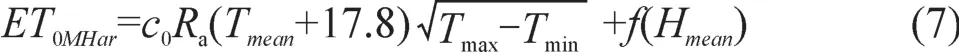
式中，ET0MHar为Hargreaves公式中引入平均相对湿度因子后计算的参考作物潜在腾发量；f（Hmean）为平均相对湿度的函数；其它符号意义同前。

3.2 平均相对湿度函数的推求

以刚察站的（ET0PM-ET0Har）为因变量，以Hmean为自变量，将ET0PM、ET0Har和Hmean的多年平均值代入各计算公式，利用Microsoft Excel 2013进行回归分析（图1），得到非线性回归趋势方程为：

图1 Hargreaves修正式回归系数的推求Fig.1 Regression coeff cient calculation of modif ed Hargreaves equation

由图1可知，判定系数R2=0.9122，相关性很好。因此，通过回归建立的青海湖流域Hargreaves公式的修正式为：

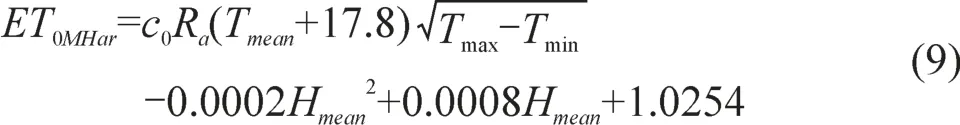
4 对Hargreaves公式修正式的评价

4.1 逐日参考作物潜在腾发量值对比分析

利用青海湖流域刚察气象站2007—2012年逐日气象资料，采用Penman-Monteith公式和Hargreaves公式的修正式计算多年平均日参考作物潜在腾发量并进行对比分析。利用Penman-Monteith公式、Hargreaves公式和Hargreaves公式的修正式计算的参考作物潜在腾发量的逐日分布曲线见图2。

图2（a）为利用Penman-Monteith公式和Hargreaves公式计算的逐日参考作物潜在腾发量，从图中可以看出，两个公式的计算结果在7、8、9三月较为接近，在其它月份Penman-Monteith公式的计算值明显大于Hargreaves公式的计算值，尤其在冬季，两个公式计算结果的差异明显，这主要是在7、8、9三月青海湖流域的降水较多，而在冬季的降水较少造成相对湿度的变化引起的。通过对Hargreaves公式引入平均相对湿度作为输入影响因子后，修正了由于湿度变化而造成的偏差，见图2（b），由图2（b）可以看出，Hargreaves公式的修正式计算结果与Penman-Monteith公式的计算结果十分吻合。

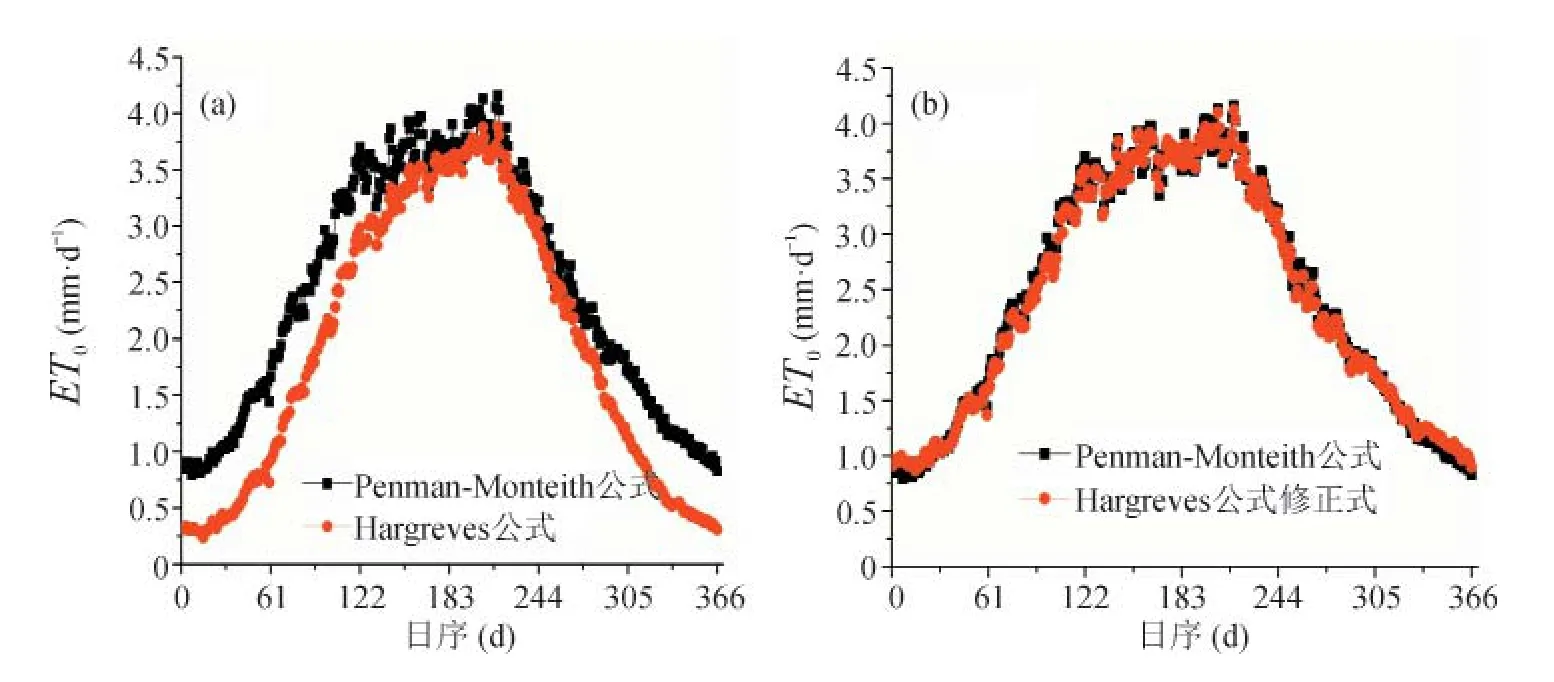
图2 Hargreaves公式修正前后与Penman-Monteith公式逐日ET0比较Fig.2 Daily ET0comparison of Penman-Monteith equation，Hargreaves equation and modif ed Hargreaves equation

4.2 逐日参考作物潜在腾发量偏差对比

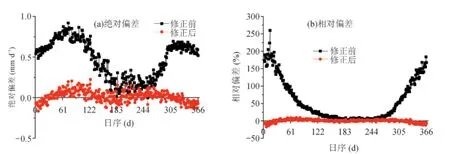
图3 Hargreaves公式修正前后与Penman-Monteith公式逐日ET0偏差比较Fig.3 Daily ET0deviations comparison of Penman-Monteith equation，Hargreaves equation and modif ed Hargreaves equation

青海湖流域刚察气象站修正的Hargreaves公式与Penman-Monteith公式计算的逐日参考作物潜在腾发量介于-0.17～0.22 mm·d-1（图3（a）），相对偏差介于-17.38～9.50％（图3（b）），超过15％的仅有1 d，超过10％的仅有12 d占全年3.3％；修正结果显示在2—11月份相对偏差全部介于±10％之间，绝大部分误差极小，修正效果较好。

4.3 逐日参考作物潜在腾发量相关性比较

图4为利用修正的Hargreaves公式与Penman-Monteith公式计算的逐日参考作物潜在腾发量的相关性比较，两种计算方法计算的逐日参考作物潜在腾发量的逐日回归方程为ET0PM=1.008ET0MHar，曲线斜率接近于1，说明两种方法的计算结果较为接近，此外判定系数R2=0.9959（P＜0.01，双尾），达到了极显著水平。利用修正的Hargreaves公式计算的参考作物潜在腾发量年值为873 mm，而利用Penman-Monteith公式计算的参考作物潜在腾发量年值为878 mm，二者也较为接近。从总体上来说，对Hargreaves公式的修正结果非常好，在青海湖流域可以作为计算参考作物潜在腾发量的一种计算方法而使用。

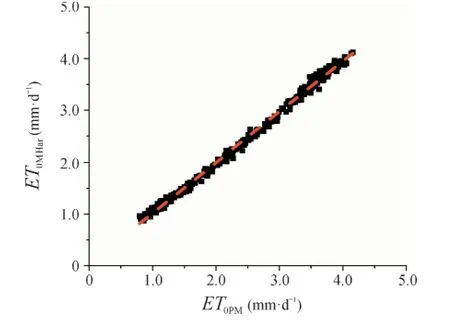
图4 利用修正的Hargreaves公式与Penman-Monteith公式计算的逐日参考作物潜在腾发量的相关性比较Fig.4 Revelant comparison of daily ET0between modif de Hargreaves eauation and Penman-Monteith equation

5 结论

1）经过主成分分析，青海湖流域刚察气象站的平均相对湿度对参考作物潜在腾发量有重要的影响。因此在Hargreaves公式中引入平均相对湿度因子对Hargreaves公式进行了修正。

2）以Penman-Monteith公式的计算结果为参照标准，修正的Hargreaves公式与Penman-Monteith公式计算的逐日参考作物潜在腾发量介于-0.17～0.22 mm·d-1，相对偏差介于-17.38～9.50％，超过15％的仅有1 d，超过10％的仅有12 d占全年3.3％；利用修正的Hargreaves公式计算的参考作物潜在腾发量年值为873 mm，而利用Penman-Monteith公式计算的参考作物潜在腾发量年值为878 mm，二者也较为接近。

3）本文通过对Hargreaves公式进行修正，可以为地处高寒半干旱地区并且气象资料缺乏的区域提供一种可供选择的参考作物潜在腾发量的计算方法。

范丽萍，贾忠华，罗 纨. 2007.西安地区Priestley-Taylor和Hargreaves方法应用比较[J].水资源与水土工程学报，18（2）：54-61. [Fan L P，Jia Z H，Luo W. 2007. Comparison with the application of Priestley-Taylor and Hargreaves methods in Xi'an [J]. Journal of Water Resources and Water Engineering，8（2）：54-61.]

王声峰，段爱旺，张展羽. 2008. 半干旱地区不同水文年Hargreaves和P-M公式对比分析[J].农业工程学报，24（7）：29-33. [Wang S F，Duan A W，Zhang Z Y. 2008. Comparison and analysis of Hargreaves equation and Penman-Monteith equation during the different hydrological years in the semi-arid region [J]. Transactions of the Chinese society of agricultural engineering，24（7）：29-33.]

王新华，郭美华，徐中民. 2006.分别利用Hargreaves和PM计算西北干旱区ET0的比较[J].农业工程学报，22（10）：21-25. [Wang X H，Guo M H，Xu Z M. 2006. Comparison of estimating ET0in arid-area of Northwest China by Hargreaves equation and Penman-Monteith equation [J]. Transactions of the Chinese society of agricultural engineering，22（10）：21-25.]

杨 虎，刘琼荪，钟 波. 2004. 数理统计[M].北京：高等教育出版社. [Yang H，Liu Q S，Zhong B. 2004. Mathematical statistics [M]. Beijing：Higher education press，199-207]

杨永红，张展羽. 2009.改进Hargreaves方法计算拉萨参考作物蒸发蒸腾量[J].水科学进展，20（5）：614-618. [Yang Y H，Zhang Z Y. 2009. Method for calculating Lhasa reference crop evapotranspiration by modifying Hargreaves [J]. Advances in water science，20（5）：614-618.]

赵 永，蔡焕杰，王 健，等. 2004. Hargreaves计算参考作物蒸发蒸腾量公式经验系数的确定[J].干旱地区农业研究，22（4）：44-47. [Zhao Y，Cao H J，Wang J，et al. Determination of the empirical coeff cient of Hargreaves formula in computing crop evapo-transpiration [J]. Agricultural Research in the Arid Areas，22（4）：44-47.]

Abdelhadi A W，Hata T，Tanakamaru H，et al. 2000. Estimation of crop water requirements in arid region using Penman-Monteith equation with derived crop coefficients：a case study on Acala cotton in Sudan Gezira irrigated scheme [J]. Agricultural Water Management，45（2）：203-214.

Allen R G，Pereira L S，Raes D，et a1. 1998. Crop evapotranspiration—Guidelines for computing crop water requirements - FAO Irrigation and drainage paper 56 [M]. Rome：FA.O，1-300.

Allen R O，Smith M，Pereira L S. 1994. An update for the definition of reference evapotranspiration [J]. ICID Bulletin，43（2）：1-34.

Amatya D M，Skaggs R W，Gregory J D. 1995. Comparison of methods for estimating REF-ET [J]. Journal of Irrigation and Drainage Engineering-Asce，121（6）：427-435.

Droogers P，Allen R G. 2002. Estimating reference evapotranspiration under inaccurate data conditions [J]. Irrigation Drainage System，16（1）：33-45.

Gavilán P，Lorite I J，Tornero S，et al. 2006. Regional calibration of Hargreaves equation for estimating reference ET in a semiarid environment [J]. Agricultural Water Management，81（3）：257-281.

Gong L B，Xu C Y，Chen D L. 2006. Sensitivity of the Penman-Monteith reference evapotranspiration to key climatic variables in the Changjiang （Yangtze River） basin [J]. Journal of Hydrology，329 （3-4）：620-629.

Hargreaves G H，Samni Z A. 1985. Reference crop evapotranspiration from temperature [J]. Applied Engineering in Agriculture，1（2）：96-99.

Jensen M E，Burman R D，Allen R G. 1990. Evapotranspiration and Irrigation Water Requirements. ASCE Manuals and Reports on Engineering Practice [M]. New York：American Society of Civil Engineers，70.

Martínez-Cob A，Tejero-Juste M. 2004. A wind-based qualitative calibration of the Hargreaves ET0estimation equation in semiarid regions [J]. Agricultural Water Management，64（3）：251-264.

Saeed M. 1986. The estimation of evapotranspiration by some equations under hot and arid conditions [J]. Transactions of the ASAE，29（2）：434-438.

Sumner D M，Jacobs，J M. 2005. Utility of Penman-Monteith，Priestley-Taylor，reference evapotranspiration，and pan evaporation methods to estimate pasture evapotranspiration [J]. Journal of Hydrology，308（1-4）：81-104.

Xu C Y，Singh V P. 2002. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland [J]. Water resource management，16 （3）：197-219.

Method for calculating reference crop evapotranspiration by revised Hargreaves equation over Qinghai lake basin

LI Yue-tan1，2，LI Xiao-yan1，CUI Bu-li1
（1. College of Resources，Beijing Normal University，Beijing 100875，China； 2. College of Resources and Environment，University of Chinese Academy of Sciences，Beijing 100049，China）

Reference crop evapotranspiration （ET0），one of the important parameters in hydrologic cycle，plays an important role in estimating and predicting crop evapotranspiration，water management，establishing irrigation scheme and other practice of agricultural production. Penman-Monteith equation is an accurate approach in estimating ET0，but it is not suitable in places that can't provide so many meteorological parameters. In Qinghai lake basin，Penman-Monteith equation cannot be widely used for the lack of complete meteorological observation，so another method should be find to calculate ET0. Hargreaves equation is an alternative ET0estimation equation when only air temperature data is available. In order to enhance the appropriateness of Hargreaves equation within this area，using the meteorologic data from 1958 to 2006 of Gangcha meteorological station over Qinghai lake basin，the Hargreaves equation was revised by introducing into the humidity factor，and the modif ed Hargreaves equation was verif ed with the meteorologic data from 2007 to 2012 of Gangcha meteorological station. The results showed that the modif cation of Hargreaves equation was successful，the modif ed Hargreaves equation could be used to calculate ET0accurately over Qinghai lake basin.

mining wasteland； substrate amelioration； research status； corresponding measures

A

1674-9901（2015）01-0036-07

10.7515/JEE201501005

2014-08-19

教育部新世纪优秀人才支持计划（NCET-08-0056）；“十一五”国家科技支撑计划课题（2007BAC30B02）

李岳坦，E-mail：liyuetan@ucas.ac.cn