变式教学在小学数学中的应用探究

江苏省滨海县永宁路实验学校 左克亮

传统的数学教学中，机械训练成为教师的致胜法宝，学生绝对服从于教师的管理，通过重复演练被动接受所学知识，无形中加重了学生的负担，学生苦不堪言。在变式教学中，教师引导学生从不同的视角观察，运用不同的方法思考，从“ 变化”的现象中挖掘“ 不变”的本质，在分析现象、探求规律中培养学生灵活多变的思维品质。那么，如何在小学数学教学中实施变式教学，提高教学成效？

一、概念变式——从多视角理解概念

部分教师困囿于教材，枯燥记忆概念、机械套用公式，在教学中全无自己的思维，学生也跟从于教师，成为“ 应声虫”，毫无个性可言。教师要通过概念变式教学，引领学生从多角度理解，经历初次引入、理解和应用阶段，实现由易到难，由具体到抽象，从而抓住概念的本质属性。如在“ 垂线与平行线”教学中，教者引出，在同一平面内的两条直线的位置关系，然后出示多组示例提示平行、垂直的概念，再对“ 不相交的两条直线叫作平行线”“ 不平行的两条直线一定垂直”进行判断，结果学生错误率极高。究其原因，学生对概念的层级把握不清，平行与相交概念相对，而垂直只是相交的一个特例。对此，笔者尝次运用三个阶段，丰富学生对概念的理解。

1.引入阶段。

运用动画从生活中的实物抽象出几种不同的直线关系。

2.定义阶段。

（1）自主操作，探索特性。学生在画一画、摆一摆、折一折的操作过程中，初步建立了“ 不相交的两条直线互相平行”的概念。

（2）教师反问，引发思考。教师在学生初步结论的基础上提问：“ 不相交的两条直线一定平行吗？”学生经过思考讨论，从立交桥等生活中的立体几何图形中捕捉实例。

（3）出示图形，深化理解。教师出示长方体模型，让学生思考：“ 直线m 与直线n是否平行？”经过思考，学生发现还有一个“ 隐藏”的面。

3.巩固阶段。

教师出示复杂的图形，让学生找出相互平行、垂直的直线。

二、过程变式——层层递进，步步深入

1.基本图形构造。

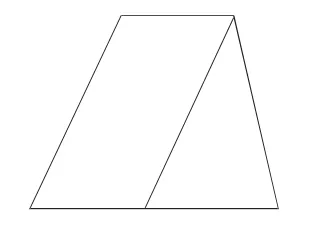
平面几何中的基本图形有线段、角、三角形、平行四边形、长方形、正方形、梯形等，通过图形变换将未知的概念纳入已知的经验系统，能帮助学生建立未知图形与已知图形之间的联系，从而对未知的概念形成认识。如在认识梯形教学中，（1）教者将等底等高的平行四边形、三角形与之放在一起，让学生猜想：他们的面积谁大谁小。（2）教者引领学生通过分割、拼补、割补等方法，将梯形转化为熟知的图形。梯形可以看成是将在一个三角形的基础上剪去一个小三角形；也可以看成是在长方形的基础上剪去一个三角形（或一个梯形）。如将梯形分割成一个平行四边形+一个三角形，不难推导出梯形的面积：（上底+下底）×高÷2。（3）通过想象获得变式图形。在掌握基本梯形的面积公式后，教师可据此提出问题：“ 根据（5+9）×6÷2这个算式，你能想象它还能是个什么样的梯形吗？学生通过想象还得出了两个特殊的梯形：直角梯形、等腰梯形。教师让学生在FLASH动画上操作，将梯形的上底逐步缩小，直至变成三角形，梯形的面积公式变为三角形的面积公式；而将上底拉长，当与下底等长时，就变成平行四边形。

2.问题情境变式。

教者在基于学生已有知识经验的基础上，创设问题情境，在已知与未知的问题之间搭建桥梁，让学生产生强烈的求知欲望。部分教师在创设问题时，较少考虑学生的认知水平，设计的问题过难，学生经思考、合作交流而不得其解，往往会丧失学习兴趣。如在“ 求一个数比另一个数多（少）百分之几”教学中，学生往往具有多几倍的解决经验，而对多（少）几分之几时难以实现知识的迁移，教者针对此，采取情境变式层层推进。

如，瑞士莲巧克力原价20 元，现价25 元，德菲丝巧克力原价25 元，现价30元，请比一比，看哪种巧克力涨得多？学生乍看，产生怀疑“ 不都是涨4 元吗？ ”从而引发认知冲突，经过讨论发现，涨价幅度不是进行涨多少的绝对比较，而要通过百分比进行比较，即瑞士莲的涨幅是5 元，是在20 元的基础上涨了，因而幅度应该是（25-20）÷20×100=25%，同样，德菲丝的涨幅应该是20%。教者将复杂的问题分解成一个个子问题，通过比较涨价的具体量——涨价幅度——比原价多百分之几，通过问题情境的递进，引导学生逐步解决多百分之几的问题。

3.数学活动变式。

教师不能生硬地将结论教给学生，而要引领学生通过观察、操作、猜想、验证等活动，让他们在亲历活动的过程中，体验知识的发展过程。如在探求三角形的三边关系教学中，教者教给学生1cm、2cm、3cm、4cm、5cm、6cm长的小棒，让学生拼成三角形，在拼的过程中填写表格，让学生根据“ 围成”与“ 围不成”的情况作出猜想：三角形的两边之和大于第三边。

总之，我们数学教师要通过变式教学，让学生学会挖掘隐含条件，明晰思路，通过操作、猜想、验证等活动，提高分析和解决问题的能力。