基于差分进化算法的多用户OFDM自适应资源分配

祝杨坤,达新宇,张亚普

（空军工程大学信息与导航学院 西安 710077）

1 引言

正交频分复用（orthogonal frequency division multiplexing,OFDM）是一种能够有效减缓宽带无线系统频率选择性影响的先进高速率传输技术，它将整个频率选择性衰落信道转换成为多个并行的窄带平坦衰落子信道，将自适应技术用在转换后的并行子信道中，可以根据子信道的瞬时特性动态地进行系统资源优化分配，能够有效地提高通信系统的抗噪声性能和频谱效率。

多用户OFDM自适应动态资源分配主要有两类优化技术：功率自适应（power adaption,MA）[1]和速率自适应（rate adaptive，RA）[2，3]。RA技术的分配算法主要有两种：系统传输速率最大化算法和保证用户公平性的算法。目前有很多文献对多用户OFDM资源分配进行研究，试图解决RA问题，然而大多不能在用户公平性和整个系统传输速率最大化之间取得很好的折中。参考文献[3]将子载波与功率分配分为两步一次执行，较好地解决了用户的公平性问题，但总的传输速率有所下降；参考文献[4]提出一种非迭代算法放松了用户速率公平性的约束限制，以牺牲速率公平性获取了系统复杂度的降低；参考文献[5]采用约束条件松弛技术,将动态资源分配问题转化为凸优化问题求解，通过追求最大的系统效应来实现系统传输速率的最大化；参考文献[6]提出一种采用多用户分集增益，通过合理选择用户的接入时刻，从而达到在保证用户公平性的同时提高了系统容量的资源分配算法；参考文献[7]利用对偶分解方法将多业务资源分配问题分解为若干独立子问题，分别得到了最优资源块与最优功率分配规则；参考文献[8]将认知OFDM中下行链路的功率分配问题，建模为一个约束优化问题，提出一种基于免疫克隆的求解方法；参考文献[9]研究了基于鱼群算法的OFDMA自适应资源分配，采用一种新的子载波分配方式，并根据改进的自适应鱼群算法进行功率分配，在实现总的传输速率最大化的同时较好地保证用户公平性，但鱼群算法在每次寻优过程中都需要执行几种行为，因此算法复杂度较高。

本文研究采用差分进化（differential evolution,DE）算法[10]解决多用户OFDM自适应资源分配中的速率自适应问题，并将资源分配问题分为子载波分配和功率分配问题来解决，最终在保证用户公平性的同时实现系统总的传输速率最大化。

2 系统模型

在多用户OFDM自适应资源分配系统中，考虑系统收发端已知信道状态信息，假设系统中共有M个用户共享N个子载波，自适应分配算法的目标是在功率Ptotal的约束下，在保证用户公平性的同时，优化子载波和功率分配方案，实现系统总传输速率的最大化。

根据参考文献[3]，可以将子载波和功率分配优化问题数学模型表示如下：

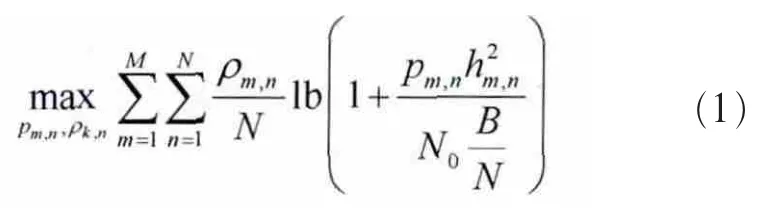
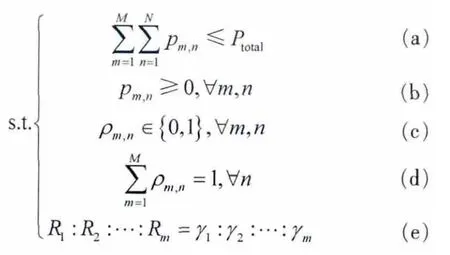
其中，N0是加性高斯白噪声（AWGN）的功率谱密度，第m个用户在第n个子载波的功率与信道增益分别为pm,n、hm,n，B为总信道带宽，ρm,n用来判断子载波n是否分配给用户m，若是，则为1，否则为0，该参数限制了每个子载波只能供一个用户使用。 是为确保用户公平性而预先设定的一组比例公平系数值，定义公平性参数F[11]为：

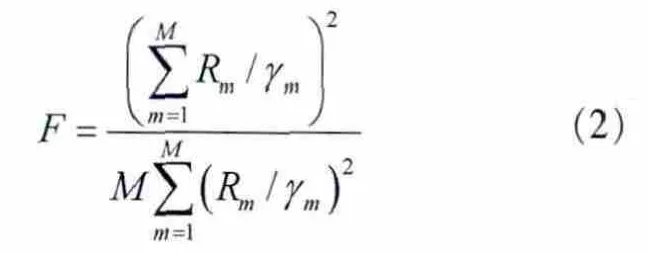
可以看出，F≤1，且F越接近1，系统公平性越好。

3 自适应资源分配算法

理论上，期望对多用户子载波和功率进行联合分配获得最优解，但由于多种约束条件的限制导致联合分配方案复杂度极高，因此考虑将子载波与功率分开进行优化分配，先进行子载波分配，然后根据分配好的子载波进行功率分配以获得最优结果。

3.1 子载波分配算法

本节进行的子载波分配基于参考文献[2]的次优子载波分配算法，C为矩阵M×N，矩阵中元素为ρm,n，表示子载波的分配情况，算法流程如下。

（1）初始化

用户速率Rm=0,各用户等功率分配，功率pm=Ptotal/M，C为全0矩阵，为M×N矩阵，用户的子载波分配集合Ω=，子载波集合A={1,2,…,N}，K为1×M的全0矩阵，表示各用户分配的子载波数目。

（2）每个用户分配信道增益最好的子载波

For m=1 to M

Cm,n=1，=0，Ωm=Ωm∪{n}，A=A-{n}，K(m)=K(m)+1，更新Rm。

（3）根据比例公平系数分配剩余子载波

While A=

寻找m满足min(Rm/γm)；

Cm,n=1，||=0，Ωm=Ωm∪{n}，A=A-{n}，K(m)=K(m)+1更新Rm。

（4）记录分配结果

子载波分配结果为C，用户的子载波分配集合为Ω={Ω1,Ω2,…,ΩM}，用户分配的子载波数目为K。

以上次优子载波分配算法的分配原理是让每个用户尽可能地使用具有最好信道增益的子载波，每次迭代时，由具有最低比例速率的用户优先选择子载波，这种分配方式在子载波分配过程中尽可能地保证了用户间的公平性。在功率分配过程中为降低系统复杂度，初始化时先进行等功率分配，获得粗略的分配结果，然后在下一步的功率分配中采用相应算法，在维持比例公平性的前提下尽可能地获得最大的传输速率。

3.2 基于差分进化算法的功率自适应分配

近年来，优化算法用于求解各种工程的最优化问题，受到人们的广泛重视，并在诸多工程领域得到迅速推广和应用。智能优化算法作为一种具有很强自适应性和自组织性的启发式搜索算法，不需要提供额外的初始点及优化目标函数的梯度信息，降低了初始条件的硬性要求，为研究无线通信中资源分配问题提供了新的契机。差分进化算法是一种基于群体差异的高效并行搜索的新兴进化算法，它采用概率转移规则，不需要确定性的规则。因此，相比于遗传算法、粒子群算法，其具有良好的求取全局极值能力,并具有结构简单、易实现、可调参数少、顽健性强等优点。本节将基于差分进化算法进行功率自适应分配，目的是使整个系统在满足用户公平性的同时达到传输速率最大化。

如式（1）所示，功率分配优化问题为非线性约束优化问题，在采用DE算法寻优时，必须考虑到优化问题的非线性约束条件，因此，需要对原始的DE算法进行相应的改进，以满足式（1）中的条件。其中约束条件（c）、（d）已通过子载波分配算法满足，条件（e）可以通过式（1）、式（2）联合满足，而条件（a）、（b）在寻优算法中需要单独设置改进措施来满足。

算法基本流程如下。

（1）个体编码

根据先前每个用户分配的子载波情况，对每个用户所分配的子载波进行功率初始化，每个用户为一个长度为K（m）的一维数组pm,i，K（m）为该用户分配的子载波数，每个用户的功率分配情况pm=(pm,1,pm,2,…,pm,K(m))，初始元素可以用如下随机方法产生：

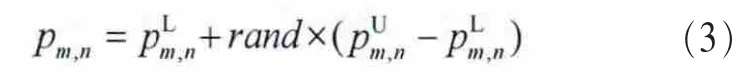
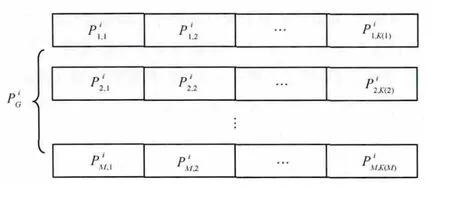
图1 编码方案

对于产生的个体，需要满足约束条件（a）、（b），由式（3）可知，约束条件（b）自然满足。因此，为满足条件（a），设置约束条件检测改进步骤，即在个体生成后，将每个用户分配的功率记入1×M的矩阵中，分配后总功率为PT，若PT>Ptotal，即分配结果不满足约束条件（a），则寻找m满足max(P(m))，令P(m)=P(m)-(PT-Ptotal)，再将P(m)等功率分配到第m个用户的相应子载波上。

（2）产生群体

重复Np次步骤（1），即可得到随机生成的Np个个体，获得初始群体。

（3）变异

DE算法和其他进化算法的主要区别是变异操作，也是产生新个体的主要步骤，该操作的基本原理是将一个差分向量加到一个基向量上去，变异操作后得到中间个体记为Vi,G+1，即：

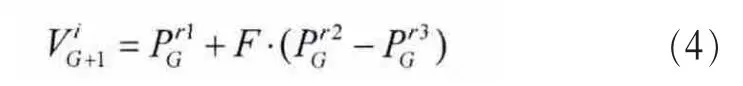
其中，r1,r2,r3∈{1,2,…,Np}且r1≠r2≠r3≠i，F∈[0,1]为一常数，称为变异因子，它控制着差分向量的幅度，F值越大算法的收敛速度越慢。

由于变异操作会导致个体中分配功率的变化，因此每个个体的变异操作结束后都需要执行一次约束条件检测改进步骤，以满足功率分配的约束条件。

（4）交叉

其中，i=1,…,Np，m=1,…,M，rnbr(m)是[1,M]范围的一个随机整数，用来保证候选个体至少从中取到某一用户的功率分配矩阵，rand∈[0,1]是一个均匀分布的随机数，交叉因子CR∈[0,1]决定了中间个体分量值代替目标个体分量值概率。

交叉操作通过杂交个体间的某功率分配矩阵，来增加种群的多样性，这种操作会造成个体总功率的改变，因此同样需要执行约束条件检测改进步骤，以满足功率分配的约束条件。

（5）选择

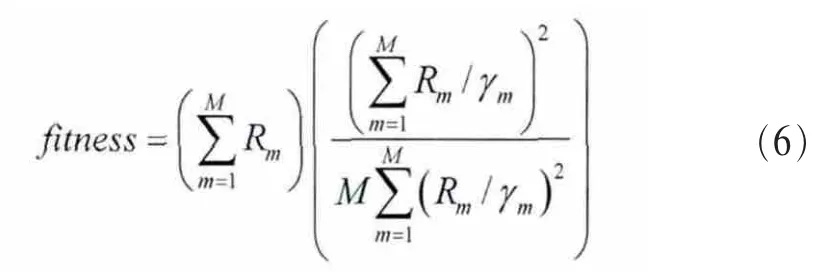
其中：

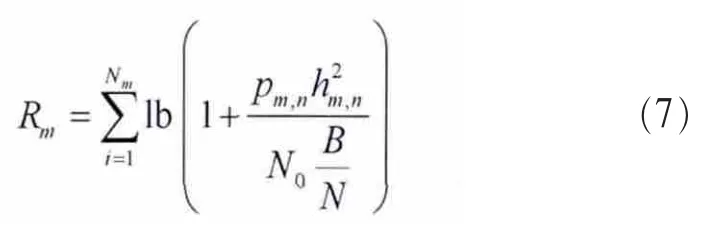
根据式（6）决定是否在下一代中用候选个体替换当前目标个体。

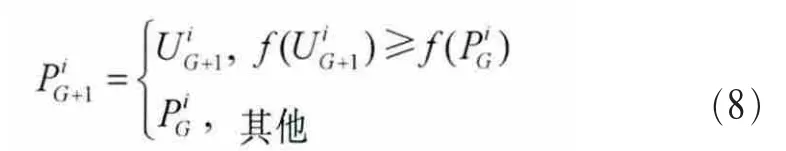
（6）记录最优值

在算法执行中引入公告板，将每一代选择操作后得到的最优状态及最优结果记录在公告板中，当G次迭代结束后，根据公告板中记录内容，选择最优状态与最优结果作为寻优的最终结果。

4 仿真结果

4.1 仿真参数设置

在仿真中，采用6径衰落信道进行信道建模。总的可用带宽B=1 MHz，分为N=64个子载波。总的发射功率Ptotal=1 W，AWGN的功率谱密度为-80 dB·W·Hz-1。仿真中假设用户的传输速率要求相同，即R1∶R2∶…∶Rm=1∶1∶…∶1。本文采用DE算法解决自适应资源问题，设置DE算法参数为：变异因子F=0.5，交叉因子CR=0.5，种群个数Np=50，最大迭代次数Gmax=100，蒙特卡洛仿真次数为100次。

4.2 性能分析

图2对比了用户数K在2～12变化时本文算法与Shen算法、Wong算法以及参考文献[8]基于AFSA的资源分配算法的系统容量。由图中可明显看出，随着用户数目的增加，本文提出的分配算法可获得比Shen算法、Wong算法更高的系统容量，容量提升约0.1 bit/s/Hz，但略低于采用AFSA进行资源分配的系统容量，约为0.04 bit/s/Hz。

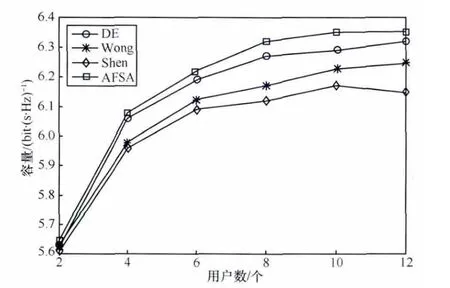
图2 系统容量随用户数变化曲线

图3 为用户数M=8，各用户的速率比例系数为1∶1∶1∶1∶1∶1∶1∶1时，本文算法与Shen算法、Wong算法及基于AFSA的资源分配算法的各用户系统容量比较。从图中可清晰地看出，Wong算法的用户公平性没有得到应有的保证，且用户系统容量较低；Shen算法虽然基本上保证了用户速率的公平性，但各用户系统容量较低；本文算法和基于AFSA资源分配算法都可以较好地保证用户速率的公平性，各用户系统容量得到一定提升，并且较为相近。

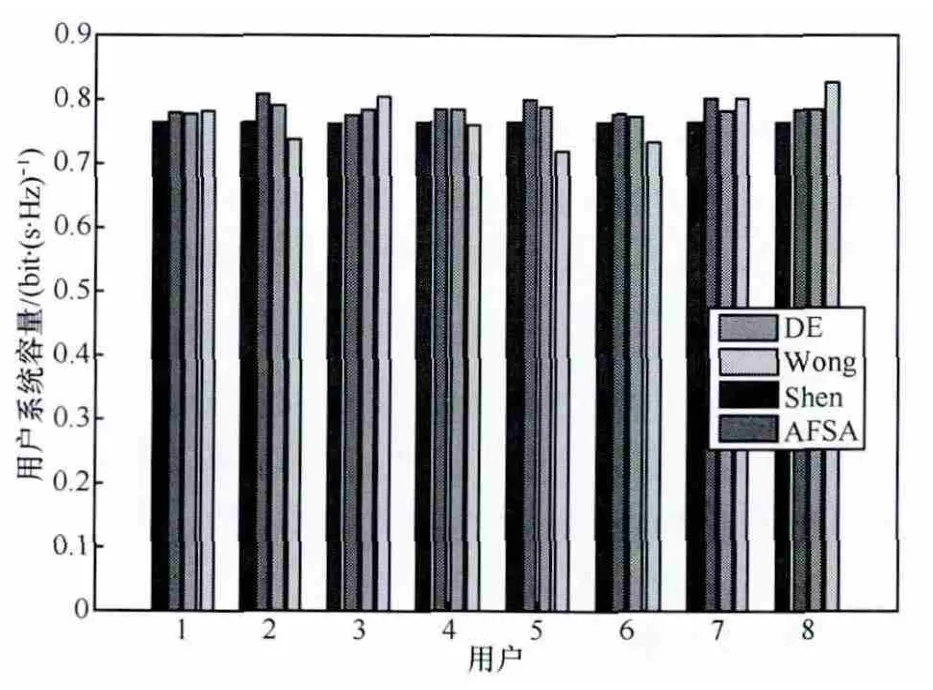
图3 用户数为8时各用户的系统容量

图4显示了4种算法在各用户的速率比例系数为1∶1∶1∶1∶1∶1∶1∶1时的比例公平性。由图中可以看出，Shen算法的比例公平性最好，参数值接近于1；Wong算法虽然提升了系统容量，但其比例公平性最差；当用户数目较大时，AFSA算法的比例公平性与Shen算法有明显差距；由前文分析可知，本文算法虽然系统容量略低于AFSA算法，但比例公平性接近于Shen算法，与Shen算法相比，比例公平性参数值仅差0.003左右。

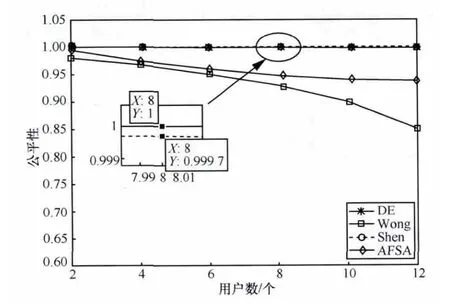
图4 各算法的比例公平性

综合以上可知，Shen算法通过采用迭代搜索方法较好地实现了用户公平性，但系统复杂度较高且容量较低；Wong算法采用非迭代算法放松了用户公平性的约束限制，以牺牲公平性获取复杂度的降低和较高的系统容量；AFSA算法在子载波分配过程中松弛了约束条件，降低了用户间的公平性，在功率分配过程中将用户公平性与系统容量综合考虑作为优化目标函数来弥补降低的公平性，并最大化系统容量，从图2～图4的对比结果可以看出，AFSA算法虽获得高于其余算法的系统容量，但松弛条件降低了用户公平性，并且鱼群算法寻优过程的多种行为带来了较高的系统复杂复杂度；本文算法由于全面考虑分配过程中的约束条件，并且采用复杂度较低的DE算法，在获得较优公平性的同时，获得较高的系统容量，体现了本文算法的优越性。

4.3 算法复杂度

由上节可知，本文算法与参考文献[8]的算法均可以在保证用户速率公平性的前提下，获得系统容量较大的提升，本部分将对采用的DE算法与采用AFSA算法的计算时间复杂度进行分析比较。

两种算法在资源优化分配中都采用了将子载波与功率分步进行的分配策略，因此在分析复杂度时，也应当将子载波分配与功率分配分开计算复杂度。首先，对两种算法的子载波分配进行复杂度分析，已知用户数为M，种群个体数为N，由分配方案可知，两种算法的子载波分配方案复杂度均为O(MNlbN)；其次，对两种算法的功率分配方案进行分析，根据对两种群智能算法的描述可知，假设最大迭代次数为G，每个个体迭代一次需要的运行时间为TT，则可以得出群智能优化算法进行优化结束后所需要的总运行时间为N×G×TT。

对于AFSA算法，一个人工鱼个体的更新需要并行执行4种行为，分别为觅食行为、追尾行为、聚群行为和随机行为，觅食行为、追尾行为、聚群行为所需要的运算为：4次乘法运算，4次加法运算；随机行为所需要的运算为：1次乘法运算，1次加法运算。假设乘法与加法运算时间分别为Tm与Ta，由于觅食行为执行时还存在try_number次的尝试迭代，因此AFSA算法完成优化所需的平均时间为：

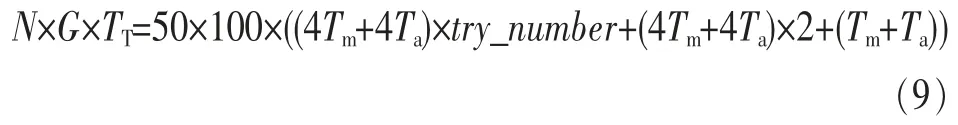
对于本文采用的DE算法，一个个体的更新执行变异、交叉操作以及为满足功率约束条件所设置的改进步骤，变异操作所需要的运算为1次乘法运算和4次加法运算；交叉操作所需要的运算为2次加法运算，因此本文算法完成优化所需的平均时间为：

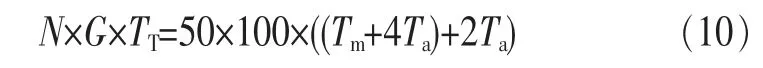
对两种算法设置的参数如下：最大迭代次数G=100，种群N=50，AFSA算法中尝试次数try_number=20，对两种算法的性能进行简要对比记录，见表1。

表1展示了两种资源分配算法的各种性能对比情况，可以看出，两种算法的子载波分配算法复杂度相同，当用户数为8时，在保证用户比例公平性的同时，本文算法的系统容量比基于AFSA的资源分配算法的系统容量低约0.01 bit/s/Hz，但其功率分配运算的复杂度仅为AFSA分配算法的4%，证明了本算法的高效性。

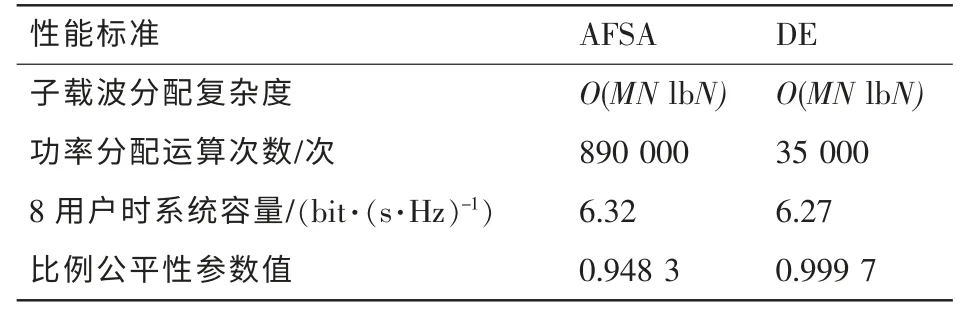
表1 两种算法性能对比概况

5 结束语

本文提出一种采用改进的差分进化算法解决多用户比例公平性约束条件下的速率自适应资源分配问题，将资源分配问题分为两步执行，先进行有效的子载波分配，然后根据已分配子载波情况采用改进的差分进化算法，兼顾系统容量最大化与用户公平性进行功率分配。仿真结果表明，本文算法很好地解决了速率自适应资源分配问题，在实现低复杂度下系统容量最大化的同时保证了用户间的公平性，是一种有效的兼顾系统容量和用户公平性的自适应资源分配算法。

1 Wong I C,Evans B L.Optimal downlink OFDMA resource allocation with linear complexity to maximize ergodic rates.IEEE Trans on Wireless Communications,2008,7(3):962～971

2 Mohanram C,Bhashyam S.A sub-optimal joint subcarrier and power allocation algorithm for multiuser OFDM.IEEE Communications Letters,2005,9(8):685～687

3 Shen Z K,Andrews J G,Evans B L.Adaptive resource allocation in multiuser OFDM systems with proportional rate constraints.IEEE Transactions on Wireless Communications,2005,4(6):2726～2737

4 Wong I C,Shen Z K,Evans B L,et al.A low complexity algorithm for proportional resource allocation in OFDMA systems.Proceedings of IEEE Signal Processing Systems,USA,2004

5 Huang J W,Subramanian V G,Agrawal R,et al.Downlink scheduling and resource allocation for OFDM systems.IEEE Transactions on Wireless Communications,2009,8(1):288～296

6 薛晓洁,赵林靖,刘鹏等.一种新型的多用户OFDM系统资源分配策.电子学报,2007,35(6A):64～68 Xue X J,Zhao L J,Liu P,et al.A novel resource allocation algorithm in multiuser OFDM system.Chinese Journal of Electronics,2007,35(6A):64～68

7 左勇,刘学勇,刘海洋等.基于对偶分解的OFDMA系统资源分配算法.电子与信息学报,2012,34(12):2843～2849 Zuo Y,Liu X Y,Liu H Y,et al.A dual-decompostition-based resource allocation algorithm for OFDMA systems.Journal of Electronics & Information Technology,2012,34(12):2843～2849

8 柴争义,陈亮,朱思峰等.认知无线网络中基于免疫克隆优化的功率分配.电子科技大学学报,2013,42(1):36～40 Chai Z Y,Chen L,Zhu S F,et al.Power allocation of cognitive wireless network based on immune clonal optimization.Journal of University of Electronic Science and Technology of China,2013,42(1):36～40

9 汪照,李有明,陈斌等.基于鱼群算法的OFDMA自适应资源分配.物理学报,2013(12)Wang Z,Li Y M,Chen B,et al.OFDMA adaptiue resource allocation based on fish swarm algorithm.Acta Physica Sinica,2013(12)

10 Das S,Suganthan P N.Differential evolution:a survey of the state-of-the-art.IEEE Transactions on Evolutionary Computation,2011,15(1):4～31.

11 Schwarz S,Mehlfuhrer C,Rupp M,et al.Throughput maximizing multiuser scheduling with adjustable fairness.Proceedings of IEEE InternationalConference on Communications,Kyoto,Japan,2011