基于拍卖博弈的可重构服务承载网动态构建算法
梁宁宁,兰巨龙,程国振,杨 琴
(1.国家数字交换系统工程技术研究中心 郑州450002;2.78006部队 成都610066)
1 引言
随着网络业务形态的不断丰富、应用规模的不断扩大,互联网为人类工作生活提供了便利。然而,由于当前IP承载模式的简单僵化、功能单一,基础网络所能提供的服务与业务需求之间的差距日趋显著[1]。
基于此,可重构信息通信基础网络体系将底层网络与服务提供在逻辑上相分离,底层网络为承载网提供网络资源,可重构信息通信基础网络为用户提供定制服务,而网络服务的提供主要通过为用户构建服务承载网的方式实现[2]。可重构服务承载网(reconfigurable service carrying network,RSCN)优先考虑业务需求与网络拓扑、资源状态等条件,构建出多个在底层物理资源上存在交集,能够提供不同服务能力的承载子网,如图1所示。

图1 可重构服务承载网示意
服务承载网的构建是指依据某种约束条件,将业务需求映射到底层网络的相应物理路径,并在路径上分配带宽的过程。其本质是底层资源分配问题。现有服务承载网构建存在以下两个问题:首先,现有构建方法一般假设不同业务并发地申请有限的底层资源,业务之间相互隔离,忽略了业务间的竞争;其次,现有服务承载网构建算法一般是在底层网络拓扑变化(底层节点或链路失效)或者新到达请求被拒绝时执行重映射,没有涉及不同业务场景下的动态构建措施。
在不同业务对有限的底层网络进行共享时,如何根据业务需求建立服务承载网,并实时感知业务变化,动态调整服务承载网的构建,以期实现整体系统的利益最大化,这是本文要讨论的问题。
为解决上述问题,本文提出了一种基于拍卖博弈的可重构服务承载网动态构建 (dynamic auction game-based reconfigurable service carrying network construction,DAGR)算法,以拍卖机制为基础,设计简单的定价方式,降低系统的附加处理和计算负担。引入合作博弈理论并进行周期映射,在最大化承载网总体构建收益的同时,减少系统开销。具体过程如图2所示。首先各业务提出自身的构建需求,由基于拍卖的定价机制计算各业务需支付的费用,并返回业务,然后对于确定加入网络的业务,引入以最大化系统效用为目标的合作博弈理论构建服务承载网,对底层资源进行分配。

图2 基于拍卖博弈的可重构服务承载网架构
2 相关研究
当前有关服务承载网构建的研究主要集中在资源分配和网络映射等方面[3~7]。参考文献[8]以负载均衡为目标,首先将虚拟节点映射到距离已映射虚拟节点较近且负载最轻的底层节点上,而后使用最短路径算法映射虚拟链路,并根据底层网络资源状况对承载网进行重映射。参考文献[9]提出了节点与链路同时考虑的一步映射算法,然而由于该算法是基于分布式的,在性能和最优性方面都与集中式存在差距。且算法没有动态考虑构建请求的生存时间,即为已允许的构建需求所分配的资源将持久分配,这对新进请求的加入造成限制。参考文献[10]提出了一种协调节点和链路映射的数学规划。使用虚拟节点地理位置作为启发式信息减少搜索空间,将造成热点问题。且映射方案基于简单经济模型构建,其定价/花费是线性函数,没有提供能够最大化底层网络的承载网构建请求之间的竞争机制。
为了提高服务承载网请求接受率,最大化成本收益,博弈论也日益受到研究者的关注。参考文献[11]设计了一种分布式算法,以实现数据中心网络中有效公平的带宽分配。算法通过调整基础带宽,为云提供者提供了公平共享与最小数据保障之间的均衡折中。参考文献[12]针对视频数据爆发性增长,提出了一种整数规划算法;并通过综合考虑视频片段的大小和流行分布,提出了一种快速贪婪的方法解决这一NP难问题。参考文献[13]引入博弈论,提出了一种解决服务器上视频需求瞬间拥挤的迁移方法。但是,以上算法仅针对视频需求,并未建立承载网构建的一般模型。参考文献[14]以底层节点和链路作为参与者,通过构建合作博弈模型进行承载网映射。然而,算法将节点映射与链路映射相分离,分别进行博弈模型构建,而后将两个博弈进行嵌套,增加了算法复杂度。
基于此,本文提出了一种基于拍卖的周期映射承载网构建算法。算法通过构建合作博弈模型,最大化承载网整体构建效益。通过周期映射,将时间周期内的业务请求聚类,在最大化构建收益和最小化构建请求与建立的等待时间之间进行平衡。
3 问题描述
3.1 底层资源
构建底层资源模型,将底层物理网络抽象为无向图Gs=(Ns,Ls,Cs),其中,Ns和Ls分别代表底层网络中节点和链路的集合,Cs代表底层资源,即底层物理网络所能提供的能力。底层资源通常包括节点资源和链路资源。其中,节点资源包括节点CPU和内存容量,链路资源则主要指带宽资源。同时,引入链路资源单位花费Clink和节点资源单位花费Cnode。
3.2 业务需求
RSCN业务需求模型可表示为无向图Gr=(Nr,Lr,Rr),其中,Nr和Lr分别表示RSCN中虚拟节点和虚拟链路的集合,分别是Ns和Ls的子集,RSCN构建请求通常包含对底层物理节点和链路的约束,用Rr代表对虚拟节点和虚拟链路的需求,包括虚拟节点的计算资源需求和存储资源需求,虚拟链路的带宽资源需求及时延需求。
同时,业务需求中还包括每个业务构建服务承载网的请求函数,包括愿购买资源量、愿出价格及使用时间等。
3.3 服务承载映射
RSCN构建问题可以表述成满足Gr中约束条件Rr的由Gr到Gs子集的一个映射,表示如下:

其中,Nv奂Ns,Lv奂Ls,Gv表示构建RSCN的底层物理网络的服务能力。RSCN构建可以分割成节点映射和链路映射。
节点映射:
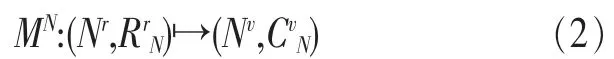
链路映射:
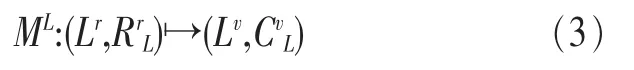
其中,RrN和RrL分别表示RSCN构建中对虚拟节点和虚拟链路的限制条件,CvN和CvL分别代表构建RSCN的底层资源情况,即底层物理节点和链路所能提供的服务承载能力。
3.4 服务承载网构建目标
(1)底层资源最大化利用
构建服务承载网的初衷即在存在交集的多个物理资源上,提供具有不同服务能力的承载子网,对于有限的底层网络,最大化底层资源利用,最大化总体构建收益即服务承载网的构建目标。因此,定义承载网整体构建收益如下:
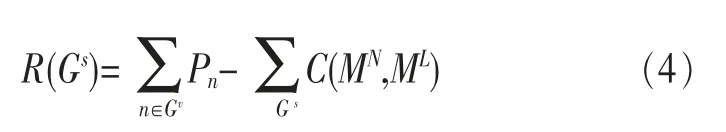
(2)周期性映射
在服务承载网映射中,构建请求通常不会按照某种特定规律的时间间隔到达,本文算法提出周期映射的方式。将某一时间周期到达的服务承载网构建请求聚类处理,而后针对不同业务类型进行映射,既减少了系统开销,又最优化了构建收益。定义时间周期为T,则服务承载网构建请求集合为Gr(T)。
4 博弈论模型的构建
对于每个提出服务承载网构建请求的业务,构建的服务承载网为其分配相应的底层资源,而其终极目标即最大化系统总体效用,试图使每个业务相互合作,形成合作博弈模型。这里假设业务都是按照自己的需求真实上报,并不存在谎报的情况。
4.1 模型要素
(1)参与者
定义业务为博弈参与者,用N={1,2,3,…,n}表示。
(2)策略
构建博弈的策略集合C={Bw,Dl,Cbm,CPcpu},其中,Bw表示链路带宽,Dl表示时延需求,即业务提出的相应的链路需求;节点需求分别由Cbm和CPcpu表示,Cbm为缓存容量(buffer memory capacity),CPcpu为CPU计算能力(CPU calculate power)。
(3)效用函数
效用函数定义为最大化服务承载网构建整体收益,即由业务的支付总和减去满足业务需求所构建服务承载网的花费的“净收入”,即:

那么,最大化整体收益问题可以表示为:

其中,式(7)表示构建请求出价大于底层资源损耗;式(8)表示所选路径时延小于构建请求的时延需求;式(9)表示当前承载的n个业务的虚拟节点消耗的缓存资源之和小于节点最大缓存容量;式(10)表示当前承载的n个业务的虚拟节点消耗的CPU计算资源之和小于节点最大CPU计算能力;式(11)表示当前承载的n个业务的虚拟链路消耗的带宽资源之和小于链路的最大带宽。
4.2 定价机制
现有定价机制主要包括针对特定用户、协商及拍卖等。针对特定用户的定价,一是缺乏普适应,二是增加系统开销;协商定价需要服务提供方与业务就价格反复商议,直到达成共识,其收敛时间较长,系统开销大;而拍卖定价机制只需业务向服务提供方提出所需资源及支付意愿,服务提供方据此进行服务承载网构建,分配底层资源并收费。当然,其前提条件是提出构建服务承载网需求的业务真实地表达了自身的业务需求。因此,本算法基于拍卖机制定价。
4.2.1 业务需求函数
所谓业务需求函数qn(Pn,tn),是在使用时间tn内,业务n愿意为所需资源qn支付的价格Pn。本文定义业务需求函数中的参数包括:愿出价格、购买资源量、资源使用时间,表示为
4.2.2 拍卖规则
假设在某一周期T,n个业务提出构建服务承载网的请求,竞争总量为Q的底层资源,已知在不同的资源价格Pn下,业务n愿意购买资源qn。首先根据各业务的出价确定周期T内的单位资源价格:

式(12)表示,在满足n个业务构建总需求不大于底层总资源量Q的情况下,将n个业务中单位资源价格的最大值作为周期T内的单位资源价格,由此可得:
业务n可分得的资源qn(T)为:

业务n需为此支付的费用cn为:

4.2.3 拍卖规则性质
当业务的出价qn(Pn,tn)是真实的,由式(12)所得为市场出清价格,这将使资源配置达到最优,即当所有参与者都已知业务数量n和资源总量Q时,且Q不变,则在拍卖结果中存在Nash均衡[15]。即若参与的某业务有意压低报价,将导致服务承载网构建的整体效益降低。
实际情况中,n和Q不可能成为所有业务的公共知识,对业务而言,n和Q是不确定的,这就迫使业务要真实的表达自身需求。同时,在网络条件下,业务对底层网络的信息优势受到抑制,这也促使业务要“讲真话”。
4.2.4 拍卖中存在的问题
算法采用的拍卖机制是周期性的。在不同周期T,资源价格是变化的。然而对于跨越几个计费周期的业务而言,按照各周期的资源价格进行收费显然是不现实的,这将给业务造成超出预算的风险和负担。因此,算法规定,单位资源价格以业务加入网络时为准,其生存时间内,不随周期性的拍卖机制变化。但当前生存周期结束,再次请求资源时,就需按当时的单位资源缴费。
4.3 基于拍卖博弈的服务承载网动态构建模型DAGR
假设时间周期T内,到达了n个业务的服务承载网构建请求,每个构建请求提交信息分别包括使用时间tn、资源需求qn和愿付价格Pn。由拍卖机制确定业务需要为此支付的费用cn,并将其反馈给相应业务。对于接受费用的业务请求构建请求集合,进行服务承载网构建。
在服务承载网映射中,首先将业务请求构建为集合Qn,并按照业务类型将其聚类为Qi。收集底层网络资源信息,计算得到满足业务需求的所有可行路径集合,将各条路径代入式(5),得到最优路径及最优带宽,至此,将Qi映射到满足其业务需求的底层网络,完成服务承载网构建。算法流程如图3所示。

图3 基于拍卖博弈的可重构服务承载网构建流程
5 实验仿真
为评估算法的效能,本文将与基于简单经济模型并协调节点与链路映射的ViNEYard[10]算法和以负载均衡为目标的G-SP[8]算法进行性能比较。
5.1 实验环境构建
仿真实验中的基础网络拓扑由BRITE工具随机产生的150个节点组成,节点连接率为0.5,节点与链路资源服从50~100的均匀分布。RSCN节点个数需求满足2~10的均匀分布,链路带宽需求、节点CPU能力及缓存容量均服从0~30的均匀分布,节点连接率为0.5。业务请求构建RSCN的到达过程服从时间单位为100、强度为10的泊松过程;每个RSCN的生存时间服从期望值为1000的指数分布。映射周期为一个单位时间T。假设各业务构建请求单位资源出价服从1~3的均匀分布,而底层节点单位花费和链路单位花费相等且均为1。并假设只要通过拍卖机制后的单位资源价格不高于该业务出价的两倍,业务都可接受。为了仿真结果的准确性,本文共进行仿真实验20次,所取结果为所有实验结果的平均值。
5.2 服务承载网构建总收益

图4 服务承载网构建总收益
图4 所示为10个周期T内,不同算法构建服务承载网的总收益。可以看出,DAGR算法较之其他算法,能带来更多的收益。虽然G-SP算法以负载均衡为目标,但在进行服务承载网映射时,将节点映射与链路映射分两阶段处理,大大限制了方案空间,因此总收益比同时考虑节点和链路映射的ViNEYard算法略低。而基于拍卖机制的DAGR算法激发了各业务之间的竞争,比其他两种算法相应地得到了更高的构建总收益。
5.3 服务承载网构建成功率
定义1(RSCN构建成功率)RSCN已构建成功的请求个数与构建请求总数之比,即:

式(15)中,Csuccess表 示RSCN成 功 构 建 的 请 求 数,Call表示构建请求总数。如图5所示为不同时间周期内的服务承载网构建成功率。由于ViNEYard算法进行承载网映射时,将节点映射和链路映射协调为一阶段,因此,其构建成功率比采用节点、链路分别映射的G-SP算法高。DAGR算法以构建总收益为目标,存在定价时与业务的“双向选择”问题。实验中设定,业务对于超过双倍价于自己报价的定价,不予接受,基于此,在构建初期,会有部分业务主动放弃构建服务承载网的请求。因此,该算法的构建成功率在某些周期相对ViNEYard算法较低,在75%左右。
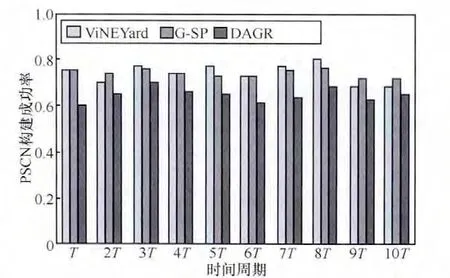
图5 服务承载网构建成功率
6 结束语
针对不同业务对有限的底层网络共享时存在的竞争问题,本文提出了一种基于拍卖博弈的服务承载网动态构建算法。算法能够根据业务需求建立服务承载网,并实时感知业务变化,动态调整服务承载网的构建,最终实现整体系统的利益最大化。
1 兰巨龙,程东年,胡宇翔.可重构信息通信基础网络体系研究.通信学报,2014,35(1):128~139 Lan J L,Cheng D N,Hu Y X.Research on reconfigurable information communication basal network architecture.Journal on Communications,2014,35(1):128~139
2 中华人民共和国科学技术部.《可重构信息通信基础网络体系研究》项目计划任务书,2011 Ministry of Science and Technology of the People’s Republic of China.Project Plan of Research on Reconfigurable Information Communication Basal Network Architecture,2011
3 Fischer A,Botero J F,Beck M T,et al.Virtual network embedding:a survey.IEEE Communications Surveys & Tutorials,2013,15(4):1888~1906
4 Gomes R L,Bittencourt L F,Madeira E R M.A bandwidth-feasibility algorithm for reliable virtual network allocation.Proceedings of IEEE 28th International Conference on Advanced Information Networking and Applications,Victoria,Australia,2014:504~511
5 Kareche S,Ductor S,Mezghiche M.A new robust heuristic for assigning substrate network resources to virtual networks.Proceedings of International Conference on Advanced Networking Distributed Systems and Applications,Bejaia,Algeria,2014:47~52
6 Chase J,Kaewpuang R,Wen Y G,et al.Joint virtual machine and bandwidth allocation in software defined network(SDN)and cloud computing environments.Proceedings of IEEE ICC,Sydney,Australia,2014:2969~2974
7 江逸茗,兰巨龙,周慧琴.网络虚拟化环境下的资源监控策略.电子与信息学报,2014,36(3):708~714 Jiang Y M,Lan J L,Zhou H Q.Resource monitoring policy for network virtualization environment.Journal of Electronics &Information Technology,2014,36(3):708~714
8 Zhu Y,Ammar M.Algorithms for assigning substrate network resources to virtual network components.Proceedings of IEEE INFOCOM,Barcelona,Spain,2006:1~12
9 He J,Zhang S R,Li Y,et al.Davinci:dynamically adaptive virtual networks for a customized internet.Proceedings of ACM CoNEXT,Madrid,Spain,2008:1~12
10 Chowdhury N,Rahman M,Boutaba R.ViNEYard:virtual network embedding algorithms with coordinated node and link mapping.ACM/IEEE Transaction on Networking,2011,20(1):206~219
11 Guo J,Liu F M,Zeng D,et al.A cooperative game based allocation for sharing data center networks.Proceedings of IEEE INFOCOM,Turin,Italy,2013:2139~2147
12 He J,Zhao X M,Zhao B H.A fast,simple and near-optimal content placement scheme for a large-scale VoD system.Proceedings of 2012 IEEE International Conference on Communication Systems(ICCS),Singapore,2012:378~382
13 Feng Y,Li B.Bargaining towards maximized resource utilization in video streaming datacenters.Proceedings of IEEE INFOCOM,Orlando,2012:1134~1142
14 Soualah O,Fajjari I,Aitsaadi N,et al.A reliable virtual network embedding algorithm based on game theory within cloud’s backbone.Proceedings of IEEE International Conference on Communications(ICC),Sydney,Australia,2014:2975~2981
15 Back K,Zender J F.Auctions of divisible goods:on the rationale for the Treasury experiment.Review of Financial Studies,1993,30(3):733~764

