导管架平台的振动响应统计分析
谢 卓,张火明,方贵盛,徐 灵
(1.中国计量学院 计量测试工程学院,浙江 杭州 310018;2.浙江水利水电学院 机械与汽车工程学院,浙江 杭州 310018)
导管架平台的振动响应统计分析
谢 卓1,张火明1,方贵盛2,徐 灵1
(1.中国计量学院 计量测试工程学院,浙江 杭州 310018;2.浙江水利水电学院 机械与汽车工程学院,浙江 杭州 310018)
海洋结构物动力特性的研究对于海洋结构物的疲劳寿命估算和疲劳损伤预测具有重要的意义.我们建立了简易导管架平台模型,对随机波激励下平台的频域振动响应进行了分析.利用莫里森方程在惯性体系下对双甲板导管架平台的载荷以及振动位移响应进行了推导计算.采用有义波高分别为15 m、20 m、25 m的Pierson-Moskowitz(P-M)波高谱对其进行研究.结果表明,在相同频率下,有义波高大的波浪对导管架平台响应的影响更大.在得到振动位移响应谱后对每个几何坐标下位移的方差以及振动位移响应的极值进行了计算与探讨.
导管架平台;随机波;振动响应
为了满足现代工业日益增长的能源需求,油气开发向海洋领域发展已成为一种必然趋势[1].海洋资源巨大的开发前景带来的不仅仅是大好的发展机遇,同时也为很多科研人员带了不少的技术难题和设计要求[2].作为海洋石油、天然气资源开发的重要基地,海洋平台的开发、研究和利用越来越受到人们的广泛关注[3].导管架式固定平台就现在而言,是最适合在近海采油的工具[4].导管架是它的主要组成部分,再加上甲板以及桩腿,应用的水深范围在10~300 m之间.工作中的导管架平台除了承受因自身重量和上部生产设施产生的载荷之外,最主要的外部载荷还是风、海浪、海流、浮冰以及地震等产生的载荷[5].
在导管架平台设计的考虑过程中,波浪力的存在至关重要,同时又十分复杂[6].在往常的计算研究中,我们常常把随机波当作一种有规律的能预测形式的波,求出波浪载荷对平台结构体的最大作用力,然后根据静力学方法计算出结构构件的应力,再结合构件的自身条件参数求出最大应力下的位移距离,评价结构的安全度[7-8].赵洲,张火明[9]采用频域计算方法和时域计算方法相结合及线性处理和非线性修正相补充的方法,对水面船舶在不规则波中的纵向大幅运动进行计算,实现了船体在十年一遇海况下的大幅运动模拟.李宁[10]对海洋平台所受的随机波浪力采用谱分析的方法进行了研究,通过提取海洋平台的一阶模态将结构简化为单自由度系统,并对海洋平台在随机波浪载荷下的动态响应进行了数值仿真计算.余建星等[11]针对在役导管架平台通过计算结构传递函数和响应谱对平台进行模态分析.在平台的设计过程中,只想到了静力效应是绝对不行的,有些特定的动力作用产生的后果,要比想象的严重,所以必须进行各方面情况下的振动响应的统计分析[12].
本文采用不同的P-M谱,通过对结构传递函数、载荷谱密度以及响应谱密度的对比求解分析,研究了有义波高对平台响应的影响以及平台响应的极值问题,并得出了一些有意义的结论,可以作为导管架平台实际应用的参考.
1 建立模型
为了简化计算,我们选取了一个结构相对简单的导管架平台进行分析,即双甲板四桩腿式导管架.然后通过计算波浪力载荷对导管架的作用,最后求出各种情况下的导管架甲板响应的最大位移.
图1、图2就是我们需要计算的简化之后的具有两层甲板的固定平台.质量全部集中在上下两层甲板,在计算时能够得到两个自由度的分析模型,固定式导管架平台的导管是研究和设计的重心,随着水深的分布,平台受载荷影响会有所不同.当然,文中并未牵涉流载荷分布,针对两层甲板而言是完全可取的.上层的质量为m1,下层的质量是m2,海底基础刚性固定,两个质量独立的位移坐标分别是y1和y2.

图2 二维模型图Figure 2 Two-dimensional model diagram
2 导管架平台的随机响应分析
莫里森方程作为计算海洋结构物上波浪力的常用方法,其计算的波浪力包括与水平速度的平方成正比的阻力项和与水平加速度成正比的惯性力项.阻力项是由于水质点的速度引起的,而惯性力项则是由于水质点的加速度引起的.其表达式可以表示为
f(t)=C1u(t)|u(t)|+C2a(t).
(1)式(1)中:C1=0.5CDρD,C2=0.25CMπD2,CD、CM—拖曳力系数和惯性力系数,D—桩柱直径.u(t)—海水质点水平速度,a(t)—海水质点的水平加速度.对(1)式积分得到整个圆柱上的波浪力.
在惯性体系中惯性系数CM和拖曳力系数CD相比,前者处于主导地位.在图2所建立的模型中4个垂直立柱和2个平行的受力支支撑承受主要的波浪载荷.惯性系中的莫里森方程可以写为
f(t)=-0.25CMρπD2a(t).
(2)

Sf(ω)=|TF(ω)|2Sη(ω).
(3)

将立柱上的波浪力处理为集中在结点1和结点2上的集中载荷即上下两层甲板的质点载荷.
计算结点1和结点2载荷分别为
(4)

(5)
根据式(5)计算频率响应函数Hk(ω):
(6)
第k个模态响应谱密度与模态载荷谱密度之间的关系为
(7)
(8)

(9)
计算位移yk的方差
(10)
3 算例分析
3.1 导管架平台参数设置
采用表1所示的平台参数进行算例分析,其中Kij为平台的刚度系数,ζ为阻尼比,Nl表示平台具有四个垂直的立柱,Nc表示平台2个受力的平行支撑.采用Pierson-Moskowitz波高谱,其谱密度Sη(ω)由式(11)计算可得.

(11)
3.2 统计响应结果
有效波高H分别为15、20、25 m时的波谱密度Sη(ω)由式(11)计算结果如图3,波高有义值25 m时谱曲线包围面积最大,15 m时最小.图4、图5分别为结点载荷谱密度的传递函数和载荷谱密度.

图3 波浪谱密度Figure 3 Spectra density of waves

图4 结点载荷谱传递函数Figure 4 Transfer functions of node load spectra
图6、图7则为计算所得的模态载荷谱密度及其模态响应谱密度.不难看出在相同频率下,H=25 m时其模态载荷谱密度和模态响应谱密度最大,H=15 m时模态载荷谱密度和模态响应谱密度最小,即相同频率下随着波浪有义波高的增大,其导致的平台甲板模态响应会更加强烈.
图8、图9为计算所得上甲板和下甲板的振动位移响应谱.经计算三种有效波高情况下,其上甲板和下甲板分别同时在频率ω为0.32 rad/s、0.29 rad/s、0.27 rad/s处达到峰值.图8和图9说明在相同频率下,有义波高大的波浪对导管架平台响应的影响更大.
采用P-M谱的式(10)积分上限和下限分别取0.16 rad/s和1.4 rad/s,计算H=15 m的自由度位移响应均方根分别为σ(y1)=0.08 m和σ(y2)=0.03 m.在实际工程应用中,振动位移响应yk的极值为±3σ(yk),由此可得上甲板的振动位移响应极值为0.24 m;下甲板为0.09 m.同样求得H=20 m时振动位移响应极值,上甲板和下甲板分别为0.298 m、0.113 m;H=25 m时,分别为0.348 m和0.132 m.这是随机波浪载荷的一个重要统计值,由此可判断如果构件的静应力和位移在极值范围内则认为结构是安全的.

图5 结点载荷谱密度Figure 5 Spectrum density of Node load

图6 模态载荷谱密度Figure 6 Spectrum density of modal load

图7 模态响应谱密度Figure 7 Modal response spectrum density
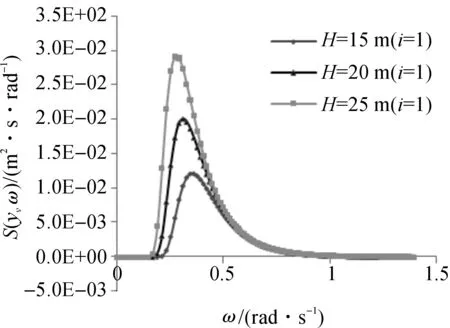
图8 振动位移响应谱(上甲板)Figure 8 Vibration displacement response spectrum

图9 振动位移响应谱(下甲板)Figure 9 Vibration displacement response spectrum
4 结 语
本研究中通过对导管架平台数学模型的分析,研究了频域下随机波对简易的双甲板导管架模型的振动影响.通过对其载荷谱和振动位移响应谱的研究分析得到以下结论:在相同频率下,有义波高大的波浪对导管架平台的影响更大.求得振动位移响应谱后对其方差和均方根也做了相应的研究,这对于海洋结构物的疲劳寿命估算和疲劳损伤预测是十分必要的.
[1] 王强.新型深海系泊缆的动力特性研究[D].杭州:中国计量学院,2012. WANG Qiang. The new deepwater mooring system dynamic characteristics research[D].Hangzhou: China Jiliang University,2012.
[2] 李世龙,吴家鸣,刘昊宇.波浪载荷作用下的导管架平台响应分析[J].海洋技术,2013.32(2):66-72. LI Shilong, WU Jiaming, LIU Haoyu. Analysis of response of jacket platform under wave loading[J].Ocean Technology,2013,32(2): 66-72.
[3] 尹彦坤,邓欣,彭绍源,等.导管架式采油平台的确定性波浪响应分析[J].广东化工,2012,39(7):210-211. YIN Yankun, DENG Xin, PENG Shaoyuan. The jacket production platform to determine the wave response analysis[J].Guangdong Chemical,2012,39(7):210-211.
[4] 刘与嘉,张宝琳.含控制时滞的海洋平台前馈反馈最优跟踪控制[J].中国计量学院学报,2014,25(1):99-106. LIU Yujia, ZHANG Baolin. Offshore platform with a feedforward control delay feedback optimal tracking control[J].Journal of China University of Metrology,2014,25(1):99-106.[5] 窦培林,王辉辉.导管架平台强度分析[J].江苏科技大学学报:自然科学版,2008,22(4):1-6. DOU Peilin, WANG Huihui. Strength analysis of jacket platform[J].Journal of Jiangsu University of Science and Technology: Natural Science Edition,2008,22(4):1-6.
[6] 郑忠双.结构随机响应分析及其动力可靠性研究现状及趋势[J].福建建筑,2002(1):25-28. ZHEGN Zhongshuang. Current situation and trend of structural random response analysis and dynamic reliability analysis of[J].Fujian Building,2002(1):25-28.
[7] PARK M, KOO W, KAWANO K. Dynamic response analysis of an offshore platform due to seismic motions[J].Engineering Structures,2011,33(5):1607-1616.
[8] ZHUANG Y, JIN W. Aseismic reliability analysis approach for offshore jacket platform structures[J].China Ocean Engineering,1998,4(4):375-382.
[9] 赵洲,张火明.60万桶FPSO船体在十年一遇海况下的大幅运动模拟[J].中国计量学院学报,2012,23(4):410-414. ZHAO zhou, ZHANG Huoming. Simulation of large movements of 600000 barrels of FPSO hull in ten years under the condition[J].Journal of China University of Metrology,2012,23(4):410-414.
[10] 李宁.随机波浪载荷下海洋平台的振动控制技术研究[D].青岛:中国海洋大学,2012. LI Ning. Vibration control of offshore platform under random wave loads[D].Qingdao: Ocean University of China,2012.
[11] 余建星,陈煜嘉,陈飞宇,等.在役导管架平台动态可靠性研究[J].船舶工程,2015,37(8):98-102. YU Jianxing, CHEN Yujia, CHEN Feiyu, et al. Study on the dynamic reliability of the service jacket platform[J].Ship Engineering,2015,37(8):98-102.
[12] 魏晓添.海洋导管架结构的现状研究及应用前景[J].山西建筑,2010,36(19):102-103. WEI Xiaotian. The present situation of the structure of the offshore jacket and its application prospect[J].Shanxi Architecture,2010,36(19):102-103.
Analysis of vibration response of jacket platform
XIE Zhuo1, ZHANG Huoming1, Fang Guisheng2, XU Ling1
(1. College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China; 2. College of Mechanical and Automotive Engineering, Zhejiang Water Conservancy and Hydropower College, Hangzhou 310018, China)
The dynamic characteristic of marine structures is of importantance to the fatigue life estimation. We established a simple model to analyze the frequency response of the platform under random wave excitation. The load and the vibration displacement response of the double deck jacket platform were derived by using the Morrison equation under the inertial system. The Pierson-Moskowitz (P-M) spectra of wave heights of 15 m, 20 m, 25 m were obtained. The results showed that, under the same frequency, the wave height had greater impact on the response of the jacket platform. We also discussed the variance of the displacement and the extreme value of the response of the vibration displacement.
jacket platform; random wave; vibration response
1004-1540(2015)04-0423-05
10.3969/j.issn.1004-1540.2015.04.007
2015-07-10 《中国计量学院学报》网址:zgjl.cbpt.cnki.net
国家自然科学基金资助项目(No.51379198),浙江省自然科学基金资助项目(No.Y14E090034,Y13F020140),浙江省青年科学家培养计划项目(No.2013R60G7160040).

TG703;O342
A

