Gabor滤波器的掌纹特征提取研究

梅支礼,陶海军,王加强

(1.中国计量学院 信息工程学院,浙江 杭州 310018;2.北京市新技术应用研究所,北京 100094)

Gabor滤波器的掌纹特征提取研究

梅支礼1,陶海军1,王加强2

(1.中国计量学院 信息工程学院,浙江 杭州 310018;2.北京市新技术应用研究所,北京 100094)

掌纹识别是近年发展起来的一种生物识别技术,掌纹特征提取是掌纹识别核心部分之一,传统Gabor滤波器特征提取速度慢致使掌纹识别速度不能满足实时性的要求.将传统Gabor、改进Gabor和迭代Gabor应用于掌纹特征提取,对比研究了它们在掌纹识别中特征提取速度和识别精度的问题,旨在探求识别精度高且特征提取速度更快的Gabor滤波器,进而改良掌纹特征提取方法.实验表明,迭代Gabor滤波器能确保掌纹识别系统在高识别精度的前提下具有更快的识别速度.

掌纹识别;特征提取;迭代Gabor

生物识别[1](Biometrics Recognition)是指利用人体固有的生理特征如人脸、虹膜、指纹等和行为特征如手姿、签名、声音等实现身份鉴别的一种技术.它具有可靠性高、稳定性强、安全快捷等特点.随着信息安全重要性的持续增强,生物特征识别技术凭借其在身份认证方面的卓越优势,越来越为人们所关注,并已广泛应用于安全保密、认证防伪、考勤打卡和刑事侦破等领域.

掌纹识别[2]是近些年新发展起来的一种生物特征识别技术,相比其他传统生物识别技术掌纹识别还有许多亟待研究解决的问题.掌纹识别主要是指利用人手掌掌纹主线、褶皱和乳突纹等特征信息实现个人身份认证.掌纹识别不仅包含传统生物识别的优点,还具有特征信息丰富稳定、用户接受度高、受外界条件影响较小、采集设备价格低等特点.特征提取是掌纹识别的核心部分,掌纹特征提取决定了掌纹识别系统的识别速度和精度,因此本文研究掌纹特征提取方法具有非常重要的现实意义.

Gabor滤波器能较准确模拟哺乳动物视觉皮层简单细胞的二维感受野并具有方向选择性,能反映图像纹线特征[3].文献[4]指出Gabor滤波器具有良好滤波特性:1)Gabor滤波器具有不同的空间频率带宽、空间尺度和方向,可以实现空域和频域的最优化;2)Gabor滤波器能得到对于失真具备一定鲁棒性的特征空间,且对图像对比度及亮度变化具有很好的鲁棒性.因此,Gabor滤波器非常适合皮肤类纹理的特征提取.文献[5]将Gabor滤波器应用于人脸识别的特征提取;文献[6]将Gabor滤波器应用于指纹识别的特征提取;文献[7]将Gabor滤波器应用于虹膜识别的特征提取.Gabor滤波器已广泛应用于皮肤纹理类生物特征识别并达到了较理想的识别精度;然而,识别速度并不能很好地满足当今应用需求,传统Gabor滤波器特征提取速度还有待提高,现实应用迫切需要特征提取速度更快的Gabor滤波器.

文献[8]提取出了Gabor滤波器的一般形式,记其为传统Gabor;文献[9]中LEE结合神经生理学改进了Gabor滤波器,记其为改进Gabor;本文论述迭代方式实现的Gabor滤波器,记其为迭代Gabor.实验将传统Gabor、改进Gabor和迭代Gabor应用于掌纹识别,对其在掌纹识别中特征提取速度和识别精度两个方面进行对比研究.

1 Gabor滤波器

1946年,Dennis Gabor为解决傅里叶变换不能提取局部信息的缺点而提出了短时傅里叶变换(STFT),后人称之为Gabor变换[10].Gabor变换的实质是一种加了高斯窗的Fourier变换,可以认为Gabor变换是短时Fourier变换中当窗函数为高斯函数的一种特殊情况.在此基础上,1985年Daugman在文献[11]中提出2D Gabor滤波器,图1是2D Gabor滤波器和哺乳动物视觉皮层简单细胞二维感受野的比较.

图1 2D Gabor滤波器和哺乳动物视觉皮层简单细胞二维感受野的比较Figure 1 Comparison of 2D Gabor filter and the two dimensional feeling wild of simple cell of mammalian visual cortex

本文Gabor滤波器是用于掌纹图像滤波,因此用于滤波的滤波器均为2D Gabor滤波器.2D Gabor滤波器具方向选择性,当掌纹方向与滤波器方向一致或相近时,滤波器响应较大.此时用滤波器方向代替掌纹方向,记录滤波器方向就能有效提取掌纹纹线方向信息.据神经生理的研究发现,简单细胞对带宽为π/6倍数的特殊角度敏感,因此本文中选择的角度信息为θ={0°,30°,60°,90°,120°,150°}的一组2D Gabor滤波器进行滤波.滤波器组如图2.

图2 2D Gabor滤波器组Figure 2 2D Gabor filters

2D Gabor滤波器广泛应用于皮肤纹理特征提取.针对具体应用的要求,学者们对Gabor滤波函数和Gabor滤波函数的实现方式作出了相应的变换,常见的2D Gabor滤波器有以下几种形式.

1.1 传统Gabor

传统Gabor滤波器可理解为高斯基函数与复正弦波函数的乘积,是一种线性滤波器,其构建方式可描述为如式(1):

(1)

其中:λ和θ—正弦波波长和方向;x′=xcosθ+ysinθ,y′=-xsinθ+ycosθ;σx和σy—高斯包络在x方向和y方向上的标准差.

1.2 改进Gabor

改进Gabor滤波器是由LEE基于哺乳类动物大脑视觉皮层神经生理迹象和小波理论改进而成,其函数如式(2):

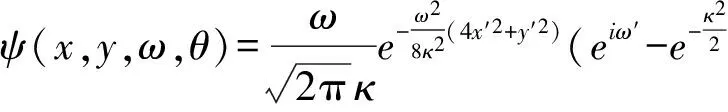
(2)

1.3 迭代Gabor

由式(1)知，2D Gabor函数是由2D Gaussian函数经复正弦函数调制而来.又由Z空间性质可知:高斯函数乘以一个调制因子意味着在Z平面中围绕中心z(0,0)旋转了一定角度.若能实现迭代2D Gaussian,则可由迭代2D Gaussian推导迭代2D Gabor.文献[12]将2D Gaussian函数在时域分解为2个非正交的1D高斯函数,文献[13]指出1D高斯函数可通过1次前向迭代和1次后向迭代进行逼近.因此迭代2D Gaussian可由2次迭代1D Gaussian即2次前向迭代和2次后向迭代实现,类似的迭代2D Gabor可由2次迭代1D Gabor实现.下面为迭代1D Gabor的实现过程.

1D高斯函数可描述为

(3)

1D Gabor函数可描述为

(4)

对式(3)进行傅里叶变换可得

G(ω)=F(g(t,σ))=e-σ2ω2/2.

(5)

文献[13]中还实现了对高斯函数的有理逼近,如式(6):

(6)

其中，a0=2.490 895,a2=1.466 003,a4=0.024 393,a6=0.178 257.将式(6)理解为对高斯函数的傅里叶变换的逼近,那么式(5)的傅里叶变换可以表述为式(7):

(7)

用q代替σ,用s代替ω，式(7)由傅里叶变换域转换为s域,记为式(8):

(8)

(9)

由式(6)中系数可求得:m0=1.166 8,m1=1.107 83,m2=1.405 86.将(9)由s域变换到Z域得式(10):

(10)

其中b0、b1、b2、b3及B值的求解参见文献[14].

式(10)由两部分组成,第一部分可类比为迭代1D Gaussian中的前向迭代,第二部分可以类比为迭代1D Gaussian中的后向迭代.由Z空间性质Gabor变换可由式(10)推导得到,记为式(11):

(11)

其中b0、b1、b2及b3值的求解参见文献[15].

通过此方法实现了迭代1D Gabor,类似2D Gaussian非正交分解的方法将2D Gabor分解为两个非正交的1D Gabor,用迭代的方式分别实现这两个1D Gabor,则可实现迭代2D Gabor.由Gabor滤波函数和Gabor滤波函数的实现方式可知,Gabor滤波特性受σ影响较大.

2 实验结果分析

实验基于北京市新技术应用研究所的掌纹样本库,包含149个不同掌纹,每个掌纹取30幅图像,共计4470幅图像.实验在Intel(R)Core(TM)i5-3470@3.20 GHz,64位Win7操作系统及MATLAB 2010a上进行.在实验中传统Gabor和改进Gabor对手掌图像特征提取均采用卷积滤波的方法,迭代Gabor则是采用迭代的方法.实验对滤波器组滤波六个结果中响应最大者用竞争编码[16]的方法对其进行编码,对编码的结果按位计算汉明距离比较判别进而完成匹配识别.由于Gabor函数的性质主要受σ影响,卷积滤波则与滤波函数模板大小相关,即Gabor函数的σ和滤波函数模板大小是影响掌纹特征提取速度和识别精度的两个主要因素.因此，在对比研究特征提取速度和掌纹识别精度时,实验采用确定一个影响因素改变一个影响因素的方案进行.

2.1 特征提取速度比较

特征提取速度主要用滤波器对掌纹图像完成特征提取时耗进行评价.实验分别记录了传统Gabor、改进Gabor和迭代Gabor对1000幅掌纹图像进行特征提取的总时耗.当Gabor函数的σ不变(实验中取σx=7.5,σy=3)时,改变滤波函数模板大小,滤波器对1000幅掌纹图像特征提取总时耗如表1.

表1 滤波函数模板大小不变改变σ特征提取时耗

Table 1 Time of feature extraction needed when theσchanges while the size of the template of the filter functions is invariant

s

注:由于迭代Gabor滤波和模板大小无关,因此3组实验迭代Gabor时耗一致.

当滤波函数模板大小不变(实验中取19×19),改变Gabor函数的σ,滤波器对1 000幅掌纹图像特征提取的总时耗如表2.

表2 滤波函数模板大小不改变改变σ特征提取时耗

Table 2 Time of feature extraction needed when the size of the template of the filter functions changes while theσis invariant

s

当σ不变改变滤波函数模板大小时,由表1可知:1)迭代Gabor的特征提取速度远快于传统Gabor和改进Gabor,改进Gabor略快于传统Gabor;2)传统Gabor和改进Gabor随着滤波函数模板的增大特征提取时耗增加,迭代Gabor特征提取时耗与滤波函数模板大小无关.

当滤波函数模板大小不变改变σ时,由表2可知:1)迭代Gabor的特征提取速度远快于传统Gabor和改进Gabor,改进Gabor略快于传统Gabor;2)σ对特征提取速度影响较小,对于相同特征提取方法而言,当σ变化时,不同尺寸的σ滤波速度变化较小.

综上可知:1)特征提取速度迭代Gabor远快于传统Gabor和改进Gabor;2)迭代Gabor特征提取速度与滤波函数模板大小无关,传统Gabor和改进Gabor特征提取速度与滤波函数模板大小成正比关系;3)σ对特征提取速度影响较小.

2.2 掌纹识别精度

掌纹识别精度主要由正确接受率(genuine acceptance rate, GAR)和错误识别率(false acceptance rate, FAR)来衡量.正确接受率是指识别系统准确地把来自同一人的掌纹判定为来自同一人的概率;错误识别率是指识别系统错误地把来自不同人的掌纹判定是来自同一个人的概率.显然当特征提取算法的GAR越高时,算法具有越高的特征提取精度.实验中,每幅掌纹图像和来自同一手掌的另外29幅掌纹图像以及来自不同手掌的掌纹图像进行匹配,为提高匹配效率在和来自不同手掌掌纹图像匹配时每个手掌取2幅图像进行.因此实验进行了64 786次相同手掌掌纹间的匹配及652 402次不同手掌掌纹间的匹配.ROC曲线[17]是最常用的评价生物识别性能的手段之一,实验用GAR与FAR关系的ROC曲线对比研究传统Gabor、改进Gabor和迭代Gabor的掌纹识别精度.

当Gabor函数的σ不变(实验中取σx=7.5,σy=3)改变滤波函数模板大小(模板大小分别取:13×13,19×19,25×25)时,传统Gabor、改进Gabor和迭代Gabor的GAR与FAR关系的ROC曲线如图3.

图3 滤波函数σx=7.5,σy=3改变滤波函数模板大小时，传统Gabor、改进Gabor和迭代Gabor的GAR与FAR关系的ROC曲线Figure 3 ROC relationship of the GAR and FAR of the traditional Gabor, improved Gabor and recusive Gabor when the σx=7.5,σy=3

当滤波函数模板大小不变(实验中取19×19),改变σ(实验中(σx,σy)分别取(8,2),(7.5,3),(10,4))时,传统Gabor、改进Gabor和迭代Gabor的GAR与FAR关系的ROC曲线如图4.

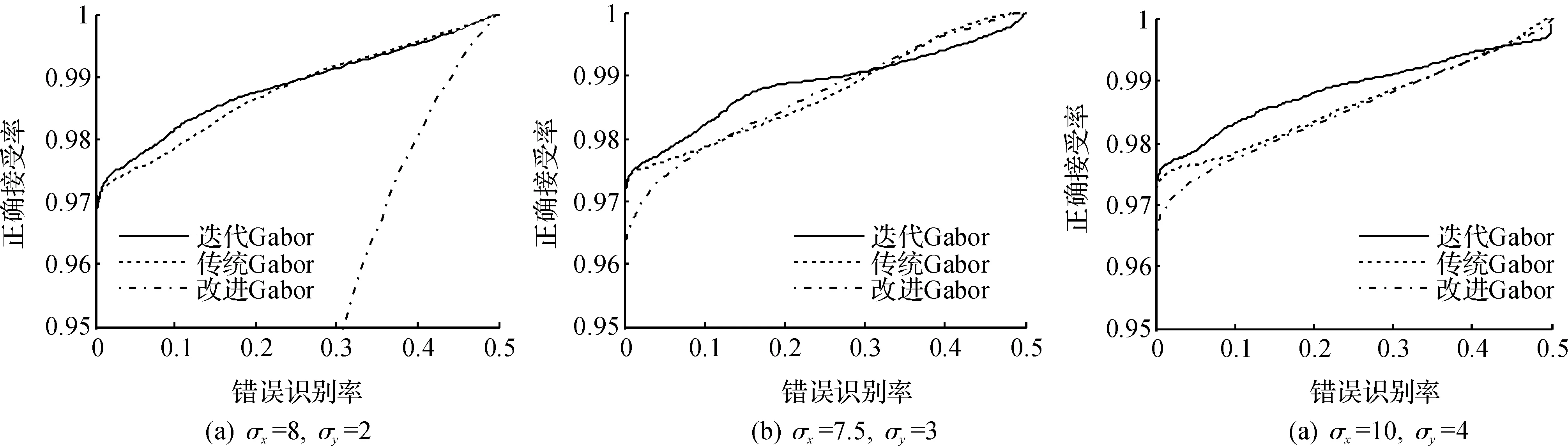
图4 滤波函数模板大小为19×19改变σ时,传统Gabor、改进Gabor和迭代Gabor的GAR与FAR关系的ROC曲线Figure 4 ROC relationship of the GAR and FAR of the traditional Gabor, improved Gabor and recusive Gabor when the template of the filter functions is 19×19

当σ不变改变滤波函数模板大小时,由图3可知,掌纹识别精度受模板大小影响较小,传统Gabor、改进Gabor和迭代Gabor的掌纹识别精度都较高.当FAR较小时,迭代Gabor具有最高GAR,这是现实应用所希望的.当滤波函数模板大小不变改变σ时,由图4可知,迭代Gabor具有更好的识别精度,选择合适的σ对掌纹识别精度具有较大影响.

综上可知:(1)选择合适的σ时,传统Gabor、改进Gabor和迭代Gabor都具有较高的识别精度,迭代Gabor识别精度更符合现实应用的要求.文献[14]指出迭代高斯每个像素的计算与前面三个像素和后面三个像素密切相关,即迭代高斯能很好地反映图像像素间的联系,能更好地提取图像特征.迭代Gabor由迭代高斯推导而来,故迭代Gabor能很好地提取掌纹图像的特征以保证迭代Gabor具有满意的识别精度.(2)滤波函数模板大小对识别精度影响较小,σ对识别精度影响较大.

3 结 语

本实验实现了传统Gabor、迭代Gabor和改进Gabor应用于掌纹识别.为不失一般性实验中选取了多种σ值和滤波函数模板大小.实验表明较之传统Gabor和改进Gabor,迭代Gabor在掌纹识别中确保了高识别精度的前提下具有更快的特征提取速度.即基于迭代Gabor的掌纹识别系统在确保高识别精度的前提下具有更快的识别速度更能满足现实应用的需求.

2012年四位来自麻省理工的研究人员提出了一种运算速度比快速傅里叶变换快10倍至100倍的新算法——稀疏傅里叶变换(SFT).掌纹信息在掌纹图像中也属于稀疏信息,原理上讲SFT可应用于掌纹特征提取.实际应用常用的一种策略是用离散Gabor近似以加快计算速度,因此后续的工作将探讨SFT应用于掌纹特征提取并与离散Gabor进行对比研究.

[1] CHEN Fanglin, HUANG Xiaolin, ZHOU Jie. Hierarchical minutiae matching for fingerprint and palmprint identification[J].IEEE Transactions on Image Processing,2013,22(12):4964-4971.

[2] LIU Zhonghua, PU Jiexin, HUANG Tao, et al. A novel classification method for palmprint recognition based on reconstruction error and normalized distance[J].Applied Intelligence,2013,39(2):307-314.

[3] WANG Xuan, LEI Li, WANG Mingzhe. Palmprint verific- ation based on 2D Gabor wavelet and pulse coupled neural network[J].Knowledge Based Systems,2012,27:451-455.

[4] LEE J C, LEE C H, HSU C B, et al. Dorsal hand vein recognition based on 2D Gabor filters[J].Imaging Science Journal,2014,62(3):127-138.

[5] WANG Ning, LI Qiong, ABD E A, et al. An enhanced thermal face recognition method based on multiscale complex fusion for Gabor coefficients[J].Multimedia Tools and Applications,2014,72(3):2339-2358.

[6] KHAN T M, KHAN M A U, KONG Yinan. Fingerprint image enhancement using multiscale DDFB based diffusion filters and modified Hong filters[J].Optik,2014,125(16):4206-4214.

[7] RADMAN A, JUMARI, ZAINAL N. Fast and reliable iris segmentation algorithm[J].IET Image Processing,2013,7(1):42-49.

[8] ZHANG Weichuan, WANG Fuping, ZHU Lei, et al. Corner detection using Gabor filters[J].IET Image Processing,2014,8(11):639-646.

[9] LEE T S. Mage represention using 2D Gabor wavelet[J].IEEE Trans Image Processing,1996,18(10):959-971.

[10] DENNIS G. Theory of communication[J].IEEE Trans Image Processing,1946,93(3):429-457.

[11] DAUGMAN J G. Uncertainty relation for resolution in space, spatial frequency and orientation optimized by twodimensional visual cortical filters[J].Optics and Image Science,1985,2(7):1160-1169.

[12] GEUSEBROKE J M, SMEULDERS A W M, WEIJER J. Fast anisotropic gauss filtering[J].IEEE Trans Image Processing,2003,12(8):938-943.

[13] VAN V L, YOUNG I T, VERBEEK P W. Recursive Gaussian derivative filters[C]//Proceedings of Fourteenth International Conference on Pattern Recognition. Risbane: IEEE Computer Society Press,1998:509-514.

[14] YOUNG I T, AN V L. Ecursive implementation of the Gaussian filter[J].Signal Processing,1995,44: 139-151.

[15] WOLFRAM S. A system for doing mathematics by computer[M].2nd ed. Addison Wesley: Books/ Mathematic,1991:432-460.

[16] GAO Guangwei, YANG Jian, QIAN Jianjun, et al. Integration of multiple orientation and texture information for finger-knuckle-print verification[J].Neurocomputing,2014,135:180-191.

[17] GU Jiezhun, GHOSAL S, KLEINER D E. Bayesian ROC curve estimation under verification bias[J].Statistics in Medicine,2014,33(29):5081-5096.

Study of Gabor filters on palmprint feature extraction

MEI Zhili1, TAO Haijun1, WANG Jiaqiang2

(1. College of Information Engineering, China Jiliang University, Hangzhou 310018, China;2 .Beijing Institute of New Technology Applications, Beijing 100094, China)

Palmprint recognition is a kind of biological recognition technology developed in recent years.Palmprint feature extraction is the core of palmprint recognition.Traditional Gabor filters can not meet the requirement of the real-time palmprint recognition system because of the slow speed of featue extraction. A traditional Gabor, am improved Gabor and a recursive Gabor were used in the palmprint feature extraction in this paper.We studied their speed of feature extraction and the recognition accuracy of palmprint recognition comparatively to find a filter with high recognition accuracy and faster feature extraction speed.The experiments show that the recursive Gabor has the fastest feature extraction speed in the premise of ensuring palmprint recognition accuracy under high recognition accuracy.

palmprint recognition; feature extraction; recusive Gabor

1004-1540(2015)03-0347-06

10.3969/j.issn.1004-1540.2015.03.018

2015-05-15 《中国计量学院学报》网址：zgjl.cbpt.cnki.net

北京市科技计划项目(No.Z131100004113001).

梅支礼(1987- )，男，湖北省黄冈人，硕士研究生，主要研究方向为模式识别、图像处理.E-mail：cjlumike@163.com 通讯联系人：陶海军，男，副教授．E-mail：hjtao@cjlu.edu.cn

TP391.41

A