采用多站接力跟踪策略的再入返回器定轨精度研究

段建锋谢剑锋张宇陈明段成林王震宇

（1北京航天飞行控制中心，北京 100094）

（2航天飞行动力学技术重点实验室，北京 100094）

采用多站接力跟踪策略的再入返回器定轨精度研究

段建锋1，2谢剑锋1，2张宇1，2陈明1，2段成林1，2王震宇1

（1北京航天飞行控制中心，北京 100094）

（2航天飞行动力学技术重点实验室，北京 100094）

针对我国探月工程再入返回段分离前的精度要求，在无法实现对再入返回器的三向测量情况下，提出多站接力跟踪的测量策略，以解决测定轨精度不高的问题。结合再入返回分离前的测控弧段，制定两站及三站接力跟踪的策略。利用ESA“桑巴”（SAMBA）卫星进行多站接力跟踪试验数据分析，结果表明，三站接力跟踪策略的定轨预报精度优于两站接力跟踪策略，能够实现返回器安全可靠地再入返回，可为再入返回任务分离前跟踪策略的制定提供依据。

再入返回器；多站接力跟踪；“桑巴”卫星；定轨试验；精度分析

1 引言

根据我国探月工程“绕、落、回”分步实施的原则［1］，嫦娥一号和嫦娥二号的成功标志着第一步圆满完成［2-3］，嫦娥三号任务的成功标志着第二步圆满完成［4］。目前，探月工程已转入第三步，主要目标是实现月面采样返回，包括“再入返回飞行试验”（Chang'e-5T1）、嫦娥五号（Chang'e-5）和嫦娥六号（Chang'e-6）3次任务。其中，“再入返回飞行试验”任务主要用于验证与半弹道跳跃式再入返回相关的技术，确保嫦娥五号等后续再入返回器技术方案的可行性和正确性，为嫦娥五号任务的顺利实施奠定基础。“再入返回飞行试验”任务中的返回器自月球返回直接再入地球大气，速度约为11 km/s，再入角约为―6°，着陆场位于43°N附近地区。受地月空间几何限制，再入点位于赤道附近的低纬度地区，再入航程在6000 km以上［5］，再入速度远高于约7.8 km/s的近地轨道再入速度［6］。为确保此类再入返回器可以成功返回地面，要在分离点3 h前进行轨道确定，并预报至分离点（即返回器脱离主航天器开始返回地球的时刻），提高分离点定轨预报精度，以保证返回器精确返回着陆场所需注入的再入角的精度要求。

根据我国着陆场的地域特点及再入返回器轨道设计特点，我国再入返回器分离前的轨迹一般在南半球的圣地亚哥站及纳米比亚站的测控范围内，因为返回器本身下行频段的局限性，而且在嫦娥三号任务中，我国成功使用了三向测量技术并获得较高的测量精度及轨道确定精度［7］，因此最理想的状态是寻找一个位于北半球的测站，与我国南半球的两站建立三向测量体制。由文献［7］中对我国深空站三向测量模式的数据精度分析，以及文献［8］中对我国深空任务的三向测量数据分析可知，三向测量体制下的数据精度要明显优于双向相干测距测速体制，可以满足分离点定轨预报精度要求。不过，目前无法找到与圣地亚哥站、纳米比亚站测量机制相同的测站，因此无法建立起三向测量模式。为保障探测器在分离点的定轨预报精度，确保返回舱的顺利返回，本文提出多站接力跟踪的测量方式。

多站接力跟踪是指针对探测器在多个测站的观测弧段内但无法实现多测站同时跟踪的问题，为改进观测数据的定轨几何约束，采用多个测站、不同时间的数据（测距、测速、测角）进行轨道测量、轨道确定的方法。国外在进行此类再入返回飞行时不存在相关测控的局限性，因此这一测控模式在国外的飞行任务中使用较少。在国内，对该模式的研究也处于起步阶段。多站接力跟踪测控策略相对于三向测量，存在着测控弧段不连续、测量数据少、观测几何约束弱化等诸多问题，因此接力跟踪策略的制定对定轨精度的改善显得尤为重要，要考虑参加联合接力跟踪的测站跟踪顺序和时间分配等问题。为获取最优的接力跟踪策略，确保该策略下的测定轨精度稳定可靠，本文研究了使用两站、三站的接力方法，给出轨道测量策略、预报方法和精度的估计。假设三站参加测控的条件下，采用双站接力及三站接力进行测控的方法，探究接力测量测站的个数、几何约束对轨道确定的影响。结合ESA“桑巴”（SAMBA）卫星试验数据分别进行精度估计，可获得以下结论：三站接力跟踪策略定轨精度最高；不同两站组合，由于站的位置和设备精度的差异，获得不同的精度，但精度均不高。

2 多站接力跟踪策略

三向测量是指利用主站发射上行信号，经探测器应答机相干转发后，由另一测站（副站）进行信号接收的测量体制。如图1（a）所示，三向测量通常由3个地面测站配合完成测量，获得测站到探测器的距离。多站接力跟踪策略如图1（b）所示，是指按照约定的观测顺序及时间分配，各测站独立完成数据收发的测量模式。在各测站均共视的情况下，三向测量体制的定轨精度优于接力跟踪测量策略。

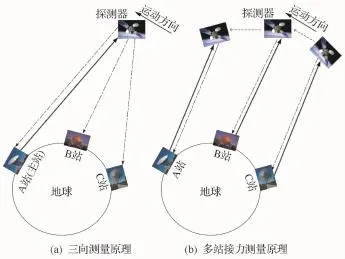
图1 测量模式原理Fig.1 Principle of measurement mode

根据我国着陆场的设置，返回器着陆前经过的星下点区域一般在南美洲、大西洋、非洲，目前我国有圣地亚哥、纳米比亚两站。对于高速再入返回的月球探测器而言，在无法实现三向测量的情况下，则要验证两站的测量定轨精度是否可以达到任务要求。基于可实现的前提下，本文结合我国再入返回器分离前的测控弧段，制定了双站接力跟踪及三站接力跟踪两种策略的跟踪策略。其中，第三站假设为ESA的玛斯帕拉玛斯站。

具体而言，三站接力跟踪策略是指使用纳米比亚站、圣地亚哥站、玛斯帕拉玛斯站的跟踪测量数据进行定轨分析，组合其中两站的跟踪测量数据进行定轨精度分析，为双站接力跟踪策略。再入返回器经过此测控区至再入分离前的时间约为3 h，本文在考虑站间切换时间及其他因素的影响后，制定如表1所示的接力跟踪计算策略。因为玛斯帕拉玛斯站在北半球，为优化三角几何关系，因此在时间分配上多于其他两站。

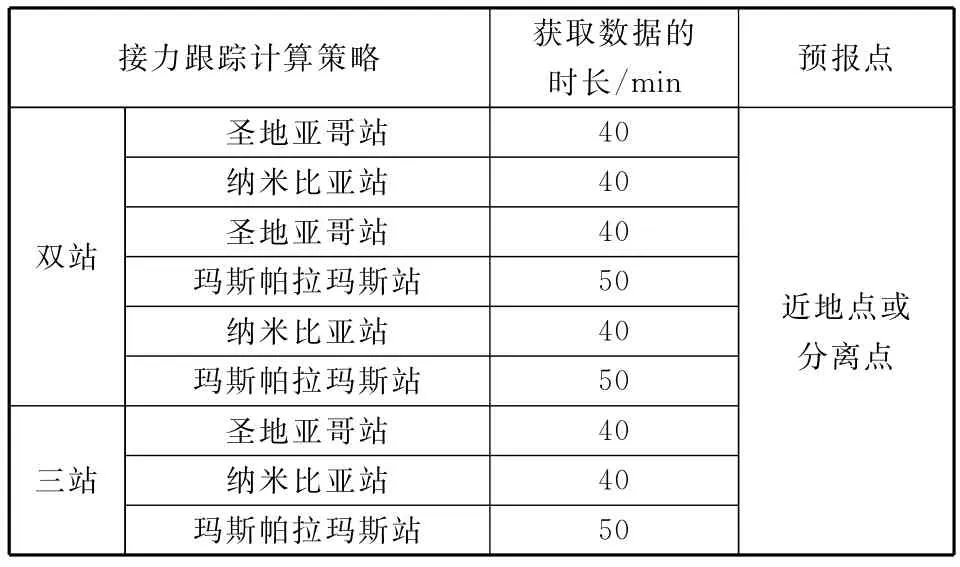
表1 多站接力跟踪计算策略Table 1 Analytic strategies of multiple station relay tracking

3 测轨方法试验

3.1 试验概述

经过对现有的大椭圆卫星进行梳理可知，ESA的“星团”（Cluster）计划［9］卫星在过近地点时与我国再入返回器的轨道特性及测控弧段相似。“星团”计划包括“萨尔萨”（SALSA）、“桑巴”（SAMBA）、“伦巴”（RUMBA）、“探戈”（TANGO）4颗卫星，均于2000年发射升空，构成地球空间星座探测计划。根据卫星测控条件等约束，在与ESA协商后，确定利用SAMBA卫星过近地点时的弧段进行测定轨试验。

SAMBA卫星近地点高度约为1.7万千米，远地点高度约为11.58万千米，轨道倾角约为134°，偏心率约为0.68。选取SAMBA卫星飞过近地点时的测控弧段时间为2014年4月24日（UTC时间，下同）。在试验测量弧段内，测站测量设备须提供每秒一点的S频段测距、测速和测角数据［10］，测站每分钟提供一次气象数据。其中，测量设备零值和设备轴系误差均由设备级计算机修正，电波修正利用气象数据修正。试验具体测量弧段安排见图2。

根据试验安排，参试测站纳米比亚站、圣地亚哥站及玛斯帕拉玛斯站获取的数据，实际测量弧段如表2所示。为了确保测轨数据质量，对本次试验的外测数据进行数据合理性检验、星上零值修正、大气折射修正等处理［11］。

图2 测量弧段安排Fig.2 Arrangements of measurement arcs

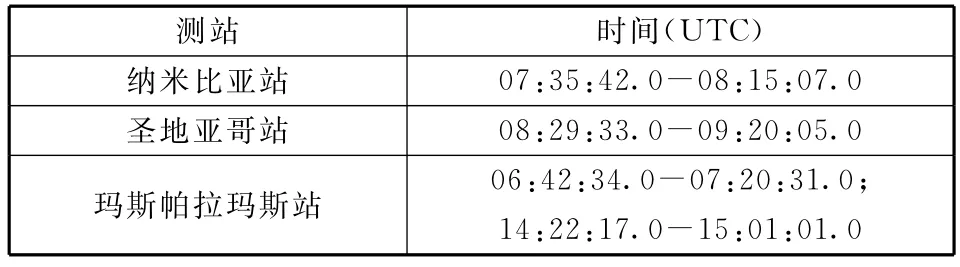
表2 实际测量数据弧段（2014年4月24日）Table 2 Actual measurement arcs（2014-04-24）

根据所得数据分别进行双站（圣地亚哥站和纳米比亚站，圣地亚哥站和玛斯帕拉玛斯站，纳米比亚站和玛斯帕拉玛斯站）接力定轨预报分析，以及三站（圣地亚哥站、纳米比亚站、玛斯帕拉玛斯站）接力定轨预报分析，预报终点选在SAMBA卫星过近地点的时间点11：20：00.000（UTC）。通过比较得出最优精度的接力跟踪计算策略。

3.2 试验精度分析

3.2.1 基准星历计算

本次试验可以获得2条基准轨道，其中一条是ESA提供的SAMBA卫星在试验弧段的精密星历，称为基准星历1；另一条是本文利用玛斯帕拉玛斯站、纳米比亚站、圣地亚哥站在SAMBA卫星过近地点前后所有参试的有效测量数据进行定轨得到的，称为基准星历2，具体的弧段为2014-04-24 T06：42：00.000―15：00：00.000（UTC），这些数据包含了SAMBA卫星飞越近地点前后（如图2所示）的多段测量数据。轨道计算分析采用北京航天飞行控制中心的“轨道计算与分析软件平台”（BACC Orbit Determination and Analysis System，BODAS）［12］，定轨基本策略［13］如表3所示。因在数据处理中已扣减过星上零值，在以下定轨过程中未对测量数据解算系统差。定轨数据残差见表4所示。

基准星历1与基准星历2在轨道面径向（R）、横向（T）及法向（N）3个方向的比较结果，如图3及表5所示。其中，ΔrR，ΔrT，ΔrN和ΔνR，ΔνT，ΔνN分别表示R，T，N方向的位置误差和速度误差。结果显示，2个基准星历位置误差在百米量级，速度误差在厘米每秒量级，处于可信区间。

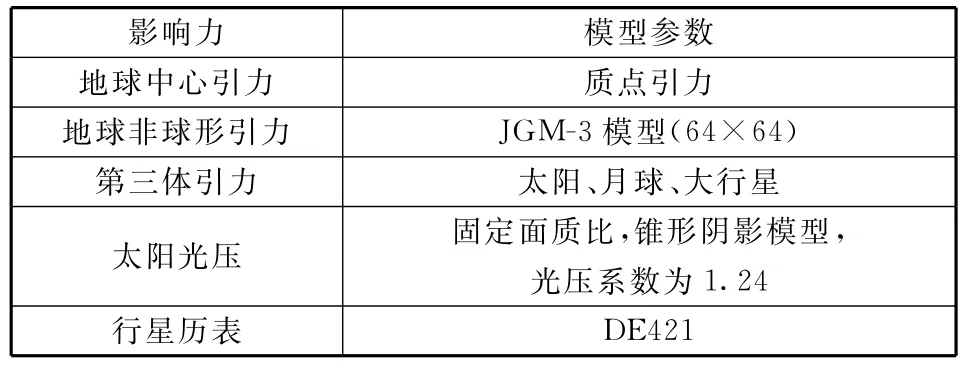
表3 定轨基本策略Table 3 Basic orbit determination strategy

表4 定轨数据残差统计Table 4 Statistics of orbit determination data RMS

表5 基准星历的互比结果Table 5 Comparative results of two reference ephemeris

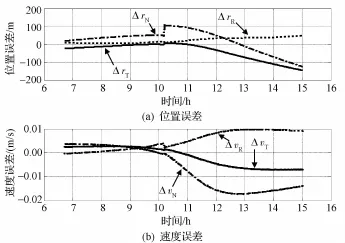
图3 2个基准星历R，T，N方向位置和速度误差Fig.3 Position and velocity error on R，T and N comparison between two reference ephemeris

3.2.2 定轨精度比较分析

3.2.2.1 双站接力策略

为了探究双站接力的可能性，根据表1，在试验中采用3种双站接力策略：①纳米比亚站与圣地亚哥站的接力策略；②纳米比亚站与玛斯帕拉玛斯站的接力策略；③圣地亚哥站与玛斯帕拉玛斯站的接力策略。利用表2所示相关弧段进行定轨预报分析，纳米比亚站、圣地亚哥站、玛斯帕拉玛斯站的测距数据定轨残差分别为3.0 m、3.0 m、1.4 m，测速数据定轨残差（未解系统差）分别为4 cm/s、3 cm/s、7 cm/s。

将获取的定轨预报星历分别与基准星历1和基准星历2进行比较，得到R，T，N方向的比较结果，见表6。可以看出，纳米比亚站与玛斯帕拉玛斯站的接力策略效果最好，圣地亚哥站与玛斯帕拉玛斯站的最差，纳米比亚站与圣地亚哥站的居中。这是因为圣地亚哥站与玛斯帕拉玛斯站接力策略在本次试验中没有实现真正的接力，影响了定轨及预报精度；纳米比亚站与圣地亚哥站接力策略中，测站全在南半球，影响了测量数据的观测几何，无法更好地约束大椭圆类型轨道；纳米比亚站与玛斯帕拉玛斯站接力策略中，在南北半球各有一个测站，而且跟踪测量数据相对连续，弥补了前两种策略的缺点，在既能约束SAMBA卫星的观测几何，又能连续测量的情况下，获得了较好的定轨预报精度。纳米比亚站与玛斯帕拉玛斯站接力策略下与2个基准星历比较，位置定轨预报误差均在千米量级或者接近千米量级，速度定轨预报误差均在分米每秒量级。

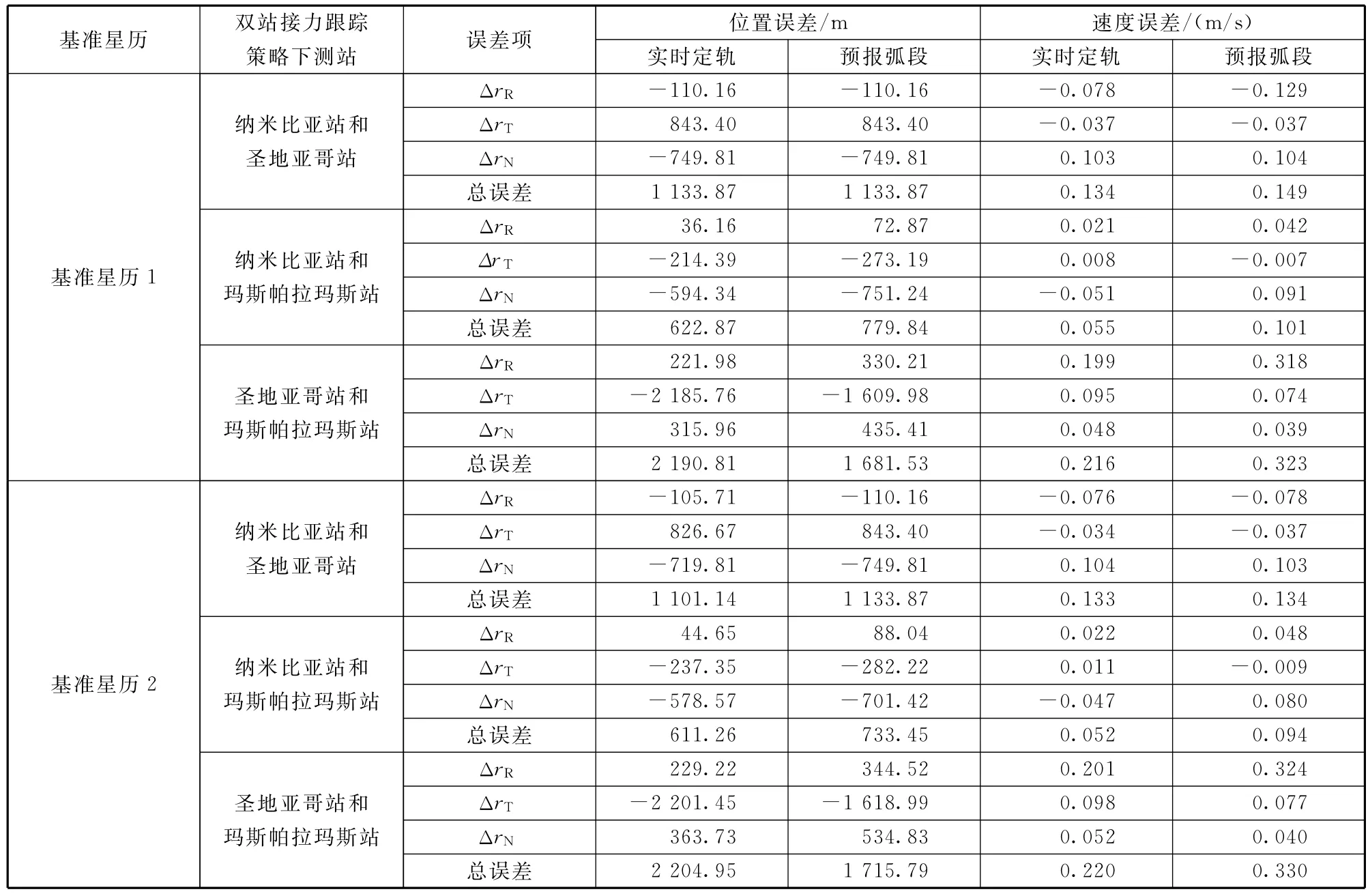
表6 双站接力跟踪策略星历与基准星历的比较结果Table 6 Comparison results between reference ephemeris and double station relay tracking strategy's ephemeris

3.2.2.2 三站接力策略

根据表1，三站接力策略指利用纳米比亚站、圣地亚哥站、玛斯帕拉玛斯站进行接力测量的测控方式。数据的使用方式及残差解算结果与双站接力策略一致。将获取的定轨预报星历分别与基准星历1和基准星历2进行比较，获取R，T，N方向的比较结果，见表7。对比双站接力策略，三站接力策略既能解决观测数据量及观测数据连续性问题，又能兼顾测站对观测几何的影响。

由表7可知，在三站接力策略下，位置定轨预报误差均在百米量级或者优于百米量级，速度定轨预报误差均在厘米每秒量级。比对表6结果，三站接力策略的定轨预报精度优于双站接力策略一个量级以上。

根据上述分析结果，三站接力跟踪策略精度最优，可以满足在近地点的定轨精度要求，这一策略在再入返回任务中可以借鉴采用。

表7 三站接力跟踪策略星历与基准星历的比较结果Table 7 Comparison results between reference ephemeris and three station relay tracking strategy's ephemeris

4 结束语

本文针对我国探月工程再入返回器返回分离前的特殊测控需求及精度要求，提出了多站接力跟踪策略，制定了多站接力跟踪策略，并结合ESA的SAMBA卫星定轨试验数据进行了分析。对比多站接力跟踪策略下的定轨预报精度可知，两站接力跟踪策略因为测量数据较少、几何约束弱等原因，无法保证分离点高精度的定轨预报要求，三站接力跟踪策略的定轨精度较优，在位置误差及速度误差上均优于双站接力跟踪策略定轨精度一个量级以上。这说明三站接力跟踪策略的测控策略可以较好地满足返回器分离前的定轨精度需求，为再入返回器返回分离前的测控弧段测站布局及时间分配提供依据和借鉴。

（References）

［1］欧阳自远.我国月球探测的总体科学目标与发展战略［J］.地球科学进展，2004，19（3）：351-358 Ouyang Ziyuan.Scientific objectives of Chinese lunar exploration project and development strategy［J］.Advance in Earth Sciences，2004，19（3）：351-358（in Chinese）

［2］陈明，唐歌实，曹建峰，等.嫦娥一号绕月探测卫星精密定轨实现［J］.武汉大学学报（信息科学版），2011，36（2）：212-217 Chen Ming，Tang Geshi，Cao Jianfeng，et al.Precision orbit determination of CE-1 lunar satellite［J］.Geomatics and Information Science of Wuhan University，2011，36（2）：212-217（in Chinese）

［3］陈明，张宇，曹建峰，等.嫦娥二号探测器轨道确定与测轨技术［J］.科学通报，2012，57（9）：689-696 Chen Ming，Zhang Yu，Cao Jianfeng，et al.Orbit determination and tracking technology of CE-2 satellite［J］. Chinese Science Bulletin，2012，57（9）：689-696（in Chinese）

［4］段建锋，张宇，陈明，等.嫦娥三号姿轨控过程中GRAIL重力场模型的应用［J］.飞行器测控学报，2014，33（4）：342-347 Duan Jianfeng，Zhang Yu，Chen Ming，et al.Application of GRAIL lunar gravity field model in attitude and orbit control for CE-3 satellite［J］.Journal of Spacecraft TT&C Technology，2014，33（4）：342-347（in Chinese）

［5］张磊，谢剑锋，刘勇.绕月返回飞行再入航程调整的轨道控制［J］.飞行器测控学报，2015，34（1）：64-69 Zhang Lei，Xie Jianfeng，Liu Yong.Trajectory maneuver for reentry downrange modification during circumlunar return flight［J］.Journal of Spacecraft TT&C Technology，2015，34（1）：64-69（in Chinese）

［6］贾世锦.载人登月返回再入有关问题初步研究［J］.航天返回与遥感，2011，32（2）：18-25 Jia Shijin.Preliminary study on the return and re-entry of manned lunar landing［J］.Spacecraft Recovery& Remote Sensing，2011，32（2）：18-25（in Chinese）

［7］张宇，王健，段成林，等.基于我国深空站三向测量模式的数据精度分析［J］.飞行器测控学报，2014，33（3）：268-274 Zhang Yu，Wang Jian，Duan Chenglin，et al.Analysis of the data accuracy of the three-way measurement mode of China's deep space station［J］.Journal of Spacecraft TT&C Technology，2014，33（3）：268-274（in Chinese）

［8］黄磊，王宏，樊敏.三向测量技术在深空探测中的应用研究［J］.飞行器测控学报，2012，31（3）：6-10 Huang Lei，Wang Hong，Fan Min.Application of three-way measurement in deep space exploration［J］. Journal of Spacecraft TT&C Technology，2012，31（3）：6-10（in Chinese）

［9］Escoubet C P.Cluster-Ⅱ：scientific objectives and data dissemination［J］.ESA Bulletin，2000（102）：54-60

［10］陈茹梅，刘齐，单琦，等.统一S频段测控系统残余载波快速捕获方法［J］.航天器工程，2014，23（4）：62-65 Chen Rumei，Liu Qi，Shan Qi，et al.Quick acquisition method of residual carrier in USB TT&C system［J］.Spacecraft Engineering，2014，23（4）：62-65（in Chinese）

［11］汤锡生，陈贻迎，朱民才.载人飞船轨道确定和返回控制［M］.北京：国防工业出版社，2002 Tang Xisheng，Chen Yiying，Zhu Mincai.Orbit determination and reentry control for manned spacecraft［M］.Beijing：National Defense Industry Press，2002（in Chinese）

［12］胡松杰，唐歌实.北京中心深空探测器精密定轨与分析软件系统［J］.飞行器测控学报，2010，29（5）：69-74 Hu Songjie，Tang Geshi.BACC orbit determination and analysis software for deep-space explorers［J］.Journal of Spacecraft TT&C Technology，2010，29（5）：69-74（in Chinese）

［13］李济深.人造卫星精密轨道确定［M］.北京：解放军出版社，1995 Li Jishen.Satellite precise orbit determination［M］. Beijing：People's Liberation Army Press，1995（in Chinese）

（编辑：夏光）

Analysis of Reentry Capsule Orbit Determination Precision Using Multiple Station Relay Tracking Strategy

DUAN Jianfeng1，2XIE Jianfeng1，2ZHANG Yu1，2CHEN Ming1，2DUAN Chenglin1，2WANG Zhenyu1
（1 Beijing Aerospace Control Center，Beijing 100094，China）
（2 Science and Technology on Aerospace Flight Dynamics Laboratory，Beijing 100094，China）

In the case of inability to achieve three-way measurements of the reentry capsule，and for meeting the return accuracy requirements of the Chinese lunar reentry capsule before separation，this paper provides a measurement strategy of relay tracking for multiple stations to solve the problem of precision.The strategies of relay tracking for two stations and three stations is developed with the arc of the re-entry test task before the separation，and the SAMBA satellite is used as an example to analyze the multiple station relay tracking data.The analysis results show that the optimal strategy of the orbit prediction precision is the three station relay tracking which is able to achieve reliable and safe reentry.This conclusion can provide a recommendation for the tracking strategy on the upcoming reentry mission before separation.

reentry capsule；multiple station relay tracking；SAMBA satellite；experiment of orbit determination；precision analysis

V412.41

：ADOI：10.3969/j.issn.1673-8748.2015.05.006

2014-10-08；

：2015-06-16

国家自然科学基金（11173005，11073047，11203003）

段建锋，男，助理工程师，研究方向为航天器精密定轨。Email：duanjf1987@sina.com。