改进的小波包能量分段阈值降噪方法

钟孟春，张春林，李 华，王宝琦

装甲兵工程学院，北京 100072

1 引言

在对机械设备进行状态监测与故障诊断时，通常会对设备的振动信号进行处理。但是，振动信号中往往夹杂着很多噪声，这对振动信号的特征提取造成了很大的麻烦。所以，在进行振动信号处理前，首先要对信号进行降噪处理。小波和小波包降噪方法由于其具有低熵性、多分辨率等优点，在信号降噪中得到了广泛的应用[1]。

小波和小波包降噪的核心是如何选取阈值和阈值函数。常用的小波包降噪阈值主要有Sqtwolog规则阈值、Rigrsure规则阈值和Minimaxi规则阈值。以上三种阈值降噪的效果各不相同，其中Minimaxi与Stein阈值规则降噪较为保守，是将部分系数置零，不容易丢失真实信号成分，Sqtwolog固定形式的阈值降噪能更有效地去除噪声。对于低频信号，由小波包分解后，有用信号主要分布在低频段，且频率段能量值一般较高，而噪声均匀分布在整个频率段上，且频段能量值一般较低。所以不同频段的小波包分解系数对关心的有用信号和不关心的噪声信号有着不同的反映。因此，用同一阈值对整个频率段的小波包系数进行阈值处理显然是不合适的，不能得到理想的效果。

据此，需要对不同的频段采取不同的阈值进行处理。文献[2]中的SMS法采用分段阈值处理时，对频率段的分段较为粗糙，只是固定地对小波包分解后第一个节点采用Rigrsure规则阈值，最后一个节点采用Sqtwolog规则阈值。这种分段阈值处理形式虽然较全局阈值处理有了一定的改善，但是对实际振动信号中有用信号的保护与噪声的去除效果不是非常理想。本文研究提出了一种更实际有效的小波包分段阈值降噪方法，重点在于频段的划分。由于频段划分基于能量，因此命名为最优小波包能量分段阈值降噪方法（Best Wavelet Packet Energine Subsection threshold De-noising），简称BWPES。

2 小波包去噪理论概述

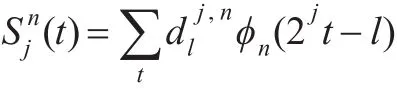
由于

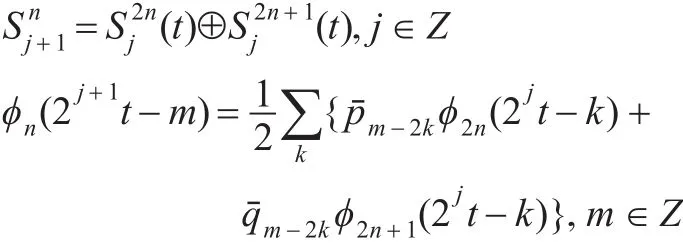
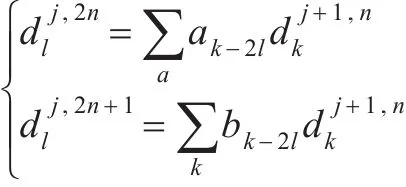
由小波包两尺度关系：

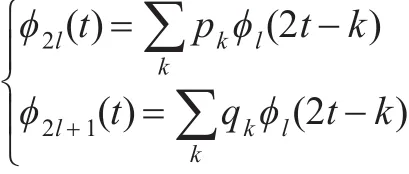
可得到由(t)与重构的重构算法。小波包的重构算法为：

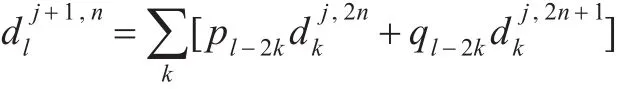
以小波包三层分解为例，其小波包分解树如图1所示。

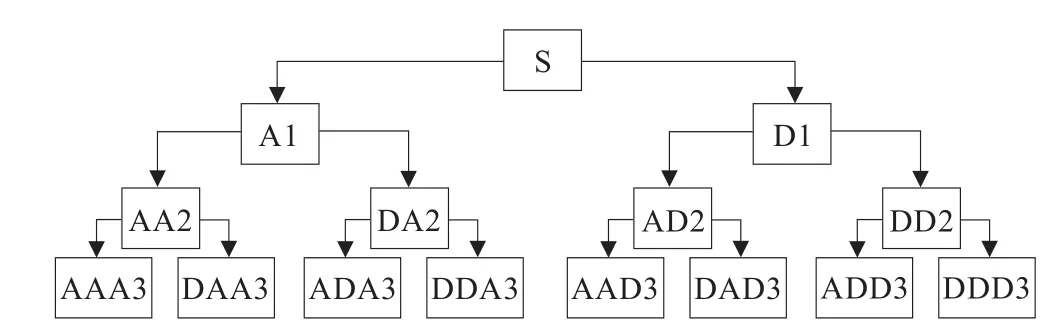
图1 三层小波包分解树

图1中，A表示低频，D表示高频，末尾的序号数表示小波包分解的尺度数，分解具体如下关系：

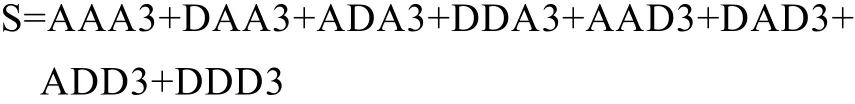
小波包阈值去噪过程一般按如下步骤[3]进行：

（1）选择合适的小波与分解层次，进行小波包分解。（2）确定最优小波包基，计算最优树。

（3）选择一个适当的阈值，对小波包分解系数的阈值进行量化。

（4）小波包重构。

其中最关键的还是阈值的选择和阈值量化，它们直接关系到对信号进行降噪处理的质量。

3 改进的小波包能量分段阈值降噪方法

3.1 小波基的选择原则

小波包阈值去噪的第一步是选择合适的小波函数对信号进行小波包分解，可见小波基的选择对去噪性能是有重要影响的。首先，信号经小波包分解后得到的小波系数越稀疏（即越多的小波系数接近零），越有利于去噪；其次，不通过的小波基重构得到的信号，也直接影响到降噪效果[4]。

选择分解小波时，一般选择消失矩高，支撑尺寸小的小波基。消失矩越高，小波包分解的平滑项系数越接近零；支撑尺寸越短，越有利于信号奇异点的定位，可使较大的小波系数落在小波支撑尺寸内。

选择重构小波时，一般选择正则性高，对称性好的小波基。这样的小波基光滑性强，频域局部性好，有利于消除由阈值处理后得到的小波系数所引入的误差。

3.2 小波包分解并按频率顺序排列

小波包分解的过程实质上是通过一组高/低通共轭滤波器的滤波以及“隔点重采样”过程，而高通滤波所得到的信号采样时，会导致频率折叠。因此，小波包算法就出现了频带错位问题，所以，首先需要对错位的频带进行排序。文献[5]给出了小波包频率的排序，即：每次通过低通滤波，直接频段2分频，经过高通滤波器，频段2分频并取反。下面以3层小波包分解举例，其频率排序如图2所示。

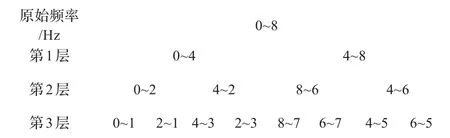
图2 3层小波包分解实际频率排序

图2所计算的小波包频率排序与仿真软件MATLAB中的小波包分解频率排序是一致的。

3.3 最优小波包节点能量与分段阈值去噪

为了能更好地去除噪声，本文采取最优小波包节点能量与分段阈值相结合的去噪方法。根据最优小波包基各节点能量的大小，判断是否含有有用信号，并将其分为有用信号段、过渡段和噪声段。

对于高频噪声段，采用去噪力度相对较大的Sqtwolog规则进行阈值去噪，最大程度地去除噪声。对于剩下的小波包，计算各个小波包节点的能量Ei，为了使不同的分解层数的小波包具有可比性，采用Ei/25-j（以5层小波包分解为例）表示各节点的能量，其中i代表节点编号，j代表节点所在层数，并把节点能量按大小排序。

小波包的能量越高，表示对应的频段中有用信号的成分越大；反之，说明噪声成分更大。据此，可以按照能量值的大小确定信号段与过渡段的分界。这里需要指出的是，这里所谓的分界其实并不是严格意义上的分界，根据实际情况的不同，需要根据经验给出相对较合理的分界条件。下面以Matlab自带的Doppler信号为例，根据小波函数的选择原则，经过对比分析之后，选择db4小波作为分析小波，对信号进行5层小波包分解，并且计算它的最优小波包基，对其能量排序，取能量最低的4个小波包，求其能量的平均值Ea，当某个小波包的节点能量大于n（n≥2，由经验给出）倍Ea时，认为该频段为有用信号段，采用Rigrsure阈值规则进行阈值去噪。剩下的小波包节点即为过渡段，使用Minimaxi阈值规则进行阈值去噪。这里需要指出的是，此方法并不是适用于所有的振动信号，n≥2的条件也等同于信号的SNR≥3，当信号的SNR＜3或者信号是纯噪声时，此方法的降噪效果并不理想。所以在信号降噪之前，首先要对信号给出判断，以及信噪比的估计，根据估计给出经验值n。

总的来说，对信号首先用小波包分解，并且结算它的最优小波包基。将分解后的小波包节点按频率大小进行重排序，对于高频段的小波包节点，直接对其用Sqtwolog规则进行阈值去噪。对于低频段的小波包节点，通过进行能量排序，划定有用信号段和过渡段的分界。对于有用信号段，采取Rigrsure阈值规则进行阈值去噪，对于过渡段，采取Minimaxi阈值规则进行阈值去噪。通过这种方式，经行阈值降噪，有效地提高了降噪的可靠性，极大程度地保留了有用信号。

4 基于matlab软件的去噪仿真

为了验证BWPES算法的有效性和优越性，以MATLAB（R2010a）作为平台，对Matlab自带的噪声测试信号Doppler信号进行测试仿真，Doppler信号属于非线性非平稳信号，和需要处理的信号较接近，有利于反应实际信号的处理效果。

为了能定量对比不同降噪方法的降噪效果，需要引入小波去噪效果的评价方法。常用的评价指标有信噪比（SNR）、均方根误差（RMSE）和平滑度指标。

信噪比是测量信号中噪声量度的传统方法，它的计算公式[6]为：

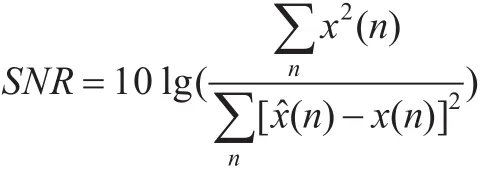
均方根误差是指原始信号与去噪后的估计信号之间的方差的平方根，它的计算公式[7]为：

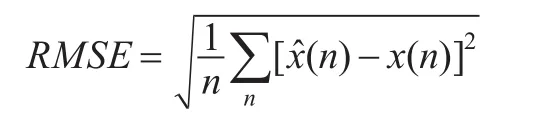
由于信噪比在评价去噪指标时，有时不能完全反应去噪的效果，还引入了平滑度函数，它在评价去噪效果时，表现更好，它的计算公式[8]为：

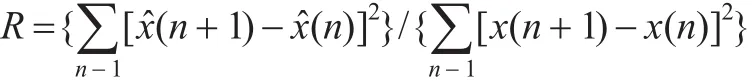
式中，x(n)为原始信号；(n)为经小波包降噪后的估计信号；n为信号长度。

下面分别用Rigrsure准则、Sqtwolog准则、Minimaxi准则、小波Wden自动去噪以及文献[5]中的SMS阈值降噪方法与本文提出的BWPES降噪方法进行对比分析。为了使结果对比更具可靠性，在使用不同方法进行阈值降噪的过程中，使用统一的小波基函数、阈值函数和小波分解层数，如图3～9。

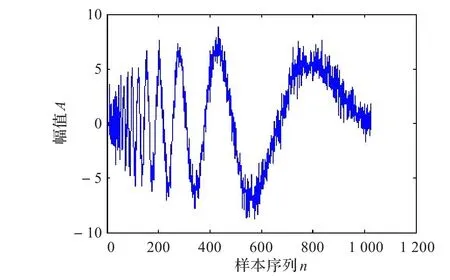
图3 Matlab中的noisdopp信号

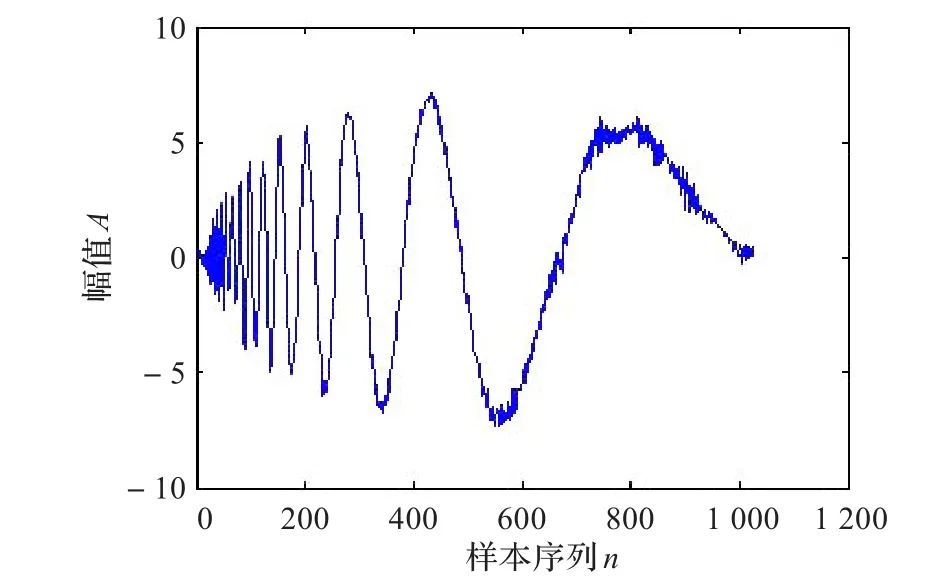
图4 Rigrsure准则降噪后信号

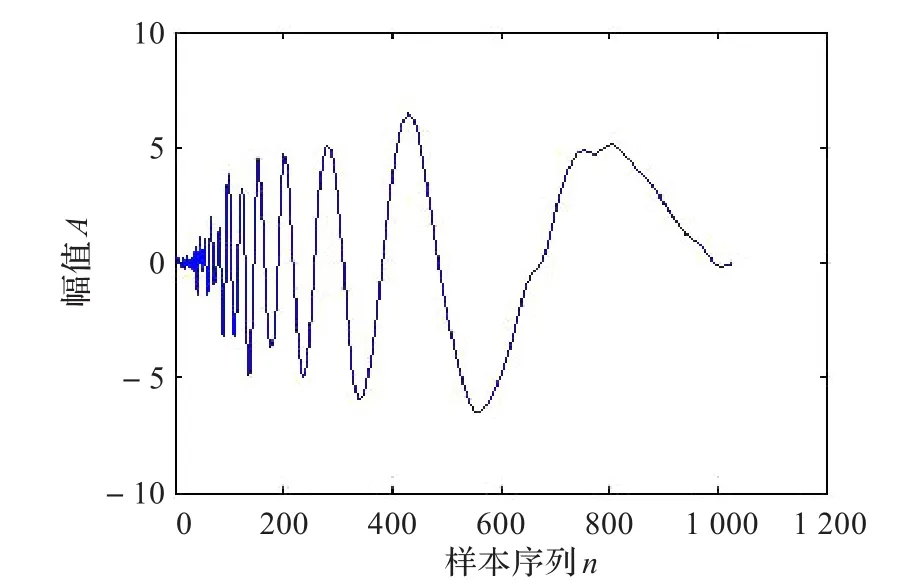
图5 Sqtwolog准则降噪后信号

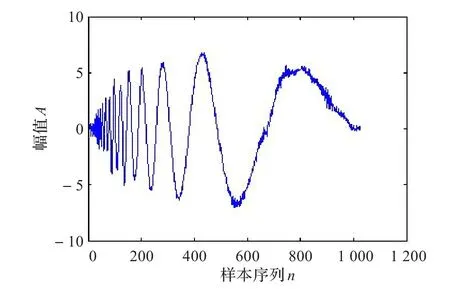
图6 Minimaxi准则降噪后信号图

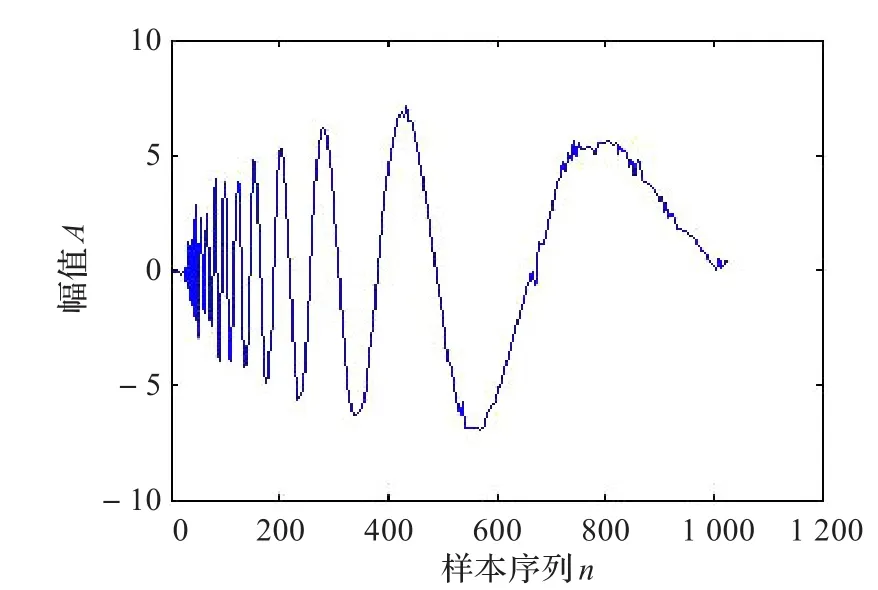
图7 小波Wden自动降噪后信号

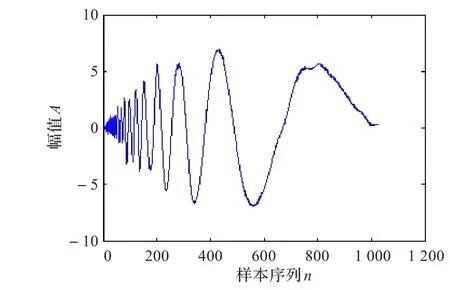
图9 BWPES降噪后信号

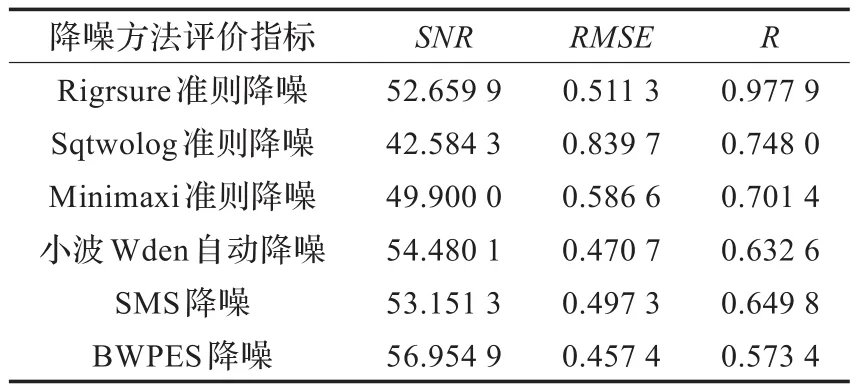
表1 降噪效果对比

通过不同降噪方法的效果对比，不难发现，虽然各种不同的方法都起到了一定作用的降噪效果，但是由于Rigrsure和minnimax阈值选取规则比较保守，仅将部分系数置零[9]，因此在信号去噪的过程中，噪声去除不够彻底。Sqtwolog阈值选取规则是选用固定的阈值，相对去噪力度较大[10]，在去除高频噪声的同时，把高频段的信号也同时去除了。小波Wden自动降噪的实质也是根据信号的特点选择一种单一的阈值选取规则[11]，因此也无法避免单一阈值选取所带来的负面影响，而文献[2]中提出的方法虽然避免了单一阈值选取带来的不利影响，但是降噪效果仍然不是很理想。在此基础上，本文提出了最优小波包能量分段阈值降噪方法，通过计算最优小波包的能量，并依据能量进行分段去噪，不仅能最大程度地去除噪声，而且还能分辨出高频信号和高频噪声，大大提高了小波包降噪的可靠性。

5 结束语

本文通过比较不同的阈值选取规则进行小波包降噪的效果，指出了各自存在的缺点，提出了最优小波包能量分段阈值降噪方法，并跟其他小波包降噪方法进行对比分析，得出最优小波包能量分段阈值降噪方法明显优于其他小波包降噪方法，在机械设备的状态监测和故障诊断中可以运用此方法，这将大大提高特征提取的准确性。

本文的降噪方法在高SNR信号降噪中取得了较好的效果，但是并不是适用于所有的振动信号，信号降噪的另一个关键问题是噪声估计，过多的噪声估计和过少的噪声估计都将不利于有用信号从被噪声污染的信号中提取出来。所以，如何更加精确地进行噪声估计是下一步需要努力研究的方向。

[1]谭文才，张秋菊.小波包多阈值去噪的一种改进[J].江南大学学报：自然科学版，2012，11（2）：178-181.

[2]郭晓霞，杨慧中.基于多阈值的小波包去噪[C]//第27届中国控制会议.北京：北京航空航天大学出版社，2008.

[3]Daubechies I.Ten lectures on wavelets（CBMS-NSF regional conf series in appl math）[M].Philadelphia：Society for Industrial and Applied Mathematics，1992.

[4]魏宝琴，李白萍.最有小波基的选择原则[J].甘肃科技，2007，23（10）.

[5] 纪跃波.小波包的频率顺序[J].振动与冲击，2005，24（3）：97-99.

[6]吴富梅，杨元喜.基于小波阈值消噪自适应滤波的GPS/INS组合导航[J].测绘学报，2007（2）.

[7]林渊，肖峰，郑宾，等.小波变换阈值降噪方法及其在武器自动机数据处理中的应用[J].电子测量技术，2009，32（1）：128-130.

[8]王翔，葛晓霞.基于小波变换的汽轮机振动信号软阈值消噪技术研究[J].汽轮机技术，2009，51（3）：204-206.

[9]田玉静，左红伟.小波消噪阈值算法优化[J].声学技术，2009，28（4）：503-506.

[10]李双，叶威.小波消噪在测试信号处理中的应用[J].理论与实践，2011，31（2）：4-8.

[11]刘文艺，汤宝平，蒋永华.一种自适应小波消噪方法[J].振动、测试与诊断，2011，31（1）：74-78.