基于DEA模型的省会城市经济辐射程度研究——以山东济南为例

叶金龙

(安徽财经大学,安徽蚌埠233000)

基于DEA模型的省会城市经济辐射程度研究
——以山东济南为例

叶金龙

(安徽财经大学,安徽蚌埠233000)

在山东省范围内,以济南为经济中心，利用引力模型计算的R强度值和DEA模型研究省会城市对周边地区经济辐射程度,研究发现省会城市对周边地区的经济扩散程度随着距离辐射中心的增加在不断减弱。创新之处在于利用DEA模型确定出具体有效辐射范围的新方法。这一结论不仅有利于研究多地区经济之间的相互影响程度,更便于政府以及相关部门为经济共同发展提出有效措施和科学建议。

引力模型;R强度值;经济辐射程度;DEA模型;有效辐射范围

一 问题的提出

早在十六大报告中,就提出了共同发展的宏观经济目标。但是由于经济基础、地理位置、自然资源和国家政策等因素的差别,各个地区经济发展水平存在着明显的差异,因此在同一时间实现经济共同发展的目标是相当困难的。济南作为山东省的省会城市,受到国家的大力扶持,其经济发展速度逐年稳步加快并明显快于周边地区。为了实施经济共同发展的政策,提高人们生活水平,周边地区的经济发展不容忽视。本文以济南为经济中心,以研究经济较发达地区对周边地区经济辐射程度的大小,确定出济南具体经济的有效辐射范围为目的。

目前,在经济中心对周边地区经济发展拉动效应的研究方面,国内许多著名学者通过具体实证分析得到很多可靠结论。浦承嵩,李红(2010)利用协方差法,研究上海中心对周边地区经济辐射效应以及市场的带动效应,结论表明,上海对周边城市具有明显经济辐射效应和市场带动效应。[1]朱虹(2012)利用空间计量回归方法,研究比较北京和上海两大中心城市经济辐射效应的差异,结论表明,北京对周边地区的辐射模式主要以空吸效应为主,而上海则以反哺效应为主。[2]上述文献表明,经济中心对周边城市的经济发展具有有效的辐射效应,能够拉动周边地区经济发展,实现共同发展的宏观目标,但并没有得出其有效经济辐射范围的界限和大小。本文利用引力模型和DEA模型解决了这一问题,引力模型的引入确定了经济中心对周边地区存在的经济辐射效应,而DEA模型对引力模型结论进行验证并界定出经济中心具体的经济有效辐射范围。

二 引力模型对省会城市经济辐射程度的分析

(一)模型建立

从引力模型应用于经济辐射效应领域以来,引力模型的实用性不断增强,模型也逐渐被改进完善,使其在经济研究中占据着较为重要的地位。引力模型最初形式原理相对简单,即引用物理学上两点之间的相互作用力作为引力模型的一般形式[5]：

其中,Tij为两点之间的相互作用力,表示运动物体的质量,d则为两运动物体之间的距离。由于该模型未知参数较多,并不能直接应用于经济领域研究。孟德友,陆玉麒(2009)通过对江苏区域经济研究,将作为代表一个区域经济发展水平的量化指标,d则代表两地区间的距离。将此模型改进为可以测度经济中心对周边城市经济辐射程度的量化模型,[6]即：

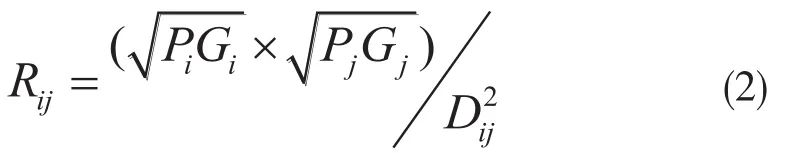
在上述模型中,Rij强度值表示为经济中心地区对其经济辐射程度的具体数值,Pi表示该地区的人口总数,Gi则表示该地区的GDP值,Dij表示两地区间距离。PiGi指用人口总数与生产总值的乘积表示该地区经济发展强度的大小,上述模型对距离进行平方,不仅增加了模型的整体平衡性,更体现了两运动物体间作用力在模型使用上的科学性。

(二)数据准备

模型中用到的指标有各个地区生产总值,人口总数和各地区距经济中心济南间距离查找找2009-2012年间统计年鉴,得到模型各个指标在上述4年间的具体数值。

(三)引力模型应用与分析

由上文得到操作模型的具体指标值后,为计算方便,该模型用matlab软件对结果进行求解。将生产总值记作G,G0表示济南的生产总值,G1,G2,G3,G4,G5,G6,G7,分别表示泰安,淄博,聊城,济宁,荷泽,日照,烟台各地区的生产总值;把各地区的人口总数记作P,P0表示济南的人口总数,P1,P2,P3,P3,P4,P5,P6,P7分别表示泰安,淄博,聊城,济宁,荷泽,日照,烟台各地区的人口总数;d1,d2,d3,d4,d5,d6,d7分别表示济南到泰安,淄博,聊城,济宁,荷泽,日照,烟台各地区的距离。F1,F2,F3,F4,F5,F6,F7则分别表示济南对泰安,淄博,聊城,济宁,荷泽,日照,烟台各地区的经济辐射程度值,记作Rij。

在假设山东各个地区经济发展水平不受省外经济影响的条件下,利用改进的引力模型和matlab软件对数据进行操作[8],整理结果做如下表格：

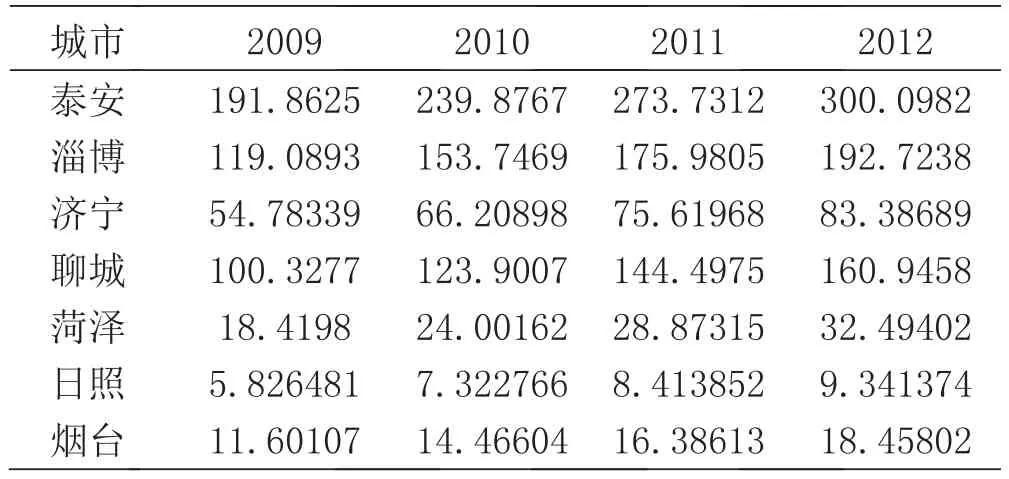
表1 济南对各地区的R强度值

烟台市因为优越的地理环境和丰富的自然资源,加之国家政策支持,经济发展快于其它省内地区。本文将烟台作为异常值引入,主要目的是探索以济南为经济中心的前提下,和其它距离相近的地区相比,济南对其经济辐射程度是否与其它地区存在着明显的差异。由表1的R强度值可知,距离最近的泰安受到济南的经济辐射的程度是最显著的,在2009年达到了191.8625,与各个地区同期相比,受到的辐射影响是最大的,随着各个地区经济联系密切程度不断加强,其经济辐射程度也在逐渐增大,从2009的191.8625上升到2012的300.0982,较之其它地区增速最快。相比之下,距离济南最远的日照地区所受到的经济辐射程度是最小的,2009年只有5.8265,到2012年也只是刚刚达到9.3413,并且增速是所有地区中最缓慢的。介于泰安和日照之间的其它地区,受到以济南为经济中心的经济辐射程度的数值全部介于两者的R强度值之间,随着经济发展的加快,其R强度值也在不断增大。距离经济中心越近的地区,其R强度值的增速也比较远地区要快。作为异常值的烟台,其R强度值仅比同等距离的日照地区大,而且优势并不明显。这说明即使自身经济较发达,当达到一定的距离后,所受到其它发达地区的经济辐射程度也是较小的。

图1 济南对周边地区的经济辐射程度

由图1显示,距离所研究的经济中心济南最近的泰安地区受到济南经济辐射的程度最大,数值在各年间远大于其他地区,2009-2012年间经济辐射的R强度值不断增大且每年的增速不断加快,说明济南与泰安地区的经济有着密切的联系,济南对泰安的经济辐射使得该地区经济发展速度明显加快,逐步被同化,有望实现共同发展的经济目标。距济南较远的淄博,聊城,济宁地区,由于距离的进一步增大,受到经济中心的经济辐射程度逐渐减小,表明实际中的经济拉动效应也在不断减弱,但是由于省内总体经济快速发展的带动下,对这些地区的经济辐射程度却在逐年增加。烟台经济发展水平处在省内最高层次,自身发展优于其它地区,但是,其受到济南经济辐射的程度基本和同距离的日照地区持平,济南对其经济拉动效应是不显著的。总体而言,经济中心对周边地区的经济辐射程度随着距离的增大在不断减弱,经济的拉动效应不断减小。

三 DEA模型对影响R强度值的指标评价分析

(一)DEA模型的引用

1978年,著名的运筹学家A.Charnes,W.W.Cooper,及E.Rhodes首先提出了数据包络分析的方法,用于评价部门之间的相对有效性。[9]本文中应用的DEA模型为VRS模型,即从一般模型中的技术效率分解为纯技术效率和规模效率,并且技术效率是纯技术效率与规模效率的乘积。[10]形式如下：

本文引入VRS模型,以此评价影响经济辐射程度R强度值的各个指标,衡量各个指标是否有效,利用模型得到的全要素相对生产率对单个指标进行优化,分析每个指标对R强度值的影响程度。通过此模型即可以评价指标的有效性,还可以对引力模型分析得到的结果进行验证,进一步分析确定济南对周边地区经济的有效辐射范围。

(二)数据准备

根据引力模型结构可知,决定经济辐射程度R强度值的指标有该地区的人口总数,生产总值和距离经

济中心济南的距离。将上述3个指标作为DEA模型的投入指标,R强度值作为产出指标,即可进行VRS模型的分析。由引力模型结论可知,2009-2012年间的经济辐射程度R强度值中,2012年各个地区的R强度值差别是最明显的,因此,这里采用2012年3项指标的数据作为投入指标的具体值更能够显著的得到济南对各个地区经济辐射程度的大小以及有效范围。

(三)VRS模型应用与分析

基于Input-DEA模型,在产出一定的情况下,以此衡量实际投入与最小投入之差,评价确定出有效投入包络面,[11]即可界定经济中心的有效辐射范围。将上述提到的8个城市作为样本,确定1个产出指标3个投入指标,利用MULTI-STAGE通过VRS模型得到结果如下统计表：

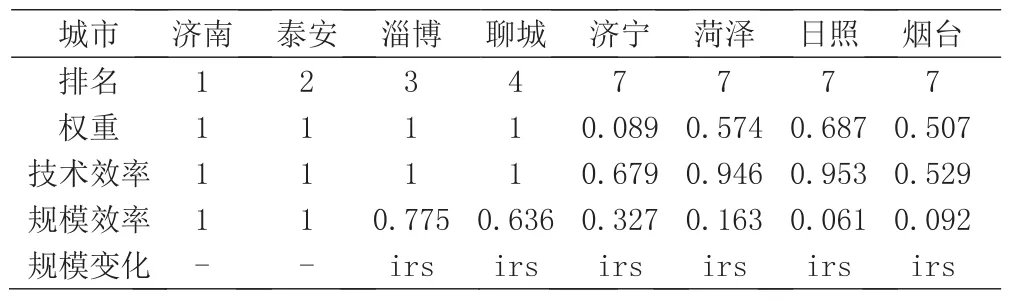
表2 VRS模型结果统计表

对各个地区3个指标的建模分析结果表明：从排名角度分析,排在前4位的依次是济南,泰安,淄博,聊城。对比引力模型的结论,由VRS模型得到的结论与之相一致,进一步验证了引力模型结果的有效性。后4位的城市排名一致为7,表明济南对该地区的经济辐射程度不再显著有效,即对其经济影响效应较弱,评价投入指标不再有效,单个指标需要一定的优化才能达到模型的最高效率性。[12]因此,排名前4位的城市权重为1,即处在经济中心的有效辐射范围内,而济宁,荷泽,日照3个地区随着距离不断增加,指标需要调整权数也在不断增大,经济辐射程度越来越不显著,超出了其有效经济辐射范围。VRS模型的纯技术效率与权重的走势相一致,都受到烟台作为异常值的影响,说明经济中心的有效辐射范围会受到外界经济环境影响且无法全部排除,但能够合理控制。从规模报酬角度考虑,泰安受到济南的经济拉动效用最有效,规模报酬不变,但是随着距经济中心距离的增加,规模效率不断降低,在整体经济背景下,总体经济趋于上升趋势,规模报酬全部递增,[13]即符合引力模型所得结果,也满足实际经济情况。

表3为VRS模型自动调整后的有效指标值。由下表总体而言,排名前4位即权重为1的地区指标已经有效显著,故表中数值保持不变。排名后4位的地区由于没有达到单个指标的技术效率有效显著,通过权重进行调整,使其满足相对有效。如下表结果所示：

排在5-8名的地区由于存在非DEA有效,其3个投入指标均通过权重进行调整。随着排名权重的增大,人口总数的削减比例上升,说明这些地区人口总数过大,劳动力过剩影响了经济的增长,合适的人口比例能够有效的促进该地区经济的发展。而日照地区存在劳动力不足的情况,因此人口总数在模型调整后出现增加的情况。就生产总值而言,非DEA有效地区均出现生产不足的现状,应该积极促进经济发展。

本文通过经济中心对不同距离地区经济辐射程度测度,由DEA有效性判定出济南对周边地区经济的有效辐射范围。如表3距离所示,当样本属于DEA有效时,距离权重为1。因此,当该地区不存在DEA有效时表明济南对其经济的有效辐射范围不再显著。排名5-8位的地区均存在距离被调整的情况。离济南最近的存在非DEA有效的地区是济宁,距济南188公里,由此可得,济南对周边地区经济的有效辐射范围界定在113-188公里之间。

表3 投入指标有效调整统计表

四 结论与政策建议

(一)主要结论

本文结论与大多数同类研究所得结果相一致,经济中心对周边地区都存在一定经济辐射效应。但本文的创新点在于利用DEA进行验证并评价影响指标的有效性,得到了经济的有效辐射范围。

通过引入经典的引力模型即上述公式(2),利用该地区的生产总值,人口总数和距经济中心济南距离3个指标得到经济辐射程度的R强度值,直观的看出经济中心济南对周边地区的经济辐射程度的大小。随着距离济南越来越远,则该地区受到济南经济辐射的程度不断降低,在实际中的表现为经济发展水平相对落后与距离济南较近的地区。济南对该地区经济拉动作用逐渐不在显现。对比加入的异常值而言,虽然R强度值略高于同距离的地区,但是经济辐射效应也不显著。下图2为各地区城镇居民年收入,可进一步验证结论的有效性。在2010-2012年间各个地区的城镇居民年收入都呈现上升趋势且同比速度不断增加。纵向比较可知,就2010年而言,济南地区城镇居民年收入值最大,但是随着距离济南越来越远,各个地区的数值基本呈现下降趋势,各年数据均呈现出这种走势,进一步验证了引力模型结论的合理性。

DEA模型的使用,不仅进一步验证了引力模型所得结果的准确性,还运用VRS模型对引力模型各个投入指标进行有效性评价。当出现非DEA有效

时,经济拉动效应不在显著有效,[15]由此得到经济的有效辐射范围。对指标DEA评价表明,距离济南较近的前4位地区是DEA有效的,济南对该地区有明显的经济拉动效应。而排名后4位的地区均属于非DEA有效,需要VRS模型进行有效的调整。通过DEA模型定出经济的有效辐射范围,对各个地区经济发展具有科学的参考价值。

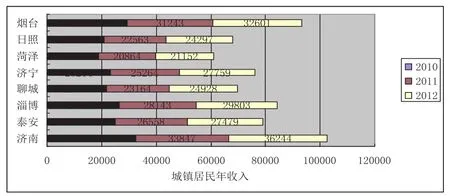
图2 各地区城镇居民年收入

(二)政策建议

本文所得结论对各地区经济发展具有科学的借鉴意义和指导方向。根据影响经济辐射程度的指标提出以下几条可行建议。

1.合理控制本地区人口总数。

由结论可知,当该地区处于非DEA有效时,人口往往会影响本地区经济的发展。人口总数超出一定范围,就会导致劳动力过剩,失业率上升,人均生活水平降低,造成不合理的发展状况。而当人口总数不足时,又会使得劳动力不足,阻碍经济发展,降低整体发展水平。因此,将人口总数控制在合理范围内不仅不会出现影响经济发展的状况,还能保证经济的合理有效,可持续发展。

2.加强与周边地区经济联系。

经济发达地区对周边城市的经济拉动是持续存在的,保持与周边地区经济发展的联系,保持对外开放状态,有利于吸收和引进其它地区高效的经济发展模式。对自身经济进行结构性调整,取长补短,利用与外部的联系,发挥自身优势,促进经济的同步发展。

3.缩短与发达地区的时间距离。

本文最重要的结论是,随着距离经济中心越来越远,该地区受到经济辐射程度越来越小,拉动效果不显著。因此,应该大力发展该地区的交通运输业,在时间上缩短与周边地区的距离。例如,如今多地正在筹建高铁,不仅方便人们的出行,更有利于促进经济的发展。

4.努力提高居民收入水平。

由图2对本文的结论进行验证可知,居民的收入水平与该地区的经济发展水平趋势是相一致的。因此,为了促进经济的快速发展,应该大力提高居民就业率,合理利用人力资源。吸引外地投资,不断创新,提升就业机会。努力改善居民的收入水平,促进经济的共同发展。

[1]浦承嵩.李红,都市圈经济辐射效应的协方差分析[J].经济研究导刊,2010(2):74-76.

[2]朱虹,空吸抑或反哺：北京和上海的经济辐射模式比较[J].世界经济,2012(3):111-124.

[3]马赛赛,滨海新区与环渤海城市群经济发展梯度与辐射效应研究[J].时代金融,2013(11):127-128.

[4]邱红,中心城市对周边区域房地产市场辐射效应探究[J].合作经济与科技,2014(02):10-11.

[5]魏后凯,现代区域经济学[M].北京:经济管理出版社,2006,420-430.

[6]孟德友,陆玉麒.基于引力模型的江苏区域经济联系强度与方向[J].地理科学进展,2009(5):697-704.

[7]2009-2012山东统计年鉴[M]:北京:中国统计出版社.

[8]吴礼斌.经济数学实验与建模[M].天津:天津大学出版社,2009.

[9]Charnes A,Cooper W W,Rhodes E.Measuring the efficiency of decision making units[J].European journal of operational research,1978,2(6):429-444.

[10]Banker R D,Charnes A,Cooper W W.Some models for estimating technical and scale inefficiencies in data envelopment analysis[J].Management science,1984,30(9):1078-1092.

[11]魏权龄,卢刚.DEA方法与模型的应用:数据包络分析[J].系统工程理论与实践,9(3):67-75.

[12]彭煜.DEA有效性的梯度及应用[J].西南工学院学报,1997:10-88.

[13]曾珍香,顾培亮.DEA方法在可持续发展评价中的应用[J].系统工程理论与实践,2000(8):114-118.

[14]魏权龄.评价相对有效性的数据包络分析模型:DEA和网络DEA[M].北京:中国人民大学出版社,2012.

［责任编辑鲁海菊］

On Economics Radiation of Provincial Capital Cities from the Perspective of DEA Model

YE Jin-long
(Anhui University of Finance and Economics,Anhui Bengbu 233000,China)

As the economic center of Jinan,this paper use intensity values of Gravity Model by calculated and DEA Model in order to research the economic radiation effects of capital city on the surrounding area in the range of Shandong Province.Study found that the economic radiation effects of capital city on the surrounding area become weakening with the increase in the distance.And using the DEA Model to determine the effective radiation range.This conclusion is not only conducive to research the mutual economic impact within different areas,but also easier for Government and relevant departments to come up with effective measures and scientific advice in order to keep the common development of economy.

Gravity model；R intensity value；Economic radiation；Intensity value；DEA model；Effective radiation range

F29

A

1008-9128(2015)05-0060-04

2014-12-10

叶金龙(1991-),男,安徽安庆人,硕士生,研究方向：贸易经济,区域经济的研究。