第二类r-置换因子循环矩阵的逆与广义逆

胡　艳

(西安培华学院 基础部， 陕西 西安 710125)

第二类r-置换因子循环矩阵的逆与广义逆

胡艳

(西安培华学院 基础部， 陕西 西安 710125)

摘要：给出了第二类r-置换因子循环矩阵的概念，利用特殊矩阵，得到f(x)、g(x)的公因式d(x)，根据公因式的取值进而得到第二类r-置换因子循环矩阵的逆与广义逆，并给出了具体的计算公式.

关键词：第二类r-置换因子循环矩阵；第二类r-置换因子循环矩阵的逆；广义逆

0引言

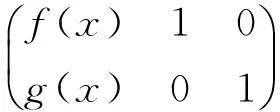
1基本概念

我们给出如下定义：

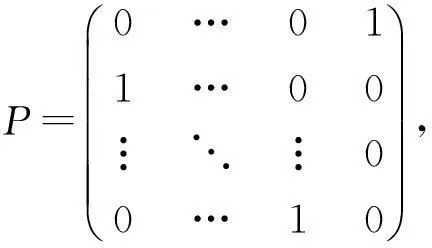
定义1设P为n阶基本置换因子循环矩阵，对于Mn中的矩阵πr如果满足

(1)

显然，πr的特征多项式和极小多项式都是xn-r.

定义2设πr∈PrCMn,对于Mn中的矩阵A,如果存在多项式

f(x)=a0+an-1x+an-2x2+…+a1xn-1，

称f(x)=a0+an-1x+an-2x2+…+a1xn-1为A的伴随多项式.

定义3[3]设矩阵A∈m×n，若存在矩阵B∈m×n及条件

(1)ABA=A，

(2)BAB=B，

(3)(AB)*=AB，

(4)(BA)*=BA，

(5)AB=BA，

则我们

称满足方程(1)～(4)的矩阵B为A的Moore-Penrose逆阵，并记为A+；

称满足条件(1)、(2)的矩阵B为A的反射g逆；

若满足方程(1)、(2)且其非零特征值是A的非零特征值的倒数的矩阵B为A的谱逆，记为As；

称满足条件(1)、(2)、(5)的矩阵B为A的群逆，记为A[1,2,5]或记为A#.

引理1[1]设Z是一个有不同特征值的n×n矩阵，φz表示所有与Z可交换的矩阵组成的集合，则φz中每一个矩阵A都有指标1，并且A的唯一谱逆As是A在φz中仅有的广义逆.

f(x)u(x)+g(x)v(x)=d(x).

引理3[4]一个非零矩阵A有唯一谱逆As当且仅当有指标1，这时As也是A的群逆A#.

2主要结果

定理1若设πr为满足(1)式的n阶第二类r-置换因子循环矩阵，对于Mn中的矩阵A，若A∈PrCMn，则πrA=Aπr.

证明因为A∈PrCMn,所以

则有

=Aπr.

定理1得证.

定理2设A∈PrCMn是奇异的，则A#=As.

由引理1和引理3以及定理1很容易得到定理2的证明，此处省略.

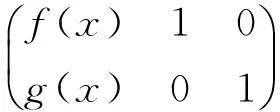
(1)若d(x)=1，则A可逆，并且A-1=u(πr)∈PrCMn.

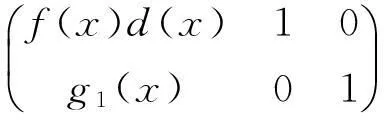
A#=As=d(πr)u1(Pr)且A#∈PrCMn.

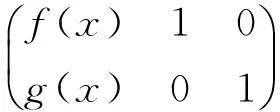
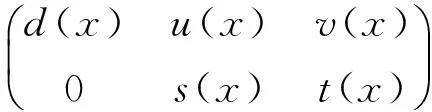
(1)若d(x)=1，由引理1，得到u(x)f(x)+v(x)g(x)=1，取x=πr，则由于f(πr)=A,g(πr)=0，所以Au(πr)=In，故A可逆，并且u(πr)是A的唯一逆矩阵，即A-1=u(πr)∈PrCMn.

(2) 若d(x)≠1，设f(x)=d(x)f1(x),g(x)=d(x)g1(x)，则(f1(x),g1(x))=1.由(d(x),g1(x))=1，得

(f(x),g1(x))=(d(x)f1(x),g1(x))=1.

又由(d(x),g1(x))=1,从而得

(f(x)d(x),g1(x))=1.

f(x)d(x)u1(x)+g1(x)v1(x)=1.

(1)

在(1)式两端右乘以h(x)，得

f(x)d(x)u1(x)f(x)+g1(x)v1(x)f(x)=f(x).

(2)

在(2)式中令x=πr，由于f(πr)=A,g(πr)=0，所以有

Ad(πr)u1(πr)A=A.

(3)

同理在(1)式两端左乘以d(x)u1(x)，并令x=πr，得

d(πr)u1(πr)Ad(πr)u1(πr)=d(πr)u1(πr).

(4)

又因为h(x)d(x)u1(x)=d(x)u1(x)h(x)，并令x=πr，得

h(πr)d(πr)u1(πr)=d(πr)u1(πr)h(πr)，

即有

Ad(πr)u1(πr)=d(πr)u1(πr)A.

(5)

由(3)、(4)、(5)及定义1知A#=d(πr)u1(πr).

下面给出的是通过定理1得到求第二类r-置换因子循环矩阵的逆和广义逆的一般步骤：

(1)由循环矩阵A∈PrCMn，找出πr，得到两个多项式f(x),g(x).

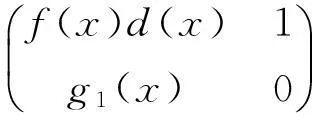
As=A#=d(πr)u1(πr).

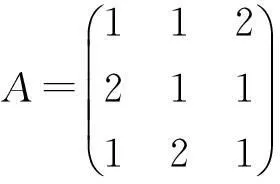
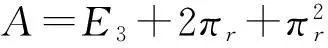
并且

f(x)=1+2x+x2，g(x)=x3-1.

显然d(x)=1.构造多项式矩阵

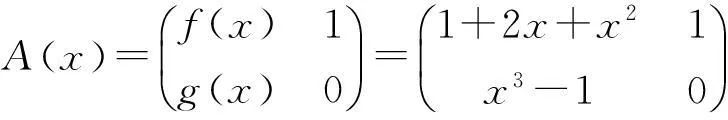
对A(x)只进行初等行变换：

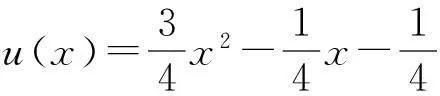
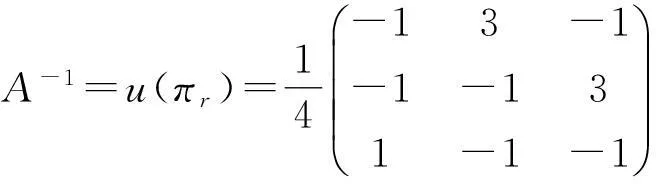
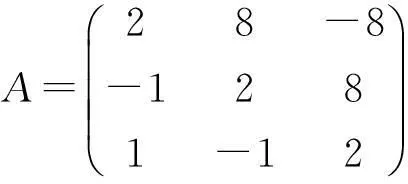
对A(x)只进行初等行变换：

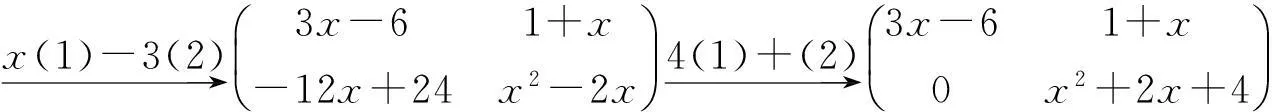
可以得出d(x)=x-2，这时

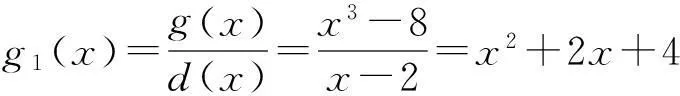
再构造多项式矩阵

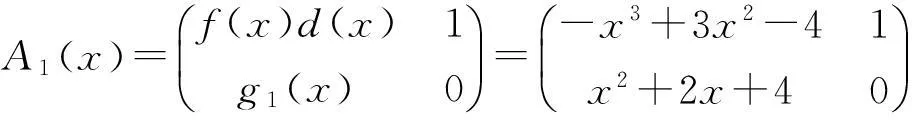
对A1(x)只进行初等行变换;

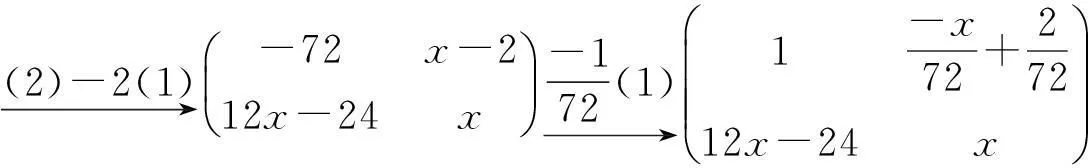
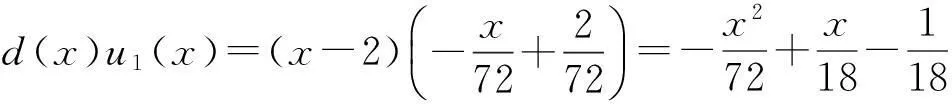
所以

参考文献：

[1]Cliue,R.E,Plemmons,R.J.andWorm,G..GeneralizedinversesofToeplitzmatrix[J].LinearAlgebraandItsAppl,1974, 8:25-33.

[2]张小红，蔡秉衡.高等代数专题研究选编[M].西安：西安科学技术出版社，1990.

[3]王国荣.矩阵与算子广义逆[M]. 北京：科学出版社，1998:1-3.

[4]ScroggsJE,OdellPL.Analternatedefinitionofapseudo-inverseofamatrix[J].JSocIndandApplMath,1966, 14:796-810.

[5]赵立宽,李振,孟令霞.关于第二类循环矩阵的几个性质[J].曲阜师范大学学报：自然科学版,2009,35(4):34-36.

[6]蒋加清.关于第二类循环矩阵求逆的一种算法[J].数学理论与应用,2012,32(1):87-90.

[7]胡艳,秦克云,孙继忠.r-块置换因子循环矩阵及其逆矩阵的求法[J].重庆师范大学学报：自然科学版，2012，29(4)：63-67.

[8]毛纲源.循环矩阵及其在分子振动中的应用[M].武汉:华中理工大学出版社,1995.

The Inverse and Generalized Inverse of the

Second Kind ofr-permutation Factor Circulant Matrix

HU Yan

(DepartmentofBasicCourses,Xi'anPeihuaUniversity,Xi’an710125,China)

Key words:the second kind of r-permutation factor circulant matrix; the second kind of r-permutation factor circulant matrix inverse; generalized inverse

责任编辑：周伦

中图分类号：O151.21

文献标识码：A

文章编号：1671-9824(2015)02-0010-05

作者简介：胡艳(1984—)，女，河南驻马店人，助教，硕士，研究方向：应用数学.

基金项目：西安培华学院校级科研项目(NO.PHKT20130609)

收稿日期：2014-12-21