基于HECC的门限群签密研究*

冯 阳，汪学明

(1.贵州大学 大数据与信息工程学院 ，贵州 贵阳 550025；2.贵州大学 计算机科学与技术学院 贵州 贵阳 550025)



基于HECC的门限群签密研究*

冯 阳1，汪学明2

(1.贵州大学 大数据与信息工程学院 ，贵州 贵阳 550025；2.贵州大学 计算机科学与技术学院 贵州 贵阳 550025)

分析了已有的门限群签密方案，针对现有方案中抗合谋攻击及身份追查等不足的问题，在(t,n)门限签密的基础上，基于HECC提出了一种可抗合谋攻击、身份可追查的高安全性门限群签密方案。该方案在可抵御合谋攻击的同时，可分辨攻击是来自于群成员还是外部，并可针对群成员的欺诈行为进行身份追查。该方案的安全性是建立在超椭圆曲线离散对数问题的难解性上，在保障安全的同时，也具备了HECC的诸多优点。

门限群签密；超椭圆曲线密码体制；合谋攻击；身份追查

0 引 言

1997年第一次提出“签密”概念[1]，指在一个合理的逻辑步骤中同时完成数字签名和信息加密两个步骤，其计算量和通信成本都要低于传统的“先签名后加密”[2]，在群体之间的网络通信过程中，门限群签密方案有着较高的安全性及可操作性，研究人员也提出了很多门限群签密方案。文献[3]首次提出了同时具备具备(t,n)签密和(k,l)解签密的门限群签密方案，之后文献[4]指出此方案有安全缺陷并进行了改进。针对文献[4]在群签密阶段计算效率较低的问题，文献[5]提出了新的签密方案，提高了计算效率。但在群签密组成员存在恶意欺诈行为时，上述方案都无法防范，而在解签密阶段，由于是先解密后验证，不能防止恶意信息的攻击，文献[6]针对上诉问题，提出了一种基于HECC的高安全性群签密方案，大大提高了群签密方案的安全性。

本文基于超椭圆曲线密码体制，针对上述方案中在抗合谋攻击以及对欺诈成员身份追查的不足，提出了一种新的改进方案，该方案在(t,n)门限群签密的基础上，受到攻击时可分辨该攻击是来自于群成员还是外部，并且可针对群成员的欺诈行为进行身份追查。该方案的安全性是建立在超椭圆曲线离散对数问题的难解性上，在保障安全的同时，也具备了HECC的诸多优点。

1 超椭圆曲线密码体制

超椭圆曲线密码体制是椭圆曲线密码体制的推广。Koblitz 在 1988 年提出了超椭圆曲线密码体制，其安全性基于有限域上超椭圆曲线的 Jacobian 上的离散对数问题(HCDLP)的难解性。

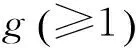
HECC作为ECC的推广，使其有ECC所不具备的优势，文献[9]中HP实验室在Pentium Pro334MHZ及NT平台下，使用Visual C++实现了ECDSA和HECDSA(超椭圆曲线数字签名)的对比分析；文献[10]中研究了ECC与RSA在同等安全强度下秘钥大小的具体函数表达，从而间接证明了HECC综合安全性更好。所以HECC较ECC具有以下优点：第一，ECC是亏格为1的超椭圆曲线，而在定义域相同的情况下，亏格越大曲线越多，意味着可用于选取的安全曲线越多，具有更高的安全性；第二，如同已经被广泛应用的ECC一样，可以模拟基于乘法群上如RSA、Elgamal等几乎所有协议；第三，安全水平相同时，HECC可选取更小的基域，而基域相同时，意味着HECC有更高的安全性，使HECC具有更高的研究价值。本文方案中如果选取亏格为3基域为60 bit，则与基域为180 bit的ECC安全性相同，远大于1 024 bit的RSA。

2 基于HECC的门限群签密方案

本方案基于HECC提出了一种可抗合谋攻击、身份可追查的高安全性门限群签密方案，方案有以下四部分组成：初始化、门限群签密生成、群签密验证和解签密阶段。

2.1 初始化阶段

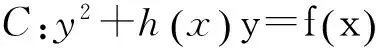
设有秘钥分发中心KDC(可为不可信分发中心)负责该阶段分配签密成员秘钥。秘钥分配过程如下：

(1)KDC随机选取s∈Zq为签密组私钥。签密组公钥Ds=s·D.

(2)利用Shamir的(t,n)门限方案[7], 随机选择ai(i=1,2,…,t-1)，利用拉格朗日插值定理构造t-1次多项式：

fs(x)=s+a1x+…+at-1xt-1∈Zq[x]

(1)

(3)设现有哈希函数(HashFunction)记为H，KDC计算所需公布信息：签密组成员公钥Dsi以及Dai。

Dsi=si·D Dai=ai·D

(2)

(4)利用Pedersen提出的一个可验证秘密分享方案VSS[8]，对KDC分发给签密组的秘钥进行验证。

(3)

由于现实情况中完全可信的分发中心几乎不存在，本方案通过上面两组验证可对分发中心KDC进行验证，防范了KDC的欺诈行为，所以该方案中KDC可以是不可信的。

2.2 门限群签密生成

2.2.1 成员签密生成

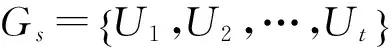
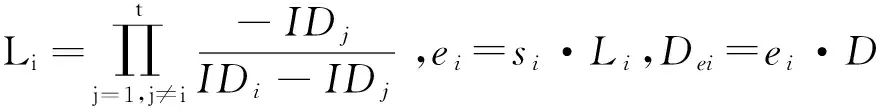
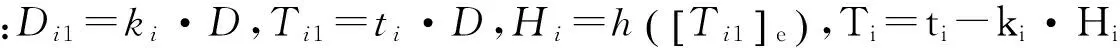
所有成员Ui收到其他成员Uj(i≠j)的广播信息后，为防范签密组成员间欺诈行为，通过下式对信息进行验证：

(4)

在所有Ui对广播信息进行验证通过后，计算:

(5)

2.2.2 群签密生成

KDC收到Si后，通过下式验证成员个体签名的有效性：

Si·D=R·Dei+Di1

(6)

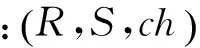
S·D=R·Ds+D1

(7)

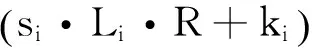
(8)

又由Largrange插值多项式可知：

(9)

综合以上可以得出：

S·D=s·D·R+D1=Ds·R+D1

(10)

2.3 群签密验证

(11)

因为如果签密组成员个人签名都通过验证是有效的且KDC和成员也通过S·D=R·Ds+D1验证，则可通过上式验证证明群签密的有效性，因为：

(12)

2.4 解签密阶段

通过上述一系列验证之后，解签密组成员通过下式恢复出秘密值m：

(13)

3 方案安全性分析

该方案是基于有限域上超椭圆曲线的Jacobian上的离散对数问题的难解性和(t,n)门限签名的安全性。目前,对于一般的低亏格(g<4)的超椭圆曲线离散对数问题的攻击都是指数时间的，所以本方案在计算上是安全的。方案利用Largrange门限方法实现方案的门限性，并通过一系列安全验证保证方案的安全性，如秘密分发时对KDC的验证、签密组成员间验证、群签密生成时对个人签名及KDC合成者的验证等。

3.1 方案门限性分析

本文方案在秘钥分配阶段利用拉格朗日插值多项式构造t-1次多项式：

(14)

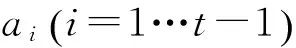
(15)

其行列式为：

(16)

由范德蒙行列式性质可知IDi互不相等，则含有t-1个未知数的t个线性方程组可以解出t-1个未知数s,a1,…,at-1，可以看出少于t个参与者无法求解。

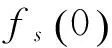
(17)

3.2 秘钥分配阶段的可验证性

利用Pedersen可验证秘密分享方案VSS[7]来验证KDC分发给成员的秘钥：

(18)

3.3 签密成员间个人签密的可验证性

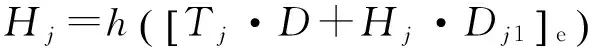
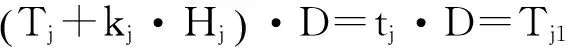
(19)

3.4 对群签密合成者的可验证性

群签密生成阶段，KDC对收到的个人签密进行验证：Si·D=R·Dei+Di1，验证通过说明个人签密的有效性，之后解签密人可利用S·D=R·Ds+D1对KDC进行验证，以确保KDC无欺诈行为，因为：

(20)

所以S·D=s·D·R+D1=Ds·R+D1同时通过上述验证可判断在遭受攻击时，攻击是否来自外部。

3.5 验证的匿名性和身份可追查性

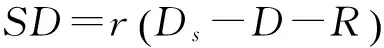
4 结束语

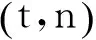
[1]ZHENGYU-liang.DigitalSigncryptionorHowtoAchievecost(Signature&Encryption)<

[2] 雷咏,杨世平. 基于PKI的签密体制[J]. 通信技术,2013,46(1):43-46. LEI Yong, YANG Shi-ping. Signcryption System based on PKI[J] Communications Technology, 2013,46(1):43-46.

[3] WANG C T,CHANG C C,LIN C H. Generalization ofThreshold Signature and Authenticated Encryption for Group Communications[J]. IEICE Transactions on Fundamentals, 2000, E83-A (6): 1228-1237.

[4] Hsu C L,Wu T S,Wu T C. Improvements ofGeneralization of Threshold Signature and Authenticated Encryption for Group Communications[J]. Information Processing Letters. 2002, 81(1):41-45.

[5] 彭长根,李祥,罗文俊. 一种面向群组通信的通用门限签密方案[J]. 电子学报,2007,01:64-67. PENG Chang-gen, LI Xiang, LUO Wen-jun. A Generalized Group-Oriented Threshold Signcryption Schemes[J]. Electronic journals, 2007,01:64-67.

[6] 冯君,汪学明. 一种高安全的门限群签密方案[J]. 计算机应用研究,2013,02:503-506. FENG Jun,WANG Xue-ming.Threshold group signcryption scheme with high security[J]. Computer application research, 2013,02:503-506.

[7] Sharmir A.How to Share a Secret [J]. Communication of the ACM, 1979, 22(11):612-6130.

[8] Pedersen T P.Distributed Provers with Applications to Undeniable Signatures. [C]//Eurocrypt'91,Lecture Notes in Computer Science 547 .New York: Springer-Verlag,1991.221-238.

[9] Solinas J. Efficient Arithmetic on Koblitz Curves [J], Designes, Codes and Cryptography 19(2000),195-249.

[10] Blake I，Seroussi G, Smart N. Elliptic Curves in Cryptography [J]. Cambridge: University Press,1999.

Threshold Group Signcryption based on HECC

FENG Yang1, WANG Xue-ming*2

(1.College of Big Data and Information Engineering, Guizhou University , Guiyang Guizhou 550025,China；2.College of Computer Science and Technology, Guizhou University, Guiyang Guizhou 550025,China)

This paper analyzes the existing threshold group signcryption schemes,and aiming at the problems of anti-conspiracy attack and limited identity-tracing and with (t, n) signcryption as the basis, proposes a more secure threshold group signcryption scheme based on HECC (Hyperelliptic Curve Cryptosystem). This scheme could effectively resist conspiracy and distinguish between external attacks and internal attacks, and meanwhile carry out identity-tracing in accordance with the fraudulent practice of group members. Scheme security relies on the difficult solution of discrete logarithm problem of hyperelliptic curve, and thus to guarantee security while enjoy many advantages of HECC.

threshold group signcryption; HECC; conspiracy attack; identity- tracing

10.3969/j.issn.1002-0802.2015.05.020

2015-01-05；

2015-04-20 Received date:2015-01-05；Revised date：2015-04-20

国家自然科学基金项目[2011]61163049；贵州省自然科学基金项目黔科合J字[2011]2197

Foundation Item:National natural science fund project[2011]61163049; Guizhou province natural science fund project[2011]2197

TP393

A

1002-0802(2015)05-0607-04

冯 阳(1986-)，男，硕士研究生，主要研究方向为密码学与信息安全；

汪学明(1965-)，男，博士，教授，主要研究方向为无线与移动通信、协议分析与模型检测、密码学与信息安全。