一种新的基于压缩感知的多焦点图象融合方法*

宋 斌，吴乐华，王 开，郭辉，岳 鑫

(重庆通信学院，重庆 400035)



一种新的基于压缩感知的多焦点图象融合方法*

宋 斌，吴乐华，王 开，郭辉，岳 鑫

(重庆通信学院，重庆 400035)

提出一种基于压缩感知和脉冲耦合神经网络的图像融合算法，包括三部分：图像傅里叶变换稀疏表示、测量融合和图像重构。首先，将双通道脉冲耦合神经网络(Dual-PCNN)模型应用到整个算法当中；其次，针对新的融合框架及傅里叶变换的系数特点，提出双星型采样下基于测量值标准差的加权融合方法；最后，通过最小全变分算法重构图像。实验仿真结果证明该方法优于其他基于傅立叶变换的方法。

压缩感知；图像融合；双通道脉冲神经网络；标准差

0 引 言

图像融合就是通过某种算法将不同传感器获取的同一个场景的多个成像信息融合为一幅新图像，融合后的图像具有比源图像更丰富、更精确的信息，更适合人类视觉及计算机检测、分类、识别、目标定位、情景感知等处理[1]。多焦点图像融合作为图像融合的一个重要分支，它可将多幅已经配准的、成像条件相同的同一场景的不同聚焦图像，融合成一幅更加清晰的图像。传统的图像融合算法主要是基于多尺度变换，如金字塔融合、离散小波变换融合等[2-4]。近几年，Johnson和Padgett[5]发现脉冲耦合神经网络(Pulse Coupled Neural Network, PCNN)可以有效运用于图像融合领域[6-8]。但是以上这些传统图像融合方法主要处理是其变换域数据或原始数据，要对每一个数据进行计算，需要得到原始图像的先验信息、较大的存储空间以及较高的计算复杂度。压缩感知(Compressive Sensing ,CS)理论表明，若信号是稀疏或可压缩的，则可用少量的非自适应线性测量值即可精确重构原始信号[9]。在图像融合处理中，CS的优势在于能有效减少存储空间和计算成本，且可不用获取被观察信号的任何先验信息。

本文结合PCNN图像融合算法及CS理论的特点，为了尽可能多的获取图像的细节信息提出一种新的基于压缩感知的图像融合算法，首先将双通道脉冲耦合神经网络(Dual-channel Pulse Coupled Neural Network, Dual-PCNN)模型作为一个重要组成部分应用到整个融合算法当中，并结合傅立叶稀疏变换的系数特点，采用双星型采样下基于测量值标准差(Standard Deviation,SD)的加权融合方法，实验证明该方法能够有效进行图像融合，并获得较好的融合质量。

1 压缩感知基本原理

设一个实值、有限长的一维离散信号x，可视为x{n}∈RN中的一个N×1列向量(n=1, 2, …,N)。若信号x可表示为：

x=Ψα

(1)

其中，Ψ是N×N基向量矩阵，若α只包含K个非零向量，则称x是K稀疏[9]。

通过y=Φx得到压缩测量值，其中y∈RM，Φ是M×N测量矩阵，可得：

y=ΦΨα=Θα

(2)

虽然从M

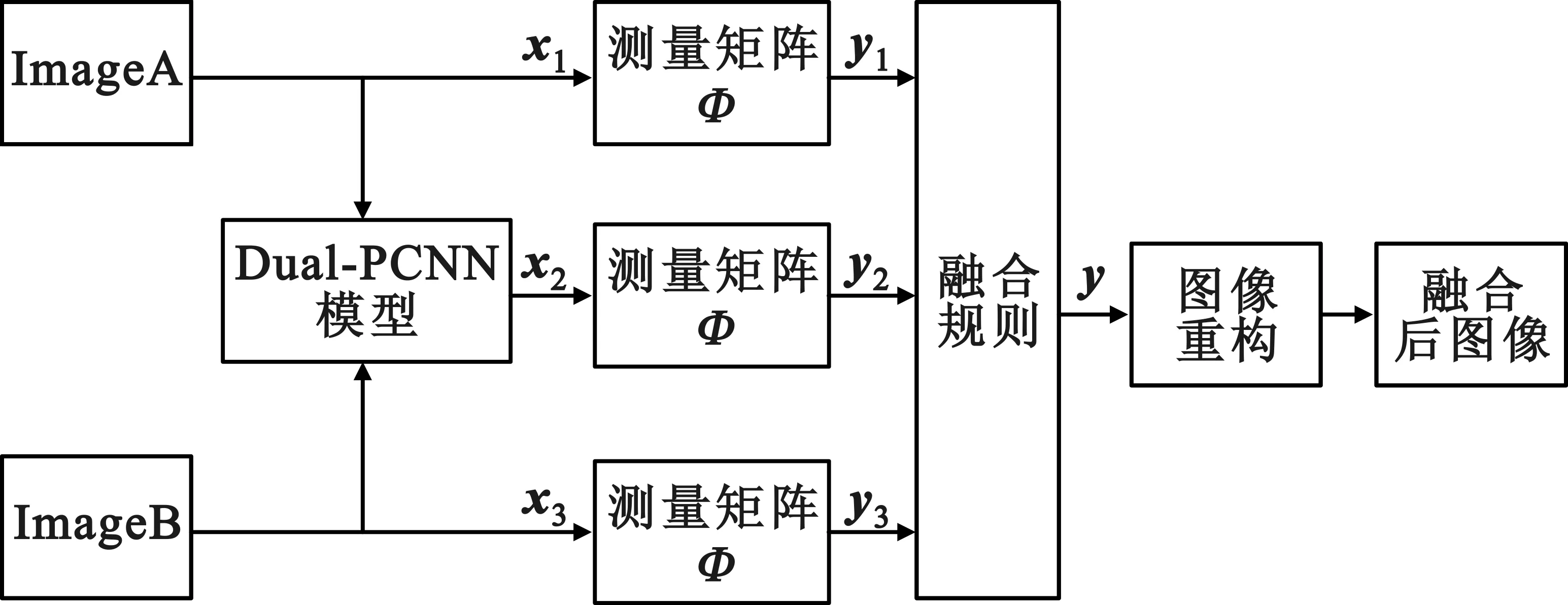
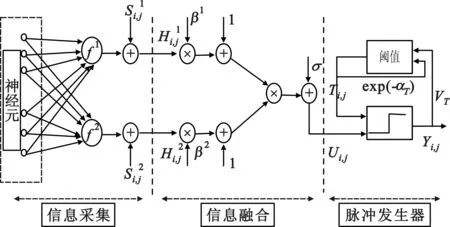
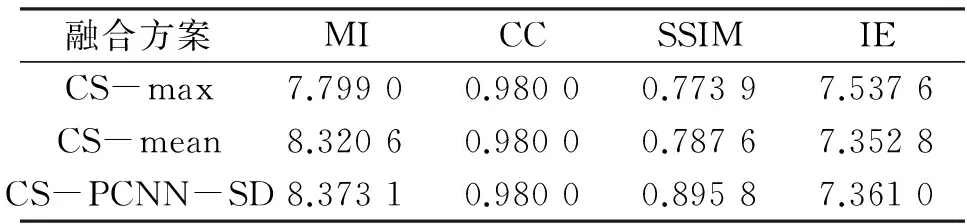
2 一种新性的基于压缩感知的图像融合

本文的图像融合框架如图1所示，为了从原图像中获得更加丰富的细节信息，将Dual-PCNN模型有效应用到整个融合框架中。其中，x1、x2是原图像A、B经过傅里叶变换后的稀疏信号，x3是原图像A、B在Dual-PCNN模型作用下再经过傅里叶变换后的稀疏信号；y1、y2、y3分别为稀疏信号x1、x2、x3经过同一测量矩阵Φ测量后的值，使用基于SD的加权平均融合规则对y1、y2、y3进行融合得到y，然后更适合二维图像重构的全最小全变分(Total Variation, TV)法[10-11]，重构得到融合后的图像。

图1 图像融合框架

2.1 Dual-PCNN模型

Dual-PCNN是PCNN的改进模型，克服了单通道PCNN的不足之处，能有效实现对多幅图像的同时融合[12]。Dual-PCNN模型如图2所示，主要由三部分组成：信息采集、信息融合和脉冲发生器。信息采集部份能够接收来自神经元的两个以上的信息触发；信息融合部分主要进行待融合图像信息的融合；脉冲发生器则负责产生对信息采集单元的触发脉冲。

若把图像中某像素的坐标记为(i,j)，则Dual-PCNN模型可详细描述如下：

(3)

(4)

(5)

(6)

Ti,j[n]=exp(-αT)Ti,j[n-1]+VTYi,j[n]

(7)

图2 Dual-PCNN模型

本文通过实验选取参数σ=1，Ti,j为与图像输入大小相同，元素大小为500的单位矩阵，αT、VT分别选择0.012、3 000，迭代次数n为10。

2.2 采样模式

采样矩阵的设计将直接影响图像重构的质量，由于图像经过FFT变换后，其低频信息集中在频率坐标系的中间，而图像的信息主要体现在低频信息中。本文针对图像傅立叶变换系数的这一特点采用文献[13]中提出在低频区域得到更高密度采样的双星采样模式，如图3所示。同时文献[13]证明采用双星采样模式图像的重构质量更好，且计算时间更少。

图3 双星采样矩阵

2.3 基于测量值标准差的加权融合

文献[13]基于CS的融合算法是对测量值取绝对值最大，文献[14]是对测量值取算术平均。针对上述融合算法，本文结合新的CS融合框架提出基于测量值标准差的加权融合方法，该算法大大改进了文献[13]和文献[14]的融合效果。

具体实现流程是：输入：Image A ,Image B;输出：融合后图像D。

(1)将图像A、B和经过Dual-PCNN的信号C进行傅里叶变换并分别向量化：

A=(a1,a2,…,aN)T

(8)

B=(b1,b2,…,bN)T

(9)

C=(c1,c2,…,cN)T

(10)

(2)对傅里叶变换后的系数通过双星型采样模式构造M×N的测量矩阵Φ；

(3)计算A、B、C的测量值：

X=(x1,x2,…,xM)T=ΦA

(11)

Y=(y1,y2,…,yM)T=ΦB

(12)

Z=(z1,z2,…,zM)T=ΦC

(13)

(4)计算标准差sdx、sdy和sdz；

(5)根据标准差计算相应的加权因子：

ω1=sdx/(sdx+sdy+sdz)

(14)

ω2=sdy/(sdx+sdy+sdz)

(15)

ω3=sdz/(sdx+sdy+sdz)

(16)

(6)计算融合后的测量值F=(f1,f2,…,fM)T：

F=ω1×X+ω2×Y+ω3×Z

(17)

(7)利用F通过最小全变分方法重构融合图像F′：

MinTV(F′)Subject to‖ΦF′-F‖2≤ε

(18)

( 8)将F′进行傅里叶逆变换得到融合后图像D。

3 仿真结果及分析

图4 clock A、clock B及Dual-PCNN融合图

图5 不同融合方法的融合图像

从主观视觉效果上评价，CS-max融合方法得到的融合图像有明显的条纹现象，CS-mean及CS-PCNN-SD融合方法均能够在有效抑制条纹现像，但是CS-PCNN-SD融合方法相对于CS-mean融合方法得到的融合图像亮度分布更加均匀，显示更加理想的视觉图像。

在客观评价方面，本文从互信息(mutual information, MI)[15]、相关系数(correlation coefficient, CC)[16]以及结构相似度(structural similarity, SSIM)[17]、熵(Information Entropy，IE)四个客观评价参数进行评价。互信息越大，说明从原图像中获得的信息越多，图像融合效果越好；相关系数越接近1，说明图像融合越好；结构相似度和熵越大，说明图像的融合效果越好。四个评价参数的统计结果如表1所示。

表1 各融合方案的评价参数统计

从表1对评价参数的统计可知，三种融合方案的相关系数(CC)都非常接近1。在信息熵方面，由于CS-max融合算法带入较多噪声值较大，对于MI、SSIM、IE三个客观评价标准而言，新的融合框架加入了Dual-PCNN模型，并结合新的融合框架特点，采用基于测量值标准差的加权融合方法，极大丰富了采样值的信息来源，CS-PCNN-SD融合算法所得值明显大于CS-max融合算法和CS-mean融合算法所得值，因此通过对客观评价标准参数的统计分析可知，本文的融合算法具有明显优势，并能得到效果更佳的融合图像。

4 结束语

本文研究了人工智能神经网络Dual-PCNN模型与压缩感知理论的结合，并成功应用到多焦点图像融合中，有效证明了人工智能神经网络与压缩感知理论相结合的可行性。通过与现有的FFT稀疏表示下压缩感知图像融合算法实验仿真及结果统计分析对比，证明本文的融合算法实现图像融合效果更好，同时也为进一步研究基于CS的图像融合提供了参考。由于人工智能神经网络参数较多，下一步将重点研究参数选择对整个算法的影响。

[1] WANG Z, ZOU D,Armenakis C, et al. A comparative Analysis of Image Fusion Methods[J]. Geoscience and Remote Sensing, IEEE Transactions on, 2005, 43(6): 1391-1402.

[2] 李小娟, 赵巍. 一种基于多尺度边缘的图像融合算法[J]. 北京航空航天大学学报,2007,33(2):229-232. LI Xiao-juan, ZHAO Wei. A Novel Image Algorithm based on Multiscale Edge Fusion[J]. Journal of Beihang University, 2007, 33 (2): 229-232.

[3] 方辉，尹忠科.一种基于NSCT的区域能量图像融合算法[J].通信技术，2010, 43 (03):137-141. FANG Hui, YIN Zhong-ke. A Fusion Algorithm of Regional Energy Image based on NSCT[J]. Communications Technology, 2010, 43 (03): 137-141.

[4] 李国新. 基于Ridgelet变换的图像融合[J]. 通信技术, 2009, 42 (06): 144-146. LIGuo-xin. The Image Fusion based on Ridgelet Transform.[J]. Communication Technology,2009, 42 (06): 144-146.

[5] Johnson J L, Padgett M L. PCNN Models andApplications[J]. IEEE Transactions on Neural Networks/a publication of the IEEE Neural Networks Council, 1998, 10(3): 480-498.

[6] CHAI Y, LI H F, QU J F. Image Fusion Scheme Using a Novel Dual-Channel PCNN in Lifting Stationary WaveletDomain[J]. Optics Communications, 2010, 283(19): 3591-3602.

[7] WANG Z, MA Y, GU J. Multi-Focus Image Fusion UsingPCNN[J]. Pattern Recognition, 2010, 43(6):2003-2016.

[8] KONG WW, LEI Y J, LEI Y, et al. Image Fusion Technique based on Non-Subsampled Contourlet Transform and Adaptive Unit-Fast-Linking Pulse-Coupled Neural Network[J]. Image Processing, IET, 2011,5(2):113-121.

[9] Donoho D L. Compressed Sensing [J]. Information Theory, IEEE Transactions on, 2006, 52(4): 1289-1306.

[10] Candès E J, Romberg J, TAO T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information[J]. Information Theory, IEEE Transactions on, 2006, 52(2): 489-509.

[11] Schmidt M, Fung G, Rosales R. Fast Optimization Methods for l1 Regularization: A Comparative Study and Two NewApproaches[M]//Machine Learning: ECML 2007. Springer Berlin Heidelberg, 2007:286-297.

[12] WANG Z, MA Y. Medical Image Fusion Using m-PCNN[J]. Information Fusion, 2008, 9(2): 176-185.

[13] Wan T, Qin Z. An Application of Compressive Sensing for ImageFusion[J]. International Journal of Computer Mathematics, 2011, 88(18): 3915-3930.

[14] LI X, QIN S Y. Efficient Fusion for Infrared and Visible Images based on Compressive Sensing Principle [J]. IET Image Process, 2011, 5 (02): 141-147.

[15] Xydeas C S, Petrovic V. Objective Image Fusion Performance Measure[J]. Electronics Letters, 2000, 36(4): 308-309.

[16] Yang S,Gao J. Seismic Quality Factors Estimation from Spectral Correlation[J]. Geoscience and Remote Sensing Letters, IEEE, 2008, 5(4): 740-744.

[17] WANG Z,Bovik A C, Sheikh H R, et al. Image Quality Assessment: from Error Visibility to Structural Similarity[J]. Image Processing, IEEE Transactions on, 2004, 13(4): 600-612.

A Novel Multi-focus Image Fusion Algorithm based on Compressive Sensing

SONG Bin, WU Le-hua, WANG Kai, GUO Hui, YUE Xing

(Chongqing Communication Institute, Chongqing 400035, China)

A novel multi-focus image fusion algorithm based on compressive sensing and the pulse-coupled neural network is proposed, this algorithm consists of three parts: image Fourier transform sparse representation, measurement fusion and image reconstruction. Firstly, the Dual-PCNN (Dual-Channel Pulse Coupled Neural Network) model is applied in the whole algorithm. Then, aiming at coefficient characteristics ofthe novel fusion frame and the Fourier transform, weight fusion method based on standard deviation of the measured values under the double star sample is proposed. Finally, the fused image is reconstructed by Total Variation algorithm. Experiment simulation results indicate that the proposed algorithm is superior to other existing Fourier transform algorithms.

compressive sensing; image fusion; Dual-PCNN; standard deviation

10.3969/j.issn.1002-0802.2015.05.009

2015-01-27；

2015-04-02 Received date:2015-01-27；Revised date：2015-04-02

重庆市自然科学基金(No.cstc2013jcyjA40045);重庆市自然科学基金(No.KJTD201343)Foundation Item:Chongqing Natural Science Foundation(No.cstc2013jcyjA40045)；Chongqing Natural Science Foundation(No.KJTD201343)

TP391

A

1002-0802(2015)05-0551-04

宋 斌(1984—)，男，硕士研究生，主要研究方向为图像处理；

吴乐华(1965—)，女，硕士，教授，主要研究方向为图像处理；

王 开(1983—)，男，硕士，讲师，主要研究方向为信号处理；

郭 辉(1982—)，男，硕士研究生，主要研究方向为信息安全；

岳 鑫(1990—)，男，硕士研究生，主要研究方向为信息安全。