基于改进TOPSIS-DEA模型的采油厂绩效评估方法

刘 岩 罗东坤 魏新强 张宝生.中国石油大学(北京)工商管理学院, 北京 049；.中国石油集团经济技术研究院, 北京 00



基于改进TOPSIS-DEA模型的采油厂绩效评估方法

刘 岩1罗东坤1魏新强2张宝生1
1.中国石油大学(北京)工商管理学院, 北京 102249；2.中国石油集团经济技术研究院, 北京 102220

传统的数据包络分析(DEA)方法应用于绩效评估无法体现决策者的决策偏好,也无法对有效评价单元进行全排序。在考虑偏好的前提下,运用主观评价方法构造DEA偏好矩阵；以理想点排序(TOPSIS)原理为基础,通过虚拟最优和最差前沿面的方式构造正理想点和负理想点,并以相对贴近度指数计算各评价单元的DEA全排序值。采用12家采油厂的数据进行实例分析,分别以油气生产、安全生产和环保生产为优先条件进行绩效评估,结果显示改进TOPSIS-DEA模型方法在采油厂绩效评估优选中有实用意义。

绩效评估；数据包络分析；理想点排序；偏好矩阵

0 前言

数据包络分析(DEA)方法广泛应用于绩效评估领域中,但传统DEA方法在绩效评估中存在无法体现决策者的决策偏好[1-2]和无法对有效评价单元进行全排序的问题[3-4],影响了该方法的应用效果。针对DEA方法在绩效评估过程中的不足,结合现有的方法理论提出改进措施：针对DEA指标权重与绩效评估指标主观感受不符的问题,将偏好锥理论引入绩效评估过程,根据指标层次、指标间的重要性,制定相应的偏好方程加入DEA模型,使主观权重体现在DEA运算排序过程中；针对DEA模型不能对有效单元进行全排序的问题,采用构造最优和最差虚拟前沿面的方法进行有效性单元的非有效化,然后以理想点排序(TOPSIS)原理进行有效单元排序,并以此作为采油厂绩效评估方法。

1 基于TOPSIS的绩效评估DEA模型

针对传统企业绩效评估在偏好和全排序两方面的不足,分别采用偏好矩阵和TOPSIS 原理进行改进。

1.1 DEA权重与主观认识相结合

主观定量化的方法包括层次分析(AHP)、模糊综合评价等方法,与DEA权重相结合的主要原理是将权重的主观认识定量化,并作为相对应的约束要求加入DEA评价模型中,表达式为：

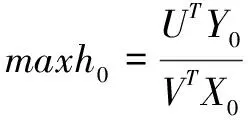
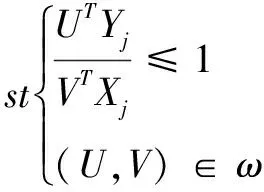
(1)

式中：ω为权重的主观定量化矩阵；Y为产出指标数值矩阵；U为产出指标权重矩阵；X为投入指标数值矩阵；V为投入指标权重矩阵。

1.2DEA评价单元的全排序

对于DEA有效单元的排序,经过拓展DEA方法和理论,已有多种处理方法,如交叉DEA模型、超效率DEA模型、BENCHMARK-DEA模型、DEA模型与数学统计方法相结合,以及DEA模型与其他决策方法相结合等方法。这些方法均以传统模型为应用基础,以被评价的决策单元投入产出数据与生产能力最优单元组成的前沿面进行比较,是基于最优前沿面进行计算的。这些方法在效率评价领域应用中完全符合要求,效率好坏是由被评价单元与最优生产实践水平的距离决定。但当这些方法用于排序功能时,其结果往往具有一定局限性,因在排序过程中,仅考虑了评价单元最优,而没有考虑不利于评价单元。为此,杨峰等人[5]将最优前沿面和最差前沿面结合成完全包络面,并借鉴超效率DEA的思想,提出一种新的DEA排序方法,但该方法数据属非线性范畴,求解过程相对困难。考虑各DEA方法的优缺点,借鉴卞亦文等人[6]的建模思路,在排序方面将虚拟完全包络面和TOPSIS原理相结合进行DEA各评价单元的全排序。其中,虚拟包络面包括虚拟最优前沿面和虚拟最差前沿面,构造原理见图1。以最优前沿面为例,假定DEA模型所形成的前沿面为ABCDE,则传统DEA模型中,A、B、C、D、E这五点均处于前沿面上,其效率值均为1,不可进行区分,为了能够区分这些有效的评价单元,可以通过虚拟单元的设定,以原始的有效单元数据为基础,缩小其单位产出所消耗的投入数据,构造出一个新的前沿面PQRST,使原有的有效单元变为非有效单元,进而对这些单元进行评价。对于集成排序方面,为实现有效单元的评价,借鉴逼近理想点排序,在DEA模型的最优前沿面中选取最有效的正理想点,从最差前沿面中选取最差的负理想点,同时考虑评价单元与正理想点和负理想点之间的关系建立TOPSIS效率评估指数,以此为标准建立各决策单元的排序，下面阐述了DEA方法的改进步骤。

步骤1：设定DEA模型的权重主观偏好。通过AHP或模糊综合评价或偏好序方法进行DEA模型的权重偏好设定。

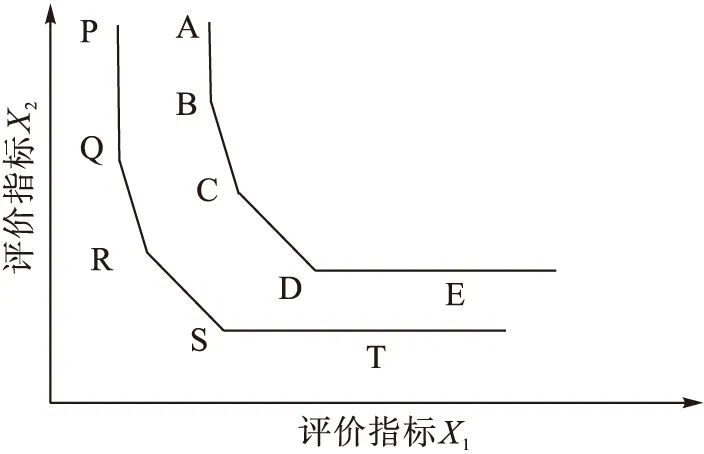
图1 虚拟前沿面的构建思路图

步骤2：区分评价单元的有效与非有效。运用设置偏好锥的DEA模型求解各评价单元的效率值,区分有效单元与非有效单元。

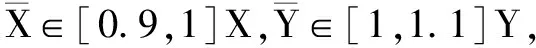
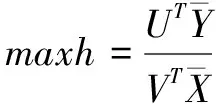
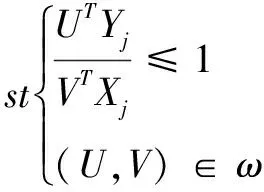
(2)

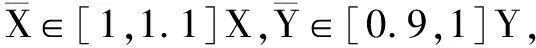
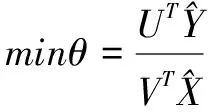
(3)

步骤5：构造正理想点与负理想点。针对构造的最优虚拟评价单元,设定(xa,ya)为最优虚拟单元中的正理想点,其中,xa=min{X},ya=max{Y}；设定(xb,yb)为最差虚拟单元中的负理想点,则xb=max{X},yb=min{Y}；将正、负理想点分别带入基于最优、最差前沿面的DEA模型中,求得正、负理想点的效率值,分别用ha和θb表示[8]。

步骤6：基于TOPSIS原理的排序思想,构建排序指数。以虚拟的最优、最差前沿面为评价标准面,计算各评价单元与正负理想点之间的距离,依据相对贴近度的原理进行各评价单元的排序,相对贴近度排序指数：

(4)

式中：C为相对贴近度排序指数；θi为以最差虚拟前沿面为标准计算出的第i个评价单元的效率值；hi为以最优虚拟前沿面为标准计算出的第i个评价单元的效率值。

2 采油厂绩效评估基础信息处理

2.1 采油厂基本情况

D公司是以油气勘探开发和油气深加工为经营业务的油田公司,下属47个二级单位,二级单位中含12个采油厂,本文以12个采油厂作为评价单元,进行TOPSIS-DEA模型的实例研究。在指标选取方面,由于同级别、同类型石油企业在自身条件和所处发展阶段等方面不同,即使同样的指标值,所反映的不同企业的实力或绩效却不同。因此,指标要根据不同的条件进行调整才更合理。一般来说,公司的整体实力主要从公司现有生产状况、可持续发展前景、社会责任等方面来体现,因此,在公司层次进行绩效指标选取时,主要从以上三方面进行考虑。公司指标涉及成本效益、技术和综合管理三类,具体指标通过专家调查确定,各采油厂指标体系与基础数据见表1。

表1 各采油厂指标体系与基础数据

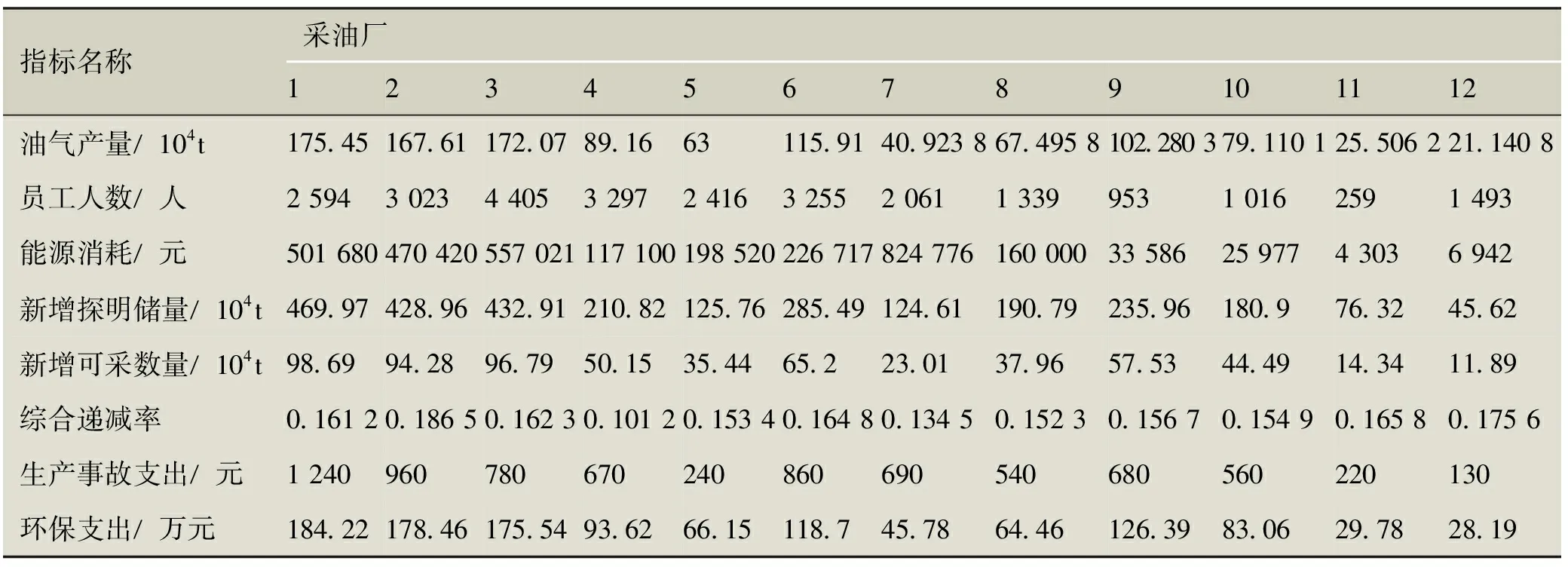
指标名称采油厂123456789101112油气产量/104t175 45167 61172 0789 1663115 9140 923867 4958102 280379 110125 506221 1408员工人数/人2594302344053297241632552061133995310162591493能源消耗/元501680470420557021117100198520226717824776160000335862597743036942新增探明储量/104t469 97428 96432 91210 82125 76285 49124 61190 79235 96180 976 3245 62新增可采数量/104t98 6994 2896 7950 1535 4465 223 0137 9657 5344 4914 3411 89综合递减率0 16120 18650 16230 10120 15340 16480 13450 15230 15670 15490 16580 1756生产事故支出/元1240960780670240860690540680560220130环保支出/万元184 22178 46175 5493 6266 15118 745 7864 46126 3983 0629 7828 19

2.2 绩效指标的调整

采油厂或油气生产作业区的作业效果在相当程度上受自然条件影响,因此,如果不对指标进行处理便进行绩效评估,其评价过程不客观,不能真实反映采油厂或油气生产作业区的管理状况及努力程度。因此,对某些综合指标需要进行调整,这些指标即为条件指标。本文涉及到的条件指标包括油气产量和综合递减率,这两个调整指标的相关因素见表2[9]。

表2 条件指标影响因素

条件指标影响因素油气产量渗透率生产压差孔隙度流动系数原油黏度有效厚度综合递减率已开采时间含水率采油速度

条件指标具体处理方法：以油气产量指标为例(表2),油气产量有6个影响因素,假设某油田公司有m个采油厂参与绩效考核,第i个采油厂油气产量的影响因素的实际数值分别是fi1,fi2,…,fi6。在这6个影响因素中,原油黏度fi5是逆向指标(越小越好),其余为正向指标(越大越好)。首先计算各影响因素条件指数kj，原油黏度fi5的条件指数ks=min{fij}/fis，其他指标的条件指数ki=fij/max{fij}。

设影响因素的权重分别为w1,w2,…,w6,则通过条件指数调整后的油气产量为：

(5)

式中：Q′为通过条件指数调整后的油气产量，104t；Q为实际油气产量，104t。

对于综合递减率指标,与油气产量不同,它属于逆向指标(越小越好),在进行条件指标处理时应注意不同之处。

在计算各影响因素条件指数方面,计算公式及处理过程与正向指标的处理方法相同,但在最后计算通过条件指数调整后的综合递减率时,则采用对应调整系数公式的倒数形式,见式(6)。

(6)

对12个采油厂的基础数据进行处理,涉及到的条件指标按照前面综合递减率的调整过程进行调整后,得到各采油厂相应的指标值,见表4。

表3 综合递减率调整结果表

标号实际综合递减率/()影响因素的条件指数与权重的乘积已开采时间/a含水率/()采油速度/()综合调整指数调整后综合递减率/()采油厂116 120 260 270 350 8814 18

表4 采油厂调整后指标值

指标名称采油厂123456789101112投入指标 油气单位综合成本/(元·t-1)600 78515 04733 5661 6757 211056 41569 5133995310162591493 油气单位操作成本/(元·t-1)269 15281 24336 25312 1389 58376 59464 63313 94338 62446 16226448 7 生产事故损失指数/(元·104t-1)7 065 7224 537 513 87 4116 8686 67 078 626 14 综合递减率/()14 1816 6417 329 6813 5614 5812 5615 2315 8916 2415 2817 8 环保支出指数/(元·t-1)1 041 061 021 051 051 021 110 951 231 041 161 3产出指标 全员效率/(t·人-1)0 060 050 030 020 020 030 010 050 10 070 090 01 油气当量条件调整指数1 130 981 041 140 940 851 120 891 070 840 961 04 新增探明储量指数2 672 552 512 361 992 463 042 822 32 282 992 15 新增可采储量指数0 520 490 460 480 360 430 540 460 380 460 580 41 节能效果指数/()6 242 546 454 783 423 282 345 675 896 673 452 56

3 采油厂绩效评估实例分析

指标体系中的投入指标可分为三类,一为油气生产类,油气单位综合成本、油气单位操作成本、综合递减率；二为安全生产类,生产事故损失；三为环保类,环保支出[10]。由于各采油厂采取的生产策略不同,以及生产过程的油气生产、安全和环保的偏好顺序不同,因此首先通过各权重的设置进行生产偏好的设置,然后通过TOPSIS-DEA模型进行求解,并将所得结果与传统DEA模型结果进行对比,见表5。

表5 TOPSIS-DEA模型与传统DEA模型对比结果

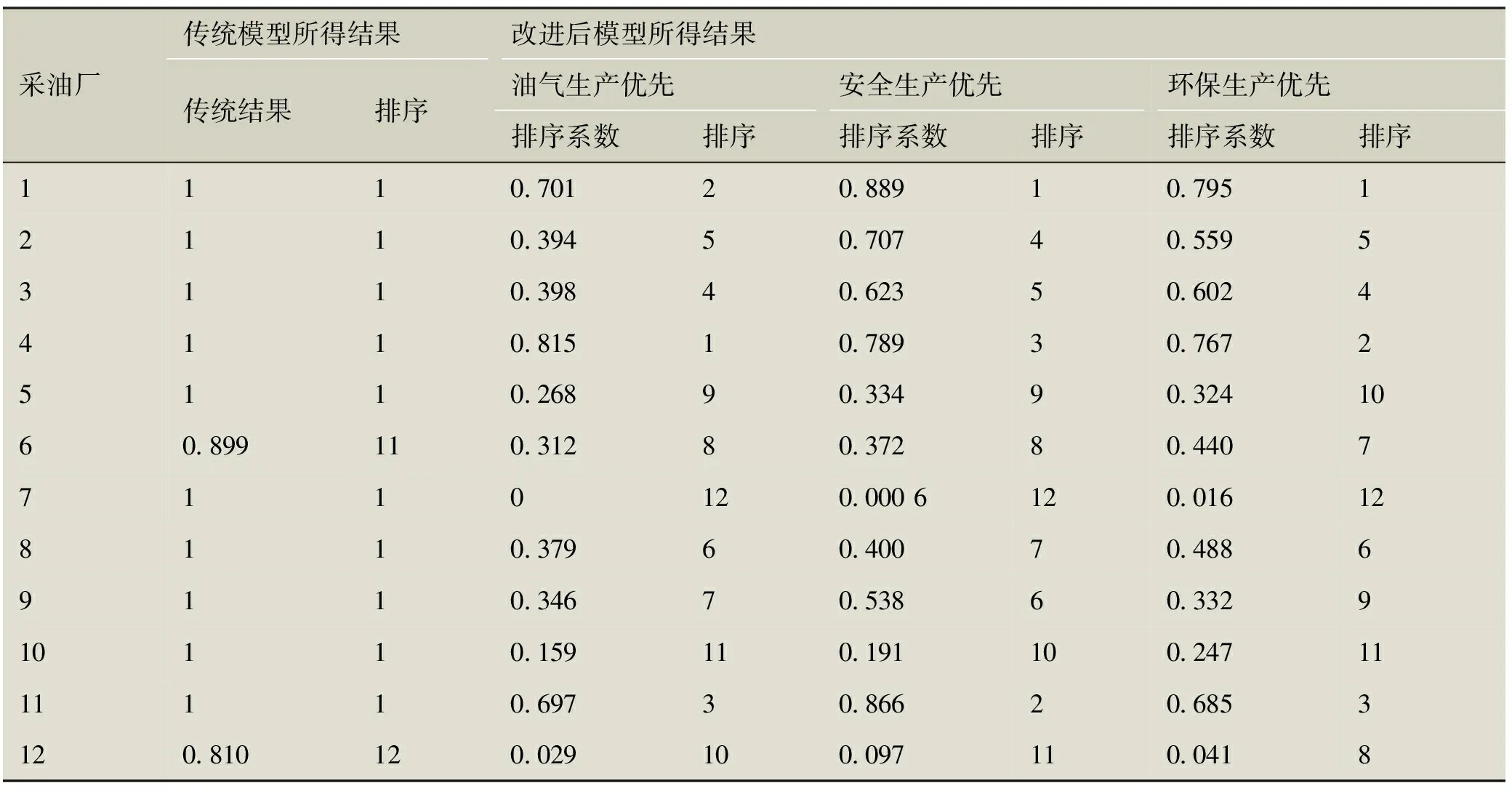
采油厂传统模型所得结果改进后模型所得结果传统结果排序油气生产优先安全生产优先环保生产优先排序系数排序排序系数排序排序系数排序1110 70120 88910 79512110 39450 70740 55953110 39840 62350 60244110 81510 78930 76725110 26890 33490 3241060 899110 31280 37280 44077110120 0006120 016128110 37960 40070 48869110 34670 53860 332910110 159110 191100 2471111110 69730 86620 6853120 810120 029100 097110 0418

由表5可看出,传统DEA模型因无法区分效率值为1的各评价单元而无法进行排序,TOPSIS-DEA改进模型却能得到很好的结果,因此,在现有的采油厂中,以油气生产优先分析,采油厂4的绩效排名最好,采油厂7绩效最差,排名第12位；以安全生产优先分析,采油厂1排名第1位,采油厂7排末尾；以环保生产优先分析,最优单元依然是采油厂1,最差单元同样是采油厂7,因此,无论依据哪种偏好进行排序,采油厂7都是最差单元。对比三种偏好情况下的结果发现,采油厂1、4、11无论在哪种偏好分析中均居前三位,而采油厂2、3则处于第4、5位,而其他采油厂的大体排序趋势相同,仅部分单元变化较大。

4 结论

本文针对绩效评价中的评估偏好问题,结合企业绩效指标的设定,对原有DEA模型进行权重制定,使其能够实现多维偏好的绩效评估；同时,考虑现有DEA模型对有效评价单元不能全排序的现实,通过虚拟最优前沿面和最差前沿面的形式,借鉴TOPSIS的理念,综合考虑以DEA分析过程中评价单元与最优理想点和最差理想点的距离,建立相对贴近度排序指数公式,以此作为排序依据。通过12家采油厂的实际数据进行分析,以油气生产、安全生产和环保生产为优先条件对采油厂绩效进行了评估排序,验证了改进TOPSIS-DEA模型方法在采油厂绩效评估优选中的实用意义。

[1] Lozano S,Villa G.Centralized Resource Allocation Using Data Envelopment Analysis[J].Journal of Productivity Analysis,2004,12(22):143-161.

[2] Jahashahloo R,Hosseinzaden F,Shoja N,et al.A Method for Detecting Influential Observations in Radial DEA Models[J].Applied Mathematics and Computation,2004,2(147):415-421.

[3] Charnes A,Cooper W,Wei Q L,et al.Cone Ratio Data Envelopment Analysis and Multi-objective Programming[J].International Journal of Systems Science,1989,20(7):1099-1118.

[4] Wei Q L,Yu G.Analyzing the Properties of K-cone in Generalized Data Envelopment Analysis Model[J].Journal of Econometrics,1997:80(8),63-84.

[5] 杨 峰,梁 樑,查 勇，等.基于完全包络面的DEA Super效率评价方法[J].管理科学,2008,21(4):69-75. Yang Feng,Liang Liang,Zha Yong,et al.DEA Super Efficiency Evaluation Model Based on the Complete Envelopment Frontier[J].Journal of Management Sciences,2008,21(4):69-75.

[6] 卞亦文,许 皓.基于虚拟包络面和TOPSIS的DEA排序方法[J].系统工程理论与实践,2013,33(2):482-488. Bian Yiwen,Xu Hao.DEA Ranking Method Based upon Virtual Envelopment Frontier and TOPSIS[J].Systems Engineering-Theory & Practice,2013,33(2):482-488.

[7] 魏新强,张宝生.反向思维的定权重DEA中国能源效率分析[J].技术经济与管理研究，2013,30(1):3-6. Wei Xinqiang,Zhang Baosheng.China’s Energy Efficiency Analysis Based on Fixed Weight DEA Model Using Reverse Engineering Theory[J].Technoeconomics & Management Research,2013,30(1):3-6.

[8] Wei Xinqiang,Zhang Baosheng,Wang Qing.Improved TOPSIS Model Based on Interval Numbers[J].WIT Transactions on Information and Communication Technologies,2013,(48):55-61.

[9] 赵 东,王 震,赵 林,等.国际油气勘探开发项目风险分级与排序模型的构建及应用[J].中国石油大学学报(自然科学版),2010,34(1):164-169. Zhao Dong,Wang Zhen,Zhao Lin,et al.Construction and Application of Risk Rating and Ranking Model for International Oil and Gas Exploration & Production Projects[J].Journal of China University of Petroleum(Edition of Natural Science),2010,34(1):164-169.

[10] 马占新,任慧龙,戴仰山.DEA方法在多风险事件综合评价中的应用研究[J].系统工程与电子技术,2001,23(8):7-11. Ma Zhanxin,Ren Huilong,Dai Yangshan.Study of Applying DEA Method to Evaluate Events Under Multiple Risks[J].Systems Engineering and Electronics,2001,23(8):7-11.

2014-12-24

国家社会科学基金重大项目(13&ZD 159)；国家科技重大专项“煤层气开发经济评价技术研究”(2011 ZX 05038-004-01)

刘 岩(1986-),男,吉林松原人,博士研究生,主要从事项目管理、石油投资经济评价等工作。

10.3969/j.issn.1006-5539.2015.04.022