直流偏磁下的变压器振动仿真与试验

汪金刚，毛凯，段旭，杨永明，李珂

（1.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044; 2.国网山东省电力公司济南供电公司，山东济南 250012）

直流偏磁下的变压器振动仿真与试验

汪金刚1，毛凯1，段旭2，杨永明1，李珂1

（1.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044; 2.国网山东省电力公司济南供电公司，山东济南 250012）

针对变压器实际运行中经常会出现振动异常现象的问题，结合变压器铁心和绕组的振动机理，给出了变压器铁心和绕组所受电磁力方程和位移方程。利用COMSOL电磁场模块中的瞬态电流源建立电场模型，然后选择感应电流单元以电场模型计算结果作为激励源建立磁场模型，实现第一次电磁场的耦合建模。利用结构力学模块中实体应力应变部分建立结构力场模型，将电磁场耦合计算出的电磁力结果作为载荷加到力场模型中，实现第二次耦合，并最终得到发生直流偏磁时变压器内部磁通密度、机械应力分布、张力分布以及位移场分布的变化规律。通过搭建变压器振动试验平台，验证了铁心振动仿真模型、绕组振动仿真模型的正确性。

电磁场—结构力场耦合;直流偏磁;变压器振动;铁心;绕组

0 引言

电力变压器作为电力主干网络的一部分，其运行的可靠性对整个电力系统意义重大。然而在实际运行过程中，变压器经常会出现振动异常的问题［1］，究其原因，直流偏磁是导致变压器发生振动异常现象的重要原因之一［2－5］。直流偏磁下变压器铁心和绕组的形变会直接或间接导致变压器出现振动异常故障甚至损害变压器，但这种故障隐患难以通过常规电气试验来诊断。目前，国内外在变压器振动异常研究方面取得了一些成就，文献［6］通过对采集到的变压器瞬态振动信号进行时频分析，考察了变压器的机械故障（例如绕组螺丝松动等），提出了一种基于声振法的判断变压器铁心和绕组工况条件的方法;文献［7］利用磁致伸缩的磁特性分析了变压器结构形变以及铁心的振动，通过该方法可以计算得到变压器振动的特征频率;文献［8］就直流偏磁状态下电力变压器励磁电流进行了试验与分析;文献［9］对直流偏磁下变压器三维非线性涡流和损耗分布进行了计算;文献［10－11］对单相和三相变压器直流偏磁励磁电流进行了计算，对谐波分布以及磁滞回线测量进行了研究;文献［12－13］针对直流偏磁条件下励磁电流的实验和变压器直流偏磁的电路－磁路模型展开了研究。

现有的对变压器振动的研究还处于起步阶段，特别是对直流偏磁导致变压器振动异常的变化规律的研究还有很多不足之处。为此本文对直流偏磁量与变压器振动特性之间的关系开展了仿真与试验研究，探索了直流偏磁下变压器铁心和绕组受直流偏磁影响的变化规律，通过仿真考察直流偏磁对变压器内部磁通密度分布的影响，进而与机械结构力场耦合，结合经典牛顿力学分析直流偏磁引起的变压器铁心和绕组机械应力、张力以及位移场分布的变化规律，并搭建了变压器振动试验平台来验证仿真模型的正确性。

1 变压器振动机理

1.1 铁心振动机理

变压器铁心的硅钢片在交变磁场的作用下，会发生磁致伸缩效应，使得铁心对励磁频率的变化做周期性振动。磁致伸缩变化周期是电源频率的半个周期，故磁致伸缩引起的铁心振动是以两倍电源频率（即100 Hz）为基频［14］。随着变压器制造工艺的发展，铁心叠压方式的改进和铁心柱、铁轭采用无纬环氧玻璃粘带绑扎，使得硅钢片接缝处、叠片间电磁力引起的铁心振动很小［15］。因此，在铁心预应力足够大、硅钢片结合足够紧密时可认为，铁心的振动主要取决于硅钢片的磁致伸缩。由于铁心磁致伸缩的非线性及沿铁心内、外框的磁通路径长短不同，铁心振动频谱中除基频外，还包含高次谐波。当铁心压紧不够，发生松动或硅钢片的自重使铁心弯曲变形时，磁致伸缩增大，铁心振动变大［16］。

1.2 绕组振动机理

变压器绕组作为载流导体处在漏磁场中，在这些导体上作用着交变磁场产生的电动力（与流过绕组的电流平方成正比，且几乎全部的频谱分量都集中在基频处［17］），这些周期性的电动力使得变压器绕组产生机械振动，并传递到变压器结构的其它部件上。高、低压绕组之一在变形、位移或崩塌后，绕组的压紧不够，使高、低压绕组间高度差逐渐扩大，加剧绕组安匝不平衡，漏磁造成的电场力增大，从而使绕组振动加剧。相对于正常状态下的振动信号，原频率处的幅值也会发生变化，且绕组位移、松动或变形越严重，原频率处幅值变化越大［18］。

1.3 直流偏磁状态下的变压器振动机理

变压器发生直流偏磁现象时，与直流偏磁一致的半个周波的铁心磁通密度大大增加，另外半个周波的铁心磁通密度反而减小，磁通密度呈现出明显的正负半波不对称。铁心磁致伸缩率随磁通密度的增大而增大，由于直流偏磁后，铁心磁通密度在直流偏磁方向一致的半个周波大大增加，导致了硅钢片磁致伸缩率也增大，从而导致了铁心振动幅值的增大。

直流偏磁时变压器会发生铁心半波饱和现象，导致铁心磁导率大幅减小，从而使得变压器漏磁通大量增加，同时由于铁心半波饱和还会导致变压器励磁电流的增大，变压器绕组电流也会相应增加，从而铁心接缝电磁吸引力和器身的磁致伸缩率会随之增大。绕组电流的增大还导致了绕组电磁力的增大，这都加剧了变压器的振动。

2 仿真模型建立

变压器直流偏磁下的振动问题分析实际上是一个多物理场耦合问题的研究过程。首先利用COMSOL电磁场模块中的瞬态电流源建立电场模型，然后选择感应电流单元以电场模型计算结果作为激励源建立磁场模型，实现第一次电磁场的耦合建模，考察直流偏磁下电磁场的分布。而后利用结构力学模块中实体应力应变部分建立结构力场模型，将电磁场耦合计算出的电磁力结果作为载荷加到力场模型中，实现第二次耦合，并最终得到变压器的应力、张力、位移场分布等结果。

2.1 铁心和绕组振动源的电磁力数学模型

考虑硅钢片磁致伸缩和磁化特性的各向异性，变压器铁心磁－机械强耦合数值模型为［19］:

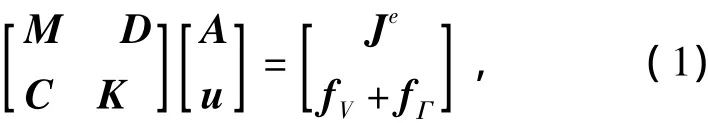
式中，M和K分别为磁弹性系数矩阵和机械弹性系数矩阵;C，D为磁－机械的耦合作用矩阵，满足C =DT，其中D表示机械振动对磁场分布的影响矩阵，C表示磁场对铁心振动的贡献矩阵;A为引入的矢量磁位;u为铁心的振动位移;Je表示外部电流密度;fV和fΓ分别为变压器铁心受外部体积力和铁心表面受到的边界面力。

式（1）矩阵各元素的分量都是沿x、y、z三个正交方向，采用牛顿－拉夫逊法（Newton-Raphson）求解，由于变压器铁心的硅钢片具有各向异性，在求解时要进行铁磁材料的牛顿－拉夫逊非线性处理。且磁通在铁心的分布虽然集中在xy平面内，但在铁心搭迭间隙（即铁心振动集中体现处）存在z方向的磁通。于是考虑按线性、各向同性来计算z方向的磁场力。基于简化的励磁模型，考虑铁心材料为线性、各向同性的铁磁材料，其所受的磁场力的体积力密度表达式为［20］:

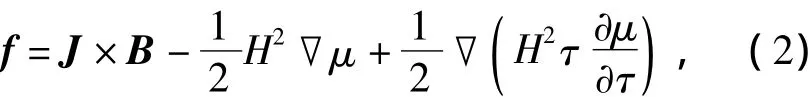
式中，f为体积力密度，J为电流密度，B为磁感应强度（磁通密度），H为磁场强度大小，μ为介质的磁导率，τ为介质的体积密度。公式（2）中第一项表示洛仑兹力，第二项表示材料体积力，第三项表征磁致伸缩现象。

当有直流偏磁时，变压器绕组的振动为受迫振动，考虑到作用在绕组上的电磁力与电流的平方成正比，以及变压器稳定运行时的电气量激励具有周期性特点，可以得出直流偏磁下变压器绕组所受的电磁力表达式和位移方程:

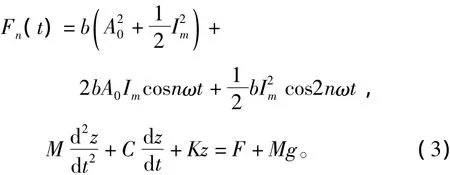
2.2 电磁场模型建立

本文选用一台5kVA高低压侧电压均为400 V的三相干式变压器作为建模对象，重点考察变压器铁心以及线圈振动与模拟直流偏磁之间的关系，对实际物理模型进行了合理简化，建立二分之一模型进行分析。在电场模块下建立电场方程:

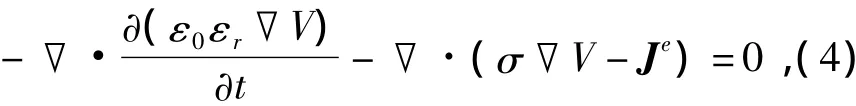
其中，ε0为自由空间的介电常数，其大小为8.85× 10－12F/M，εr为相对介电常数，σ为电导率，Je为外部电流密度，V为方程因变量，即电势。

在电磁场分析中，应用场路耦合法将变压器的物理模型和电路模型耦合到一起，其外电路电路图如图1所示。将计算得到的外部电流密度作为磁场中的激励加到磁场模块中，磁场的求解域方程为:

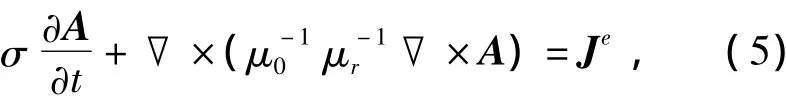
其中，μ0为自由空间的磁导率，其大小为4π×10－7H/m，μr为相对磁导率，A为方程因变量，即矢量磁位。

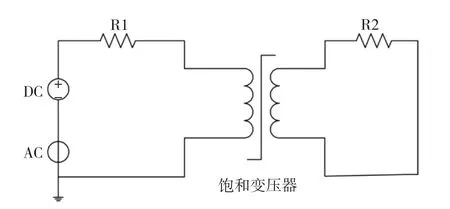
图1 系统仿真电路图Fig.1System simulation circuit diagram

采用场路耦合法建立模型使得造成直流偏磁的直流电压源加载更方便，另外，在电路模型中还可以考虑线圈电阻等条件，从而真实反应变压器的实际情况，提高仿真的准确性。通过计算可以得到变压器在各种直流偏置情况下的磁场分布情况，包括磁场强度H，磁通密度B等的分布。

在磁场分析过程中存在如下本构关系:

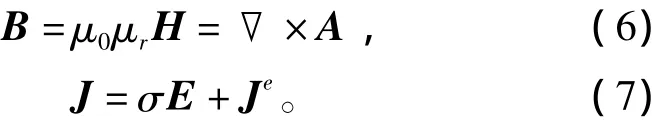
式中，Je为外部电流密度，E为电场强度。

2.3 结构力场模型建立

对实际的机械系统或结构系统的质量和弹性参数的精确求解十分困难，因而将其简化为离散系统，其中包括若干个集中质量的弹簧与阻尼器连接在一起。经离散化处理后，一个结构的动力学特性可以由N阶矩阵的微分方程来描述，在计算机中就可以通过仿真来实现。

在COMSOL结构力场分析过程中，选择实体应力模块，变量为（u，v，w），使用求解域方程为:

式中，m为质量矩阵，k为刚度矩阵，ξ为阻尼系数矩阵。

将计算得到的B、J带入结构力场求解域方程实现电磁场与结构力场的耦合，计算铁心以及绕组的受力情况和位移场分布。计算时，建模对象是干式变压器，因此将填充物设置为空气，并且在一个标准大气压下。绕组以及铁心选择COMSOL中材料库中的铜以及硅钢材料。

不同于以往仿真磁致材料伸缩特性时采用修改铁心弱解形式方法来实现，本文采用铁磁材料的非线性HB曲线来指定铁心硅钢片的本构关系，通过插值的方法来实现第一次耦合计算出来的磁密大小B与磁场大小H之间的对应关系。

3 仿真结果及分析

3.1 电磁场模型建立

首先得到变压器在无直流偏磁情况下的磁场分布，然后得到变压器在有直流偏磁情况下的分布情况，并将两部分做分析比较，考察不同直流偏磁情况下磁场的分布情况。

3.1.1 直流偏置电压UDC=0 V时磁场分布情况

图2为直流偏置电压为0 V时磁通密度B的分布情况，（a）、（b）分别是0.005 s以及0.015 s的计算结果，即励磁电流在一个周期正负半周极值是的计算结果。图2中的箭头大小比例反应了那一时刻磁通密度的分布情况，比较图2（a）、（b）我们可以发现励磁电流在正负半周期磁通密度极值以及磁场分布是相等的。

3.1.2 直流偏置电压UDC=1 0V时磁场分布情况

当直流偏置电压为10 V时，磁通密度B的正负半周期的分布不再平衡。仿真中，加入的偏置电压为正向偏置，因此，从图3中可以发现，在0.005 s时（即正半周期极值时刻）磁通密度要大于0.015 s时（即负半周期极值时刻）磁通密度的最大值，并且也大于无偏置电压时磁通密度的最大值。结合磁致伸缩系数相关理论就可以知道，这时，变压器铁心磁致伸缩将增大，也就导致了变压器振动的增强。

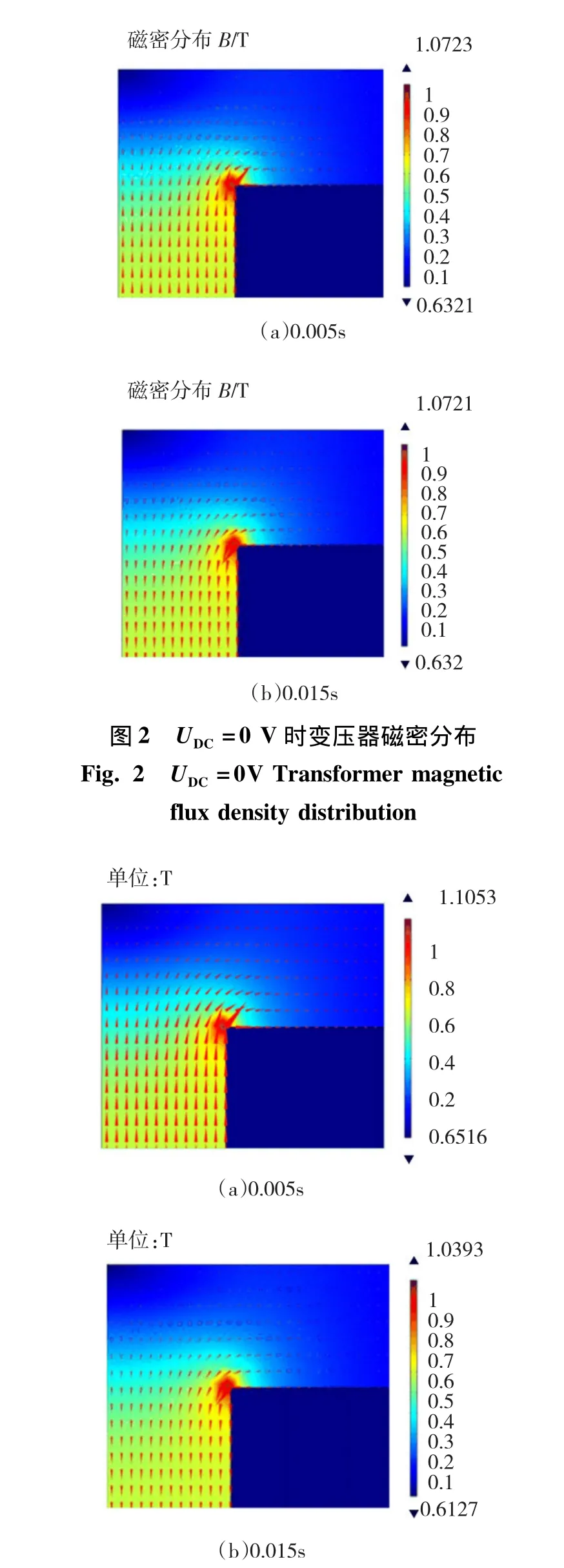
图3 UDC=10V时变压器磁密分布Fig.3UDC=10V Transformer magnetic flux density distribution

3.1.3 直流偏置电压UDC=20 V时磁场分布情况

从图4可知，当直流偏置电压增大时，正负半周期的磁通密度不平衡将更加明显，尤其是磁通密度极值的增大更加严重，也就致使铁心的磁致伸缩系数变的更大，变压器振动也更明显。

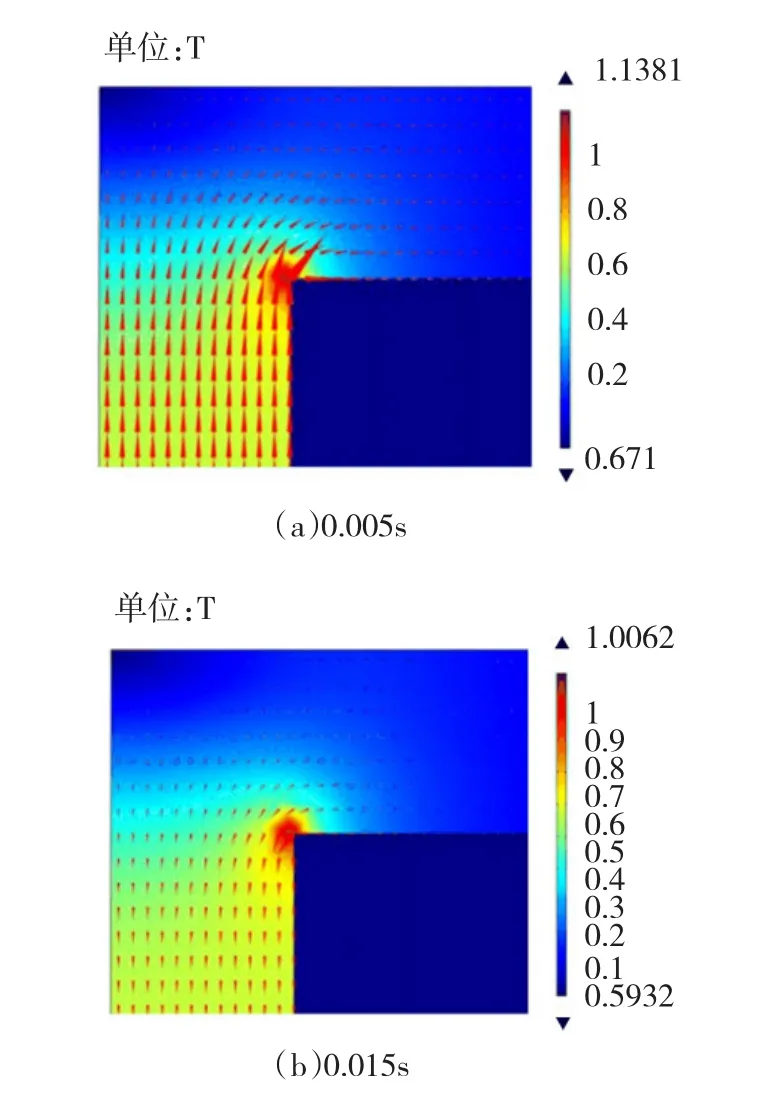
图4 UDC=20V时变压器磁密分布Fig.4UDC=20V Transformer magnetic flux density distribution

3.2 结构力场仿真结果分析

3.2.1 铁心应力、张力和位移场仿真计算

考虑到空载时变压器的振动主要来自于铁心振动这一特殊情况，所以，在建立铁心模型时本文是在变压器二次侧开路的情况下建立的，即模拟变压器空载时的情况。由于真实变压器铁心的上下铁轭都是通过加紧件固定住的，因此在建立模型时，我们也将该模型中铁心的上下边界固定。

图5～图7是直流偏置电压UDC=0 V时铁心应力、张力以及位移场的分布，都取0.002 5 s和0.007 5 s两个时刻的解，也就是正负半周最大值的情况。

图8～图10为直流偏置电压UDC=10 V时铁心应力、张力以及位移场的分布，同样也都取0.002 5 s和0.007 5 s两个时刻的解。

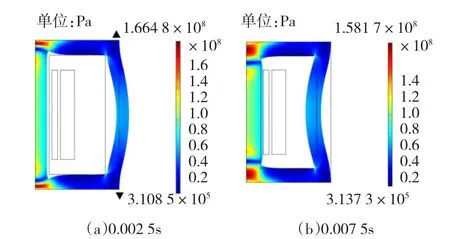
图5 UDC=0 V时铁心应力以及形变Fig.5UDC=0V The core stress and deformation

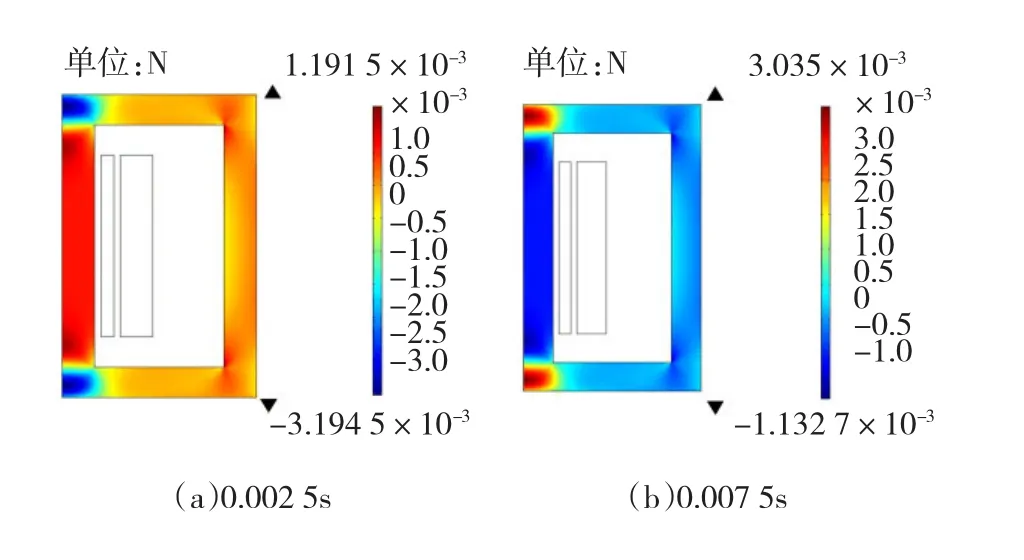
图6 UDC=0 V时铁心张力分布Fig.6UDC=0 V The core tension distribution

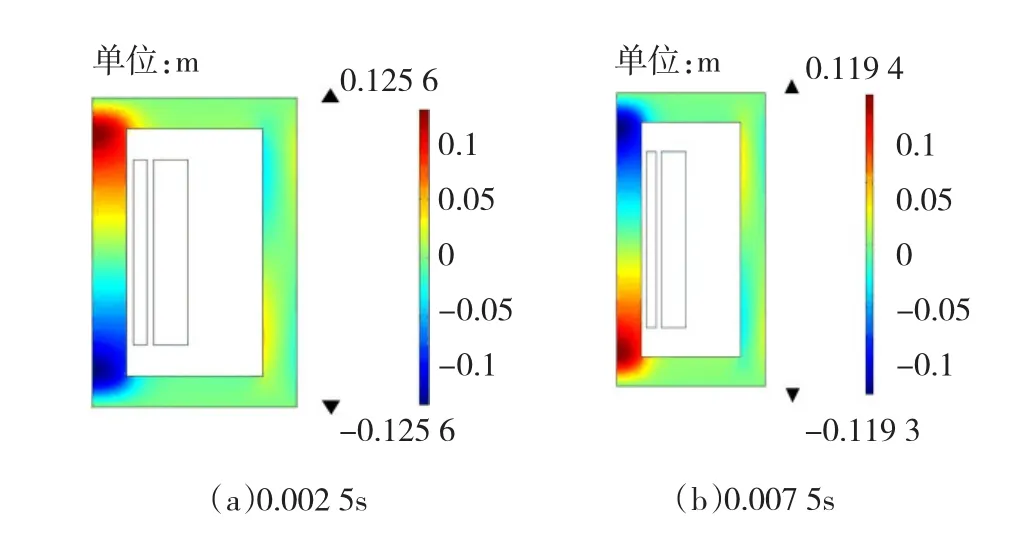
图7 UDC=0 V时铁心位移场分布Fig.7UDC=0 V The core displacement field distribution

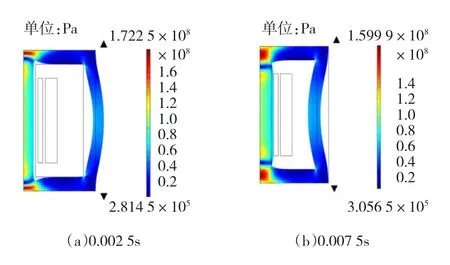
图8 UDC=10 V时铁心应力分布及形变Fig.8UDC=1 0V The core stress and deformation

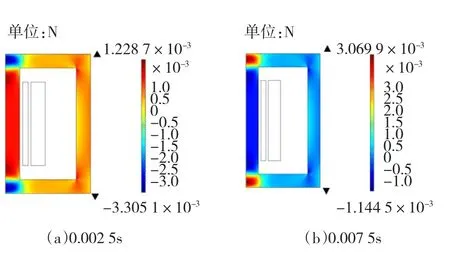
图9 UDC=10 V时铁心张力分布Fig.9UDC=10 V The core tension distribution

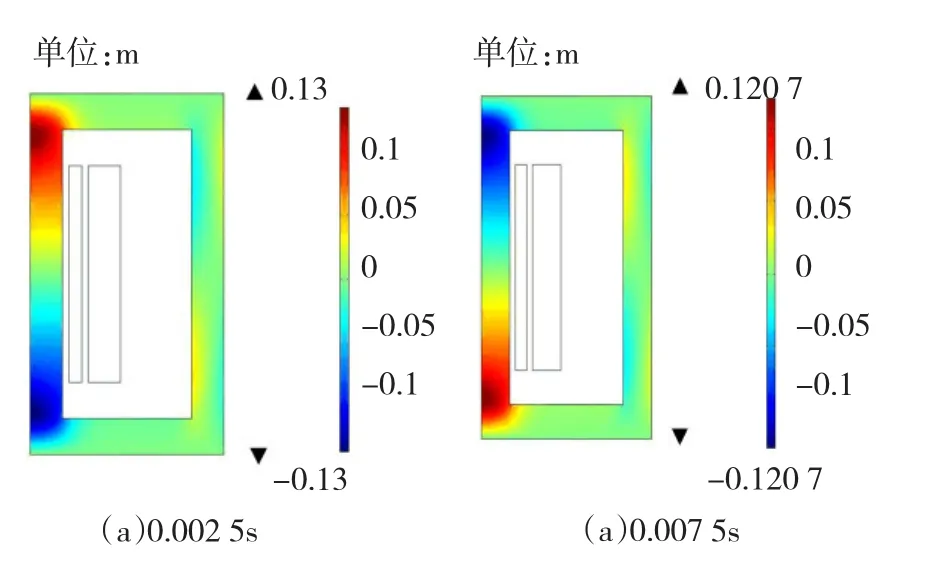
图10 UDC=10 V时铁心位移场分布Fig.10UDC=10 V The core displacement field distribution

UDC=20 V时铁心的应力、张力以及位移场的分布，限于篇幅不一一贴上仿真结果。日本M.Mizokami等学者对三相三柱式变压器铁心模型在1.3 T和1.7 T的磁通密度情况下各个面均匀分布多点振动做了测试，给出了铁心表面各位置在两个不同磁通密度情况下的一些振动特性比较，得出结论［21］:振动主要出现在铁心的三个旁轭上，并且振动方向垂直于变压器铁心前表面;铁心前后两个面上的振动大于其他面上的振动。由图5和图8可以看出，整个铁心应力分布的最大值的位置是在旁轭上，也是振动最明显的地方，这与日本M.Mizokami等学者对三相三柱式变压器铁心模型所做的振动测试研究所得的结论一致，表明该分析方法的正确性。

3.2.2 绕组应力、张力和位移场仿真计算

变压器的绕组在安装时通常在绕组的顶端和低端会施加充足的预应力来保证绕组线圈的稳定性，所以在仿真计算时，将绕组线圈的上下边界进行了限制。由于计算的是时变解，这里统一都取0.01 s这一时刻的数值解。当变压器处于短路情况时，其绕组的振动最大，因此在求解结果时，将变压器的二次侧短路进行求解。

图11和图12分别为直流偏置电压UDC=0 V时变压器一次绕组和二次绕组的应力、张力以及位移场的分布。

图13和图14分别为直流偏置电压UDC=10 V时变压器一次绕组和二次绕组的应力、张力以及位移场的分布。

UDC=20 V时一次绕组和二次绕组的应力、张力以及位移场的分布，在此亦限于篇幅不一一贴上仿真结果。比较不同直流偏置电压下一次绕组线圈与二次绕组线圈的位移场能够发现，随着偏置量的增大，位移场的峰值显著增加，当偏置量增加了20 V时，在0.01 s这一时刻一次绕组线圈的位移幅值增加了17%，二次绕组线圈由于所处漏磁场磁密较小，因此变化不太明显。

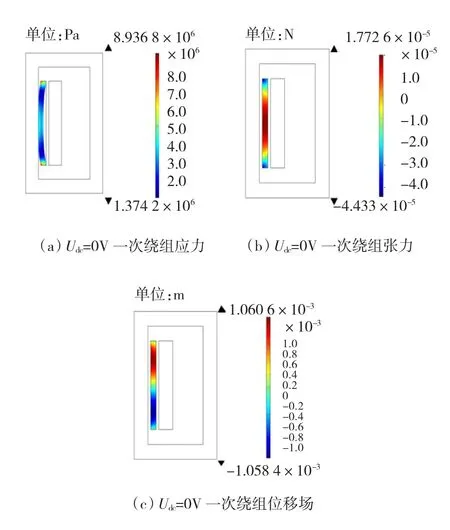
图11 UDC=0V时一次绕组应力、张力、位移场分布Fig.11UDC=0V Primary winding stress，strain，displacement field distribution

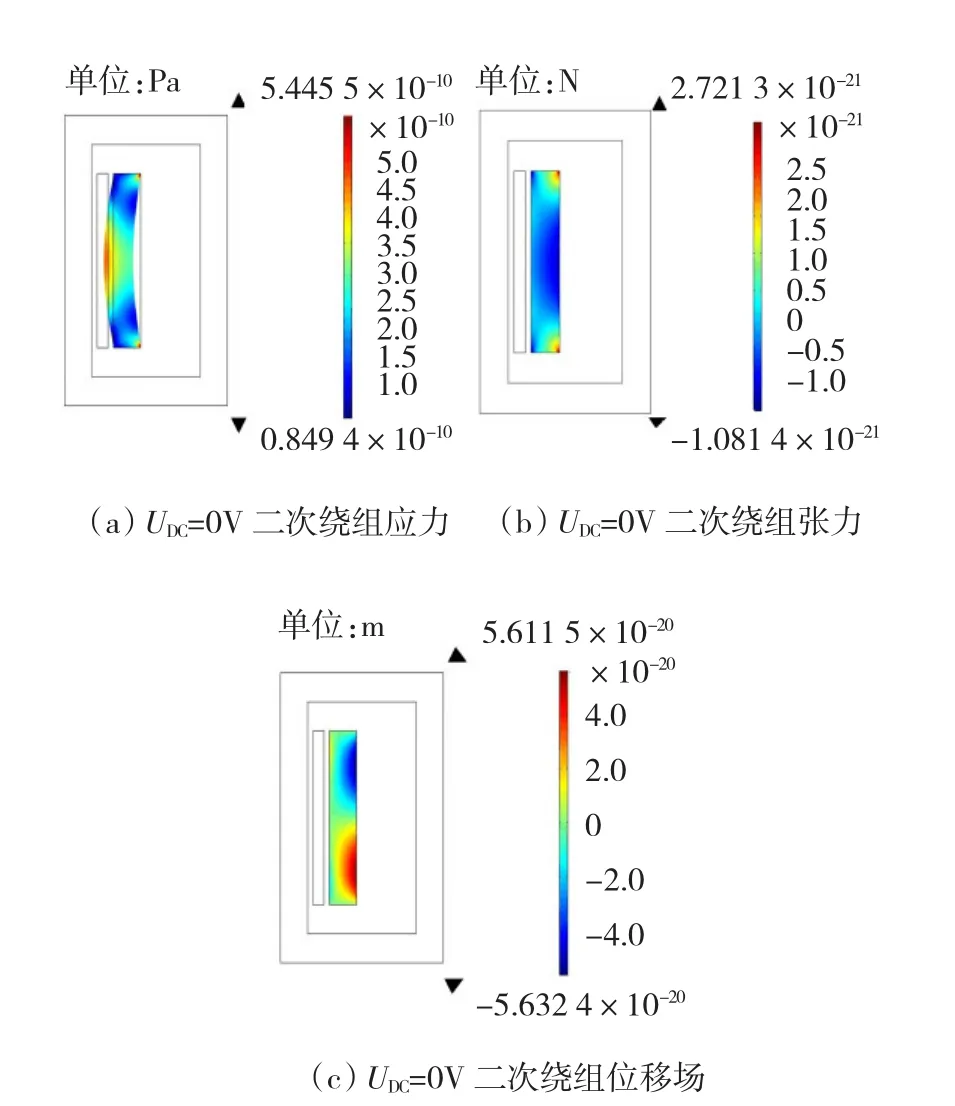
图12 UDC=0V时二次绕组应力、张力、位移场分布Fig.12UDC=0V Secondary winding stress，strain，displacement field distribution

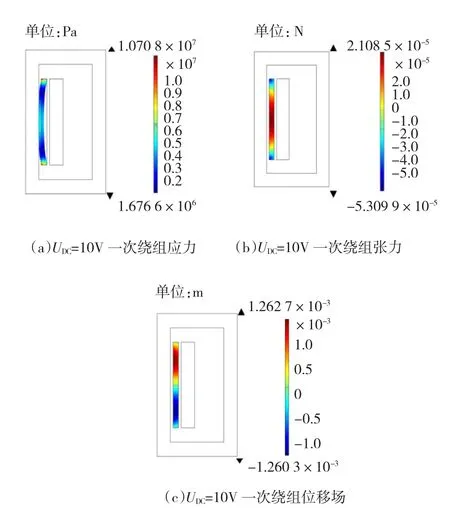
图13 UDC=10V时一次绕组应力、张力、位移场分布Fig.13UDC=10V Primary winding stress，strain，displacement field distribution

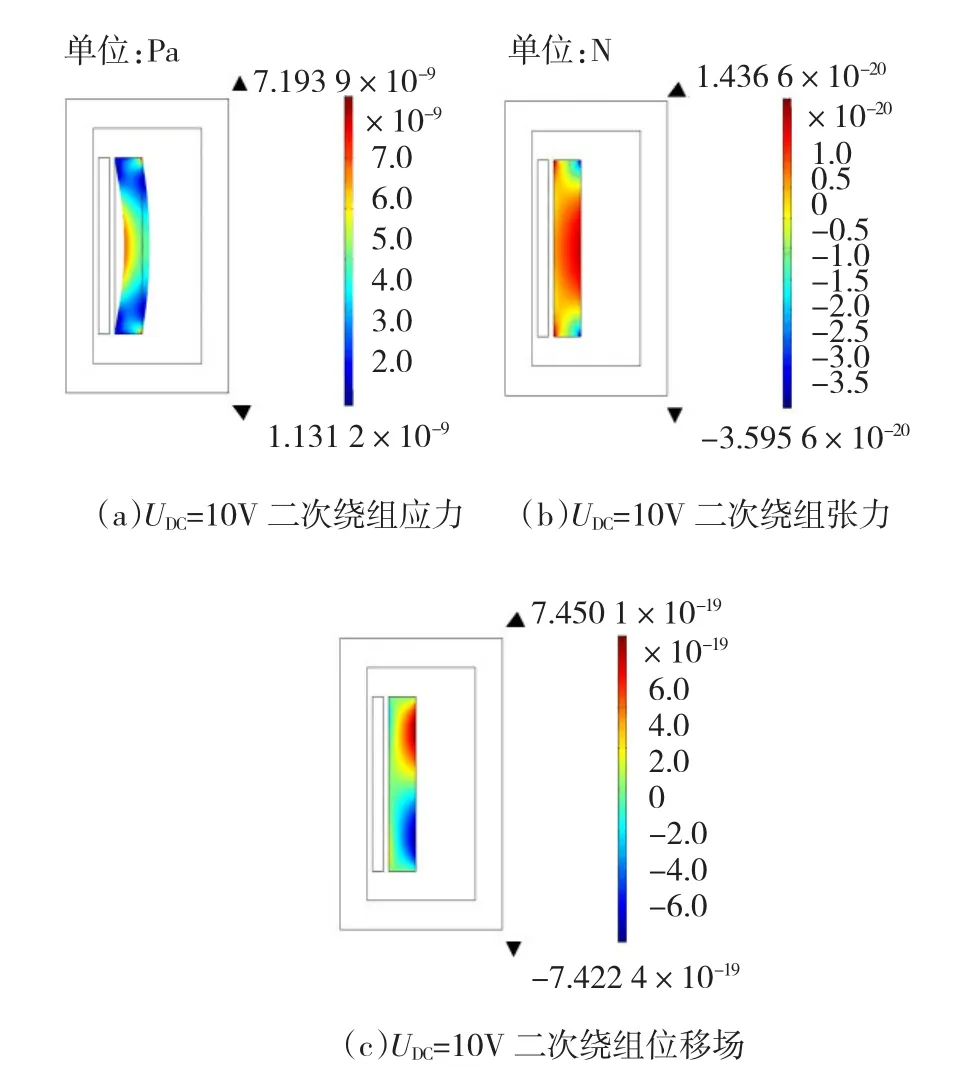
图14 UDC=10V时二次绕组应力、张力、位移场分布Fig.14UDC=10V Secondary winding stress，strain，displacement field distribution

4 试验研究

为了验证模型的正确性，本文搭建了变压器振动试验平台。试验平台主要由前端LC0166T型加速度传感器、LC0201－3信号调理器、研华PCI－1714UL数据采集卡和基于虚拟仪器技术的人机界面及后台数据库监测系统平台组成。

试验变压器为三相干式变压器，主要参数为:额定容量5 kVA，电压等级为400/400 V，空载电流I0为12%，空载损耗75 W，短路损耗160 W，短路电压3.5%。作为主磁通通路的硅钢片附近是变压器振动较为明显的地方，同时可以直接准确的测得绕在铁心柱上的绕组线圈的振动情况，因此，采用三个加速度传感器置于试验变压器A、B、C三相铁心较小，因此变化不太明显。

柱对应的器身外面，如图15所示。为了验证方便，本文对仿真模型和实测试验都取直流偏置电压UDC=0V时的情况来做对比。

图15 加速度传感器分布Fig.15Distribution of acceleration sensor

4.1 铁心振动仿真模型验证

变压器在空载运行时，其器身的振动主要是铁心的振动，所以在铁心的结构力场仿真中取变压器空载运行时旁轭上所受应力最大的点计算其振动加速度曲线，并绘制相应的频谱图，结果如图16所示。

让试验变压器空载运行，通过试验由加速度传感器测得变压器振动的波形和频谱。试验时，B相的波形和频谱最为明显，如图17所示。

比较图16和图17可以发现，仿真模型与实测的数据都含有200 Hz、300 Hz、400 Hz、500 Hz的波峰，但仿真产生的加速度曲线中含有大量的毛刺，所以在仿真模型中含有大量的高次谐波。在仿真模型中100 Hz这一频带较宽，而在实测的数据中却并不明显，这是因为变压器铁心振动的频率分布大部分都集中在100 Hz这一频带上，相反实测的变压器振动数据是铁心在各种机械约束和与其他机械部件共振的情况下测得的，其100 Hz的频带并不明显。因此，本文所建立的仿真模型还是能够比较好的模拟实际变压器铁心振动的情况。在仿真中出现的毛刺，主要是由仿真出的振动加速度信号中存在高频引起的，而这些高频信号是在电磁场和机械力场之间耦合的过程中产生的，造成这一现象的主要原因是:

1）铁心的磁致伸缩非线性特性。

2）绕组建模时设定为线圈，从而导致的各个线饼之间以及线饼两端约束振动的刚度系数的不同造成的非线性。

3）仿真步长的设定造成仿真结果中出现毛刺，也就是数据的突变。当仿真的步长变短时，仿真出的曲线毛刺会减少并且平滑，但是当仿真步长取的过短，会占用大量的计算机内存，由于计算条件有限，不可能将仿真步长设定的足够短。

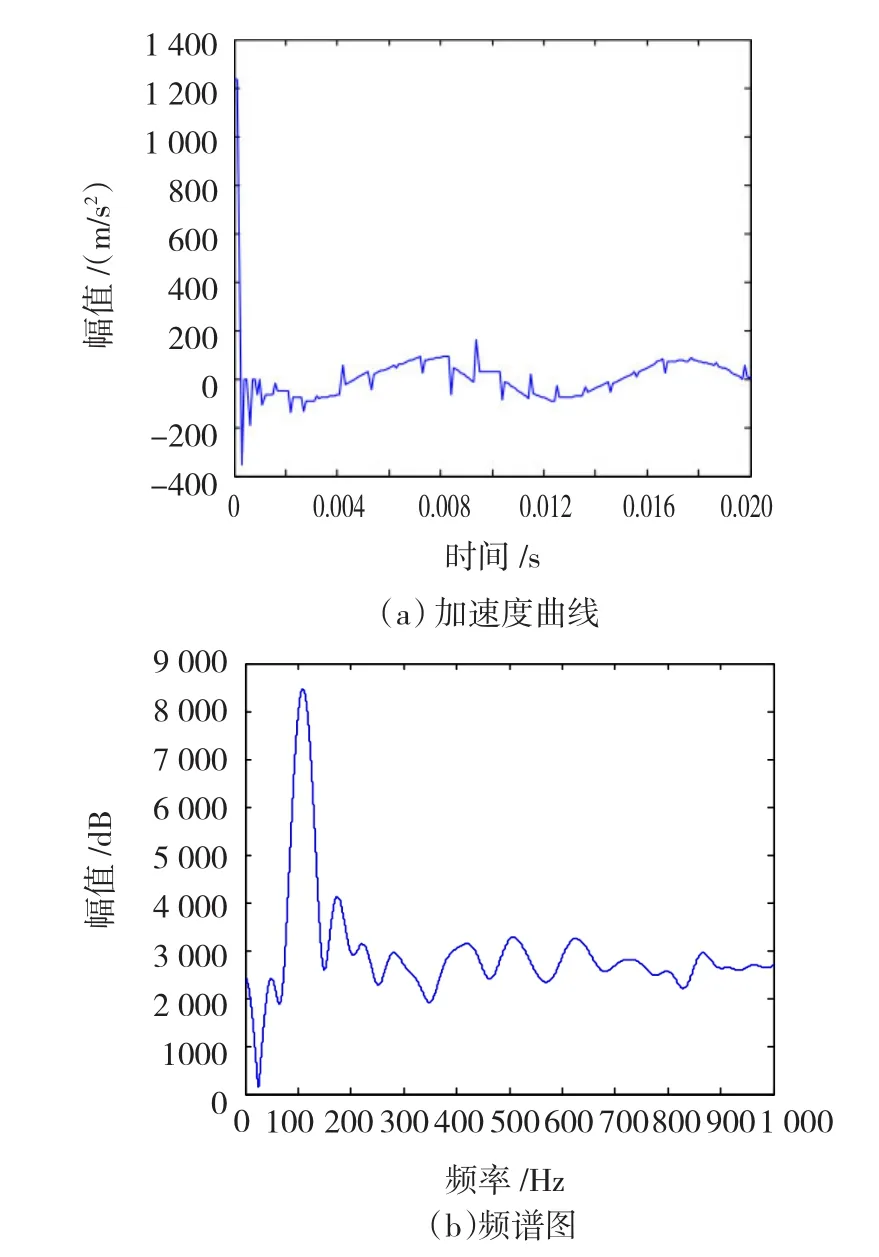
图16 铁心仿真模型振动加速度曲线及频谱Fig.16Simulation model vibration acceleration waveform and spectrum for the core

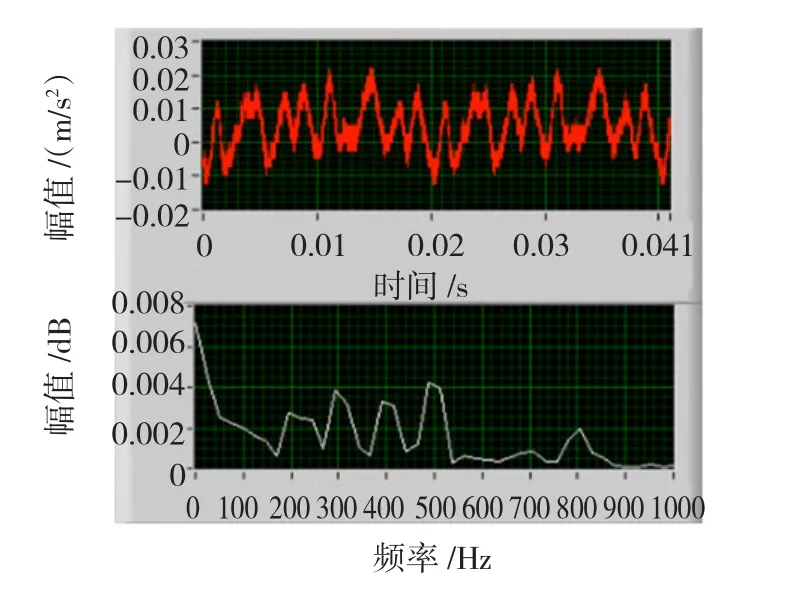
图17 空载时变压器B相振动波形及频谱Fig.17Transformer B－phase vibration waveform and spectrum on no-load

4.2 绕组振动仿真模型验证

由于短路情况下变压器器身的振动主要来自于绕组，所以在绕组的结构力场仿真中求解这一情况下绕组的振动加速度数据与实测的数据比较即可验证模型。绕组的振动加速度曲线及频谱图如图18所示。

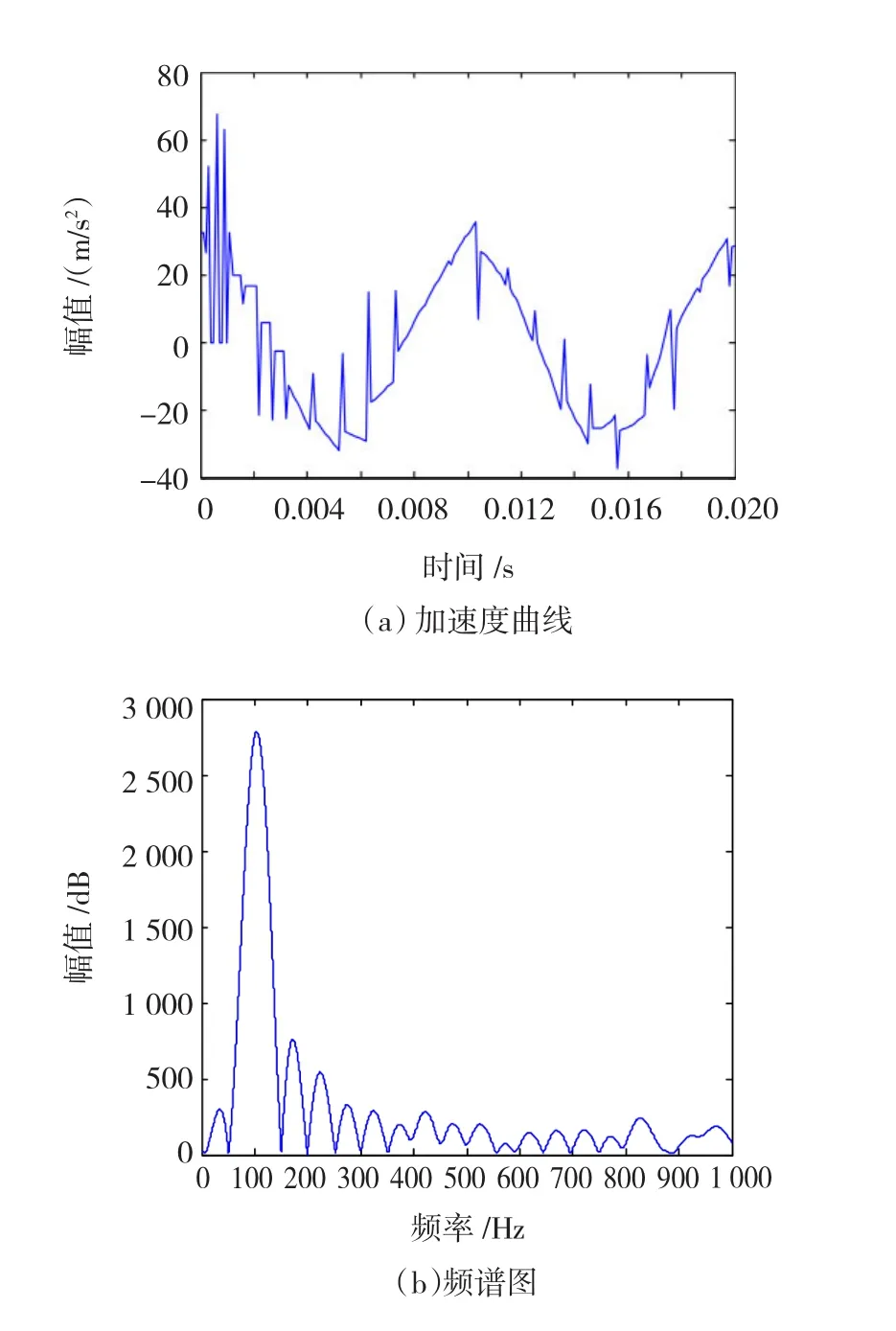
图18 绕组仿真模型振动加速度曲线及频谱Fig.18Simulation model vibration acceleration curve and spectrum for the winding

让试验变压器二次侧短路运行，加速度传感器测得的B相的数据也较A、C相最为明显，如图19所示。

比较图18和图19可以看出，仿真出的波形含有较多的毛刺，但整体波形与实测的变压器振动波形仍然非常相似，实测波形中的凸起部分在仿真波形中的对应位置有比较高的毛刺。从各自的频谱图来看，其振动加速度的主要频带都集中于100～500 Hz之间，并且主要的就是100 Hz、200 Hz和300 Hz三个频带，其他高频部分含量较少，仿真波形中的高频含量同铁心的仿真讨论过一样，都是由于波形的毛刺所导致的。因此，总的来说，仿真模型能够与实测的数据较好的吻合，说明了仿真模型的正确。

5 结论

本文结合变压器铁心和绕组的振动机理，给出了直流偏磁下变压器铁心和绕组受电磁力激励振动的数学模型，并将得出的数学模型应用到变压器的耦合场建模分析中。建立了直流偏磁影响下的变压器内部磁通密度分布的数值模型，考察了当直流偏磁发生时激励的正负半周期变压器内部磁通密度的变化规律，明显的观察到在正负半周期内磁通密度的分布是不相同的。在建立了变压器铁心和绕组电磁场模型的基础上，耦合了考虑铁磁材料磁致伸缩的结构力场，用于研究直流偏磁对变压器内部应力、张力以及位移场分布的影响规律，绘制了铁心和绕组的振动加速度曲线，经与试验平台实测数据结果对比，验证了模型的正确性。

［1］PRICE P R.Geomagnetically induced current effects on transformer＇s［J］.IEEE Transactions on Power Delivery，2002，17（4）:1002－1008.

［2］刘连光，刘春明，张冰，等.中国广东电网的几次强磁暴影响事件［J］.地球物理学报，2008，51（4）:976－981.

LIU Lianguang，LIU Chunming，ZHANG Bing，et al.Strong magnetic storm＇s influence on China＇s Guangdong power grid［J］.Chinese Journal of Geophysics，2008，51（4）:976－981.

［3］张建平，潘星.500kV变压器异常噪声与振动的原因分析［J］.浙江电力，2006，3（6）:6－10.

ZHANG Jianping，PAN Xing.Analysis for abnormal noise and mechanical vibration of 500kV transformer［J］.Zhejiang Electric Power，2006，3（6）:6－10.

［4］蒯狄正，刘成民，万达.直流偏磁对变压器影响的研究［J］.江苏电机工程，2004，23（3）:1－5.

KUAI Dizheng，LIU Chengmin，WAN Da.Experiment and research of the influence of direct－current magnetic bias on transformer［J］.Jiangsu Electrical Engineering，2004，23（3）:1－5.

［5］刘林玉，谢学武.500kV主变压器异常声音分析［J］.高电压技术，2005，31（4）:85－87.

LIU Linyu，XIE Xuewu.Analysis of increase of noise of 500kV transformer［J］.High Voltage Engineering，2005，31（4）:85－87.

［6］BORUCKI S.Diagnosis of technical condition of power transformers based on the analysis of vibroacoustic signals measured in transient operating conditions［J］.IEEE Transactions on Power Delivery，2012，27（2）:670－676.

［7］KITAGAWA W，ISHIHARA Y，TODAKA T，et al.Analysis of structural deformation and vibration of a transformer core by using magnetic property of magnetostriction［J］.Electrical Engineering in Japan，2010，172（1）:19－26.

［8］赵志刚，刘福贵，张俊杰，等.直流偏磁条件下变压器励磁电流的实验与分析［J］.电工技术学报，2010，25（4）:71－76.

ZHAO Zhigang，LIU Fugui，ZHANG Junjie，et al.Measurement and analysis of magnetizing current in DC－biased transformers［J］.Transactions of China Electrotechnical Society，2010，25（4）: 71－76.

［9］YAO Y Y，KOH C S，NI G Z，et al.3－D nonlinear transient eddy current calculation of online power transformer under DC bias［J］.IEEE Transactions on Magnetics，2005，41（5）:1840－1843.

［10］李晓萍，文习山，樊亚东，等.直流入侵三相三柱变压器励磁电流及谐波计算［J］.高电压技术，2006，32（5）:69－72.

LI Xiaoping，WEN Xishan，FAN Yadong，et al.Computation of exciting current and harmonic for three－phase and three limbs transformer under DC inrushing［J］.High Voltage Engineering，2006，32（5）:69－72.

［11］李晓萍，文习山，蓝磊，等.单相变压器直流偏磁试验与仿真［J］.中国电机工程学报，2007，27（9）:33－40.

LI Xiaoping，WEN Xishan，LAN Lei，et al.Test and simulation for single－phase transformer under DC bias［J］.Proceedings of the CSEE，2007，27（9）:33－40.

［12］李泓志，崔翔，卢铁兵，等.变压器直流偏磁的电路－磁路模型［J］.中国电机工程学报，2009，29（27）:119－125.

LI Hongzhi，CUI Xiang，LU Tiebing，et al.Electric circuit and magnetic circuit combined model of DC biased power transformer［J］.Proceedings of the CSEE，2009，29（27）:119－125.

［13］李慧奇，崔翔，候永亮，等.直流偏磁下变压器励磁电流的实验研究及计算［J］.华北电力大学学报，2007，34（4）:1－6.

LI Huiqi，CUI Xiang，HOU Yongliang，et al.Experimental studies and calculations of the exciting current in the transformer under DC bias magnetization［J］.Journal of North China Electric Power University，2007，34（4）:1－6.

［14］万庆涛.基于LabVIEW的电力变压器在线状态监测系统的研究［D］:兰州大学通信工程专业;2008:15－28.

［15］顾晓安，沈荣瀛，徐基泰.大型电力变压器振动和噪声控制方法研究［J］.噪声与振动控制，2001（5）:7－11.

GU Xiaoan，SHEN Rongying，XU Jitai.Study on the vibration and noise control techniquesin large power transformers［J］.Noise and Vibration Control，2001（5）:7－11.

［16］程锦，李延沐，汲胜昌，等.振动法在线监测变压器绕组及铁心状况［J］.高电压技术，2005，31（4）:43－45，48.

CHENG Jin，Li Yanmu，Ji Shengchang，et al.Application of vibration method on monitoring the winding and core condition of transformer［J］.High Voltage Engineering，2005，31（4）:43－45.

［17］郭俊，汲胜昌，沈琪，等.盲源分离技术在振动法检测变压器故障中的应用［J］.电工技术学报，2012，10（27）:68－78.

GUO Jun，JI Shengchang，SHEN Qi，et al.Blind source separation technology for the detection of transformer fault based on vibration method［J］.Transactions of China Electrotechnical Society，2012，10（27）:68－78.

［18］汲胜昌，王世山，李清泉，等.用振动信号分析法监测变压器绕组状况［J］.高电压技术，2002，28（4）:12－13+15.

JI Shengchang，WANG Shishan，LI Qingquan，et al.The application of vibration method in monitoring the condition of transformer winding［J］.High Voltage Engineering，2002，28（4）:12－13 +15.

［19］祝丽花，杨庆新，闫荣格，等.考虑磁致伸缩效应电力变压器振动噪声的研究［J］.电工技术学报，2013，28（4）:1－6+19.

ZHU Lihua，YANG Qingxin，YAN Rongge，et al.Research on vibration and noise of power transformer cores including magnetostriction effects［J］.Transactions of China Electrotechnical Society，2013，28（4）:1－6+19.

［20］冯慈璋.静态电磁场［M］.2版.西安:西安交通大学出版社，1998:222－226.

［21］MIZOKAMI M，YABUMOTO M，OKAZAKI Y.Vibration analysis of a 3－phase model transformer core［J］.Electrical Engineering in Japan，1997，119（1）:1－8.

（编辑:张诗阁）

Simulation and test of transformer vibration under DC bias

WANG Jin-gang1，MAO Kai1，DUAN Xu2，YANG Yong-ming1，LI Ke1
（1.State Key Laboratory of Power Transmission Equipment＆System Security and New Technology，Chongqing University，Chongqing 400044，China;2.State Grid Shandong Electric Power Co.Jinan Power Supply Company，Jinan 250012，China）

Aiming at the abnormal vibration problem when a transformer actually operates and combining the transformer core with winding vibration mechanism，the electromagnetic force equations and displacement equations of transformer core and winding were provided.An electric field model was established by transient current source in COMSOL electromagnetic modules.A magnetic field model was established by the induced current unit where computation of field module was excitation source.Based on this，first coupled modeling of electromagnetic fields was established.The second coupled modeling of electromagnetic fields was set up when structure field module was established through the physical stress and strain section of structural mechanics module and the electromagnetic coupling electromagnetic force calculated as a result of the load applied to the force field model.At last，inside magnetic flux density of transformer，mechanical stress distribution，tension distribution and displacement distribution change rule under the DC bias influence were investigated.The vibration simulation models of core and winding are verified by building test platform.

electromagnetic-structure coupling field;DC bias;transformer vibration;core;the winding

10.15938/j.emc.2015.01.009

TM 743

A

1007－449X（2015）01－0058－10

2014－02－17

国家自然科学基金（51207175，51247008）

汪金刚（1979—），男，博士，副研究员，研究方向为电力设备故障检测与诊断、电磁测量技术等;

毛凯（1983—），男，硕士，研究方向为电工理论与新技术、电磁测量与传感;

段旭（1985—），男，博士，研究方向为电工理论与新技术、电磁测量与传感;

杨永明（1958—），女，博士，教授，博士生导师，研究方向为电力系统在线监测;

李珂（1987—），男，博士研究生，研究方向为电工理论与新技术、电磁测量与传感。

汪金刚