基于双目立体视觉的果蔬深度信息获取

乔方博， 曾松伟， 宋洪军,郜园园*

(1.浙江农林大学信息工程学院智慧农林业研究中心,浙江杭州 311300；2.北京交通大学电子信息工程学院，北京 100044；3.浙江省林业智能监测与信息技术研究重点实验室，浙江杭州 311300)



基于双目立体视觉的果蔬深度信息获取

乔方博1，2， 曾松伟1，3， 宋洪军1,3,郜园园1，3*

(1.浙江农林大学信息工程学院智慧农林业研究中心,浙江杭州 311300；2.北京交通大学电子信息工程学院，北京 100044；3.浙江省林业智能监测与信息技术研究重点实验室，浙江杭州 311300)

摘要针对果蔬采摘机械采摘过程中深度信息不易获的缺陷，该研究运用双目立体视觉技术通过摄像机标定对豆角的位姿信息进行获取。首先根据相机成像原理阐述图像坐标系、相机坐标系、世界坐标系三者之间的转换；其次通过对单目摄像机模型与平行相机模型之间的比较，推导双目相机定位算法；最后通过对试验结果的研究，分析该技术在不同场景应用过程中的注意事项，并对未来改进方向进行展望。

关键词深度信息；双目；立体视觉；摄像机标定

视觉是人类观察世界、认知世界的重要功能手段，人类感知外部世界主要通过视觉、触觉、听觉和嗅觉等感觉器官，其中80%的信息是由视觉获取的，机器视觉是人类利用计算机实现人的视觉功能一对客观世界三维场景的感知、识别和理解，机器视觉是一个相当新而且发展迅速的研究领域，机器视觉技术正广泛地应用于各个方面，许多人类无法感知的场合，如危险场景感知等，机器视觉更突显其优越性[1-3]。机器视觉属于影像的重构技术，具有非接触性测量、实施简易的特点，具有广阔的应用前景，是有待于进一步开发的领域。计算机视觉被认为是计算机科学和人工智能的一个分支，计算机视觉就是用机器代替人的眼睛和大脑，对客观世界进行感知和解释的技术。该系统的首要目标是使计算机具有通过一幅或者多幅二维图像认知周围的三维环境信息的能力。这种能力不仅可以使计算机能够感知三维环境中物体的几何信息，并且能够对它们进行描述、存储并使用图像来创建和恢复现实世界模型，从而达到认知现实世界的目的。因此，自从计算机视觉这门科学出现以来就成为计算机科学的重要研究领域之一并且发展十分迅速。笔者在对摄像机成像模型进行分析的基础上，以豆角为例，进行了果蔬位姿深度信息恢复试验，对未来基于双目立体视觉的果蔬深度信息获取的改进方向提出展望。

1摄像机成像模型

1.1图像坐标系、摄像机坐标系、世界坐标系摄像机主要的功能是把三维环境映射到二维平面上，这种映射方式要用成像变换来描述，即摄像机成像模型。以下介绍图像坐标系、相机坐标系、世界坐标系三者之间的转化。

图1　图像坐标系

图1中，(u,v)轴表示以像素为单位的像素坐标系，(X,Y)表示以“mm”为单位的图像坐标系。在(X,Y)坐标系中，原点O1定义在摄像机光轴和图像平面的交点，位于图像中心处。若O1在u、v轴坐标系中的坐标为(u0,v0)，每一个像素在X轴与Y轴方向上的物理尺寸为dX、dY，则图像中任意一点的像素坐标与图像坐标转换关系如下：

(1)

转换为齐次坐标形式：

(2)

由像素坐标表示图像坐标：

(3)

在实践中，摄像机可安放在环境中的任意位置，可任意选择一个基准坐标系描述环境中所有物体的位置，同时也可表示摄像机的位置，该坐标系称为世界坐标系。其坐标轴由XW、YW、ZW表示。图2表示摄像机的成像模型。

图2　摄像机坐标系与世界坐标系

图2中O点是光学中心，光轴和所成图像平面的交点O1一般在图像的正中心，在这里是图像坐标的原点，OO1为摄像机焦距[1]。x轴和y轴与图像的X轴与Y轴平行，Z轴为摄像机光轴，垂直于图像平面。由点O与x，y，z轴构成的直角坐标系称为像机坐标系。

摄像机坐标系与世界坐标系之间的变换关系，可以用选择旋转矩阵R和平移向量t来建立[1]。则摄像机坐标系下的齐次坐标[Xc,Yc,Zc,1]T与空间中任意一点P在世界坐标系下的齐次坐标[Xw,Yw,Zw,1]T可通过如下关系来转换：

(4)

式中，R为3×3旋转矩阵，同时也是单位正交矩阵；t为三维平移向量；0=[0,0,0]T；M1为4×4矩阵。

1.2摄像机线性模型(针孔模型)摄像机线性模型也叫做针孔成像模型[4-5]。空间任意点P在图像上的投影位置P是光心O与P点的连线OP与图像平面的交点，根据坐标比例模型，有如下关系：

(5)

式中，(x,y)为p点的图像物理坐标；(Xc,Yc,Zc)为空间点P的摄像机坐标，这种关系也成为称为中心摄影或透视摄影，根据这一关系空间中任意一点P的图像坐标可用针孔模型近似表示。利用齐次坐标与矩阵形式表示此透视投影关系：

(6)

将式(3)、式(4)与式(6)合并，得到P点的世界坐标(Xw,Yw,Zw)与其投影点p的图像像素坐标(u,v)之间的关系：

=MXw

(7)

式中，ax=f/dx，ay=f/dy，Xw=[Xw,Yw,Zw]T；M为3×4的投影矩阵，M1由相机内参决定，M2由相机外参决定。

1.3标定原理摄像机标定是指建立摄像机图像像素位置与点场景位置之间的关系，主要是根据摄像机模型，选取已知特征点的图像坐标和世界坐标[6]，来求解摄像机的模型参数，也就是上一节提到的内参和外参，如表1所示。

表1　摄像机模型内参外参

表1表达式中，ax、ay、u0、v0、γ是线性模型的内部参数，ax、ay分别为u轴和v轴的尺度因子，或称为有效焦距，与式(2)对比可得ax=f/dx,ay=f/dy，dx、dy分别为水平方向与竖直方向的相邻两像素点之间的间距，u0、v0是光学中心，γ是u轴和v轴不垂直因子(一般为0)内参与摄像机的内部结构有关；R和T是旋转矩阵和平移矩阵，称为外部参数，由摄像机相对于世界坐标系的位置决定。在非线性模型中，内部参数除了线性模型的ax，αy，u0，v0,γ外，还包括径向畸变参数k1,k2切向畸变参数p1和p2[7]。

根据已知的参照物求投影M矩阵，当作其余算法的参照数据。可将式(7) 中的M矩阵改写成下式：

(8)

式中，(Xwi,Ywi,Zwi,1)T为场景中第i个已知参照点的世界坐标；(ui,vi,1)为i个点的图像像素坐标；mij为投影矩阵中位于第i行j列元素，式(8)可列为以下方程组：

(9)

将M矩阵分解， 式(2)～(7)的M矩阵与摄像机的内外参数如下：

(10)

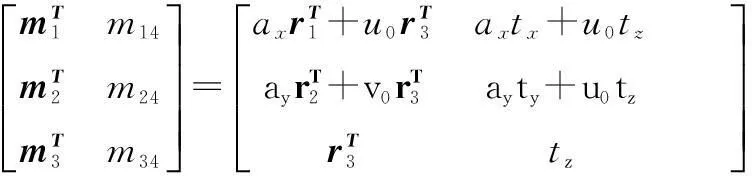
(11)

依次计算得到r3、u0、v0、ax及ay：

r3=m34m3

(12)

(13)

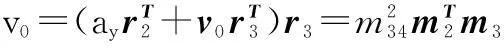
(14)

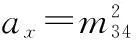
(15)

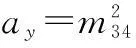
(16)

进一步求出以下参数：

(17)

(18)

tz=m34

(19)

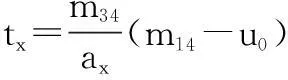
(20)

(21)

综上所述，场景中最少6个点的世界坐标点以及相对应的像素坐标点可以求出M矩阵，并根据式(12)～(21) 依次确定摄像机的内外参数。

2果蔬位姿深度信息恢复试验

2.1双目平行相机模型人们早就认识到，双眼观察物体时会有立体感，双目平行相机模型就是模仿这一视觉机理，通过对同一物体在左右图像上投影的视差，根据几何比例模型来计算该物体在场景中的坐标。如图3所示视差原理，左相机和右相机的光学中心分别设为Cl和Cr，目标点P在两相机图像上的投影点分别为Pl和Pr，相机距离为b，焦距为f。P与ClCr的连线距离为d，过C1、Cr分别向图像平面作垂线C1A1、CrAr，过点P向图像平面作垂线PB。令|AlPl|=la，|ArPr|=lb,|PrB|=a。

图3　视差测距原理

按照三角形相似原理得出：

(22)

解得：

(23)

假设C1、C2分别为两相机的位置，则在三维空间的坐标分别为O1x1y1z1、O2x2y2zz，则在上述摄像机配置下，若任何空间P1点的坐标在C1坐标系下为(x1,y1,z1)，C2在坐标系下为(x1-b,y1,z1)。由中心摄影的比例关系可得：

(24)

(25)

其中(u1,v1)、(u2,v2)分别为p1与p2的图像坐标。在图3所示的简单摄像机配置下，假设Cl坐标系就是世界坐标系的情况下，可得：

(26)

可见，由p1与p2的图像坐标(u2，v2)，(u2,v2)可求出空间点P的三维坐标(x1,y1,z1)。同理可得出以另一个相机为基准的空间坐标。

图4　基线长度的讨论

2.2基线长度的选取调整双目摄像机的过程中，要注意2个摄像头在同一高度，2个镜头保持同一平面，以保证2个相机光轴平行。摄像机使其在试验过程中不受干扰。在调整两摄像机距离的过程中，需考虑以下问题：

(1) 双目摄像机由于平行放置而很有可能导致2幅图的共同特征点不能匹配。一种可能是由于两相机的视差太大或在测量目标元素距离太近时，导致两相机共同视野下不存在目标元素，只可在一个相机中成像；第二种可能是由于拍摄环境较为复杂，目标元素被其他物体遮挡下只可在其中一个相机中有投影。以上情况导致特征点在两幅图上找不到相互的对应性。解决方法只能减小相机距离，如图4所示阴影部分为共同可视部分，随着a的长度减小，可使其共同视野增加，出现上述情况的概率也随之减小。

(2)虽然上述方法解决了视野问题，但随之带来的就是精确度问题。若一味地减小相机距离，当像机间隔趋近0时，虽不存在视野问题，但是双目也就失去了意义。随着基线长度增加，可减小2幅图匹配后视差的相对误差，将增加深度测量的精度，而共同视野及匹配的概率也随之降低。

总而言之，基线长度的选取要充分考虑拍摄对象的大小和拍摄距离。

2.3豆角坐标定位考虑到豆角的长宽相对较小，拍摄距离相比豆角的实际大小相对较远，为了提高结果的准确性，基线长度选定为200 mm。

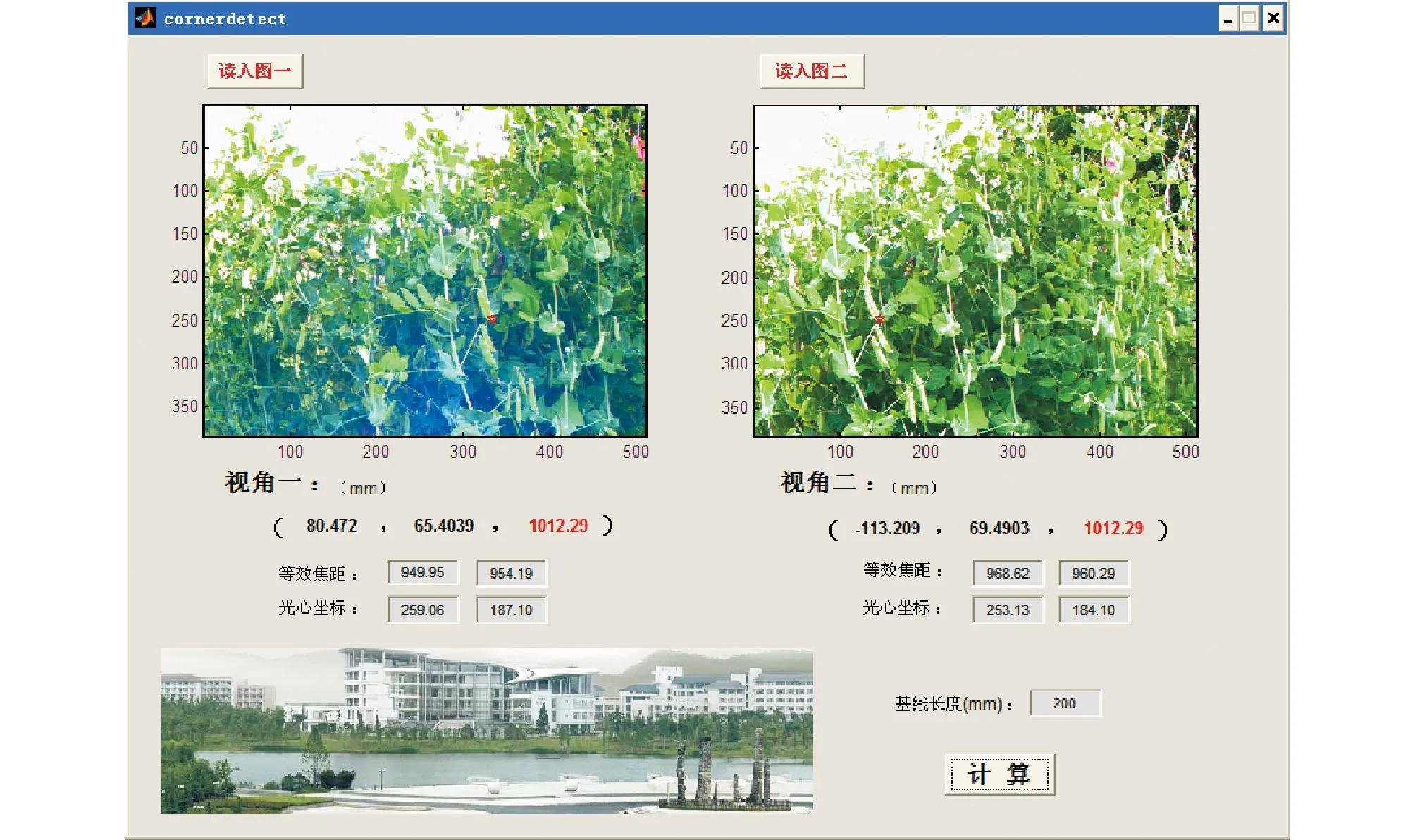
图5　豆角位姿坐标定位结果

根据标定结果，分别依次输入2个摄像机的内外参数，读入左右图片(2幅图尽可能保证在同一帧下拍摄，注意分辨率要与标定时一致)，再对同一目标分别在左右图片上点选取特征点，计算2幅图的相机坐标系。计算结果见图5。针对豆角不同距离进行定位测试，将实际距离与测试距离比较，测试结果见表2。

表2　豆角位姿恢复试验测试结果

由表2可知，当测试距离较近时，由于左右图像上同一目标的横向坐标相差交大，取点匹配后相对误差较小，距离的计算结果较为精确。但随着测试距离增加，同一目标点在左右图像上的坐标变化不再明显，这为取点匹配带来一定困难，误差随之增大。事实上，随着测试距离变为无限远，双目就失去了意义。

3结论

利用双目平行相机模型，可以对三维场景进行模拟，但是人工调节下设备难以达到理想效果，并且需考虑实际拍摄物的远近、大小来适当调整。如果需要进一步精确，还需要对拍摄图像进行畸变处理。

智能化的发展对特征点自动提取和立体匹配的需求越来越强烈，但是自动提取需要在应对不同拍摄环境下需针对性处理，尤其是复杂的场景中特征点的提取难度也随之增加。因此，优化算法以应对实际生产生活中的诸多不确定因素，仍是双目立体观赏信息获取技术改进的方向。

参考文献

[1] 马颂德,张正友. 计算机视觉:计算理论与算法基础[M].北京：科学出版社,1998.

[2] 崔岩.基于双目立体视觉的距离测量[D].长春：长春理工大学,2007.

[3] 田国会,李晓磊,赵守鹏,等.家庭服务机器人智能空间技术研究与进展[J].山东大学学报(工学版),2007,37(5):53-59.

[4] 徐冠华,田国良,王超,等.遥感信息科学的进展和展望[J].地理学报,1996,51(5):385-397.

[5] 马玉真,胡亮,方志强,等.计算机视觉检测技术的发展及应用研究[J].济南大学学报 (自然科学版),2004,18(3)：222-227.

[6] 乔毅.移动机器人双目视觉的三维重构[D].哈尔滨：哈尔滨工程大学,2007.

[7] 徐杰.机器视觉中摄像机标定 Tsai 两步法的分析与改进[J].计算机工程与科学,2010,32(4):45-48.

收稿日期2015-11-20

作者简介乔方博(1991- )，男，山西大同人，硕士研究生，研究方向：智能机器人、农林业信息监测等。*通讯作者，讲师，博士，从事农林业信息监测、智能机器人控制技术等研究。

基金项目国家自然科学基金项目(61302185,31300539)；浙江省自然科学基金项目(LQ14F030014，LQ13F030012)；浙江省林业智能监测与信息技术研究重点实验室开放基金项目；浙江农林大学智慧农林业研究中心预研项目(2013ZHNL03)；浙江农林大学人才启动基金项目(2013FR023，2013FR085)。

中图分类号S 126

文献标识码A

文章编号0517-6611(2015)36-374-05