软集与模糊集的格

柳晓燕

(西安邮电大学 理学院, 陕西 西安 710121)

软集与模糊集的格

柳晓燕

(西安邮电大学 理学院, 陕西 西安 710121)

从格论角度研究软集的一些代数性质，证明了给定论域上的全体软集可构成正交模格及布尔代数等格结构。依此指出给定论域上全体模糊集的格可嵌入全体软集的格，基于格论刻画了软集与模糊集之间的内在联系。

软集；模糊集；格；布尔代数；正交模格

随着物联网、云计算、移动互联网和电子商务等信息科学技术的广泛应用，人类社会正飞速迈入信息化时代，每时每刻各种纷繁复杂的数据不断涌现，数据的重要意义和潜在价值获得了前所未有的重视。与此同时，人们发现诸如工程技术、环境科学、生物医药和认知科学等领域内的大量实际问题均涉及挖掘、分析和处理各种各样的不确定性数据，这些数据中内蕴的不确定性和复杂性使得一些经典数学工具不能直接应用。为应对实际应用中的新挑战，数学、信息和控制领域的研究者相继提出了若干处理不确定性的理论和方法，包括模糊集、粗糙集、Flou集、Vague集、灰色理论和置信理论等。其中模糊集和粗糙集分别体现了处理不确定性的程度化和粒度化的重要思想，已被广泛应用到数据挖掘、机器学习、近似推理、专家系统、决策分析、模式识别和聚类分析等领域。

软集理论[1]从参数化的崭新角度提供了表示和处理不确定性的一种新思路。软集给定论域的参数化的子集族，利用参数标记并组织论域中的元素，进而形成一定的结构并应用于不确定问题的建模及分析。在一定意义下模糊集和粗糙集均可看作软集的特例[2]。软集定义中既涉及对象集，又引入了参数空间，相对于模糊集、粗糙集等不确定计算理论而言，能够进行更为丰富的信息描述和处理，已应用于博弈论、运筹学、Perron积分、概率论及测度论等方面[3]。近年来，国际上关于软集的研究进入了十分活跃的阶段[4-10]。

计算机科学中广泛关注的布尔代数[11,12]是经典二值逻辑对应的代数结构，而正交模格是量子逻辑对应的代数结构，随着量子信息与量子计算方面研究的快速发展，正交模格已成为量子信息与量子计算中最重要的量子结构之一。本文将从格论角度研究给定论域上全体软集形成的格结构，并讨论软集与模糊集的格结构之间的内在联系。

1 软集与模糊集

给出关于软集与模糊集的一些基本概念和命题，并指出两者之间的内在关系。令U是一个非空集合，称为论域。记U的所有子集构成的类为P(U)。

定义1[1]设E是给定集合(称为参数域)，序对(F,A)称为论域U上的一个软集，其中A⊂E，F∶A→P(U)是一个映射。

对软集(F,A)，称A为其参数集，并称F∶A→P(U)为它的参数化映射。根据上述定义，论域U上的一个软集可看作U上的一个参数化的子集族。为了便于对上述概念有一个直观的认识，给出下面的例子。

例 设有8种Web搜索应用构成的论域U={x1,x2,…,x8}。可从不同角度对这些应用进行评价，例如响应时间短(a1)，搜索精度高(a2)，报错率低(a3)等。记A={a1,a2,a3}，则A构成参数集。定义映射F∶A→P(U)为F(a1)={x1,x2,x5,x7}，F(a2)={x3,x5,x6,x8},F(a2)={x4,x5,x8}则(F,A)就是U上的一个软集，它从不同侧面给出这些Web搜索应用的信息描述。易见本例中应用x5具有最佳性能。

下面的两个定义对文献[10]中相关的定义作了简单的修正，从后面的讨论中可以看出所作修正的合理性及必要性。

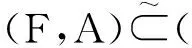
(1)A⊂B；

(2) ∀x∈A，F(x)⊂G(x)。

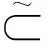
定义3 设(F,A)和(G,B)是论域U上的软集，则(F,A)和(G,B)的交(F，A)(G,B)是U上的一个软集(H,C)，其中C=A∩B；H∶C→P(U)定义为H(x)=F(x)∩G(x),x∈C。通常也将映射H记为

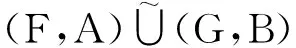
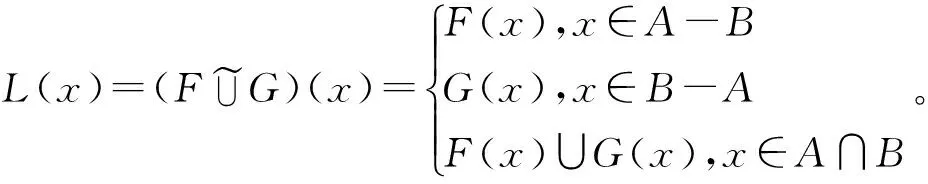
定义5 设(F,A)是U上的软集，则(F,A)的补(F,A)c定义为U上的软集(M,A)，其中映射M∶A→P(U)定义为

M(x)=F(x)c=U-F(x),x∈A。

通常也将映射M记为Fc。

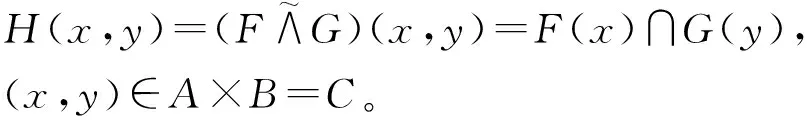
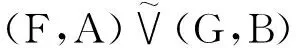
以下关于模糊集的一些基本概念，指出软集和模糊集之间的联系。论域U到单位区间I=[0,1]的映射μ∶U→[0,1]称为U上的一个模糊集。对x∈U，称μ(x)为x对μ的隶属度，它反映了论域中元素x对于模糊集μ的从属程度。特别的，μ(x)=1表示全隶属，而μ(x)=0表示不隶属。论域U上所有模糊集构成的类记为F(U)。

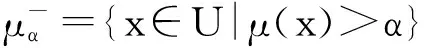
定义9 设μ,v∈F(U)，若对任意x∈U有μ(x)≤v(x)，则称μ包含于v(或v包含μ)，并记为μ⊂v(或v⊃μ)。若μ⊂v且v⊃μ，则称μ和v相等，记为μ=v。

定义10 设μ,v∈F(U)，定义U上的模糊集μ∪v，μ∩v为

(μ∪v)(x)=μ(x)∪v(x),(μ∩v)(x)=μ(x)∩v(x),x∈U

分别称μ∪v和μ∩v为μ和v的并与交。

定义11 设μ∈F(U)，对任意x∈U，令μc(x)=1-μ(x)，则μc是U上的模糊集，称为μ的补。

若(D,∨,∧,′,0,1)是一个有界分配格，并且满足对合律及De Morgan律，即对任意x,y∈D，有x″=x,(x∨y)′=x′∧y′和(x∧y)′=x′∨y′成立，则(D,∨,∧,′,0,1)称为一个De Morgan代数。

若将U的普通子集A和其特征函数χA等同起来，则可认为Φ(即χΦ)和U(即χU)分别是(F(U),⊂)中的最小元和最大元。事实上，可以证明关于模糊集类F(U)的如下结果。

定理1[4](F(U),∪,∩,c,Φ,U)是一个De Morgan代数。

命题1 设μ∈F(U)，则对任意x∈U，有μ(x)=sup{α∈[0,1]|x∈μα}。

证明 任取x∈U，令A={α∈[0,1]|x∈μα}。对任意α∈A，由x∈μα知μ(x)≥α，故μ(x)是A的一个上界。又取α0=μ(x)，则α0∈[0,1]且x∈μα0，故α0=μ(x)∈A。综上可得μ(x)是A的上确界，即μ(x)=sup{α∈[0,1]|x∈μα}。

给定论域U上的一个模糊集μ，通过求α-截集，可以得到U的一个子集族{μα|α∈[0,1]}。另一方面，上述命题表明，由α-截集构成的族，可以重构出原来的模糊集。由此可得如下结论。

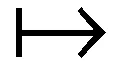
2 软集的格

论域U上的模糊集类F(U)关于模糊集的并、交及补运算构成一个De Morgan代数。取定参数集A，记论域U上以A为参数集的全体软集构成的类为S(A,U)，讨论软集类S(A,U)的性质及结构。

取定参数集A后，软集的一些相关概念将得到简化。例如对(F,A),(G,A)∈S(A,U)，由定义得

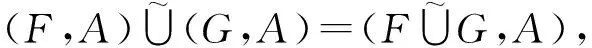
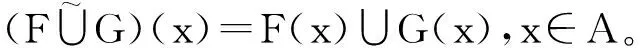
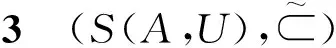
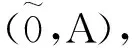
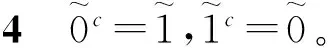
证明 对任意x∈A，有

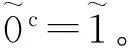
命题5 设(F,A)∈S(A,U)，则((F,A)c)c=(F,A)，即软集的补运算满足对合律。

证明 设((F,A)c)c=(G,A)，对任意x∈A，由定义可知

G(x)=(Fc(x))c=U-(F(x))c=F(x)，

于是G=F，从而有(F,A)=(G,A)，即

((F,A)c)c=(G,A)。

命题6 设(F,A),(G,A)∈S(A,V)，则下列等式成立

即软集关于并、交及补运算满足De Morgan律。

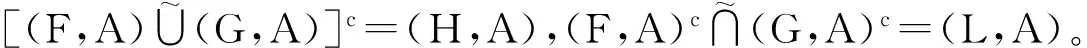
[F(x)∪G(x)]c=(F(x))c∩(G(x))c

另一方面，有

于是H=L，故(H,A)=(L,A)，即

对偶地，可证等式(DM2)成立。

命题7 设

(F,A),(G,A),(H,A)∈S(A,V)，

则下列等式成立。

(L1) 交换律

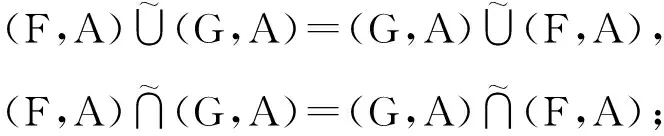
(L2) 结合律

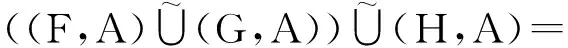
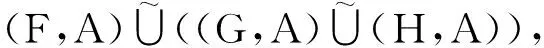
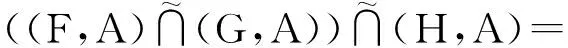
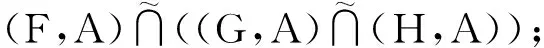
(L3) 幂等律

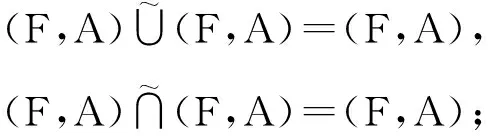
(L4) 吸收律

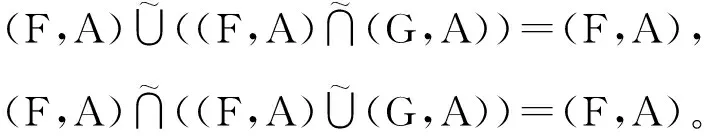
证明 仅证每组的第一个等式成立，另一个的证明是类似的。

(L1) 设

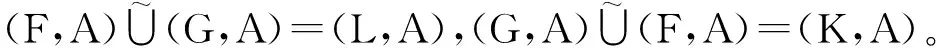
对任意x∈A，有

F(x)∪G(x)=G(x)∪F(x)=

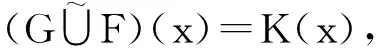
故(L,A)=(K,A)，即

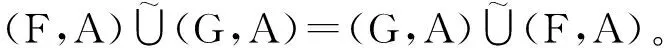
(L2) 设

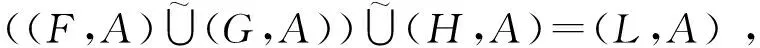
对任意x∈A，有

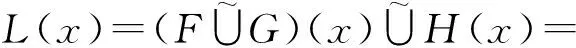
(F(x)∪G(x))∪H(x)。

另一方面，

F(x)∪(G(x)∪H(x))，

则L=K。因此(L,A)=(K,A)，即

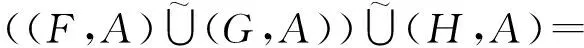
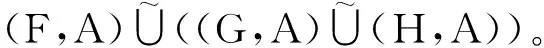
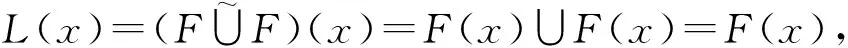
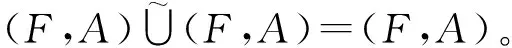
(L4) 设

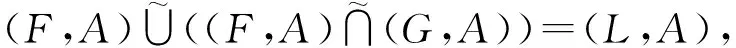
F(x)∪(F(x)∩G(x))=F(x),

于是(L,A)=(F,A)，即

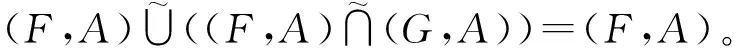
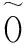
命题8 设

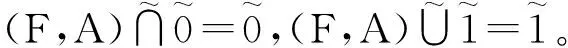
命题9 设

(F,A),(G,A),(H,A)∈S(A,U),

则下列等式成立

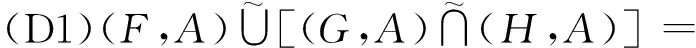
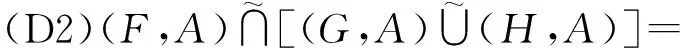
即软集的并、交运算满足分配律。

证明 下面仅证明等式(D1)成立。设

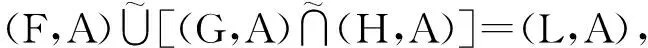
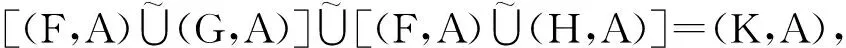
则对任意x∈A，有

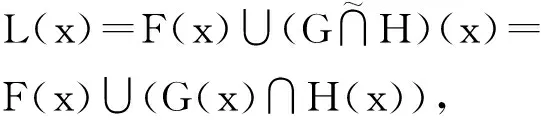
而

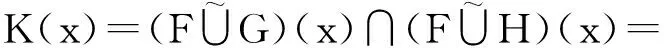
[F(x)∪G(x)]∩[F(x)∪H(x)]，

故(L,A)=(K,A)，即等式(D1)成立。类似地，可以证明等式(D2)成立。

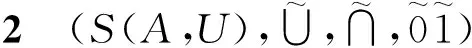
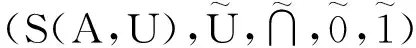
构成一个De Morgan代数。

命题10 设(F,A)∈S(A,U)，则下列等式成立

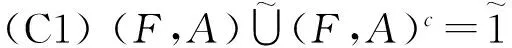
即软集关于并、交和补运算满足补余律。

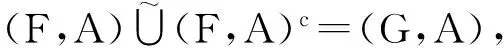
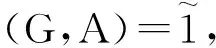
根据格论中的相关知识，可知一个格可以看成是一个代数系统，同时也可视为一个偏序集。如前所述，软集类S(A,U)关于软包含关系构成一个偏序集，而它关于并和交运算又是一个分配格。这两方面可由如下命题联系起来。

命题11 设(F,A),(G,A)∈S(A,U)，则下列条件等价

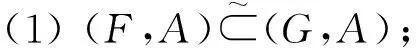
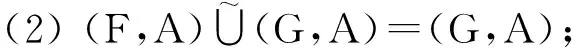
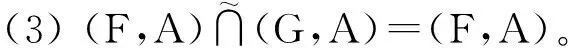
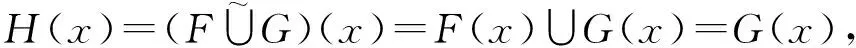
故(H,A)=(G,A)，即

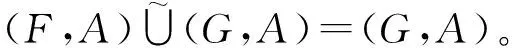
定义12[11]一个(2,2,1,0,0)-型代数(L,∨,∧,′,0,1)称为正交格，若它满足下列条件：

(Q1) (L,∨,∧,0,1)是一个有界格；

(Q2) 对任意x∈L，有x∨x′=1和x∧x′=0；

(Q3) 对任意x,y∈L，有(x∨y)′=x′∧y′和(x∧y)′=x′∨y′；

(Q4) 对任意x∈L，有(x′)′=x。

由定理2和命题10，可得如下结论。

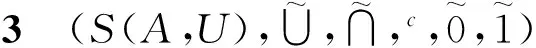
定义13[11]一个正交格(L,∨,∧,′,0,1)称为正交模格，若它满足

(Q5) 对任意x,y∈L，有

x≤y⟹x∨(x′∧y)=y。

定义14[11]一个格(L,∨,∧)称为模格，若它满足称为模律的条件

(M) 对任意x,y,z∈L，有

x≤y⟹x∨(y∧z)=y∧(x∨z)。

命题12[11]分配格是模格。

由定理3和命题12，可证软集类构成一个正交模格。

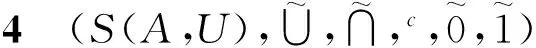
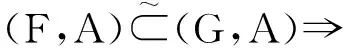
即条件(Q5)成立。事实上，设

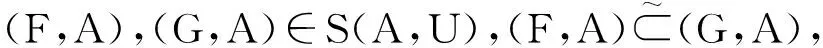
由命题12知格S(A,U)满足模律，那么有

故格S(A,U)满足条件(Q5)。

若有界分配格(B,∨,∧,′,0,1)满足补余律，即对任意x∈B，有x∨x′=1和x∧x′=0，则称(B∨,∧,′,0,1)为布尔代数[11]。

由前已证，可得如下结论。

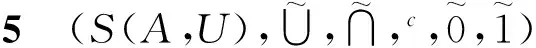
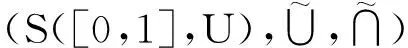
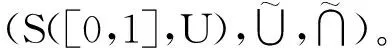
证明 作映射

其中参数化映射Fμ∶[0,1]→P(U)定义为

Fμ(α)=μα={x∈U|μ(x)≥α}，α∈[0,1]。

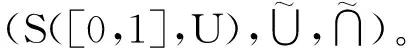
(1)Ψ是格同态。即证对任意μ,v∈F(u)，有

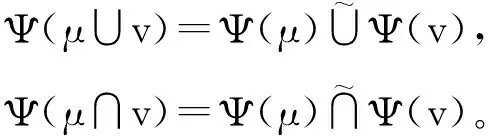
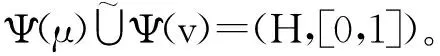
另一方面，有

Fμ∪v(α)=(μ∪v)α=

{x∈U|(μ∪v)(x)≥α}=

{x∈U|μ(x)∨v(x)≥α}

易见

μα∪vα={x∈U|μ(x)∨v(x)≥α},

故H=Fμ∪v。于是有

Ψ(μ∪v)=(Fμ∪v,[0,1])=

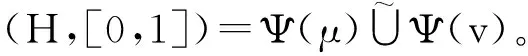
类似地，可以证明

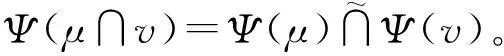
(2) Ψ是单射。设μ,v∈F(U)，使得

Ψ(μ)=Ψ(v)。

下面证明μ=v。事实上，由Fμ=Fv，可知对任意α∈[0,1]，均有μα=Fμ(α)=Fv(α)=vα。那么，任取x∈U，由命题1得

μ(x)=sup{α∈[0,1]|x∈μα}=

sup{α∈[0,1]|x∈vα}=v(x)，

因此μ=v。

3 结束语

证明了给定论域上的全体软集可构成正交模格和布尔代数，指出了给定论域上全体模糊集构成的格可嵌入到全体软集构成的格，从格论的角度刻画了软集与模糊集之间的内在联系。与软集相关的其它格结构及其在软计算、数据挖掘和决策分析等领域中的应用有待于研究。

[1]MolodtsovD.Softsettheory-firstresults[J].ComputMathAppl, 1999(37): 19-31.

[2]AktaH, ÇN.Softsetsandsoftgroups[J].InformationSciences, 2007(177): 2726-2735.

[3]MolodtsovD.TheTheoryofSoftSets[M].Moscow:URSSPublishers, 2004.

[4] 代建华. 粗代数与三值Lukasiewicz代数[J]. 计算机学报, 2007, 30(2): 161-167.

[5]FengF,LiuXY,Leoreanu-FoteaV,etal.Softsetsandsoftroughsets[J].InformationSciences, 2011 , 181 (6), 1125-1137.

[6]LiuXY,FengF,ZhangH.Onsomenonclassicalalgebraicpropertiesofinterval-valuedfuzzysoftsets[J/OL].[2014-09-20].http://www.hindawi.com/journals/tswj/2014/192957.

[7]FengF,LiYM.Softsubsetsandsoftproductoperations[J].InformationSciences, 2013(232): 44-57.

[8]LiuXY,FengF,JunYB.Anoteongeneralizedsoftequalrelations[J].ComputMathAppl, 2012(64): 572-578.

[9]AkramM,DavvazB,FengF.IntuitionisticfuzzysoftK-algebras[J].MathematicsinComputerScience, 2013(7): 353-365.

[10]FengF,AkramM,DavvazB,etal.Attributeanalysisofinformationsystemsbasedonelementarysoftimplications[J].Knowledge-BasedSystems, 2014(70): 281-292.

[11]BurrisS,SankappanavarHP.ACourseinUniversalAlgebra[M].Berlin:Springer, 1981.

[12]YingMS.Atheoryofcomputationbasedonquantumlogic(I)[J].TheoretComputSeiences, 2005(344): 134-207.

[责任编辑：祝剑]

On lattices of soft sets and fuzzy sets

LIU Xiaoyan

(School of Science, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

Some algebraic properties of soft sets are investigated in this paper from a lattice-theoretical point of view. It is shown that the class of all soft sets over a given universe can form lattice structures including orthomodular lattices and Boolean algebras. In addition, it is pointed out that the lattice of fuzzy sets can be embedded into the lattice of soft sets, which characterizes some inner connections between soft sets and fuzzy sets based on lattice theory.

soft sets, fuzzy sets, lattices, Boolean algebras, orthomodular lattices

10.13682/j.issn.2095-6533.2015.04.016

2014-10-22

国家自然科学基金资助项目(11301415)；陕西省青年科技新星计划资助项目(2014KJXX-73)

柳晓燕(1980-)，女，硕士，讲师，从事软计算、数据挖掘等研究。E-mail: lxy031010@163.com

TP18

A

2095-6533(2015)04-0074-06