一种基于编码的数字签名算法的改进
任 方, 郑 东
(1. 西安邮电大学 通信与信息工程学院, 陕西 西安 710121;2. 西安邮电大学 无线网络安全技术国家工程实验室, 陕西 西安 710121)
一种基于编码的数字签名算法的改进
任 方1,2, 郑 东2
(1. 西安邮电大学 通信与信息工程学院, 陕西 西安 710121;2. 西安邮电大学 无线网络安全技术国家工程实验室, 陕西 西安 710121)
为提高基于编码的数字签名算法CFS的效率,利用基于编码的Hash函数对其进行改进。引入一个Hash函数,其输出是一个重量不超过码的纠错能力t的正则字的校验子,用该函数替换原CFS算法中使用的随机Hash函数,使签名过程中译码算法只需执行一次,从而避免多次尝试带来的时间消耗。改进算法的签名时间比原始算法缩短了t!倍,签名效率摆脱了码的纠错能力的限制,且二者的安全性依赖于等价的NP完全问题。
数字签名;编码;校验子;Hash函数;量子攻击
基于编码的公钥密码技术是目前公认的可以抵抗量子攻击的公钥密码技术[1-2],是公钥密码学未来发展的主流之一。基于编码的公钥加密算法最早由McEliece提出[3],该算法基于二元不可约Goppa码,加密过程等价于给明文码字添加一个随机选择的错误向量,而解密相当于译码。McEliece算法的安全性可以有效归约到两个NP完全问题:二元随机码的译码问题以及Goppa码和随机码的区分问题[4-5]。其后出现的Niederreiter算法[6]的安全性被证明与McEliece算法等价。编码密码技术诞生以来产生了大量的研究成果,包括加密、数字签名[7-8]、认证[9]、Hash函数[10]、流密码[11]等,其中的Courtois-Finiasz-Sendrier(CFS)签名算法[7]已经成为该领域的经典算法。
CFS算法是第一个安全的基于编码的签名算法,它是一种基于二元Goppa码的签名算法,由Niederreiter加密算法改造而来。对于CFS的安全性已经有了充分的讨论[12-13],各种改进算法如mCFS[13]和并行CFS[14]等也相继出现,此外基于CFS可以用来构建其它特殊用途的签名如环签名[15-16]和盲签名[17]等。所有这些签名算法的核心都与CFS一致,即签名时对消息的Hash值进行处理使其成为一个Goppa码的校验子,签名过程是利用秘密的译码算法对该校验子进行译码,将码字作为签名值,而验证签名时通过计算码字的校验子并与消息的Hash值进行对比来检验签名的有效性。
CFS系列签名算法都有较高的安全性,但其缺陷也是明显的,即签名效率很低。以基本CFS算法为例,要得到一个可以译码的校验子,平均需要进行t!次尝试,其中t是所使用的Goppa码的纠错能力。显然随着t的增加,签名时间将会呈指数迅速增长,而较小的t值又会带来安全性低的缺陷,同时与纠错码追求较强的纠错能力成为矛盾,这在一定程度上阻碍了CFS系列算法的应用。
本文针对CFS算法的这一缺陷,通过分析算法的实现细节,寻找签名效率低下的主要原因,并对算法的签名过程进行改进,使其签名时间不随参数t的增加而迅速增长。
1 基础知识
1.1 纠错码
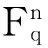
定义2 一个(n,k)线性分组码C的生成矩阵是一个k×n的矩阵G,其中G的行向量构成了C的一组基。
线性分组码C的生成矩阵G不唯一,但是不同的生成矩阵可以通过初等行变换相互转化,即若G是C的一个生成矩阵,P是一个初等矩阵,则PG也是C的一个生成矩阵。
定义3 一个(n,k)线性分组码C的校验矩阵是一个(n-k)×n的矩阵H,其中H的任意行向量与C的生成矩阵G的任意行向量正交,即HGT=0。
线性分组码的校验矩阵不唯一且可以通过初等行变换相互转化。长为n的向量c是C的一个码字的充分必要条件是HcT=0。对于任意的字c,将HcT称为c的校验子。
定义4 线性分组码的两个码字
u=(u1,u2,…,un),v=(v1,v2,…,vn)
的Hamming距离d(u,v)定义为u和v的不同分量的个数,即
d(u,v)=|{i:ui≠vi}|,
码字u的Hamming重量w(u)定义为u与全0码字0的距离,即
w(u)=d(u,0),
码C的非零码字的最小Hamming重量称为C的最小距离,一般记作dmin。
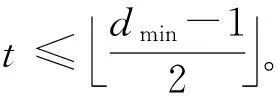
Goppa码是一种特殊的线性分组码,McEliece加密算法使用的Goppa码的参数满足
n=2m, k=n-mt。
利用Goppa码的具体结构知识可以进行有效的译码,这也是构造基于编码的密码算法的基础。即将Goppa码的结构作为秘密的陷门信息,或者解密私钥,可以实现单向陷门函数,从而构造公钥加密与签名算法。
以下只讨论F2上的线性分组码与Goppa码。
1.2 困难问题
基于编码的公钥密码算法主要依赖于一些困难问题,它们均已被证明是NP完全问题,可以有效抵抗目前已知的量子攻击。
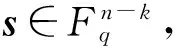
Goppa码的区分(Goppa Code Distinguishing,GD)问题 输入有限域Fq上的一个(n-k)×n的矩阵H,问H是一个(n,k) Goppa码的校验矩阵还是一个随机(n,k)码的校验矩阵?
2 CFS签名算法及其分析
2.1 CFS签名算法
构造数字签名算法一般有三种方法:一是利用现有的公钥加密算法;二是利用现有的身份认证算法;三是直接构造。CFS签名算法属于第一种,它是基于Niederreiter加密算法构造的签名算法。此类算法签名过程的模式一般为
(1) 使用公开的Hash函数计算待签名消息的Hash值。
(2) 将这个Hash值看做加密算法的密文,用私钥进行解密。
(3) 将这一解密结果附加在消息后作为签名值。
对于基于编码的签名算法,上述步骤的第二步往往不可行,原因在于Niederreiter算法输出的密文是错误向量的校验子,该校验子未必一定是可以译码的。只有那些重量不超出所选Goppa码的译码能力t的错误向量的校验子才是可以译码的,因此CFS算法是一种概率签名算法。
详细的CFS算法描述如下。
(1) 参数生成
•随机选择一个F2上的(n,k) Goppa码C,纠错能力为t,校验矩阵为H,以及有效的校验子译码算法γ。
•随机选择一个F2上的(n-k)×(n-k)的可逆矩阵Q,一个n×n的置换矩阵P。
•选择一个公开的安全Hash函数
•系统公开参数为〈h,t,Hpub=QHP〉,私钥为〈Q,H,P,γ〉。
(2) 签名过程
设签名者需要签署的消息为m。
•计算消息的Hash值s=h(m)。
•对于i=0,1,2,…,将其转换为二进制向量I,计算si=Q-1h(s‖I),找到使得γ(si)存在的最小的i,记作i0。
•记ν=γ(si0),则签名值为(I0‖νP)。
(3) 验证过程
设验证者收到的消息签名对为〈m,I‖u〉。
•计算a=h(h(m)‖I),以及b=HpubuT。
•若a=b则签名正确,否则签名验证失败。
2.2 对CFS签名算法的分析
CFS算法的安全性已经获得严格的形式化证明[13],并在随机预言机模型下被归约到SD问题和GD问题上。由于具备了较高的安全性,目前大多数基于编码的签名方案均基于CFS进行构造。
尽管CFS算法有很高的安全性,但其实现效率即签名的速度却比较低,这主要是因为进行签名时需要进行多次译码尝试。
对于选定的(n=2m,k=n-mt) Goppa码,设可以有效译码的校验子个数为Nd,总的校验子个数为Nt,显然有
因此CFS算法签名成功的概率为
即平均需要尝试t!次才能够得到一个可以译码的校验子。随着t的增长,这一数字增长非常快,如果取t=9,则平均需要尝试9!=362880次才能得到一个签名[7],但是在相关攻击下这一参数已经不再安全[12]。建议参数需要取
m=15,t=12,
或者
m=16,t=10。
从长远来看,随着新的攻击方法的出现,t的取值要求必然越来越大,这就使得签名成功的次数呈指数增长,签名速度会越来越低,算法的实现效率也会越来越差。
造成CFS算法签名效率低下的主要原因是由消息的Hash值计算出的si一般不是码C的可以译码的校验子,从而要多次计算不同的si去尝试译码,只有当某个si恰好在C的译码能力之内,译码才能完成,签名也才能成功。为了提高签名效率,需要对算法进行改进,使得计算出的si本身一定或者至少以很大的概率是可译码的校验子。
3 基于编码的数字签名算法改进
首先构造基于编码的Hash函数,以此对CFS签名算法进行改进。
3.1 基于编码的Hash函数
基于编码的Hash函数构造方法,最早只是基于一个压缩函数f对给定消息进行多轮循环计算,最终得到消息的Hash值。可以证明按照这种方法构造出的Hash函数安全性不低于压缩函数的安全性[10]。
设压缩函数f的输入为e位,输出为r(r (1) 在第一轮,先选择长度为r的初始向量vI,再从给定消息中选取e-r位,与vI连接组成长为e的向量,作为函数f的输入,得到r位的输出。 (2) 从第二轮开始,每轮迭代将前一轮r位的输出反馈回输入端,再从给定消息中选取e-r位,共同组成长为e的向量作为f的输入,计算新的r位输出。 (3) 循环这一过程直至消息位被取完,最后一轮当消息剩余位数不足e-r位时,随机选择若干比特进行填充,使其满足输入位数要求。将函数f的最后一轮输出作为消息的Hash值。 上述迭代过程可参看图1。 图1 Hash迭代过程 Hash函数的构造中,最核心的部分是压缩函数f。以下给出一种基于编码困难问题的压缩函数f的构造方法。 选择一个(n,k) Goppa码,其中 n=2m,k=n-mt, 选择正整数w|n,显然有 w=2m′(m′ 另取 则可以将长度为n的每一个字分成等长的w个块,每一块包含l个比特。如果一个重量为w的字c在每一个块((i-1)l,il](i=1,2,…,w)内恰好有一个1,则称c为正则字。 所选Goppa码的校验矩阵是一个(n-k)×n的矩阵H,可以将H分成w个子矩阵,即 H=(H1,H2,…,Hw), 其中每一个子矩阵 Hi=(hj) (i=1,2,…,w;j=(i-1)l+1, (i-1)l+2,…,il), 而hj为矩阵H的第j列。 定义压缩函数 x=(x1,x2,…,xw), 则函数的输出 f(x)=z。 定理1 上述压缩函数f的输出等价于计算一个长为n、重量为w的正则字的校验子,即对于任意的f(x),存在正则字c,使得HcT=f(x)。 证明 首先有 定义一个长为n的字 c=(c1,c2,…,cn),cj=1 ⟺ ∃xi, (i-1)l+xi+1=j, 即存在xi,将其转换为数后所选择的列号恰好对应cj的位置标号j。 由于计算一个字的校验子相当于把该字非零位所对应的H矩阵的列进行相加,因此根据定义f(x)恰好就是c的校验子,即HcT=f(c)。 又由c的定义,在每一个块((i-1)l,il](i=1,2,…,w)内c有且仅有一个1,因此c是重量为w的正则字。 利用压缩函数f,定义基于编码的Hash函数 即对于给定的消息m,选择(n,k) Goppa码并按照以上定义得到一个压缩函数f,采用Augot的循环迭代方法[10]多次通过f对m的比特位进行压缩,最终得到的输出为m的Hash值。hc将任意长度的消息Hash至一个长度为r=n-k的比特串。 定理2 由上述定义得到的基于编码的Hash函数hc的输出是一个长度为n、重量为w的正则字的校验子。 证明 根据Hash函数的循环迭代构造方法,最后一轮输出的Hash值也是函数f的输出,根据定理1,对于任意的消息m,hc(m)都是一个长度为n、重量为w的正则字的校验子。 3.2 基于编码的数字签名改进算法 利用基于编码的Hash函数hc,对CFS签名算法进行改进,并将改进算法简记为CFSc签名算法,该算法的签名效率较CFS有较大提升,且其安全性并不会因此而降低。 具体的CFSc签名算法可描述如下。 (1) 参数生成 •随机选择一个F2上的(n,k) Goppa码C,纠错能力为t,校验矩阵为H,以及有效的校验子译码算法γ。 •随机选择一个F2上的n×n置换矩阵P。 •选择正整数w≤t且w|n,构造基于编码的Hash函数 •系统公开参数为〈hc,t,Hpub=HP〉,私钥为〈H,P,γ〉。 (2) 签名过程 设签名者需要签署的消息为m。 •选择随机值R,将其转换为二进制向量R,计算 s=hc(hc(m)‖R)。 •记ν=γ(s),则签名值为(R‖νP)。 (3) 验证过程 设验证者收到的消息签名对为〈m,R′‖u〉。 •计算 a=hc(hc(m)‖R′),b=HpubuT。 •若a=b则签名正确,否则签名验证失败。 CFSc签名算法中验证过程的正确性是指,若〈m,R′‖u〉是根据签名过程得到的一对合法的消息-签名对,则一定有 b=HpubuT=HP(νP)T=HPPTνT=HνT=s=hc(hc(m)‖R′)=a。 对改进后的基于编码的签名算法CFSc进行分析,并与原始的CFS算法进行对比。 4.1 算法效率分析 根据CFSc签名算法,签名者在对消息m进行签名的过程中,需要执行两次Hash运算和一次校验子译码算法。根据定理2,Hash函数hc的输出恰好是一个重量为w的正则字的校验子,不超过所选Goppa码的译码能力t。因此只要拥有校验子译码算法γ,总是可以有效译出一个长度为n、重量为w的正则字。与CFS算法平均需要尝试t!次才能得到一个可以译码的校验子相比,新的算法最大的优势在于不需要进行多次译码尝试,可以提升签名速度。从长远来看,这也使算法摆脱了参数t的限制,为提高安全性选择较大的t时不会带来签名速度的降低。 两种算法的效率对比如表1所示。 表1 算法的效率对比 4.2 算法安全性分析 与CFS签名算法相比,新算法CFSc的主要区别在于将一个随机的Hash函数h换成了基于编码的Hash函数hc,这一改动的实质是将普通Hash函数改成了陷门Hash函数,而陷门信息就是所选Goppa码译码算法中的γ。对于这一类Hash函数,知道陷门信息的人可以有效计算该Hash的逆,不知道该陷门信息的人则无法进行计算。 在CFSc中,由于译码算法中的γ是签名者所持有的私钥,除了签名者本人外没有其他任何人知道。因此只要私钥保密,该Hash函数的安全性就可以保证,CFSc的安全性就等价于CFS的安全性。因此这一改动并不会带来安全性的降低。 两种算法的安全性对比如表2所示。 表2 算法的安全性对比 作为最重要的基于编码的数字签名算法,CFS算法自提出以来其安全性和实现效率都得到了广泛的研究,但是其签名速度随参数增加而急剧降低这一缺陷却一直没有好的解决办法,因此影响了该算法的进一步应用。 将基于编码的Hash函数引入CFS签名算法,设计一种基于编码的签名改进算法CFSc。该算法在进行签名时不需要对校验子进行多次译码尝试,从而有效提升了签名速度,可以在不降低码的纠错能力t的前提下使签名时间较CFS有较大的缩短。同时该算法的安全性与CFS算法保持相同,是一种更实用的基于编码的签名算法。 [1] Overbeck R, Sendrier N. Code-based cryptography[C]//Bernstein D J, Buchmann J. Post-quantum cryptography. Berlin Heidelberg: Springer, 2009: 95-145. [2] 郑东, 赵庆兰, 张应辉. 密码学综述[J]. 西安邮电大学学报, 2013, 18(6): 1-10. [3] McEliece R J. A public-key cryptosystem based on algebraic coding theory[J]. DSN Progress Report, 1978, 42(44): 114-116. [4] Engelbert D, Overbeck R, Schmidt A. A Summary of McEliece-Type Cryptosystems and their Security[J]. Journal of Mathematical Cryptology, 2007, 1(2): 1-51. [5] Berlekamp E R, McEliece R J, van Tilborg H C A. On the inherent intractability of certain coding problems[J]. IEEE Transactions on Information Theory, 1978, 24(3): 384-386. [6] Niederreiter H. Knapsack-type cryptosystems and algebraic coding theory[J]. Problems of Control and Information Theory, 1986, 15(2): 159-166. [7] Courtois N T, Finiasz M, Sendrier N. How to achieve a McEliece-based digital signature scheme[C]//Boyd C. Advances in Cryptology-ASIACRYPT 2001. Berlin Heidelberg: Springer, 2001: 157-174. [8] Preetha M K, Sachin V, Pandu R C. On Provably Secure Code-based Signature and Signcryption Scheme[EB/OL]. (2013-07-29)[2014-11-11]. http://eprint.iacr.org/2012/585. [9] Cayrel P L, Véron P. Improved code-based identification scheme[EB/OL]. (2010-01-18)[2014-10-10]. http://arxiv.org/pdf/1001.3017v1.pdf. [10] Augot D, Finiasz M, Sendrier N. A family of fast syndrome based cryptographic hash functions[C]//Dawson E, Vaudenay S. Progress in Cryptology-Mycrypt 2005. Berlin Heidelberg: Springer, 2005: 64-83. [11] Gaborit P, Lauradoux C, Sendrier N. SYND : a fast code-based stream cipher with a security reduction[C]//IEEE International Symposium on Information Theory. France Nice: IEEE Information Theory Society, 2007: 186-190. [12] Finiasz M, Sendrier N. Security bounds for the design of code-based cryptosystems[C]//Matsui M. Advances in Cryptology-ASIACRYPT 2009. Berlin Heidelberg: Springer, 2009: 88-105. [13] Dallot L. Towards a concrete security proof of Courtois, Finiasz and Sendrier signature scheme[C]//Lucks S, Sadeghi A-R, Wolf C. Research in Cryptology. Berlin Heidelberg: Springer, 2008: 65-77. [14] Finiasz M. Parallel-CFS[C]//Biryukov A, Gong G, Stinson D R. Selected areas in cryptography. Berlin Heidelberg: Springer, 2011: 159-170. [15] Zheng Dong, Li Xiangxue, Chen Kefei. Code-based Ring Signature Scheme[J]. International Journal of Network Security, 2007, 5(2): 154-157. [16] Melchor C A, Cayrel P, Gaborit P, et al. A new efficient threshold ring signature scheme based on coding theory[J]. IEEE Transactions on Information Theory, 2011, 57(7): 4833-4842. [17] Overbeck R. A Step Towards QC Blind Signatures[EB/OL]. (2009-03-02)[2014-10-30]. http://eprint.iacr.org/2009/102. [责任编辑:瑞金] 《西安邮电大学学报》版权声明 为适应我国信息化建设的需要,扩大刊物影响,拓宽信息交流渠道,本刊已加入“中国知网CNKI系列期刊数据库”、“中国核心期刊(遴选)数据库”(万方数据——数字化期刊群)、“中国期刊网”等数据库。本刊已许可以上数据库以数字化方式复制、汇编、发行、信息网络传播本刊所载文章的全文信息。稿件一经刊登,将在本刊稿酬中一次性支付著作权使用报酬(包括印刷版、光盘版和网络版等各种使用方式的报酬)。作者向本刊提交文章的行为即视为同意我刊上述声明。 西安邮电大学学报编辑部 An improved code based digital signature algorithm REN Fang1,2, ZHENG Dong2 (1. School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;2. National Engineering Laboratory for Wireless Security, Xi’an University of Posts and Telecommunications, Xi’an 710121, China) In order to solve the problem of inefficiency of CFS algorithm, an improved code based digital signature algorithm is proposed by using code based Hash function. The output of this Hash function is a syndrome of a regular word which weight is no more than error correcting capacity of the code. The substitute of this function for the random Hash function makes the decoding algorithm execute only once in signing phase and avoid the time-consuming syndrome decoding attempt. The signing time of the improved algorithm can reduce t! times than CFS algorithm and the efficiency can get rid of the restriction from error correcting capacity. Furthermore, the securities of these two algorithms depend on the equivalent NP complete problems. digital signature, code, syndrome, Hash function, quantum attack 10.13682/j.issn.2095-6533.2015.04.008 2014-12-12 国家自然科学基金资助项目(61272037,61472472);陕西省自然科学基金重点资助项目(2013JZ020);陕西省自然科学基金资助项目(2015JQ6262);陕西省教育厅专项科研计划资助项目(2013JK1097);西安邮电大学青年基金资助项目(ZL2013-06) 任方(1981-),男,博士,讲师,从事密码学与网络安全研究。E-mail:renfang_81@163.com 郑东(1964-),男,博士,教授,博导,从事密码学与云计算安全研究。E-mail:zhengdong@xupt.edu.cn TN918.3 A 2095-6533(2015)04-0038-06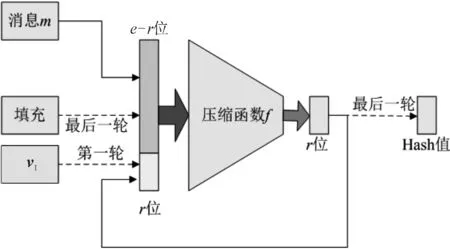
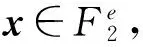
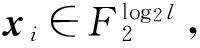
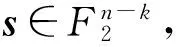
4 算法性能分析


5 结束语

