基于噪声距离的低对比度图像抗噪分割算法

田小平, 李婷婷, 吴成茂

(西安邮电大学 电子工程学院,陕西 西安 710121)

基于噪声距离的低对比度图像抗噪分割算法

田小平, 李婷婷, 吴成茂

(西安邮电大学 电子工程学院,陕西 西安 710121)

针对核空间模糊局部信息C-均值聚类算法(KWFLICM)对低对比度图像抗噪性差的不足,提出一种基于噪声距离的核空间模糊局部信息C-均值聚类算法。该算法在KWFLICM算法的基础上改变隶属度约束条件并引入噪声距离δ获得一种改进的聚类目标函数,并借鉴现有噪声聚类思想构造出具有良好抗噪性的模糊聚类迭代隶属度和聚类中心表达式,最后给出相应的聚类分割算法。实验结果表明,该改进算法对于椒盐噪声干扰的对比度较弱的灰度图像比KWFLICM聚类分割算法更有优势。

图像分割; 模糊聚类；噪声距离； 核函数

聚类分析是数据挖掘中的重要部分之一,其依据样本间关联的量度标准将其自动分成几个群组,且使同一群组内的样本相似,而属于不同群组的样本相异的一组方法[1]。图像分割是利用其灰度、颜色、纹理和形状等特征将其分成若干个特定的、具有独特性质的区域并提出感兴趣目标的技术和过程,其本质是像素聚类问题[2]。聚类方法已在图像分割中得到应用[3-7],其中模糊聚类是图像分割中最为广泛研究和应用的重要方法之一[8-9]。在模糊聚类算法中,应用最广泛的是模糊C均值(Fuzzy C-Means, FCM)算法[10],但其对噪声和孤立点比较敏感[11],并且没有考虑图像的空间邻域信息,在处理受噪声干扰的图像时常会得到不理想的分割结果[12]。针对FCM算法的缺陷,模糊局部信息C-均值(Fuzzy Local Information C-Means, FLICM)算法[13]提出一种模糊因子,将局部空间信息和局部灰度信息联系在一起；核空间模糊局部信息C-均值(Kernel Metric Local Information C-Means, KWFLICM)算法[14]将其推广至再生核空间并对其模糊权因子采用像素邻域方差信息修正,从而提高算法的鲁棒性和抗噪性,但对于对比度较弱的图像去噪效果仍较差。

针对FCM算法对噪声和孤立点比较敏感问题,噪声聚类算法[15](Noise Clustering, NC)将噪声数据看作是单独的一类,用一种参数子集来表示这一聚类,称之为噪声距离。本文将NC算法中的噪声距离和隶属度约束条件引入到KWFLICM算法中,给出一种改进的算法来改善该聚类算法的分割性能,以此提高其抗噪性。最后通过对多幅图像分割测试和比较验证该改进算法的可行性和有效性。

1 模糊聚类

1.1 模糊C-均值聚类

模糊C均值聚类算法(FCM)是从硬C均值算法发展而来的,其实质是一种基于目标函数的非线性迭代最优化方法,目标函数采用图像中各像素与每个聚类中心之间的加权欧式距离平方测度,其聚类目标函数[10]为

(1)

且满足下面约束条件[10]

(2)

其中c表示样本集的聚类数目,xi(i=1,2,…,N)是样本集,vk(k=1,2,…,c)是聚类中心,uik表示xi属于第k类区域的隶属度。d2(xi,vk)为样本xi与聚类中心vk之间的欧氏距离平方,m是模糊性加权指数,一般典型值取m=2。

隶属度uik和聚类中心vk的迭代更新表达式为

(3)

(4)

FCM算法直接用于图像存在的不足[16-17]是：(1)直接聚类分割像素非常耗时；(2)像素聚类分割未考虑邻域像素的影响,导致其抗噪性差。

1.2 核空间模糊局部信息C-均值聚类

KWFLICM算法用核距离测度代替FLICM算法中的欧式距离测度,并提出了新的局部信息加权模糊因子 ,以便提高该类算法的抗噪性能。其聚类目标表达式[14]为

(5)

模糊因子[14]

(6)

其中Ni为像素i的邻域像素集合,uik为像素xi属于第k类的隶属度；1-K(xi,vk)是邻域像素xi和聚类中心vk基于核空间的非欧氏距离测度。wij是xi周围的局部窗中的j像素的决策加权模糊因子,(1-ujk)m是一个罚值,它加速了迭代收敛到某些值的速度。约束条件同式(2)所示。

隶属度和聚类中心的迭代更新表达式为

(7)

(8)

欧氏距离和核空间距离的转换关系为

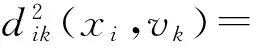
K(xi,xi)+K(vk,vk)-2K(xi,vk),

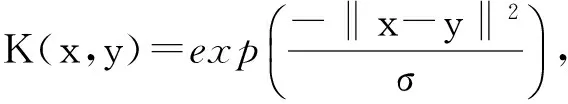
‖Φ(xi)-Φ(vk)‖2=2(1-K(xi,vk))。

2 噪声聚类

噪声聚类算法将噪声认为是独立的一类,它将噪声距离看作是常数δ即像素点距离噪声聚类中心的距离,噪声距离的表达式[13]为

(9)

在噪声聚类中像素xi的隶属度为

(10)

其中c为样本集的聚类数目,uik为样本集中像素xi属于第k类的隶属度。ui*是噪声类中的隶属度,为了达到更好的聚类效果,在噪声聚类中,隶属度约束条件设为

(11)

噪声聚类在FCM算法的基础上结合可能性聚类算法的思想改变隶属度约束条件,引入噪声距离δ,其目标函数[13]为

(12)

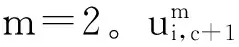
隶属度和聚类中心的迭代表达式分别为

(13)

(14)

噪声聚类算法具有鲁棒性,适合处理噪声数据集,其中噪声距离起到关键作用。可以借鉴噪声聚类的思想，将噪声距离引入到其他模糊聚类算法中，提高算法的抗噪性。

3 改进的抗噪模糊聚类算法

对KWFLICM算法的目标函数引入噪声聚类中的噪声距离,并且改变隶属度约束条件使得改进后的算法具有更广泛的抗噪性。改进后算法的目标函数为

(15)

模糊加权因子为

(16)

噪声距离为

约束条件为

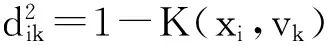
隶属度和聚类中心迭代表达式分别为

(17)

(18)

改进后的算法步骤如下。

步骤1 设置聚类数目c(2≤c≤n),模糊因子m,窗口大小Ni,噪声乘子λ,以及迭代停止条件ε。

步骤2 初始化聚类中心。

步骤3 设置循环次数计数器b=0。

步骤4 计算文献[14]中的决策加权模糊因子wij。

步骤5 利用式(9)计算噪声距离δ。

步骤6 利用式(17)更新隶属度矩阵。

步骤7 利用式(18)更新聚类中心。

4 实验结果及其分析

采用KWFLICM算法和改进算法分别对图1进行不加噪和加噪测试,对比两种算法的分割测试结果,分析改进算法的可行性和有效性。实验平台为Matlab 7.10.0,模糊因子m=2,迭代终止条件ε=0.01。聚类数目c=2。

(a) 水下目标图像

(b) 遥感卫星图像

(c) 合成图像

(d) 遥感图像

4.1 不加噪聚类分割测试

对图1分别采用KWFLICM算法和改进算法进行不加噪分割测试,测试结果分别如图2～图5所示,其中图2～图5中子图(a)为采用KWFLICM算法所得分割结果,子图(b)为采用改进算法在噪声乘子λ分别为10、1、0.05、10时所得分割结果。

(a) KWFLICM算法

(b)改进算法

(a) KWFLICM算法

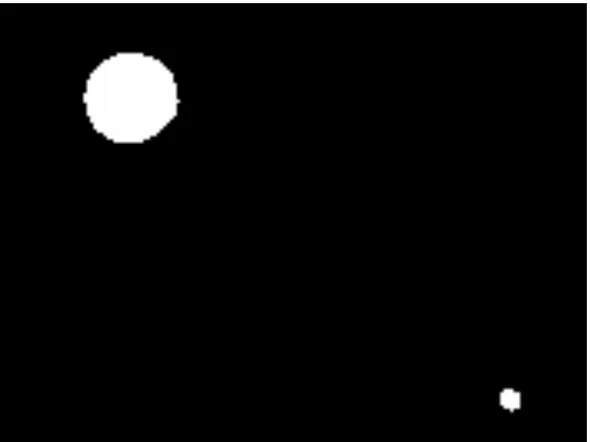
(b)改进算法

(a) KWFLICM算法

(b) 改进算法

(a) KWFLICM算法

(b) 改进算法

从图2、图3和图5所示分割结果来看,在不受噪声干扰的情况下, KWFLICM算法有良好的分割性能,能够将测试图像中的目标清晰的分割出来,而改进算法同样可以通过调节噪声乘子λ来取得良好的分割效果,两种算法分割性能相当。而从图4可以看出采用改进算法所得分割结果相对优于KWFLICM算法,图4(a)相对于图4(b)所标记的相应区域,其分割效果较差。其中图4(a)中正方形、椭圆所标记的区域没有将图1(c)中的局部细节分割出来,相对于图4(b)所对应标记区域的分割效果,其分割效果较差,圆形、长方形所标记的区域分割连续程度较差,而图4(b)所对应的标记区域分割连续程度较好。

由以上分割结果可知,在不受噪声干扰的情况下,改进算法可以准确的将测试图像中的目标清晰的分割出来,是可行且有效的。

4.2 随机椒盐噪声干扰聚类分割测试

为了进一步验证改进算法的分割性能,对图1添加椒盐噪声,并对其噪声干扰图像分别采用KWFLICM算法和改进算法进行聚类分割测试,图6～图9中的子图(a)为噪声干扰图,子图(b)为对应的直方图,子图(c)为采用KWFLICM算法所得分割结果,子图(d)为采用改进算法所得分割结果。通过所得结果来验证改进算法的抗噪性。

4.2.1 水下目标图像聚类分割测试

在图1(a)添加概率为0.1的椒盐噪声,采用KWFLICM算法和改进算法(λ=0.1)对所得噪声干扰图进行分割测试所得结果如图6所示。

(a) 噪声干扰图

(b) 直方图

(c) KWFLICM算法

(d) 改进算法

从图6所示分割结果来看,采用KWFLICM算法不能有效地将图1(a)所示水下目标图像的目标轮廓分割出来,而采用改进算法可以明显的将其目标轮廓分割出来,分割效果较好。

4.2.2 遥感卫星图像聚类分割测试

在图1(b)添加概率为0.2的椒盐噪声,采用KWFLICM算法和改进算法(λ=0.03)对所得噪声干扰图进行分割测试所得结果如图7所示。

(a) 噪声干扰图

(b) 直方图

(c) KWFLICM算法

(d) 改进算法

从图7所示分割结果来看,采用KWFLICM算法不能有效地将图1(b)所示遥感卫星图像的弱目标分割出来,而采用改进算法可以将其弱目标明显的显现出来,分割效果较好。

4.2.3 合成图像聚类分割测试

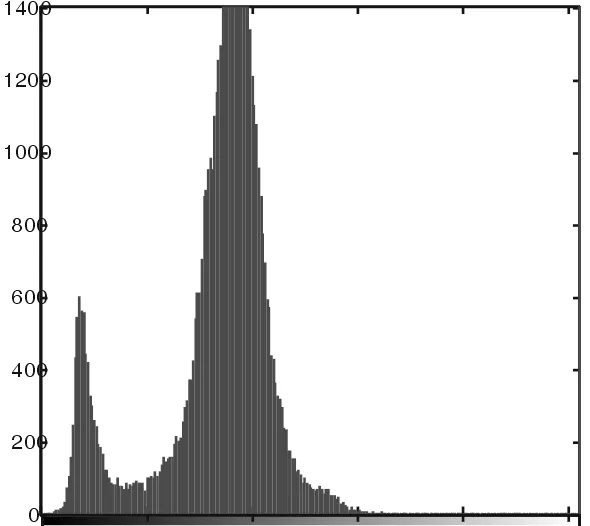
在图1(c)添加概率为0.05的椒盐噪声,采用KWFLICM算法和改进算法(λ=0.01)对所得噪声干扰图进行分割测试所得结果如图8所示。

(a) 噪声干扰图

(b) 直方图

(c) KWFLICM算法

(d) 改进算法

从图8所示分割结果来看,采用KWFLICM算法不能将图1(c)所示合成图像目标的主要轮廓分割出来,而采用本文改进算法可以将其目标的主要轮廓清晰的显现出来,分割效果很好。

4.2.4 遥感图像聚类分割测试

在图1(d)添加概率为0.3的椒盐噪声,采用KWFLICM算法和改进算法(λ=1)对所得噪声干扰图进行分割测试所得结果如图9所示。

从图9所示分割结果来看,采用KWFLICM算法不能将图1(d)所示遥感图像目标的大致轮廓分割出来,而采用本文改进算法虽然没有将图1(d)的目标清晰的分割出来,但相对于KWFLICM算法本文改进算法可以将图1(d)的局部目标轮廓大致显现出来,相对分割效果较好。

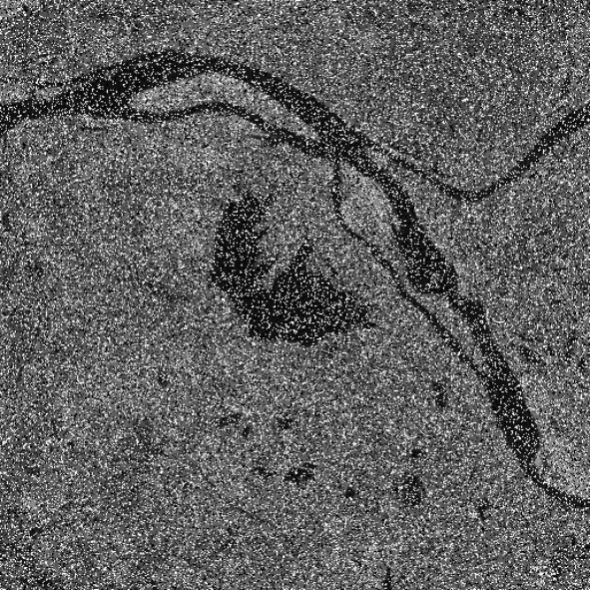
(a) 噪声干扰图

(b) 直方图

(c) KWFLICM算法

(d) 本文改进算法

综合以上实验对比分析可知,对于灰度分布范围较窄的低对比度灰度图像,改进算法相比KWFLICM算法在抗椒盐噪声干扰方面更有优势。

5 结束语

结合噪声距离和KWFLICM算法,通过改变KWFLICM算法的隶属度约束条件提出一种改进算法。分别采用KWFLICM算法和改进算法对不受噪声干扰的图像和受椒盐噪声干扰的图像聚类分割,对比分析所得的聚类分割结果,实验结果表明改进算法可以准确的将测试图像中的目标清晰的分割出来,相比KWFLICM算法更有利于椒盐噪声干扰的灰度分布范围较窄的低对比度灰度图像分割需要。

[1] Kantardzic M.数据挖掘—概念、模型、方法和算法[M].闪四清,陈茵,程雁,等译.北京:清华大学出版社, 2003:101.

[2] 章毓晋.图像分割[M].北京:科学出版社,2001:2-3.

[3] 林开颜,徐立鸿,吴军辉.快速模糊C均值聚类彩色图像分割方法[J].中国图象图形学报:A辑,2004,9(2): 159-163.

[4] Zhao Feng,Jiao Licheng,Liu Hanqiang.Fuzzy c-means clustering with non local spatial information for noisy image segmentation[J].Frontiers of Computer Science in China,2011,5(1):45-56.

[5] 余锦华,汪源源,施心陵.基于空间邻域信息的二维模糊聚类图像分割[J].光电工程,2007,34(4): 114-119.

[6] Chen Long, Chen C L P, Lu Mingzhu. A multiple-kernel fuzzy c-means algorithm for image segmentation[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2011, 41(5): 1263-1274.

[7] 赵凤,范九伦,支晓斌,等.基于灰度和空间特性的谱聚类图像分割[J]. 西安邮电学院学报, 2012, 17(1):52-57.

[8] Naz S, Majeed H, Irshad H. Image segmentation using fuzzy clustering: A survey[C]// the 6th International Conference on Emerging Technologies, Piscataway, NS, USA:IEEE, 2010: 181-186.

[9] 李琳.范九伦.赵凤.模糊C-均值聚类图像分割算法的一种改进[J]. 西安邮电大学学报,2014, 19(5):56-60.

[10] Bezdek J C, Hathaway R J. Convergence and theory for fuzzy C-means clustering: counterexamples and repairs [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987,17(5): 873-877.

[11] Krishnapuram R, Keller J M. The possibilistic c-means algorithm: insights and recommendations[J]. IEEE Transactions on Fuzzy Systems ,1996, 4(3): 385-393.

[12] Chuang K S,Tzeng H L, Chen S, et al. Fuzzy C-Means Clustering with Spatial Information for Image Segmentation[J].Computerized Medical Imaging and Graphics, 2006,30(1): 9-15.

[13] Krinidis S, Chatzis V. A robust fuzzy local information C-means clustering algorithm [J]. IEEE Transactions on Image Processing,2010,19(5): 1328-1337.

[14] Gong Maoguo, Liang Yan, Shi Jiao, et al. Fuzzy C-Means Clustering With Local Information and Kernel Metric for Image Segmentation[J]. IEEE Transactions on Image Processing, 2013, 22(2): 573-584.

[15] Dave R N, Robust fuzzy clustering algorithms[C]//Second IEEE International Conference on Fuzzy Systems, San Francisco, CA :IEEE,1993: 1281-1286.

[16] 丁震,胡钟山,杨静宇,等.一种基于模糊聚类的图像分割方法[J].计算机研究与发展,1997,34(7):536-541.

[17] Pham D L. Fuzzy Clustering with Spatial Constraints[C]//International Conference on Image Processing, Piscataway, NS: IEEE, 2002: 65-68.

[责任编辑：祝剑]

A noise-robust segmentation algorithm of low contrast imagebased on noise distance

TIAN Xiaoping, LI Tingting, WU Chengmao

(School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121,China)

A fuzzy C-means clustering algorithm with local information based on the noise distance algorithm is proposed in this paper to tackle at the problem that the fuzzy C-Means clustering with local information and Kernel metric (KWFLICM) algorithm has poor noise-robust for low contrast image. On the basis of the existing KWFLICM algorithm, this algorithm changes constraints on membership and introduces noise distanceδto get an improved noise-robust clustering objective function. Based on existing noise clustering idea, this algorithm constructs fuzzy clustering iterative expressions of membership and cluster centers with good noise resistance. Then it gives the corresponding clustering segmentation algorithm. Experimental results show that the improved algorithm for low-contrast image by salt and pepper noise interference is more superiority than that of the existing KWFLICM clustering segmentation algorithm.

image segmentation ,fuzzy clustering,noise distance,kernel functions

10.13682/j.issn.2095-6533.2015.04.007

2015-01-04

国家自然科学基金重点资助项目(61136002);陕西省自然科学基金资助项目(2014JM8331, 2014JQ5138,2014JM8307)

田小平 (1963-),男,教授,从事信号与信息处理技术研究。E-mail:xptian@xupt.edu.cn 李婷婷 (1991-),女,硕士研究生,研究方向为图像处理及其信息安全。E-mail: litingting3266@163.com

TP391.4

A

2095-6533(2015)04-0032-06