基于遗传算法的火炮反后坐装置结构多目标优化研究

周乐，杨国来，葛建立，王飞

(南京理工大学 机械工程学院，江苏 南京210094)

0 引言

反后坐装置是火炮的重要组成部分，很大程度上影响了火炮的射速和精度。对于火炮反后坐装置的动力学分析和优化，国内外许多研究者进行了大量的研究，More［1］通过建立某牵引火炮多体动力学模型来对其动态响应进行研究。Dias 等［2］利用多体模型和遗传算法获得了复杂车体的防撞结构和能量吸收装置的最佳特性。周成等［3］通过建立节制杆优化模型对后坐阻力和后坐长度进行了优化。宗士增等［4］建立了反后坐装置动力学耦合模型进行了数值仿真并以节制杆尺寸为设计变量对其进行优化。蔡文勇等［5］将遗传算法和多体动力学联合以炮口扰动为优化目标进行了火炮动力学优化。梁传建等［6］建立了非线性有限元模型并通过数值计算研究了制退机不同布置位置对炮口扰动的影响规律。

总结这些文献，对反后坐装置的优化工作局限于制退机结构，还未考虑到总体结构对其影响。本文以某型火炮样机为研究对象，建立其刚柔耦合多体动力学模型，选取制退机节制杆沟槽和部分总体结构参数为设计变量，不仅考虑最大后坐阻力和后坐位移的优化，同时以弹丸出炮口瞬间的炮口扰动为优化目标，基于小生境遗传算法对反后坐装置进行多目标动力学优化设计研究，寻求各设计参数间更优的匹配关系。

1 遗传算法与动力学优化

多目标优化问题的解实际上是一个最优解集合，即Pareto 最优解。遗传算法通过选择、交叉、变异3 个操作来产生最优解。基于适应度共享小生境的遗传算法可以定义共享函数来调整个体适应度，该算法可以更好地保持解的多样性，其全局寻优能力和收敛速度使其更适合于复杂函数的多目标优化问题［7-9］。

在ADAMS View 环境下进行火炮结构参数优化不仅难以实现部分设计变量的定义，其简单优化方法也不适合火炮的复杂结构。因此通过对该软件底层计算模块的二次开发，编写遗传算法FORTRAN语言优化模块，将遗传优化算法与求解器模块联合，可以完成对设计变量的必要修改，实现对模型的完全控制，以达到最优解的效果。联合仿真优化的流程图如图1 所示。

2 反后坐装置优化

2.1 火炮动力学模型

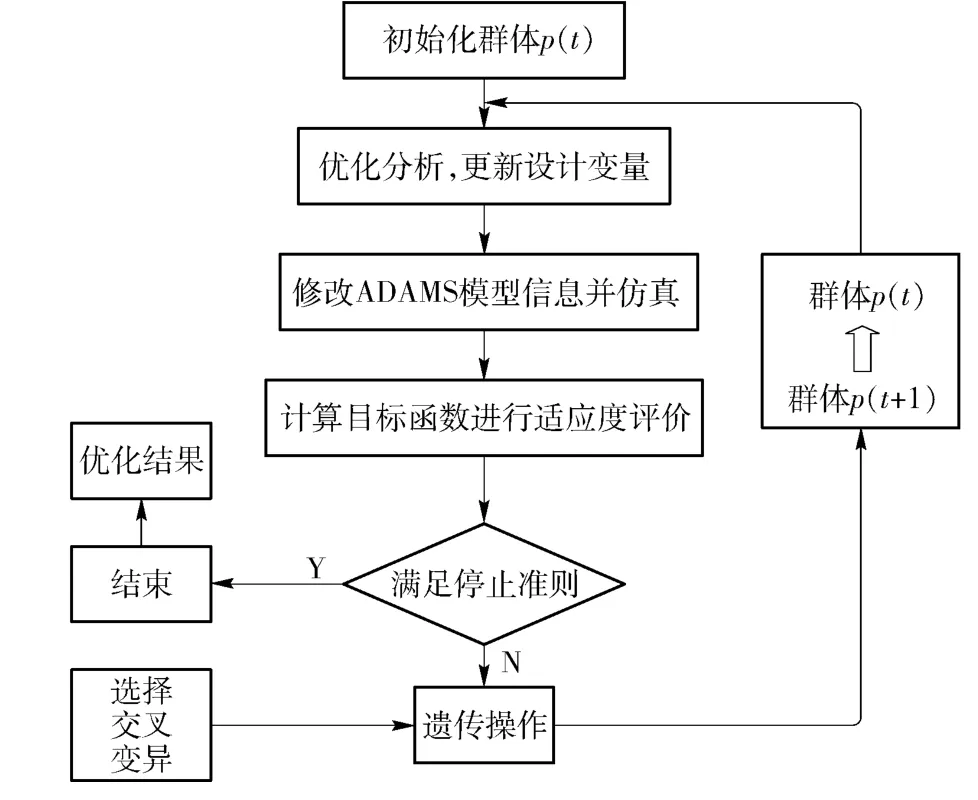
图1 优化流程框图Fig.1 Flow chart of optimization

火炮发射过程其受力和运动现象十分复杂。建模时应考虑其主要运动和受力情况，使其尽量符合实际。本文考虑身管、摇架、上架为柔性体，其他部件如炮口制退器、炮尾、下架等为刚体。整个模型由IDEAS 建立的精确的实体模型以及基于Hypermesh生成的柔性体.mnf 文件导入ADAMS 来得到。火炮发射过程中载荷主要有炮膛合力、制退机力、复进机力、平衡机力。这部分发射载荷可通过FORTRAN语言编写程序，生成动态链接库. dll 文件再嵌入动力学模型来实现。驻锄与土壤、底盘与地面、高低机齿弧间作用力采用非线性弹簧和阻尼来模拟。

全炮拓扑结构示意图如图2 所示。

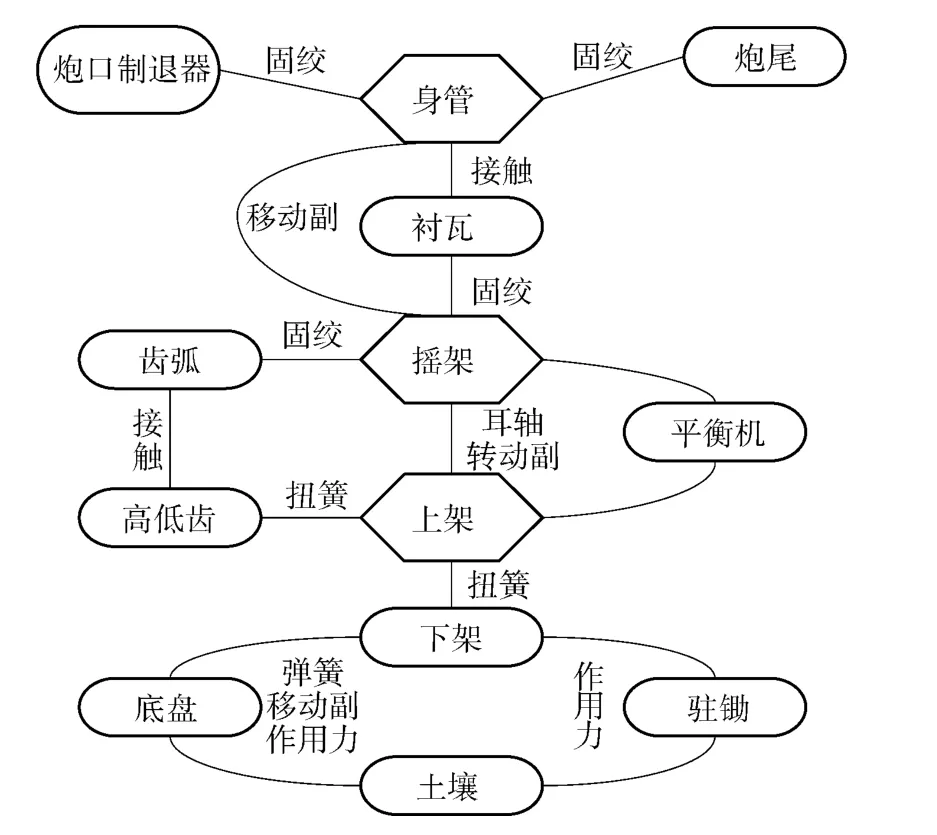
图2 全炮结构示意图Fig.2 Schematic Diagram of gun structure

2.2 火炮反后坐装置优化

2.2.1 优化模型

本文对射角为0°的火炮模型进行优化，建立的优化模型如下:

1)设计变量

一般对制退机节制杆尺寸进行优化，选取节制杆沟槽深度为设计变量;此外，从总体设计角度出发，以后坐部分质量、后坐部分质心位置、炮口制退器质量、前衬瓦与耳轴中心在同一轴线方向上距离、前后衬瓦之间距离、制退机左右布置参数、高低机扭簧刚度系数、方向机扭簧刚度系数等部分总体参数为设计变量，对火炮进行多目标优化。

2)目标函数

对后坐阻力F、后坐位移s 及出炮口瞬间的炮口垂直线速度v、炮口高低角速度ω﹑炮口高低角θ进行归一化处理，分别给各目标子函数按重要性赋予相应的权系数，总目标函数φ 可表示为各个子目标函数的线性加权，适应度函数f 取总目标函数的倒数:

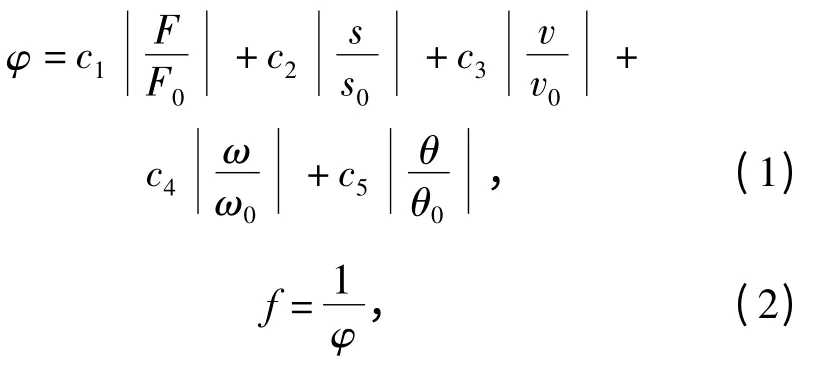
式中:F0、s0、v0、ω0、θ0为初始值;c1～c5为加权系数，分别取值为0.25、0.25、0.05、0.15、0.30，其值之和为1.

2.2.2 优化结果及分析

本文利用小生镜遗传算法和ADAMS SOLVER求解器联合优化的方法进行了火炮系统动力学优化计算，该算法一次可以搜索出多组优化方案，选取其中一组优化结果进行分析。后坐阻力、位移及炮口扰动优化前后随时间变化的比较曲线如图3 ～图7所示。

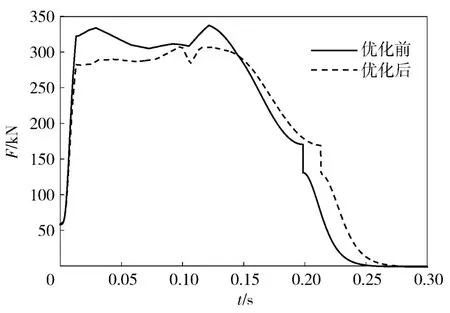
图3 后坐阻力曲线对比Fig.3 Comparison of recoil resistances

对比图3 ～图7 优化前后曲线及表1 可知，优化后后坐过程中后坐阻力峰值Fmax和后坐最大位移smax小于优化前，出炮口瞬间高低角θ0变小，角速度ω0和线速度v0幅值变小，曲线变化趋势更加平缓。说明建立的优化模型可以实现其优化目的。

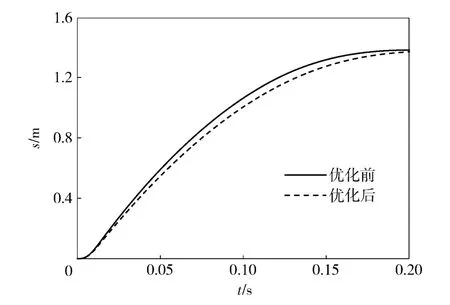
图4 后坐位移曲线对比Fig.4 The comparison of displacement

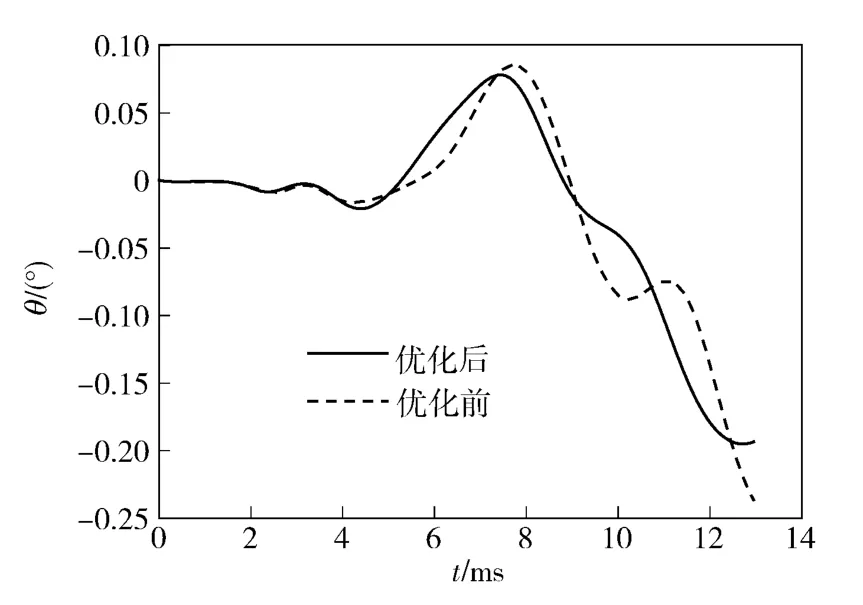
图5 优化前后高低角曲线Fig.5 Curves of elevation angle before and after optimizing

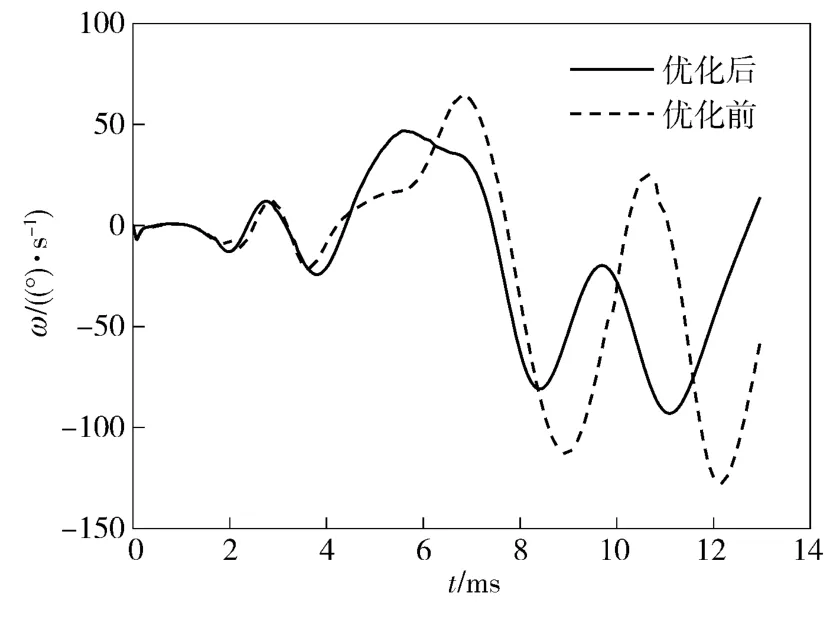
图6 优化前后角速度曲线Fig.6 Curves of angular velocity before and after optimizing

3 结论

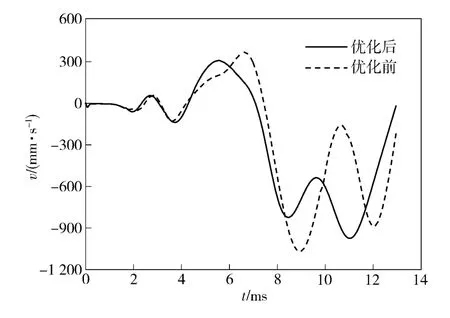
图7 优化前后高低线速度曲线Fig.7 The curves of velocity before and after optimizing

表1 优化前后结果对比Tab.1 The comparison of results before and after optimizing

对比初始与优化后的后坐阻力和炮口扰动值，后坐阻力和炮口扰动有了明显降低，这表明通过反后坐装置结构和总体结构的优化，最大后坐阻力、后坐位移、炮口扰动等得到了较好的控制，充分说明了火炮系统总体方案优化的重要性和必要性。而通过遗传算法和动力学优化结合的方法可提供多组优化结果，选择更具有灵活性。

References)

［1］More A K. Multi-body dynamics and design optimization for a towed gun［D］. Nanjing:Nanjing University of Science and Technology，2008.

［2］Dias J P，Pereira M S. Optimization methods for crashworthiness design using multibody models［J］. Computers and Structures，2004，82(17/18/19):1371 -1380.

［3］周成，顾克秋，邵跃林.火炮制退机节制杆优化设计［J］. 火炮发射与控制学报，2012，12(4):68 -70.ZHOU Cheng，GU Ke-qiu，SHAO Yue-lin.Optimal design of hrottling bar in gun recoil mechanism［J］. Journal of Gun Launch ＆Control，2012，12(4):68 -70.(in Chinese)

［4］宗士增，钱林方，徐亚栋.火炮反后坐装置动力学耦合分析与优化［J］.兵工学报，2007，28(3):272 -275.ZONG Shi-zeng，QIAN Lin-fang，XU Ya-dong. Dynamic coupling analysis and optimization of gun recoil mechamism［J］.Acta Amamentarii，2007，28(3):272 -275.(in Chinesse)

［5］蔡文勇，马福球，杨国来.基于遗传算法的火炮总体参数动力学优化［J］.兵工学报，2006，27(6):974 -977.CAI Wen-yong，MA Fu-qiu，YANG Guo-lai. Dynamic overall parameter optimization of howitzer with genetic algorithm［J］. Acta Armamentarii，2006，27 (6):974 -977.(in Chinese)

［6］梁传建，杨国来，葛建立，等.反后坐装置结构布置对炮口振动影响的研究［J］. 兵工学报，2013，34(10):1209 -1214.LIANG Chuan-jian，YANG Guo-lai，GE Jian-li，et al.Study on influence of structural arrangement of recoil mechanism on muzzle vibration of gun［J］. Acta Armamentarii，2013，34(10):1209 -1214.(in Chinese)

［7］Goldberg D E，Richardson J. Genetic algorithms with sharing for multimodal function optimization［C］∥Proceedings of the Second Int Conference on Genetic Algorithms and Their Applications. NJ:Lawrence Erlbaum Associates Inc，1987:41 -49 .

［8］Xu Z，Lu S S.Multi-objective optimization of sensor array using genetic algorithm［J］. Sensors and Actuators，2011，160(1):278 -286.

［9］Ericksona M，Mayer A，Hornb J. Multi-objective optimal design of groundwater remediation systems:application of the niched Pareto genetic algorithm (NPGA)［J］. Advances in Water Resources，2002，25(1):51 -65.