基于混沌三次指数平滑模型的CPI预测研究

杨文光， 严　哲， 于　健

(华北科技学院 基础部， 河北 三河　065201)



基于混沌三次指数平滑模型的CPI预测研究

杨文光， 严哲， 于健

(华北科技学院 基础部， 河北 三河065201)

摘要：提出了一种新的混沌三次指数平滑算法，该算法加入了遗传算法的变异算子，可以实现混沌优化选择三次指数平滑模型中的平滑系数.同时，引入了遗传算法的种群概念，提高了算法的并行性运算能力.通过CPI序列数据预测研究，进行了算法的有效性验证.试验结果表明混沌三次指数平滑模型可以通过多次混沌迭代搜索，得到全局最优的平滑系数，提高了最终预测精度.

关键词：混沌优化； 三次指数平滑模型； 变异算子； CPI

0引言

居民消费价格指数(Consumer Price Index,CPI)是一个反映居民家庭一般所购买的消费商品和服务价格水平变动情况的宏观经济指标.它是消

费商品及服务项目的价格水平随时间而变动的相对数，是直观反映居民家庭购买消费商品及服务的价格水平的变动情况.研究和预测CPI对于监测和指导经济分析、决策具有非常重要的参考价值.不同的文献分别使用小波分解自回归模型[1]、GM(1,1)模型[2]、灰色加权马尔科夫模型[3]、混沌神经网络模型[4]、贝叶斯时间序列预测模型[5]、T-S模糊神经网络组合模型[6]等.指数平滑法(ES)是由美国学者布朗(Robert G.Brown)首先提出，它是在移动平均法的基础上发展出的一种时间序列分析法，在经济、管理等预测方面获得了广泛成功应用[7].例如，用于中短期经济发展趋势预测，库存预测，以及生产预测等.

指数平滑模型分为一次指数平滑、二次指数平滑和三次指数平滑.当数据无明显趋势变化时，可使用一次指数平滑模型.二次指数平滑模型是对一次指数平滑的再平滑，它适合具有线性趋势的时间序列.三次指数平滑模型是在二次指数平滑模型的基础上再平滑，几乎可以适用于所有时间序列数据预测问题.指数平滑法兼具了全期平均和移动平均所长，既不舍弃过去的数据，又能够随着数据的远离，逐渐减少过去的影响力.其基本原理是，任一期的指数平滑值是本期实际观察值与前一期指数平滑值的加权平均[8].本文对于CPI预测引入三次指数平滑模型，以期进一步提高预测精度.

在指数平滑模型中，平滑系数的选择是各期影响程度的重要体现，它取值的大小直接关系到各期数据预测的精确度[9].目前，平滑系数的选择还存在很大的困难，有关平滑系数的确定涌现出了很多方法，比如，试算法、经验判断法、差分-比率-均值法等[9,10].但是这些方法对平滑系数的选择存在很大的局限性，或者具有很大的随意性、片面性与不确定性，或者计算非常的繁琐.

本文将引用混沌优化算法作用于平滑系数的选择上，建立基于混沌优化算法的三次指数平滑模型.在具体实施过程中，为了保证搜索到全局最优的平滑系数，将结合遗传算法的种群与变异算子改进传统的混沌优化算法，提高计算的并行性，加快搜索速度.最后结合中国CPI序列数据，建立了改进的混沌三次指数平滑CPI模型，通过与VAR模型、T-S模糊神经网络组合模型预测结果进行比较，突出了本文所构建模型的有效性和可行性.

1指数平滑法

指数平滑法来源于移动平均法，且融合了时间序列各时期权数的加权平均内容，根据使用对象和环境不同的需要，可以分别采用一次指数平滑法、二次指数平滑法与三次指数平滑法，甚至是更高次的指数平滑法.下面对三次指数平滑法做一简单介绍.

三次指数平滑预测是对二次指数平滑的再平滑.它设计的基本思想是，预测值是以前观测值的加权求和，且对不同的数据给予不同的权重，新数据给予较大的权重，旧数据给予较小的权重.

1.1　一次指数平滑法公式

(1)

1.2　二次指数平滑法公式

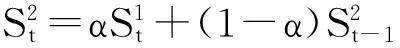
Yt+T=at+bt·T

(2)

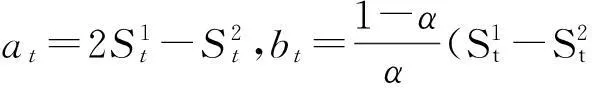
1.3　三次指数平滑法公式

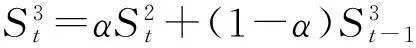
Yt+T=at+bt·T+ct·T2

(3)

其中,

bt=

在指数平滑模型中，平滑系数选择是相当重要的,它体现了各期的影响程度，关系到对各期数据预测的影响[3].平滑系数的确定现在涌现出了很多方法，比如，试算法、经验判断法、差分-比率-均值法等[3,4].但是这些方法对平滑系数的选择存在很大的局限性，本文引用混沌体系作用于平滑系数的选择上.

2基于三次指数平滑模型的混沌优化算法

混沌现象是指发生在确定性系统中显现出类随机性、遍历性、不确定性、不可预测性的不规则运动.但是混沌并不是一片混乱，而是非线性动力学的一种特有的运动形式，在无序中蕴含着有序.基于混沌现象的遍历性特点设计的混沌优化算法是一种全局性优化算法，体现了混沌现象丰富的时空状态[11].为了寻找体现全局最优的平滑系数α，避开主观性影响，下面对于α的寻优将采用混沌的遍历性.

2.1　基于三次指数平滑模型改进下的混沌优化算法

一维Logistic映射从数学形式上来看是一个非常简单的混沌映射，但却具有非常复杂的动力学行为，其表达式为：

xn=μxn-1(1-xn-1)

(4)

式中,μ∈[0,4]，xn∈[0,1]，n=0,1,2,…，此时系统处于混沌状态.当μ=4时，Logistic处于完全混沌状态，经过N次迭代(N足够的大)，系统便能够遍历区间中的所有值[12].在给定初值x0=0.01,μ=3.8情况下的运行状态如图1所示，表现出非常明显的混沌性、非周期性与非收敛性.

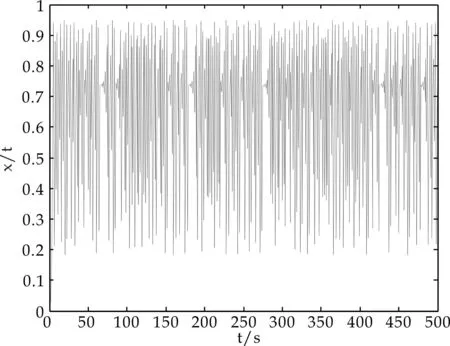
图1　Logistic混沌状态

基于三次指数平滑模型的混沌优化算法将在原始混沌优化算法基础上引入改进平滑系数α，通过与遗传算法种群、变异算子等概念的融化，达到提高算法性能的目的[13,14]，算法的基本实现步骤设计如下：

Step 1随机产生一初始种群，设种群个体数为n个，状态值x∈[a,b]，选择Logistic映射xn=μxn-1(1-xn-1)，将其带入目标函数f(x)=x×(b-a)+a；

Step 2通过随机的方式产生种群的初始值xi0∈[0,1](i=1,…,n)，计算函数zi0=f(xi0)；然后将zi0带入函数F(z).而F(z)为三次指数平滑模型均方误差值函数，z为平滑系数；

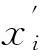
Step 4进行m次迭代，产生最终的最优解F*和个体z*；

Step 5进行二次载波，缩短搜索范围，加强局部搜索，产生新的边界a=a1,b=b1；

Step 6类似于第一次载波，生成种群，进行若干次迭代，产生最优个体z*，即平滑系数.将其带入三次指数平滑模型，得出预测结果.

2.2　算法说明

在算法实现过程中引入遗传算法的种群概念目的在于使得算法具有并行性.混沌优化算法可以保证算法具有全局搜索能力，使算法保持了良好的性能.在Step3中加入了遗传算法的变异算子，其变异算子公式为：

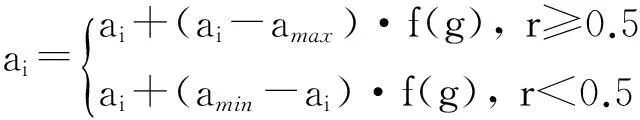
其中，ai是第i个个体，以变异概率Pc对其进行变异，amax为ai上界，amin为下界；f(g)=r2(1-g/Gmax)2，r2是一个随机数，g是当前迭代次数，Gmax是最大迭代数.

在Step5中，进行第二次载波，目的在于改变搜索尺度，进行小范围搜索，从次优解找到最优解.进而选出最适平滑系数，建立最终的三次指数平滑模型.

3实例分析

利用上面所构建算法对中国CPI序列数据建立三次平滑模型，从中国统计年鉴上选取以2000年1月到2013年2月的CPI数据作为训练数据，建立适当模型，另外选择2013年3月到5月的CPI数据作为测试数据，以便对模型进行测试检验.在下面的算法实施过程中的一些重要参数选择如下：算法混沌迭代次数为500次，变异概率Pc=0.001，种群个数为n=20.

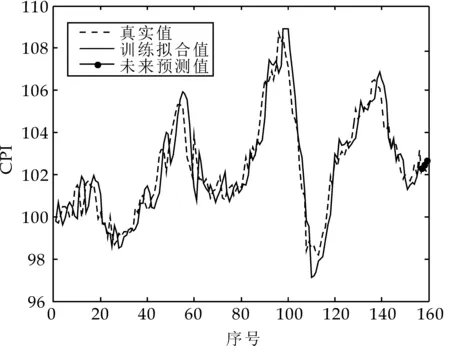
图2　混沌三次指数平滑模型预测

图3　CPI预测均方误差迭代变化值

为了更好地研究所构建模型的特点，本文选择向量自回归(VAR)模型[15]、T-S模糊神经网络组合模型预测结果[6]对于同一组CPI数据进行了预测比较，比较结果如表1所示.其中，方法1指代VAR模型，数据显示相对误差最大，方法2指代T-S模糊神经网络组合模型，相对误差居中，表1数据显示本文方法的相对误差最小.

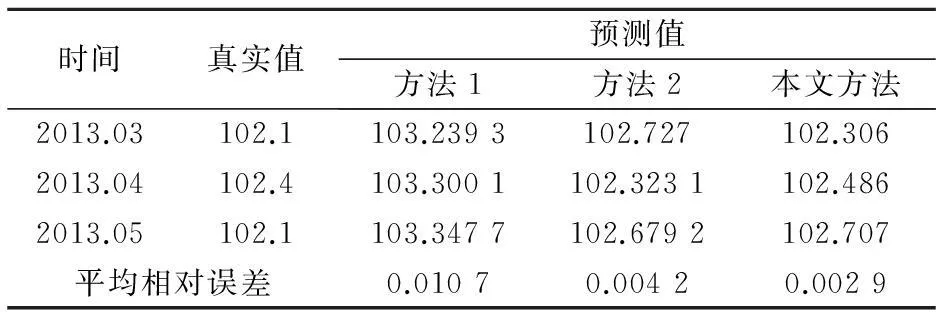
表1　三种预测模型比较结果

由上述实验证明，本文所建立模型相对于前两种模型，预测精度有了一定程度的提高，在短期预测方面具有可行性，是一种有效可行的方法.

4结论

基于三次指数平滑模型的混沌优化算法充分利用了时间序列的全部数据的内在规律，三次指数平滑模型在处理过程中将数据进行加权，简洁方便，同时避免了人为指定平滑系数的局限，实现三次指数平滑模型性能的改善.

混沌优化算法有自己的特性，它可以遍历整个给定的空间，但混沌具有固有的不均匀性，本文在具体的处理过程中引入了遗传算法的种群概念和变异算子操作，较好地克服了这种不均匀性，并且加强了算法的并行性.

总之，用混沌优化算法选择平滑系数，建立三次指数平滑模型，结合具有非线性、时变特点的CPI数据进行了算法的有效性验证.结果表明本文所建立的模型具有可行性，短期预测性能优化相关文献，具有较好的推广应用价值.

参考文献

[1] 陈升，李星野.基于小波分解自回归模型的CPI预测[J].统计与决策，2012,28(1):18-20.

[2] 王晓东，史丽敏.基于最小一乘准则GM(1,1)模型的CPI预测[J].统计与决策，2015,31(3):81-83.

[3] 田红霞.基于两次改进灰色加权马尔科夫模型的CPI预测[J].中北大学学报(自然科学版)，2015,36(2):113-117.

[4] 王维，范彦伟.基于混沌神经网络算法的CPI预测[J].统计与决策，2012,28(10)：22-24.

[5] 陈镇坤，刘金山.基于MCMC的贝叶斯时间序列CPI预测模型[J].统计与决策，2015,31(3):65-67.

[6] 荀新新，张德生.基于T-S模糊神经网络组合模型的CPI预测[J].陕西科技大学学报(自然科学版)，2014,32(3):173-176.

[7] 安鸿志.时间序列分析与应用[M].北京：科学出版社，1983.

[8] 侯琼煌，杨航.基于三次指数平滑模型的雾霭天气分析与预测[J].环境保护科学，2014,40(6):73-77.

[9] 王长江.指数平滑法中平滑系数的选择研究[J].中北大学学报(自然科学版),2006,27(6):558-561.

[10] 张雪琴.关于“指数平滑法”的研究[J].内蒙古农业大学学报，2006,27(4):153-156.

[11] 王凌，郑大钟.混沌优化方法的研究进展[J].计算技术与自动化，2001,20(1):1-5.

[12] 梁瑞鑫，郑德玲.基于区间套混沌搜索的混合优化方法[J].北京科技大学学报，2002,24(3):342-344.

[13] 费春国，韩正之.一种改进的混沌优化算法[J].控制理论与应用,2006,23(3):471-474.

[14] 李亚东，李少远.一种新的遗传混沌优化组合方法[J].控制理论与应用,2002,19(1):143-145.

[15] 倪延延，张晋昕.向量自回归模型拟合与预测效果评价[J].中国卫生统计,2014,31(1):53-56.

CPI forecasting based on chaotic cubic

exponential smoothing model

YANG Wen-guang, YAN Zhe, YU Jian

(Department of Basic Course, North China Institute of Science and Technology, Sanhe 065201, China)

Abstract:A new chaotic cubic exponential smoothing algorithm is proposed in this paper, which joined the mutation operator of genetic algorithm, and can be used to select the smoothing coefficient of cubic exponential smoothing model.At the same time, the concept of population genetic algorithm is introduced to improve the parallel computing ability of the algorithm.The validity of the algorithm is verified by CPI sequence data prediction.The experiment results show that the global optimal smoothing coefficient can be got by the chaotic cubic exponential smoothing model with many times of iteration,and the final prediction accuracy is improved.

Key words:chaotic optimization; cubic exponential; mutation operator; CPI

作者简介:杨文光(1981-)，男，河北涞水人，讲师，硕士，研究方向：模糊系统与神经网络

基金项目：中央高校基本科研业务费资助项目(3142015040, 3142014127); 华北科技学院高等教育科学研究资助项目(HKJYZD201213,HKJYZD201336); 华北科技学院重点学科项目(HKXJZD201402)

*收稿日期:2015-09-17

中图分类号：C81

文献标志码：A

*文章编号：1000-5811(2015)06-0179-04