SNOMED编码校验位算法解析及其对中医术语编码的意义

成福春，张平，刘华，房敏

1.上海中医药大学附属岳阳中西医结合医院，上海 200437；2.上海中医药大学附属曙光医院，上海 201203

SNOMED编码校验位算法解析及其对中医术语编码的意义

成福春1，张平2*，刘华1，房敏1

1.上海中医药大学附属岳阳中西医结合医院，上海 200437；2.上海中医药大学附属曙光医院，上海 201203

本文讨论了编码之中常用到的按位累加取模、多项式乘法累加取模等校验位算法的优缺点，尤其是对系统化医学术语集（SNOMED）编码采用二面体群D5校验位算法作了较深入的讨论。二面体群D5算法不仅可以校验出所有一位错误及相邻位置换位错误，而且不需要增加字母 X，是一种非常理想的校验位算法。国内目前尚无一套既具有信息技术特征，又具有中医学科本身特征的编码化的术语集，SNOMED编码采用二面体群D5校验位算法，对于中医术语编码具有重要的借鉴意义。

中医术语；术语编码；系统化医学术语集；校验位算法；二面体群D5

医学术语及其编码化，对于规范临床数据采集，数据检索分析利用、提升医疗质量以及研究的深度，具有重要意义[1]。系统化医学术语集-临床术语（ systematized nomenclature of medicineclinical terms, SNOMED CT）通过编码进行世界范围内的统一术语交流，即代码唯一，或称概念唯一。但是代码所代表的内容其形式可以多样，如英文形式、中文形式或者各国语言形式。通过定义代码与代码之间的关系，来体现学科本身的逻辑与语义。

1 系统化医学术语集-临床术语编码简介

在SNOMED CT术语体系中，赋予每一个特定术语一个代码，即扩展版的SNOMED CT概念标识符（SCTID字段）。代码本身不要求有特别的含义，只是代表这个术语本身，利于计算机处理。

在代码结构中，具有相关的属性信息，如extension item identifier（扩展项目标识符），共8位，代表具体的项目编码；namespace identifier（名称空间标识符），共7位，代表维护代码的机构；partition identifier（部分标识符），2位，10代替概念，20代表描述，30代表关系；最后一位是check-digit（校验位），便于计算机自动纠错。SNOMED通过3张表来体现，即概念表、定义表、关系表。SCTID是概念表中的最重要的字段。目前扩展版的SCTID字段结构如图1。

图1 扩展版的SCTlD数字编码结构

虽然用户可能很少手工录入SCTID，但是还是有可能会发生这种情况。在手工录入过程中，由于数字串太长，不可避免地会发生数据录入错误。而通过校验位，能够大大减少数据录入错误。

J Verhoeff[2]基于对手工录入时发生的 12 000个错误的研究，将人们常犯的错误进行总结，共分为7类。⑴单个错误，a变成b，在所有错误中约占60%～95%。⑵遗漏或增加 1个数字，占所有错误的 10%～20%。⑶换位错误，ab变成ba，占所有错误的10%～20%。⑷双子错误，如aa变成bb，占所有错误的0.5%～1.5%。⑸跳跃转换，如acb变成bca，占所有错误的0.5%～1.5%。⑹跳跃双子错误，如aca变成bcb，发生率＜1%。⑺发音错误，如1a与a0，英文的13与30、14与40、15与50等，发生率约0.5%。

可以看出，人们在处理数字错误时，常犯的错误以一位为主。因此，考虑增加校验位，针对一位错误，设计相应的算法，成为校验位研究的主要内容。

2 常见校验位算法的优缺点

2.1 按位累加取模

常见的模（除数）为7、9、11、13等质数，因其每一位余数均与该模互质。按位累加取模，赋予校验位。在验证时，按同样算法进行比较，相等说明编码正确，不等则编码有误。

优点是算法简单，可以校验出大部分一位错误。缺点是累加取模，无位置信息，不能判断出相邻转换错误，如ab变成ba。当模的数字＜10时，会出现相关重复错误情况，导致不能检测出所有单个错误，如取模为 7 的7与0、8与1、9与2，取模为9的9与0等。

2.2 多项式乘法校验位算法

原理为 K元组的点乘和取余，即（a1，a2……ak）·(w1，w2……wk) mod m＝(a1w1＋a2w2＋……akwk) mod m＝0。常见的模m为10或11。

2.2.1 取模m为10 UPC编码（universal product code）是最早大规模应用的条码，为长度固定、连续性的条码，主要在美国和加拿大使用，由于其应用范围广泛，故又被称为万用条码。UPC编码仅可用来表示数字，故其字码集为数字0～9。在UPC编码中，a1、a2……a12满足以下等式：（a1，a2,……,a12）·（3，1，3，1……3，1） mod 10＝0，a12为校验位值。

优点是可以检测出所有的单个错误，也可以检测出ab变成ba这种相邻位置换位错误。缺点是不能检测出abc变成cba这种错误，也不能检测出|a-b|＝5的交换错误[3]。

2.2.2 取模m为11 模为11时，余数为0，1，2，3，4，5，6，7，8，9，10。当余数为10时，为了不增加位数，往往用X来代替。如国际图书编码ISBN 号0-669-19493，校验位X，代表10，校验位a10满足（a1，a2,……,a9，a10）·（10，9，8，7，6，5，4，3，2，1）mod 11＝0。

优点是可以检测出所有一位错误及相邻位置换位错误。缺点是增加了字母X，使编码不再是纯数字，在信息系统定义数据类型方面存在不便。由于在计算机表示中，数字的表示与字母的表示存在着差别，将两者合在一起来表示某一特定的编码，无疑增加了算法处理的复杂性，增加了系统设计及改造的成本，增加了系统处理的难度以及社会使用成本。

我国的身份证校验位算法即使用上述算法。根据中华人民共和国国家标准GB 11643－1999中有关公民身份号码的规定，公民身份号码是特征组合码，由17位数字本体码和1位数字校验码组成。排列顺序从左至右依次为6位数字地址码、8位数字出生日期码、3位数字顺序码和1位数字校验码。校验位根据前面17位数字码，按照ISO 7064:1983.MOD 11-2编码规则∑（ai×wi）mod 11计算。其中，i表示号码字符从右至左包括校验码在内的位置序号；ai表示第i位置上的号码字符值；wi表示第i位置上的加权因子，其数值依据公式是wi＝2（i－1）mod 11。

以某男性公民身份证号码为例，其本体码为34052419800101001，按照上述公式计算，见表1。

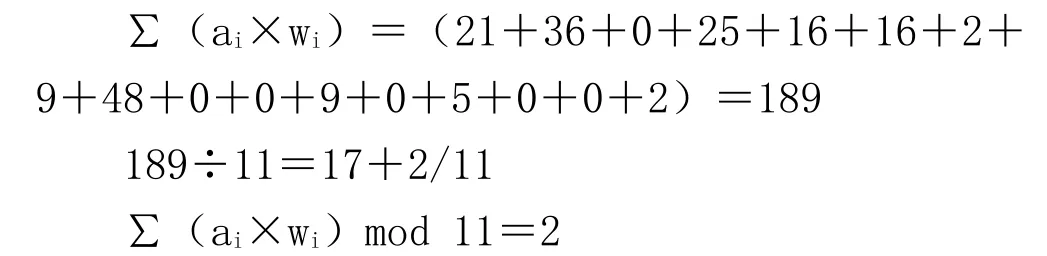
根据计算结果，从表2中查出，计算结果为2的校验码为 X，所以该男性公民身份证号码应该为34052419800101001X。

表1 某男性公民身份证校验位算法表

表2 身份证取模m为11的余数与校验码对照表

3 二面体群D5算法思想及其在SCTlD中的应用

法国天才数学家伽罗瓦于1822年首次提出“群”的概念，目的是解决高次方程有无定解以及解的表示问题。如一个正四边形，其旋转90°、180°、270°、360°，形状仍与原来的形状重合；而其左右对角线、水平及垂直平分线均反射对称。抽象出来，具有旋转对称与反射对称的正n边形，称为二面体。旋转与对称被称为二元运算中的元素。它的各种变换可以由置换群来表示，其相应的变换迭加后得到的元素仍在群中。群是抽象代数研究的最主要内容。这种不再以单纯的数字的加减，而以数据的结构为主要的研究内容，是抽象代数的一个本质特征。

二面体群 D5，以正五边形为例，考虑其旋转对称，将360°分为5份，则分别是72°、144°、216°、288°、360°（或 0°）。而对称变换，则以某一个顶点作垂直于顶点所对的边的垂直平分线。这时，会发生顶点相关位置的交换。

对此作Calay（凯莱）乘法表，0代表旋转0° 或360°，1代表旋转72°，2代表旋转144°，3代表旋转216°，4代表旋转288°，5代表以正五边形的顶点A作反射对称变换，6代表以正五边形的顶点B作反射对称变换，以此类推。表中的具体数值是某两个变换叠加的结果（两个元素相乘），在二面体群D5乘法表中（见表3），3与6的相乘，结果为9，表示正五边形的起始状态，经过旋转216°，再以A点作对称变换，其结果与起始位置直接作 E点对称变换，结果是一样的。如此则可以完全表示出二面体群D5的变化规律。其各种复杂的变化规律都是以上基础规律的迭加。因此，可以利用连续变换的方法，得出最终的一个状态。

J Verhoeff于1969年开发出了基于二面体群D5的校验位算法。考虑数字串a1a2……an-1，增加1位校验位an，满足an*σ（a1）*σ2（a2）*σ3（a3）*……σ（n-1）（an-1）＝0。这里σ2（x）＝σ(σ（x）)，σ3（x）＝σ(σ2（x）)。以此类推。由于如果 a≠b,σ有着σi（a）≠σi（b）。所有的单个数字错误均被检出。这里，σ代表某种置换，*代表二面体群D5乘法运算。二面体群D5乘法表见表3。

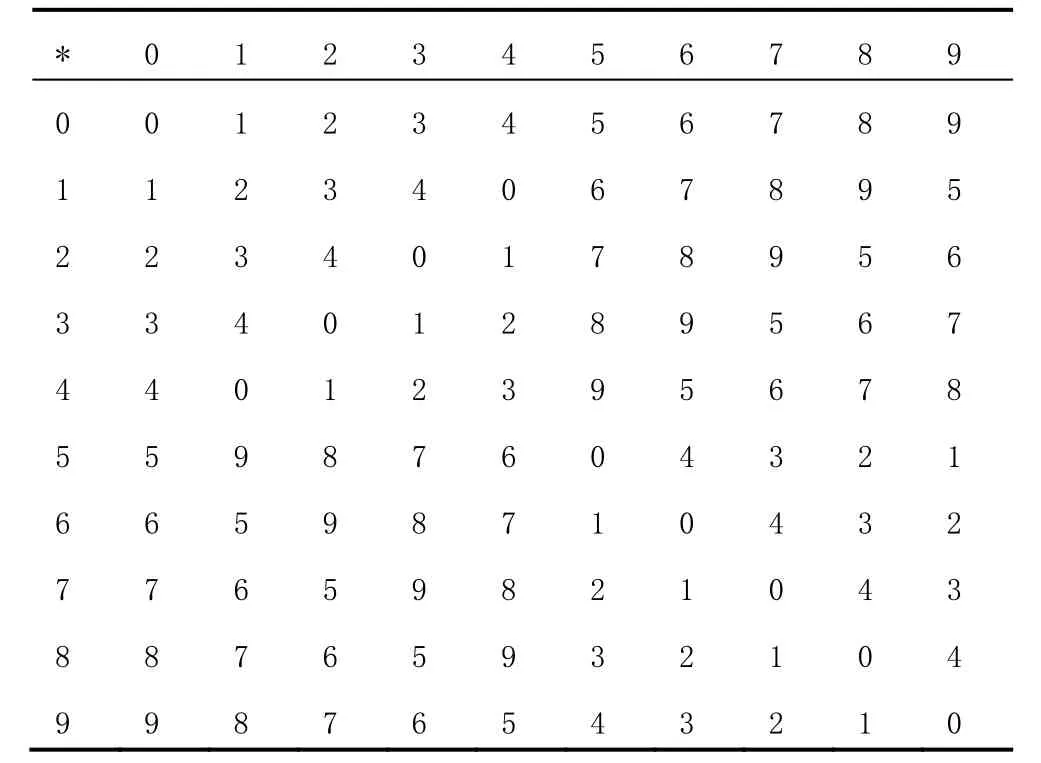
表3 二面体群D5乘法表

又由于，如果a≠b，a*σ（b）≠b*σ（a），可以推出σi（a）*σ（i＋1）（b）≠σi（b）*σ（i＋1）（a），因此，所有的包括相邻位置的交换错误均被检出。

表4为变换如σ=（01589427）（36）形成的置换表。

SNOMED CT中的SCTID，即采用了二面体群D5算法进行校验[4]。如 SNOMED CT（RF1）中的代码138875005，代表SNOMED CT Concept，其最后的“5”是校验位，是根据前面8个数字，通过二面体D5校验位算法得出的数值。

首先，设 a0为校验位，将数字串倒序排列为a000578831,依据等式：a0*σ1（0）*σ2（0）*σ3（5）*σ4（7）*σ5（8）*σ6（8）*σ7（3）*σ8（1）＝0

按照表4，得出a0*1*5*4*8*0*1*6*1=0

从右边开始计算，

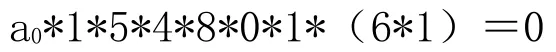
最后，产生完整的编码：138875005。

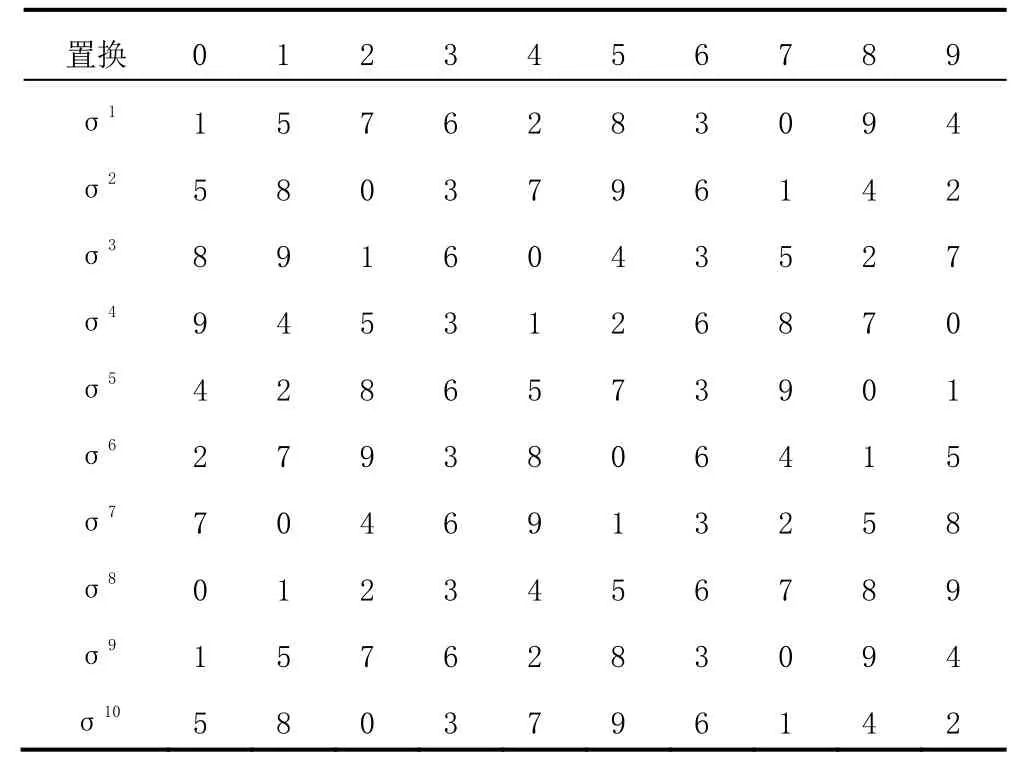
表4 置换表σ=（01589427）（36）

J Verhoeff的校验捕获了所有的单个错误、所有的相邻交换错误、＞95%的双子错误、＞94%的跳跃转换与跳跃双子错误，及大多数的元音错误。因此，与mod 11一样，减少校验错误至2%～3%，但是不需要增加X[5-6]。

4 对于中医术语编码的意义

编码的目的在于应用，在于方便地被计算机处理。通过校验位算法，不仅可以判断是否存在输入错误，也可以判断是否是有效的编码，从而提高实际应用的准确性。代码的准确性是代码应用的基础，而校验位对于代码录入准确性的提高，起到了重要的作用。从而使后续基于代码的若干应用成为可能。与条形码、二维码等结合起来，便捷地进行数据录入，可顺畅地实现信息化的各种流程。

在实际进行中医术语编码过程中，可以考虑按机构、分类、序号进行编码，通过算法产生完整编码并发布。而对于中医术语服务平台而言，可以提供编码服务、编码校验服务等相关功能[7]。

准确而统一的编码也是知识库构建的基础，知识库的构建依赖于无歧义的编码。如某一个诊断，可能是某几个症状的集合，体现为某一个编码可以分解为另外几个编码的集合。

曾有观点认为，中医本质上是术语，术语规范了，中医也就规范了。这句话可能不够全面，但是有着很深的道理。对于任何一门学科而言，都可以理解为本质上是数据，数据规范了，学科本身也就规范了。而对于计算机而言，更有意义的是基于术语的编码，以及编码与编码之间的关系。

纵观中医发展史，数学内容较少，这也是中医发展步伐较慢的根本原因。不能从相关数据中获取得到模型，不能进行有效的验证，不能摒弃错误或不正确的理论，发展就会缓慢，这主要是受当时的环境条件所限。但是，如今到了信息社会，网络高度发达，可以进行大规模的数据采集与分析，进行群体研究，从宏观疗效到微观机制更加深入地研究，这些为中医的现代化以及中医自身的进步与突破提供了可能。对于计算机而言，体现数据质量与效率之处，莫过于中医自身规范而统一的术语编码体系。

5 讨论

二面体群D5以其具有全反对称映射的10个数字最小组合，在数字编码中具有重要意义。而校验位的另一个重要作用是具有防伪功能，如信用卡号的3个校验位，以及部分国家的纸币编码。

目前，国内尚无一套既具有信息技术特征，又具有中医学科本身特征的医学术语集。而其中的编码，是中医术语集制定过程中的重要内容。二面体群 D5校验位算法，是SNOMED编码所采用的算法，对中医术语集体系结构的制定具有非常重要的借鉴意义。

但是，要对其进行深入研究，需要解决以下3个问题。

第一，σ=（01589427）（36）如何产生，有无其他的置换序列。回答这个问题，需要理解全反对称映射这个概念，即如果a≠b，a*σ（b）≠b*σ（a）。笔者通过设计相应算法，找到了34 040个全反对称映射，0～9这10个数字的全排列10!为3 628 800，34 040个全反对称映射占其 0.938%。如（01572）（496），（0284316）,(0519324678),(1932758)（46）等。这使得中医术语的编码可以不再局限于已有的SNOMED编码置换序列。

第二，如何产生出字母与数字组合的校验位算法。二面体群 D18可以解决英文字符与数字混合的校验位编码问题，但需要对其全反对称序列查找设计相应的算法。

第三，变换序列的分类以及校验准确度的评估问题。针对前文中提到的常犯的7类错误，需要对每一类变换能够解决各种错误的错误率进行分析。

而对于一位数字的纠错，可以采用两位校验位算法，不仅可以确定一位数字的录入错误，而且可以确定是哪一个位置发生错误，从而可自动纠正一位数字错误。这些问题，都是后续研究的重要内容。

[1] 成福春,刘华,房敏.基于 SNOMED术语编码两节点之间多路径算法的实现及其对中医术语编码的意义[J].中国中医药图书情报杂志,2014, 38(1):9-12.

[2] J Verhoeff. Error Detecting Decimal Codes[M]. Amsterdam: The Mathematical Center,1969.

[3] J A Gallian. The Mathematics of Identification Numbers[J]. The College Mathematics Journal,1991,22(3):194-202.

[4] International Health Terminology Standards Development Organization. SNOMED CT Technical Implementation Guide CVR 30363434[S]. Denmark: IHTSDO,2012.

[5] J A Gallian, S Winters. Modular Arithmetic in the Marketplace[J]. The American Mathematical Monthly,1988,95(6):548-551.

[6] Wagner, Putter. Error Detecting Decimal Digits[J]. CACM,1989, 32(1):106-110.

[7] 成福春,张平,刘华,等.中医术语集制定过程中关系的提炼及中医术语服务平台构建探讨[J].中国中医药图书情报杂志,2014,38(6):6-10.

Analysis on the Check-digit Algorithm of SNOMED and Its Significance to Traditional Chinese Medicine Terminology

CHENG Fu-chun1, ZHANG Ping2*, LIU Hua1, FANG Min1
(1. Yueyang Hospital of Integrated Traditional Chinese and Western Medicine, Shanghai University of Traditional Chinese Medicine, Shanghai 200437, China; 2. Shuguang Hospital Affiliated to Shanghai University of Traditional Chinese Medicine, Shanghai 201203, China)

This article discussed the advantages and disadvantages of commonly used check-digit algorithms, such as bitwise accumulation module and polynomial multiplication accumulation module. It attached importance to the SNOMED adopting dihedral group D5. Dihedral group D5can test all single bit mistakes and adjacent position bitwise mistakes without adding X, which is a very ideal check-digit algorithm. There does not exist a coding terminology set with the characteristics of information technology or TCM. SNOMED adopted dihedral group D5, which can provide references for TCM terminology coding.

TCM terminology; terminology coding; SNOMED; check-digit algorithm; dihedral group D5

10.3969/j.issn.2095-5707.2015.04.003

上海市卫生局科研计划课题（2009261）

成福春，副研究员，研究方向为中医信息学。E-mail: cfc1998cn@126.com

*通讯作者：张平，主治医师，研究方向为中医内科学。E-mail: zp1266@126.com

2015-01-05；编辑：魏民）